The effect of group polarization and its mathematical modeling

Introduction

A long time ago, an American psychologist J. Stoner conducted an interesting experiment (at a time when people could be so mocked with impunity). He took a group of students and each gave a questionnaire with (conditionally) dichotomous questions. After they answered, Stoner invited them to discuss these issues all together. And after discussion again to answer the same questions. To his great scientific success, the result was extremely interesting.

After a group discussion, the answers began to be more “risky” in nature. The word “risky” is, naturally, a kind of euphemism, which conceals the fact that people faced with a group of like-minded people with a group of ideological opponents have become a bit brutalized and have become more aggressive in defending their original views. This phenomenon is called "group polarization."



By naivety, scientists then (and many now) think that discussion helps to reach consensus. Not. Discussion of the dichotomy does not help to reach consensus, if it was not intended. Discussion helps the society to split into two camps that cannot tolerate each other. And with the advent of the Internet and endless Internet disputes over any occasion, this process has become even more ambitious .
')
But, however sad it may be, the social consequences of such a process and the endless polarizing cries of various fighters for the idea do not bother me very much. But the opportunity to model it with the help of mathematics interests me.

main idea

A society is generated where each member has his own dichotomous opinion on a particularly burning issue in the form of numbers from -1 to 1. For example, wear red pants or blue ones. For example, a person who corresponds to the figure -0.9 - loves red pants, and 0.9 - blue. A man with zero to his pants is indifferent and wears skirts.

In addition, each person has a level of defensive reactions, which prevents him from accepting new views and the desire to switch to individuals for any reason.

Once in an iteration, some kind of social act occurs. Conventionally - "People in blue pants went to the rally." Not all, but especially ideological. At the rally, each of them interacts with random people. He may agree with them or not, depending on how unanimous the interlocutor is with him and not inclined to become personal.
That's all.

After several iterations, it looks like how the distribution of love for different colors of pants in the population has changed.

Model Description

Modeled "society" of $$$M$individuals. Each individual has several characteristics:

$$$c$- cultural affiliation. Number from -1 to 1.
$$$d = c + N (0,0.4)$- level of defense reactions, “correlated” with $$$c$. The more you fit into the culture, the stronger the defensive reaction. $$$N (0.0.4)$- a random variable distributed normally with respect to 0 with a standard deviation of 0.4.
$$$a = U (0,1)$- Ad hominem rate. The desire for any reason to go to the individual. Naturally, the more it is, the less understanding with a person with whom you have different views. $$$U (0,1)$- uniform distribution from 0 to 1.

Constants:
$$$cs$- the basic step of changing the cultural context (love for the color of the pants).
$$$ds$- The basic step of changing the level of protection.

Iteration (public social act):
For random people with ideals who have $$$c> 0$, it checks how great the ideals are by comparing with a random number
If a $$$2c> rand (0,1)$, then the person interacts with [1: 6] random people from the entire sample. And so for everyone with inequality.
There may be questions - why $$$2c$, but not $$$c$. It may be that in the distribution of too few people with a sufficiently large ideology, therefore $$$c$multiplied by 2. But in general it can all be from $$$c$and not to depend.

Actually the interaction of people:
If people are of one mind
Naturally, they cannot quarrel on the issue, therefore success and failure are not checked for them. But they can assert themselves by agreeing with each other. Therefore, we first find how close they are in their unanimity. $$$\ Delta c = c_1-c_2$, and then:

If a $$$p = 1-e ^ {- 5 (1- \ Delta c) ^ 2}> rand (0,1) = r$then each of them:

$$

$$c = c + sign (c) \ cdot cs \ cdot | p-r |$$

$$

$$d = d + ds \ cdot | p-r |$$

Those. they believe more in their theory and their defenses for their theory are strengthened.

If people of different views
Then they have $$$\ Delta c = 0.5 (c_1-c_2)$, 0.5, so that the unit does not climb. And the probability of consent is considered as:

$$

$$p = (1-e ^ {- 5 (1- \ Delta c) ^ 2}) (1-a_1) (1-d_2).$$

Here $$$a_1$- the desire to pass on the identity of the participant interaction in your text, $$$d_2$- read defensive reaction. Naturally, a full transition to the individual guarantees 0 understanding, as well as too strong defensive reactions.

If the communication is successful and $$$p$more random $$$r$, then:

$$

$$c_1 = c_1 + sign (c_1) \ cdot cs \ cdot | p-r |,$$

$$

$$c_2 = c_2 + sign (c_1) \ cdot cs \ cdot | p-r |,$$

$$

$$d = d-ds \ cdot | p-r |.$$

Perceived shifts views towards the party. Both have defenses falling.

If the communication is unsuccessful and $$$p$less random $$$r$, then:

$$

$$c_2 = c_2-sign (c_1) \ cdot cs \ cdot | p-r |,$$

$$

$$d = d + ds \ cdot | p-r |.$$

The reader reads away from the participant and both have their defenses raised.
Meanings $$$c$and $$$d$- limited to maximum values, which are calculated from the initial sample.

Again, there may be questions about this calculation of the probability of an agreement, subject to the absence of defensive reactions and the transition to the individual: $$$(1-e ^ {- 5 (1- \ Delta c) ^ 2})$. But everything is simple $$$(1- \ Delta c) ^ 2$- a member that can not exceed 1. "5" is a coefficient that would be good to choose empirically, but in this case it is simply voluntarily appointed so that the process converges in a reasonable number of iterations.

Some scenarios when modeling

Neutral society

1000 people $$$c = N (0,2)$. 150 iterations.


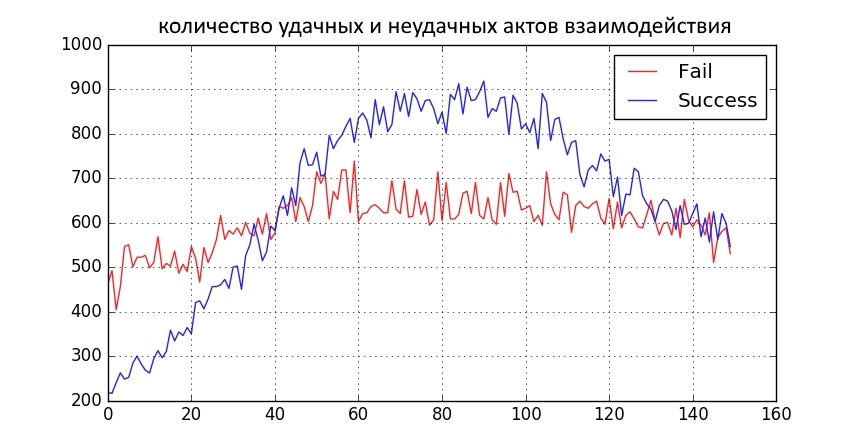
The top two graphs show how the type of distribution of views has changed over 150 iterations. On the x axis - the severity of views. On the y axis - the number of carriers of views (normalized). The lower graph shows the number of successful and unsuccessful acts of interaction with people of opposite views per iteration.

What can be seen on the charts?

1. The society was dichotomized.
2. The red part of the distribution "clung" to 0, but remained red. Those. It has become a lot of moderate lovers of red pants.
3. The “blue” part either went into a moderate minus (to the red), or crawled away into the “blue” radicalism.
4. The number of good interactions over the period increased, then decreased. This is predictable, because the blue ones are radicalized, and the red ones are red.
5. Due to radicalization, more people became involved in promotions. Then the blue part of the distribution began to blur and it became less involved.

Red Pants Society

1000 people $$$c = N (-1,2)$, 150 iterations.

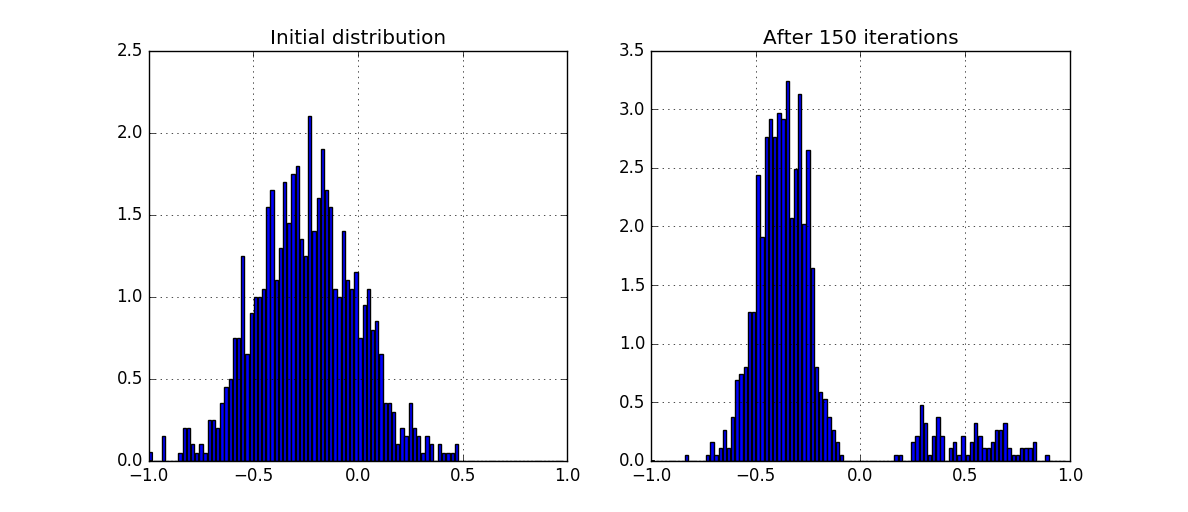
1. The society was dichotomized.
2. The “red part” did not “collapse” to 0, although it does not have such a strong tendency.
3. The blue part was smeared in approximately "uniform" distribution.
4. The number of both successful and not very communication has increased.

Dual society

500 people with $$$c = N (-2,2)$, 500 people with $$$c = N (2,2)$, 150 flash mobs.




The situation is close to the first, but immediately a large level of communication failures due to the great radicalism of both groups.

Neutral homogeneous society

1000 people with c = N (0,1). 150 iterations. Uniformity lies in the fact that the distribution is much narrower than in the first variant. Those. all people are very close in their initial pofigizm to the color of his pants. Just a bit do not care. A little bit.

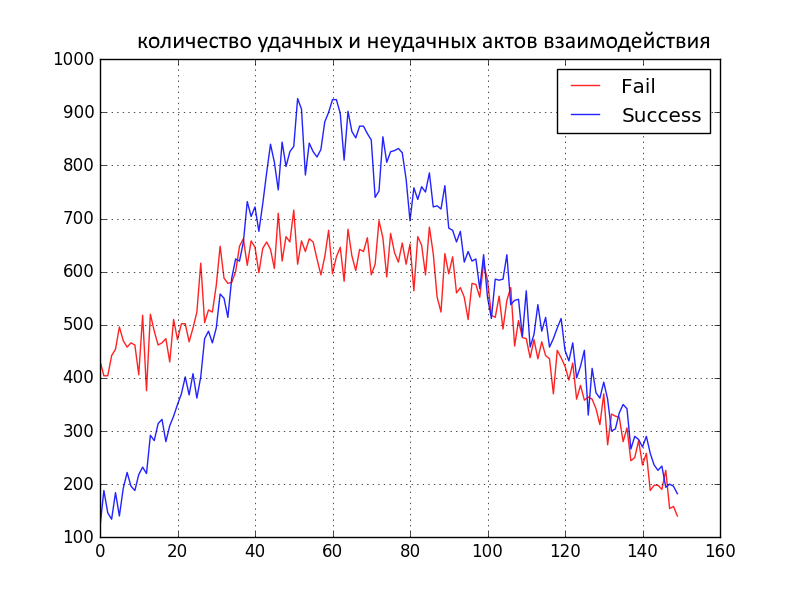
1. This is the only option when the blue pants "win" and the red ones remain in the minority. In many ways, this is due to a narrower initial distribution, due to the presence of which people are supposedly cursing less, because there is less radicalism in attitudes and defensive reactions. Smoothly indifferent to the color of the pants, the population is shifting towards the general acceptance of blue pants.
2. Positive and negative interactions go to 0, because for the interactions of people of the same views, these parameters are not considered.

Considerations on the limitations of the model

• It does not take into account that people are spinning in circles close to them, so for the most part they interact with their own. BUT. This only affects the ability to listen to the opposite point of view, so we can assume that there is a rather positive interaction in this model.
• It does not take into account that there are any opinion leaders who can apply directly to a large part of the sample.
• The active position is occupied only by the side of blue pants. Only she spends "shares". But it is like a feature by design, not a bug.
• The odds are somewhat from the ceiling, but where do you get them from? You can customize according to the original experiment or the results of the vote in some talk show. We'll see.

Mini output

Under this model, people still manage to negotiate on dichotomous issues. But only in the event that initially it is enough to give a damn to the question. This fits well with the qualitative description of the phenomenon, where “group polarization” does not occur when people are not interested or unfamiliar with the question. Moreover, it follows from the model that if people initially do not care about something, it is much easier for them to accept something as their own views. The thing is banal, it has never been applied in practice by deeply ideological thought leaders. Eternally, they should immediately begin to shout something loudly so that people immediately split into two teams.

Article author: Alexander Bespalov, Data Analyst, Maxilect