Algorithm Paccos. Understandable article on consensus in a distributed system
In this article, we will analyze the Paxos consensus algorithm, discuss why it is needed, why it works, prove its correctness and talk a little about the problems of practical application. In many ways, this is a free retelling of Leslie Lamport 's Paxos Made Simple article .
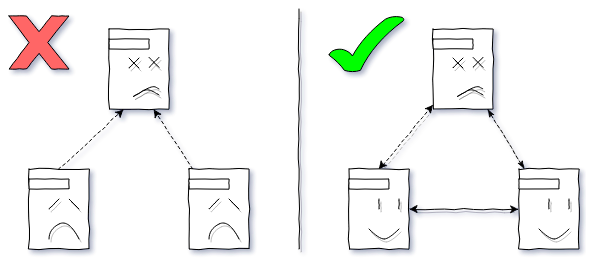
Often, when a distributed system is running (simply several servers processing user requests or distributed storage or something else like this), it is necessary to make general decisions, for example, on which server to start a singleton cluster-level service and where to migrate it when it drops server. This task is simply solved in the presence of the arbiter of the decision maker - the admin server. The problem is that the arbitrator becomes a single point of collapse, its failure may lead to a complete or partial system malfunction, and its restoration and restoration of the system’s performance will require manual intervention. Obviously, a fault-tolerant system should consist of equal participants able to agree among themselves on common issues - to reach a consensus. Usually, as a result of negotiations, an arbitrator is chosen (using the terms: leader, master) and further questions, while he is in good condition, are decided through him.
Leslie Lamport, originally wanted to prove mathematically rigorously that consensus in a distributed system with unreliable communications is impossible, but instead he invented and proved the Paxos (Paxos) algorithm that allows such a consensus to be reached. The description of the algorithm, which can be found, for example, in Wikipedia looks deceptively simple and short, but it is not easy to understand, and even more difficult to put into practice.
')
This algorithm has important limitations: it describes the process of choosing only one value, in practice, you need to make a lot of decisions, and for each subsequent case you will need to create a new instance of the algorithm. It is also assumed that the participants of the system behave not in Byzantine style, i.e. keep their promises, do not provide false data (I don’t know the story, but I feel - the Byzantines' reputation was so-self)
The concept of “choice” (choice of decision, choice of meaning) in the context of consensus algorithms differs from the everyday one. If in real life we compare the pros and cons, then in the case of a consensus algorithm, the choice is made from equivalent options, i.e. Any value / solution will do; the main thing is to decide which of the many proposed are specific.
This can be compared to how you three with friends come to the pizzeria, where the whole pizza is equally good (or bad) and try to choose which big pizza to order for three, the only waiter approaches you, and you continue to look puzzled in the menu. Because of the neighboring tables, they begin to suggest: “Take Pepperone already, do not delay, no worse than anything else” - this was the proposal (proposal) and the proposal was made by the proposer. One of you heard him and thinks: “OK, let it be pepperoni”. He is the acceptor and has just accepted the (to accept) offer . They shout from another table: “They are telling you for the third time - take Margarita and let them accept the order” - this is another proposal , and “you are the third time” is the proposal number (proposal number), and “Margarita” is value of the sentence . Then the waiter begins to ask you who took what offers. He is a recognizer (leaner) and if the majority (majority) of you accepted the same offer (“I’m telling you Margarita for the third time”) then this offer is called chosen , and if the majority tells it to the waiter, the waiter will know ( to learn) about the selected value and will be able to accept the order. But, let's say, one of those who accepted the third offer stuck in the smartphone and does not respond to the waiter's question.
The value was chosen, but it is impossible to recognize it - the two friends remaining in the real world give out contradictory answers. The next round of negotiations begins and perhaps a new proposal will be accepted, and the participant stuck in the smartphone will continue to read Habr. So, the correct algorithm of consensus sets such negotiation rules that any next selected value will coincide with the first selected value.
So we figured out the terminology and roles:
In practice, roles can and will be combined, for example, if we talk about servers choosing a leader between themselves, each server can offer itself as a leader, will accept offers (including its own offers), and in the end it needs to know who was chosen.
The majority means “more than half”, i.e. N + 1 from 2N + 1 (and from 2N too) or more.
The requirement of acceptance by the majority is obvious: if choosing a value would require acceptance by a smaller number of receivers (exactly half or less), then nothing would prevent to choose several different values at the same time, i.e. consensus would not have been reached. The fact that any two sets of the majority have a non-empty intersection will prove useful to us.
It does not require the participation of all the recipients in the selection, the other recipients may be faulty, communication with them may be broken. Thus, we get that the system of 2N + 1 participants is able to survive the failure of N of them.
We have already mentioned the offer number. Each proposal has a number. In the description of Lamport, this is a natural number such that:
The following analogy helped me to understand the algorithm: the number is essentially timestamp sentences, together timestamps set the global synthetic time of the distributed system designed so that a) no two sentences can be made (issued) at the same time , b) it is possible to understand which of the two proposals is made “later”. Accepting a proposal, it will ignore proposals that were made “before” accepted (sentences “from the past”).
In practice, the offer number will consist of a pair: the value of the offer counter of the specific server and the server identifier.
The value v is selected if the offer with number m and value v was accepted by the majority of recipients. After that, any subsequent selected value (accepted by the majority of the receivers) must match the selected v .
This requirement can be fulfilled if, after the value of v has been chosen, the recipients will only accept sentences with values equal to v .
The receiver accepts what the bidders offer and that means the previous requirement will be able to be fulfilled in turn if all the bidders in all the offers with the number n> m offer only the previously selected value v .
Let's imagine if we prove the last statement by induction and try to understand what is missing to make the induction transition.
In a strict mathematical language, this is formulated by Lamport as follows: to perform an induction step, it is necessary that the following invariant be fulfilled:
In order to ensure the existence of the above-described set S , the planner who plans to make an offer n must find out from the majority of the recipients what the number and value of the last sentence they will receive before n .
See what the problem is: the proposer may ask any recipient of the number and value of the last accepted offer, but there is a chance that having already sent the answer, the recipient will accept the next offer and the answer received by the proposer will be outdated and useless. To avoid this, Lamport came up with the following: let the proposer not only ask for the meaning of the last accepted proposal, but also ask not to accept any sentences with a number less than n . In response, the recipient will receive from the recipient: 1) the value and number of the last offer accepted by the recipient and 2) the promise not to accept any offers with numbers less than n . Then the information on the last accepted offer received in response will not become outdated, and if answers are received from the majority of the recipients, then these recipients form the desired set S. As soon as the set S is formed, the proposer makes an (n, v) clause ( where v , as we discussed above, is the value of the last sentence (the sentence with the maximum number) received by the recipient from the set S up to the moment n ).
Thus, we obtained the correct consensus algorithm, where the proposals are made in two stages:
To find out that a value has been chosen, the recognizer must see that the same sentence (number plus value) was accepted by the majority of the recipients.
The message exchange is asynchronous, the communications are unreliable, so it is not known whether the one who offers at least some answers will get it without waiting for the required number of promises the proposal will repeat the attempt by making the following sentence. All this can be repeated for a long time.
The algorithm does not guarantee that a consensus will be reached. Let's say that one offeror receives from the majority a promise not to accept offers with a number less than 1, the second one after him receives from the majority a promise not to accept offers with a number less than 2. That is, The 1st sentence can no longer be selected. Realizing that his offer will not be chosen, the first bidder will try to receive from the majority a promise not to accept offers with number less than 3. Now the 2nd offer cannot be accepted either. And so two proposing to infinity can incline the majority of the recipients to one side or the other, blocking the opportunity to reach consensus. This can be corrected by introducing random delays into the algorithm, and of course it is desirable to do so as soon as possible so that there is only one proposer. To do this, when it is necessary to make multiple decisions, when choosing the next value as a proposing one uses the leader selected in the previous step (in the previous instance of the algorithm).
But a new problem will arise: if we chose a leader, nothing prevents the remaining nodes behind him from initiating new elections and choosing another leader among themselves, they will succeed in collecting a quorum. In this case, the previous leader may not know anything about it and will continue to act considering that he is in charge here.
Another difficulty is dishonest Byzantine behavior and for this it is not necessary to have a malicious code among the elements of the system. For example, the recipients are obliged to remember their promise, for this they save it to disk, damage to the data on the disk (due to a failure or careless deletion of files by the operator) will lead to Byzantine behavior. In practice, even data in memory can be damaged with the same unfortunate result. Errors in the code can also cause Byzantine behavior.
You can read about these and other problems of the Paxos algorithm in the fascinating article by Google developers "Paxos Made Live - An Engineering Perspective" , where they talk about their experience in implementing distributed consensus in the Chubby project (internal Zookeeper analogue)
Thus, the Paxos algorithm is not a silver bullet, but only a small remarkable fundamental building block of our knowledge about fault-tolerant distributed systems.
Why you need distributed consensus and what it is

Often, when a distributed system is running (simply several servers processing user requests or distributed storage or something else like this), it is necessary to make general decisions, for example, on which server to start a singleton cluster-level service and where to migrate it when it drops server. This task is simply solved in the presence of the arbiter of the decision maker - the admin server. The problem is that the arbitrator becomes a single point of collapse, its failure may lead to a complete or partial system malfunction, and its restoration and restoration of the system’s performance will require manual intervention. Obviously, a fault-tolerant system should consist of equal participants able to agree among themselves on common issues - to reach a consensus. Usually, as a result of negotiations, an arbitrator is chosen (using the terms: leader, master) and further questions, while he is in good condition, are decided through him.
Leslie Lamport, originally wanted to prove mathematically rigorously that consensus in a distributed system with unreliable communications is impossible, but instead he invented and proved the Paxos (Paxos) algorithm that allows such a consensus to be reached. The description of the algorithm, which can be found, for example, in Wikipedia looks deceptively simple and short, but it is not easy to understand, and even more difficult to put into practice.
')
This algorithm has important limitations: it describes the process of choosing only one value, in practice, you need to make a lot of decisions, and for each subsequent case you will need to create a new instance of the algorithm. It is also assumed that the participants of the system behave not in Byzantine style, i.e. keep their promises, do not provide false data (I don’t know the story, but I feel - the Byzantines' reputation was so-self)
Choice and roles
The concept of “choice” (choice of decision, choice of meaning) in the context of consensus algorithms differs from the everyday one. If in real life we compare the pros and cons, then in the case of a consensus algorithm, the choice is made from equivalent options, i.e. Any value / solution will do; the main thing is to decide which of the many proposed are specific.
This can be compared to how you three with friends come to the pizzeria, where the whole pizza is equally good (or bad) and try to choose which big pizza to order for three, the only waiter approaches you, and you continue to look puzzled in the menu. Because of the neighboring tables, they begin to suggest: “Take Pepperone already, do not delay, no worse than anything else” - this was the proposal (proposal) and the proposal was made by the proposer. One of you heard him and thinks: “OK, let it be pepperoni”. He is the acceptor and has just accepted the (to accept) offer . They shout from another table: “They are telling you for the third time - take Margarita and let them accept the order” - this is another proposal , and “you are the third time” is the proposal number (proposal number), and “Margarita” is value of the sentence . Then the waiter begins to ask you who took what offers. He is a recognizer (leaner) and if the majority (majority) of you accepted the same offer (“I’m telling you Margarita for the third time”) then this offer is called chosen , and if the majority tells it to the waiter, the waiter will know ( to learn) about the selected value and will be able to accept the order. But, let's say, one of those who accepted the third offer stuck in the smartphone and does not respond to the waiter's question.
The value was chosen, but it is impossible to recognize it - the two friends remaining in the real world give out contradictory answers. The next round of negotiations begins and perhaps a new proposal will be accepted, and the participant stuck in the smartphone will continue to read Habr. So, the correct algorithm of consensus sets such negotiation rules that any next selected value will coincide with the first selected value.
Look again, this is a very important and absolutely wonderful moment: the state of the system (accepted values) is distributed among the nodes - each recipient knows only about the proposal he accepted, the general value was chosen, but a situation may arise when it is impossible to recognize it and even it was impossible to recognize whether something is selected. In this case, the negotiations will continue. But Paxos is such that any next selected by the majority of the receiving value will coincide with the first selected. The choice, once made, will not be changed.
So we figured out the terminology and roles:
- Offerors make offers .
- Receivers - accept offers, and remember the accepted ( number and value ). In this case, the receiver will accept the first incoming offer and will accept subsequent ones even if the choice has already been made.
- Finding out - find out what offer was chosen (accepted by the majority of participants).
In practice, roles can and will be combined, for example, if we talk about servers choosing a leader between themselves, each server can offer itself as a leader, will accept offers (including its own offers), and in the end it needs to know who was chosen.
About most
The majority means “more than half”, i.e. N + 1 from 2N + 1 (and from 2N too) or more.
The requirement of acceptance by the majority is obvious: if choosing a value would require acceptance by a smaller number of receivers (exactly half or less), then nothing would prevent to choose several different values at the same time, i.e. consensus would not have been reached. The fact that any two sets of the majority have a non-empty intersection will prove useful to us.
It does not require the participation of all the recipients in the selection, the other recipients may be faulty, communication with them may be broken. Thus, we get that the system of 2N + 1 participants is able to survive the failure of N of them.
Global time distributed system
We have already mentioned the offer number. Each proposal has a number. In the description of Lamport, this is a natural number such that:
- the number is unique, it has its own in each sentence;
- the bidder uses a larger number for each subsequent sentence.
The following analogy helped me to understand the algorithm: the number is essentially timestamp sentences, together timestamps set the global synthetic time of the distributed system designed so that a) no two sentences can be made (issued) at the same time , b) it is possible to understand which of the two proposals is made “later”. Accepting a proposal, it will ignore proposals that were made “before” accepted (sentences “from the past”).
In practice, the offer number will consist of a pair: the value of the offer counter of the specific server and the server identifier.
We construct the correct algorithm
The value v is selected if the offer with number m and value v was accepted by the majority of recipients. After that, any subsequent selected value (accepted by the majority of the receivers) must match the selected v .
This requirement can be fulfilled if, after the value of v has been chosen, the recipients will only accept sentences with values equal to v .
The receiver accepts what the bidders offer and that means the previous requirement will be able to be fulfilled in turn if all the bidders in all the offers with the number n> m offer only the previously selected value v .
Let's imagine if we prove the last statement by induction and try to understand what is missing to make the induction transition.
Sentence (m, v) - was chosen, i.e. there are many Cs consisting of the majority of the recipients and each of these recipients accepted the sentence (m, v) . It also follows from the induction hypothesis that all sentences with numbers from the range from m to n-1 inclusively have the value v (*). Now it is required to make so that the sentence with number n also had value v .
Suppose that there is a set S consisting of the majority of recipients and such that we can find out the value of the last sentence (with the maximum number less than n ) received by the recipient of this set. For example, the number of this “maximum” sentence is k . Since the set S contains at least one accepting a from the set C , then the number k will be greater than or equal to the number of the last received sentence, accept a , and the number of the last sentence of received a will be greater than or equal to number m (the moment the value was selected). . k> = m , and thus, by (*), the value of the sentence k is the previously chosen v , we will use it to generate the sentence (n, v) . Thus, if we are able to guarantee the existence of sets S , then this will provide an induction step.
In a strict mathematical language, this is formulated by Lamport as follows: to perform an induction step, it is necessary that the following invariant be fulfilled:
For any v and n , if the sentence (n, v) is made (issued), then there is a set S consisting of the majority of the receivers and such that one of two things is true: (a) no one accepting from the set S accepted any sentences with a number less than n or (b) v is the value of the sentence with the highest number less than n among all the offers accepted by the host from the set S.
In order to ensure the existence of the above-described set S , the planner who plans to make an offer n must find out from the majority of the recipients what the number and value of the last sentence they will receive before n .
See what the problem is: the proposer may ask any recipient of the number and value of the last accepted offer, but there is a chance that having already sent the answer, the recipient will accept the next offer and the answer received by the proposer will be outdated and useless. To avoid this, Lamport came up with the following: let the proposer not only ask for the meaning of the last accepted proposal, but also ask not to accept any sentences with a number less than n . In response, the recipient will receive from the recipient: 1) the value and number of the last offer accepted by the recipient and 2) the promise not to accept any offers with numbers less than n . Then the information on the last accepted offer received in response will not become outdated, and if answers are received from the majority of the recipients, then these recipients form the desired set S. As soon as the set S is formed, the proposer makes an (n, v) clause ( where v , as we discussed above, is the value of the last sentence (the sentence with the maximum number) received by the recipient from the set S up to the moment n ).
Thus, we obtained the correct consensus algorithm, where the proposals are made in two stages:
- Preparatory stage:
- Proposer sends an announcement that he plans to make an offer n (at time n )
- The recipients who receive the announcement send in response a promise not to accept any offers with numbers less than n (up to the moment n ), and also the last accepted offer (number and value) or do not answer at all if the number of the last received by the receiving offer exceeds n or if n is in proposals that the receiver has already promised not to accept another bidder.
- Sentence:
- The bidder, receiving answers from most of the recipients, chooses the value of the sentence v from the answer with the maximum number of the sentence and sends the sentence (n, v) .
- The receiver, having received the sentence (n, v) , is obliged to accept it if he, of course, did not promise the other bidder not to accept sentences with numbers less than n * , where n *> n .
To find out that a value has been chosen, the recognizer must see that the same sentence (number plus value) was accepted by the majority of the recipients.
Problems of practical application
The message exchange is asynchronous, the communications are unreliable, so it is not known whether the one who offers at least some answers will get it without waiting for the required number of promises the proposal will repeat the attempt by making the following sentence. All this can be repeated for a long time.
The algorithm does not guarantee that a consensus will be reached. Let's say that one offeror receives from the majority a promise not to accept offers with a number less than 1, the second one after him receives from the majority a promise not to accept offers with a number less than 2. That is, The 1st sentence can no longer be selected. Realizing that his offer will not be chosen, the first bidder will try to receive from the majority a promise not to accept offers with number less than 3. Now the 2nd offer cannot be accepted either. And so two proposing to infinity can incline the majority of the recipients to one side or the other, blocking the opportunity to reach consensus. This can be corrected by introducing random delays into the algorithm, and of course it is desirable to do so as soon as possible so that there is only one proposer. To do this, when it is necessary to make multiple decisions, when choosing the next value as a proposing one uses the leader selected in the previous step (in the previous instance of the algorithm).
But a new problem will arise: if we chose a leader, nothing prevents the remaining nodes behind him from initiating new elections and choosing another leader among themselves, they will succeed in collecting a quorum. In this case, the previous leader may not know anything about it and will continue to act considering that he is in charge here.
Another difficulty is dishonest Byzantine behavior and for this it is not necessary to have a malicious code among the elements of the system. For example, the recipients are obliged to remember their promise, for this they save it to disk, damage to the data on the disk (due to a failure or careless deletion of files by the operator) will lead to Byzantine behavior. In practice, even data in memory can be damaged with the same unfortunate result. Errors in the code can also cause Byzantine behavior.
You can read about these and other problems of the Paxos algorithm in the fascinating article by Google developers "Paxos Made Live - An Engineering Perspective" , where they talk about their experience in implementing distributed consensus in the Chubby project (internal Zookeeper analogue)
Thus, the Paxos algorithm is not a silver bullet, but only a small remarkable fundamental building block of our knowledge about fault-tolerant distributed systems.
Source: https://habr.com/ru/post/346180/
All Articles