Genetic algorithm for constructing algorithms

In a typical implementation, the genetic algorithm operates with parameters of some complex function (Diophantine equations in the article " Genetic algorithm. Just about complex " mrk-andreev ) or algorithm (" Evolution of racing cars in JavaScript " ilya42 ). The number of parameters is invariable, operations on them are also impossible to change, as genetics does not try, because they are given by us.

Houston, we have a problem

A strange situation has arisen - before applying genetic algorithms (GA) to a real problem, we must first find an algorithm by which this problem is solved in principle, and only then can it be optimized using a genetic algorithm. If we make a mistake with the choice of the “main” algorithm, then genetics will not find the optimum and will not say what the error is.

Often, and recently, it is fashionable to use a neural network instead of a deterministic algorithm. Here we also have the widest choice (FNN, CNN, RNN, LTSM, ...), but the problem remains the same - you need to choose the right one. According to Wikipedia, " Choose the type of network should be based on the formulation of the problem and the available data for training ."
')
What if...? If you force the GA not to optimize the parameters, but create another algorithm that is most suitable for this task. That's what I did for the sake of interest.

Genotype from operations

Let me remind you that genetic algorithms usually operate so-called. "Genotype" vector "genes". For the GA itself, it does not matter what these genes will be — numbers, letters, strings, or amino acids. It is only important to observe the necessary actions on genotypes - crossing, mutation, selection - not necessarily in this order.

So, the idea is that the “genome” will be an elementary operation, and the “genotype” will be an algorithm composed of these operations. For example, a genotype composed of mathematical operations and implementing the function

f (x) = e^{(f r a c 3 x + 20 0.34)^{2}}

$f (x) = e ^ {(\ frac {3x + 20} {0.34}) ^ 2}$ :

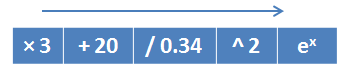
x3 | +20 | /0.34 | ^ 2 | e ^ x

Then, as a result of performing GA, we will get a formula or algorithm, the structure of which we cannot predict in advance.

Crossing does not actually change, the new genotype receives pieces from each parent.

A mutation can be the replacement of one of the genes for some other, that is, one operation is replaced in the algorithm and / or the parameters of this operation are changed.

With the selection and simple and difficult at the same time. Since we are creating an algorithm, the easiest way to check it is to execute it and evaluate the result obtained. So cars with their progress on the highway proved the optimality of its architecture. But the machines had a clear criterion - the further she traveled, the better. Our target algorithm in the general case can have several evaluation criteria — length (the shorter the better), memory requirements (the smaller the better), resistance to input garbage, etc.

By the way, the machines had one criterion, but it worked only within the current route. The best machine for one track would hardly be the best for another.

And if you think?

In the process of thinking about which operations to include in the gene dictionary and how they should work, I realized that I could not limit myself to operations on one variable. The same neural networks operate with all (FNN) or several (CNN) input variables at the same time, so you need a way to use the required number of variables in the resulting algorithm. And in what operation which variable is required, I cannot foresee and I do not want to limit.

I came to the rescue ... you can not guess ... the language of Forth . More precisely, the reverse Polish notation and stack machine with their ability to put variable values on the stack and perform operations on them in the right order. And without brackets.

For the stack machine, in addition to arithmetic operations, you need to program the stack operations - push (take the next value from the input stream and put it on the stack), pop (take the value from the stack and return it as a result), dup (duplicate the top value on the stack).

Just do it!

It turned out such an object that implements one gene.

Gen Object

class Gen(): func = 0 param = () def __init__(self): super().__init__() self.func = random.randint(0,7) self.param = round(random.random()*2-1,2) def calc(self, value, mem): if self.func == 0: # push mem.append(value + self.param) return (None, 1) elif self.func == 1: # pop return (mem.pop() + self.param, 0) elif self.func == 2: # dup mem.append(mem[-1] + self.param) return (None, 0) elif self.func == 3: # add mem.append(mem.pop() + value + self.param) return (None, 1) elif self.func == 4: # del mem.append(mem.pop() - (value + self.param)) return (None, 1) elif self.func == 5: # mul mem.append(mem.pop() * (value + self.param)) return (None, 1) elif self.func == 6: # div mem.append(mem.pop() / (value + self.param)) return (None, 1) return (self.params, 0) def funcName(self, func): if self.func >= 0 and self.func <= 7: return [ 'push', 'pop', 'dup', 'add', 'del', 'mul', 'div', 'const'][func] return str(func) def __str__(self): return "%s:%s" % (self.funcName(self.func), str(self.param))

It was the first option, in principle, working, but a problem quickly emerged with it - for arithmetic operations it was required to transmit a value, but not for pop and dup operations on the stack. I didn’t want to distinguish the called operations in the calling code and determine how many parameters should be passed to each of them, so I did it - instead of one value, I passed an array of input values, and let the operation itself do what it wants with it.

Gen v.2 object

 class Gen(): func = 0 param = () def __init__(self): super().__init__() self.func = random.randint(0,7) self.param = round(random.random()*2-1,2) def calc(self, values, mem): if self.func == 0: # pop return mem.pop() + self.param elif self.func == 1: # push mem.append(values.pop() + self.param) return None elif self.func == 2: # dup mem.append(mem[-1] + self.param) return None elif self.func == 3: # add mem.append(mem.pop() + values.pop() + self.param) return None elif self.func == 4: # del mem.append(mem.pop() - (values.pop() + self.param)) return None elif self.func == 5: # mul mem.append(mem.pop() * (values.pop() + self.param)) return None elif self.func == 6: # div mem.append(mem.pop() / (values.pop() + self.param)) return None return self.param def funcName(self, func): if self.func >= 0 and self.func <= 7: return [ 'pop', 'push', 'dup', 'add', 'del', 'mul', 'div', 'const'][func] return str(func) def __str__(self): return "%s:%s" % (self.funcName(self.func), str(self.param))

The second problem was that arithmetic operations were too demanding - they needed both the value on the stack and the input value. As a result, not a single genotype could form a genetic algorithm. It was necessary to divide the operations into those working with the stack and those working with the input value.

Below is the latest version.

Gen v.8 object

 class Gen(): func = 0 param = () def __init__(self, func=None): super().__init__() if func is None: funcMap = [0,1,2,3,4,5,6,7,8,9,10,11] i = random.randint(0,len(funcMap)-1) func = funcMap[i] self.func = func self.param = round((random.random()-0.5)*10,2) def calc(self, values, mem): def getVal(): v = values[0] values[0:1]=[] return v if self.func == 0: # pop return mem.pop() elif self.func == 1: # push mem.append(getVal()) return None elif self.func == 2: # dup mem.append(mem[-1] + self.param) return None elif self.func == 3: # addVal mem.append(getVal() + self.param) return None elif self.func == 4: # delVal mem.append(getVal() + self.param) return None elif self.func == 5: # mulVal mem.append(getVal() * self.param) return None elif self.func == 6: # divVal mem.append(getVal() / self.param) return None elif self.func == 7: # addMem mem.append(self.param + mem.pop()) return None elif self.func == 8: # delMem mem.append(self.param - mem.pop()) return None elif self.func == 9: # mulMem mem.append(self.param * mem.pop()) return None elif self.func == 10: # divMem mem.append(self.param / mem.pop()) return None mem.append(self.param) return None def funcName(self, func): funcNames = ( 'pop', 'push', 'dup', 'addVal', 'delVal', 'mulVal', 'divVal', 'addMem', 'delMem', 'mulMem', 'divMem', 'const') if self.func >= 0 and self.func < len(funcNames): return funcNames[func] return str(func) def __str__(self): return "%s:%s" % (self.funcName(self.func), str(round(self.param,4)))

I had to tinker a bit with the genotype object, selecting the crossing algorithm. Which one is better, I did not decide, I left pseudo-randomness at will. The algorithm itself was defined in the multiplication method __mul__ .

Dnk object

 class Dnk: gen = [] level = 0 def __init__(self, genlen=10): super().__init__() self.gen = [ Gen(1), Gen(1) ] + [ Gen() for i in range(genlen-2) ] def copy(self, src): self.gen = src.gen def __mul__(self, other): divider = 2 def sel(): v = random.random()*(self.level + other.level) return v <=self.level mode = random.randint(0,3) minLen = min(len(self.gen), len(other.gen)) maxLen = max(len(self.gen), len(other.gen)) n = Dnk() if mode == 0: n.gen = [ self.gen[i] if sel() else other.gen[i] for i in range(minLen) ] elif mode == 1: n.gen = [ Gen() for i in range(minLen) ] for g in n.gen: g.param += round((random.random()-0.5)/divider,3) elif mode == 2: n.gen = [ self.gen[i-1] if i % 2 == 1 else other.gen[i] for i in range(minLen) ] for g in n.gen: g.param += round((random.random()-0.5)/divider,3) else: v = random.randint(0,1) n.gen = [ self.gen[i] if i % 2 == v else other.gen[-1-i] for i in range(minLen) ] for g in n.gen: g.param += round((random.random()-0.5)/divider,3) n.gen = n.gen + [ Gen() for i in range(minLen,maxLen) ] return n def calc(self, values): res = [] mem = [] varr = values.copy() i = 0 for g in self.gen: try: r = g.calc(varr, mem) i = i + 1 except: self.gen = self.gen[0:i] #raise break; if not r is None: res.append(r) return res def __str__(self): return '(' + ', '.join([ str(g) for g in self.gen ]) + '):'+str(round(self.level,2))

For both classes, the method __str__ has been redefined to display their contents in the console.

The algorithm calculation function is a bit more detailed:

  def calc(self, values): res = [] mem = [] varr = values.copy() i = 0 for g in self.gen: try: r = g.calc(varr, mem) i = i + 1 except: self.gen = self.gen[0:i] #raise break; if not r is None: res.append(r) return res

Pay attention to the commented raise - initially I had an idea that a genotype with an algorithm flying out by mistake should not live in this world and should be rejected immediately. But there were too many mistakes, the population degenerated, and then I decided not to destroy the object, but to amputate it on this gene. So the genotype gets shorter, but remains working, and its working genes can be used.

So, there is a genotype, there is a dictionary of genes, there is a function of crossing two genotypes. You can check:

 >>> a = Dnk() >>> b = Dnk() >>> c = a * b >>> print(a) (push:4.061, push:1.79, dup:-4.32, mulMem:3.6, push:-3.752, addVal:2.4, delVal:-1.863, delMem:4.06, delVal:-3.692, addMem:0.48):0 >>> print(b) (push:0.356, push:-4.8, pop:2.865, delVal:1.53, addMem:-2.853, mulVal:-1.6, const:-2.451, delVal:-2.53, divVal:4.424, delMem:-0.6):0 >>> print(c) (push:4.061, divVal:4.424, dup:-4.32, const:-2.451, push:-3.752, addMem:-2.853, delVal:-1.863, pop:2.865, delVal:-3.692, push:0.356):0 >>>

Now we need breeding functions (selection and crossing the best) and mutations.
The functions of crossing and reproduction of genotypes to the required number I wrote in three versions. But the worst half dies anyway.

 #        def mixIts(its, needCount): half = needCount // 2 its[half:needCount] = [] nIts = [] l = min(len(its), half) ll = l // 2 for ii in range(half,needCount): i0 = random.randint(0,l-1) i1 = random.randint(0,l-1) d0 = its[i0] d1 = its[i1] nd = d0 * d1 mutate(nd) its.append(nd) #           def mixIts2(its, needCount): half = needCount // 2 its[half:needCount] = [] nIts = [] l = min(len(its), half) ll = l // 2 for ii in range(half,needCount): i0 = random.randint(0,ll-1) i1 = random.randint(ll,l-1) d0 = its[i0] d1 = its[i1] nd = d0 * d1 mutate(nd) its.append(nd) #            def mixIts3(its, needCount): half = needCount // 2 its[half:needCount] = [] nIts = [] l = min(len(its), half) ll = l // 4 for ii in range(half,needCount): i0 = random.randint(0,ll-1) i1 = random.randint(ll,ll*2-1) d0 = its[i0] d1 = its[i1] nd = d0 * d1 mutate(nd) its.append(nd)

The mutation function is applied to the new genotype.

 def mutate(it): #      listMix = [ (random.randint(0,len(it.gen)-1), random.randint(0,len(it.gen)-1)) for i in range(3) ] for i in listMix: it.gen[i[0]], it.gen[i[1]] = (it.gen[i[1]], it.gen[i[0]]) #    , for i in [ random.randint(0,len(it.gen)-1) for i in range(3) ]: it.gen[i] = Gen() #        for i in [ random.randint(0,len(it.gen)-1) for i in range(1) ]: it.gen[i].param = it.gen[i].param + (random.random()-0.5)*2

How can such a genetic algorithm be applied?
For example:
- identify patterns among the input data, regression analysis
- develop an algorithm that restores the fallout in the signal and removes interference - useful for voice communication
- to separate signals that came from different sources on the same channel - useful for voice control, creating a pseudo stereo

For these tasks, a genotype is needed, which will take as input an array of input values and produce an array of output values of the same length. I tried to combine the tasks of obtaining suitable genotypes and achieving the goal, it turned out to be too difficult. It was easier to get rid of genetics in order to select genotypes for the initial population, so that these genotypes could generally process the input array.

For the selection of genotypes, a function is written, it generates genotypes, drives them away from the GA, rejects the result and returns an array of survivors. HA terminates prematurely if the population has degenerated.

 #       dataLen = 6 #   itCount = 100 #    genLen = 80 #    epochCount = 100 srcData = [ i+1 for i in range(dataLen) ] def getIts(dest = 0): its = [ Dnk(genLen) for i in range(itCount) ] res = [] for epoch in range(epochCount): nIts = [] maxAchiev = 0 for it in its: try: res = it.calc(srcData) achiev = len(res) if achiev == 0: it = None continue maxAchiev = max(maxAchiev, achiev) it.level = achiev nIts.append(it) except: # print('Died',it[0],sys.exc_info()[1]) it = None its = nIts l = len(its) if l<2: print("Low it's count:",l) break; #  ,     its.sort(key = lambda it: -it.level) if maxAchiev >= dataLen: break; mixIts(its, itCount) for it in its[:]: if it.level<dest: its.remove(it) return its

The function of assessing the deviation of the result from the desired one (not quite a fitness function, because the greater the deviation, the worse the genotype, but we take this into account).

 def diffData(resData, srcData): #     ,       if len(resData) != len(srcData): return None d = 0 for i in range(len(resData)): d = d + abs((len(resData)*30 - i) * (resData[i] - srcData[i])) return d

Well, the final touch - actually the GA on the selected genotypes.

 #   bestCount = 30 #    globCount = 30000 #  ,        seekValue = 8000 its = [] while len(its)<bestCount: its = its + getIts(len(destData)) print('Its len', len(its)) # ,     printIts(its[0:1], srcData) its[bestCount:len(its)]=[] for glob in range(globCount): minD = None for it in its[:]: resData = it.calc(srcData) d = diffData(resData, destData) #    ,    . if d is None: its.remove(it) continue #        it.level = 100000 - d minD = d if minD is None else min(d, minD) its.sort(key = lambda it: -it.level) if glob % 100 == 0 or glob == globCount - 1: #   ,    100-  print('glob', glob, ':', round(minD,3) if minD else 'None', len(its)) #, resData) if minD < seekValue: print('Break') break mixIts2(its, bestCount) #     printIts(its[0:3], srcData)

Result

 ... glob 2900 : 7067.129 18 glob 3000 : 4789.967 15 glob 3100 : 6791.239 17 glob 3200 : 6809.478 15 Break 16 0 (const:24.7735, addMem:1.7929, dup:39.1318, dup:-15.2363, mulVal:24.952, mulVal:4.7857, pop:14.4176, pop:19.8343, dup:-19.4728, pop:2.6658, dup:-14.8237, pop:6.7005, pop:1.3567, pop:-2.7399):97009.88 => [9.571, 24.952, 30.989, 35.638, 50.462, 65.698] 1 (const:24.7735, dup:-4.8988, dup:39.1318, dup:-4.3082, mulVal:24.952, mulVal:6.1096, pop:14.4176, pop:19.8343, dup:-19.4728, pop:2.6658, dup:-14.8237, pop:6.7005, pop:1.3567, pop:-2.7128):96761.03 => [12.219, 24.952, 35.226, 39.875, 54.698, 59.007] 2 (const:24.7735, addMem:1.7929, dup:39.1318, dup:-15.2363, mulVal:24.952, delVal:3.4959, pop:14.4176, pop:19.8343, dup:-19.4728, pop:2.6658, dup:-14.8237, pop:6.7005, pop:1.3567, pop:-2.7399):96276.27 => [5.496, 24.952, 30.989, 35.638, 50.462, 65.698] >>>

Or, to put it simply, the best GA result with the goal of destData = [10, 20, 30, 40, 50, 60] was [9.571, 24.952, 30.989, 35.638, 50.462, 65.698]. This result is achieved by a genotype with an algorithm (const: 24.7735, addMem: 1.7929, dup: 39.1318, dup: -15.2363, mulVal: 24.952, mulVal: 4.7857, pop: 14.4176, pop: 19.8343, dup: -19.4728, pop: 2.6658, dup : -14.8237, pop: 6.7005, pop: 1.3567, pop: -2.7399).

On the one hand, the algorithm is redundant - it makes actions unnecessary to get the final result. On the other - the algorithm is limited, since it uses only two values from the input stream of six - it is clear that this happened because of the limited input data.

What's next?

You can further develop the idea:
- Run the resulting algorithm on a large data stream, and the further the algorithm “passes” along this stream with the minimum deviation, the better it is, the genotype is better. Complete analogy with cars.
- Include a full Forth-machine and make the generation of the algorithm in the text Forth. So you can create more complex algorithms for computing, with conditional transitions and cycles.
- Analyze and simplify the resulting algorithm so that only the most necessary for getting the result remains in it.
- Instead of elementary gene operations, use more complex ones. For example, such an operation may be differentiation. Or integration. Or learning neural network. Although Alan J. Perlis said that it was necessary not to inflate the dictionary, but to accumulate idioms, a good dictionary of idioms would not hurt.

Source: https://habr.com/ru/post/346134/

All Articles