Little about arithmetic

Have you ever thought about how we think? How is the score at a low level? For example, look like on a straight line segments in the expression 1 + 1 = 2 . Or what is the square root of $$$i$ .

The bill appeared not just to count, but to count some objects. For example, the number of apples or antelope in the herd. That is, there is always a unit of measurement.

You can read on fingers or sticks, that is, to set some correspondence between units of measurement. One antelope - one wand. Since any other units can be replaced with sticks, we will consider only them. A wand is an abstract unit of measurement.

Simple actions

It should be noted that the account is in ascending order. Such a counting stick itself implies the presence of the next stick. That is, the unit has a direction. So this is a single vector.
')
Adding one unit vector to the end of the other, we will move along the number line, getting new values.

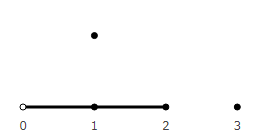
And then there are 4 options.



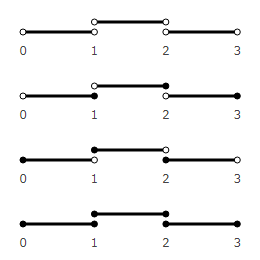
What do the ends of a unit segment look like? Which option best simulates a real account?

The first does not fit. Moving in this way, we never get into an integer. It seems to have counted to 1, but it does not belong to the first or second vector.

The fourth is also not suitable. If we are at point 1, then it is not clear whether this is the first vector or the second. When we count sheep that jump over a fence, they have no common points.

The second one looks the most correct. Reached point 1 - then counted 1 object. Each point belongs to one vector. We will use it in the future.

The third one also looks appropriate. But he has a peculiarity - point 0 belongs to the first vector. When there is nothing yet, we believe that something is already there. This is not like a real account. But it looks like an account used in computers. The first 32-bit cell in RAM occupies bytes with addresses 0, 1, 2, 3. To make it look like an account of real objects, it would be necessary to count from the address 1 * 4 and take bytes with an offset of 0, -1, -2, -3.

So the second option.



Please note, zero is not here. If you simply count in order, it is not entirely obvious that the point of reference is not the first unit, but something before it. Perhaps that is why zero appeared after the appearance of the actual account.

The result of the addition can be represented as a single vector from the initial point to the final one.

How to make a subtraction? For this you need to add to the consideration of the vector directed in the opposite direction.



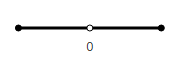
We assume that the shaded point means an arrow, that is, it shows the direction of the vector.

To distinguish these vectors, we will call them, respectively, positive and negative.

You can enter a direction change operation. After applying it to a positive vector, it turns out negative. After applying it 2 times, the original vector is obtained. In another way it can be called "unary minus" or "change of sign."

Negative vectors also form a sequence.



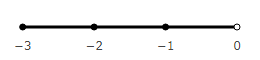
If we considered only the negative direction, we could use the same numbers as for the positive, that is, without a sign. But we consider both, and it is necessary to distinguish the counts in a positive and negative direction. Therefore, the numbers in the negative direction is a minus sign. Positive numbers can also be labeled with a plus sign, but this is not necessary, the difference is already there.



What does this mean? What is positive and negative 0. Geometrically, they are at one point. This binds the positive and negative beam of the counting direction.

Zero can be drawn shaded, but for this it is necessary to introduce a special vector of zero length, to which add ones. It can be obtained from unit vectors.

3 + -3 = 0


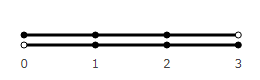
Technically, his left edge is also not included, but the right edge is at the same point. That is, a vector turns into a point, or otherwise, a point is a special case of a vector.

An interesting point, we can go to zero on the left or on the right. Accordingly, the sign he will be positive or negative. Something similar is mentioned here .

Since the point 0 is a vector of zero length, then we can say that the point taken separately on a straight line is 1, or 2, or 3, it is also a vector of zero length. It turns out that there are zero vectors that are connected by nonzero. This solves the question of why a segment of nonzero length consists of an infinite number of points of zero length. Because the points are always connected by nonzero vectors. These are the two opposites that form the system. Like 0 and 1 in binary number system.

With multiplication, everything is simple - we take the entire second vector as many times as the units in the first vector.

With the division more difficult. Just as subtraction is addition with change of sign, so division is multiplication by reverse number. That is, you must specify the method of obtaining the vector 1 / N. Since it is less than the unit vector, you need to enter a smaller unit of measurement.

For example, how to divide a vector with a length of 12 into 10 parts? We introduce a new vector of some length and set the condition that this vector, repeated 10 times, gives the original unit vector. As a result, we again obtain the calculations in integers. We divide 120 small vectors into 10 parts, we get 12 small ones or 1.2 units.



How to express the number pi through such vectors? No An exact expression in units means an exact decimal notation. Similarly, they cannot express the number $$$\ frac {1} {3}$ = 0.333 (3) . Otherwise, it will be necessary to enter infinitely smaller units to infinity. You can only denote these numbers in another way - by letter or expression.
Number $$$\ frac {1} {2}$ = 0.5 can be expressed, but only because the basis of our number system is a multiple of this number. In the decimal system, all fractions are periodic, except for those whose denominators are multiples of 2 or 5. This may not be entirely obvious, since we often work with finite fractions

We go beyond the boundaries

How to get to this point?



Moving only in a straight line, we can not get into it. So, it is necessary to introduce another unit vector perpendicular to the first one. Enter a positive and negative direction, determine the rules of addition and subtraction between all types of vectors. It turns out too hard. Many entities and set rules, moreover, similar to each other.

What if to approach from the other side? What needs to be done to get to a point away from the main direction? It is necessary to turn.



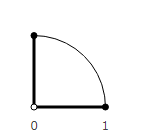
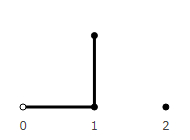
Rotated one vector and add up with another.

It is easy to see that turning a positive unit vector 2 times gives a negative vector.



Nothing like? But this is multiplication by an imaginary unit.

So what happens? $$$i$ it is not a vector perpendicular to the real direction. $$$i$ This is a right angle rotation. This is not a unit of direction, but a unit of rotation. Multiply vector by $$$i$ means turning the vector on $$$\ frac {\ pi} {2}$ through complex space. Sign change is a turn 2 times.

"Complex space" means that if we consider a two-dimensional graph of the function $$$y = f (x)$ , the imaginary part $$$x$ is in a plane perpendicular to the surface of the graph. To display it, you will need the third dimension, and the imaginary part $$$y$ will require the fourth. For a one-dimensional numerical line, the second is sufficient.

And what is the square root of $$$i$ ? Apparently this is such a value that multiplying a unit vector by 2 times gives a vector $$$1 \ cdot i$ .
Times multiplied by $$$i$ this is a turnaround $$$\ frac {\ pi} {2}$ , then multiplication by the root of $$$i$ this is a turnaround $$$\ frac {\ pi} {4}$ .

Check in Wolfram Alpha.




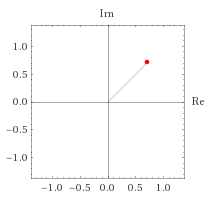
Yeah, it is.

Any kind expression $$$a + bi$ can be represented as $$$r \ cdot i ^ c$ where $$$r$ this is the length of the vector, and $$$c$ sets the rotation angle as a coefficient for $$$\ frac {\ pi} {2}$ .

$$$1 + 1i = 1.414 \ cdot i ^ {\ frac {1} {2}}$


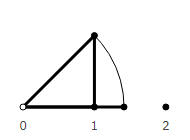
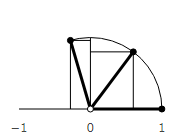
When multiplying numbers, the lengths are multiplied, and the corners are added together.

$$

$$\ begin {aligned} (0.6 + 0.8i) \ cdot (0.6 + 0.8i) = (0.36 + 0.48i + 0.48i - 0.64) = -0.28 + 0.96i \\ \ end {aligned}$$

$$

$$\ begin {aligned} 0.6 + 0.8i & = 1 \ cdot i ^ {\ frac {\ arcsin (0.8)} {\ frac {\ pi} {2}}} \\ & = 1 \ cdot i ^ {0.590334 ...} \\ (1 \ cdot i ^ {0.590334 ...}) \ cdot (1 \ cdot i ^ {0.590334 ...}) & = 1 \ cdot i ^ {0.590334 ... + 0.590334 .. .} \\ & = 1 \ cdot i ^ {1.180669 ...} \\ {1.180669 ...} \ cdot \ frac {\ pi} {2} & = {1.854590 ...} \\ sin (1.854590. ..) & = 0.96 \ cos (1.854590 ...) & = -0.28 \ end {aligned}$$

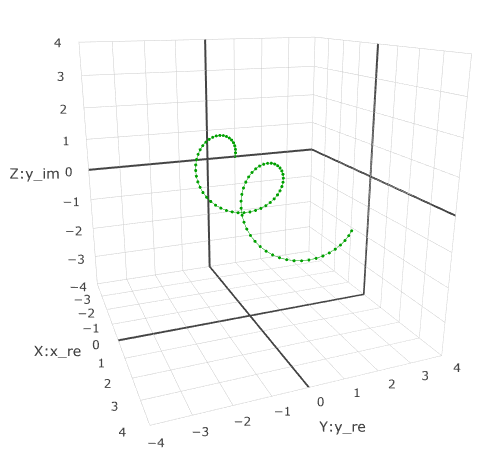
4 multiplications on i return the vector to its original state. Multiplication graph by $$$i$ with a change in the degree of 0.1, gives the usual unit circle. If you expand it along the axis $$$x$ , we get the usual sine and cosine. What do you think the sine and cosine look like in 3D? This is a spiral.

$$$y = i ^ x$






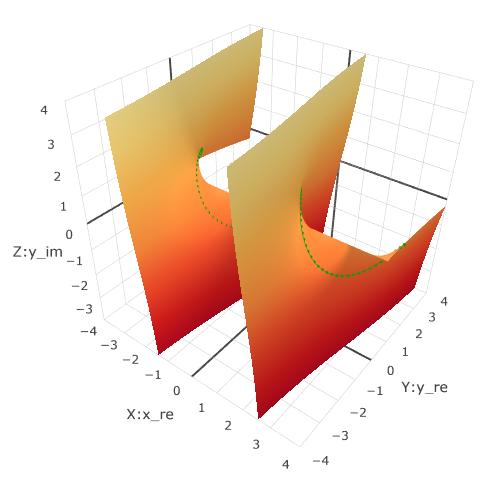
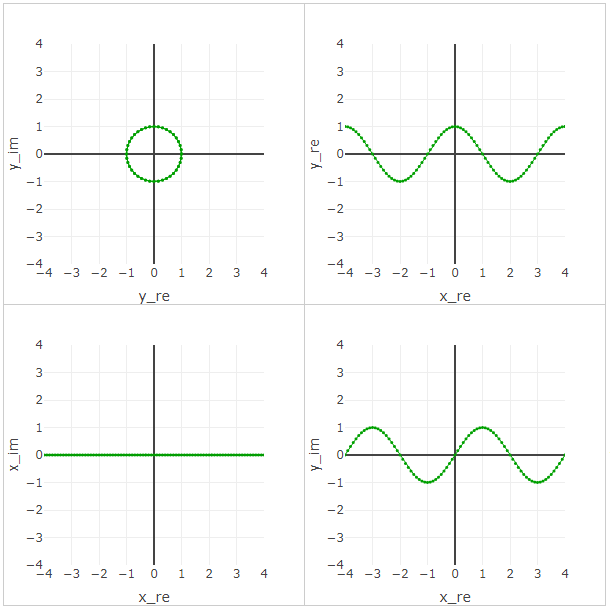
Here the period is integer, since $$$x$ The turns are counted, not the circumference.

The pictures are clickable, the links are an interactive page with graphs. In the “Axis mappping” block it is determined which 3 of the 4 axes are shown in 3D. In the “Function 1” and “Function 2” fields there is a javascript code from which an object of the type Function is created.
In URL hash, in base64 hash, in base64 json, in json field values.
Signatures are not related to the central axes, but to the lines along which the numbers are laid.
Calculations in complex numbers are performed using math.js , graphs are made using plotly.js .

What if not multiply by $$$i$ and on $$$1.1i$ ? Instead of a circle, you will get a divergent logarithmic spiral .





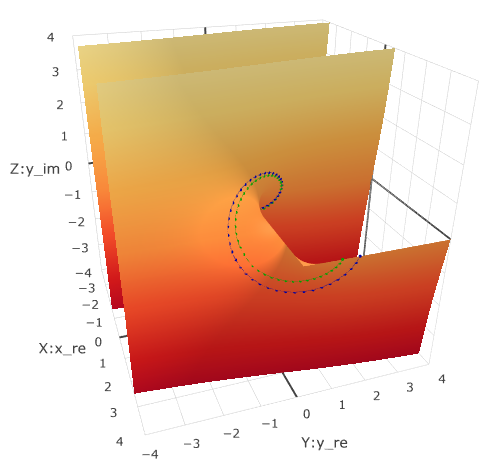
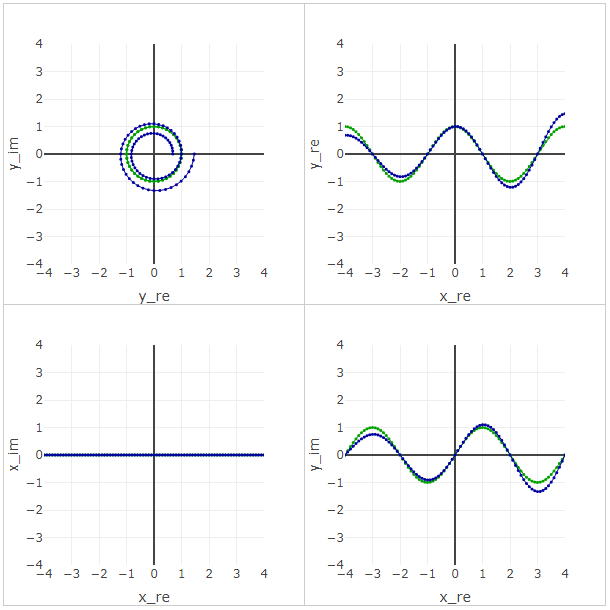
Let us return briefly to the division. The reverse number is a power of -1. This is due to the movement along this logarithmic spiral.

This is the function graph. $$$y = (2i) ^ x, \, x = -1..1$ . The length of the vector varies from $$$\ frac {1} {2}$ up to 2.



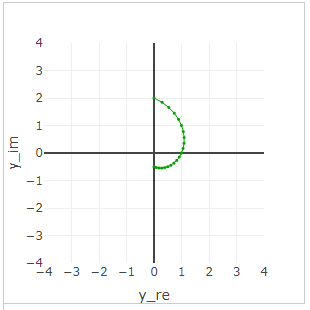
The radius length plot is a regular exponential graph of the form. $$$a ^ x$ .

A special case

Consider the function graph $$$e ^ x$




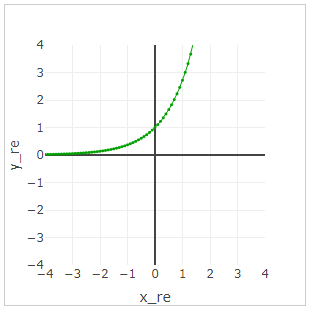
Euler's identity looks like this:
$$$e ^ {i \ pi} + 1 = 0$

This is a special case of the Euler formula. What does it mean?
It means that the value of the function $$$e ^ x$ in the real point $$$x = 0$ with imaginary part $$$\ pi$ equals -1.

Add a function graph $$$e ^ {ix}$ .



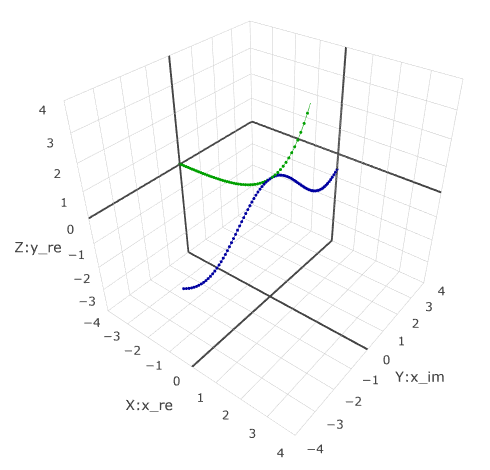
It goes perpendicular to the material and looks like $$$\ cos (x)$ . therefore $$$e ^ {- i \ pi}$ , $$$e ^ {3i \ pi}$ , $$$e ^ {- 3i \ pi}$ are also -1.

The picture that is drawn in Wikipedia , you can get it . The value for the Y axis in Axis mapping is different.

In a three-dimensional view, a wavy surface is obtained.






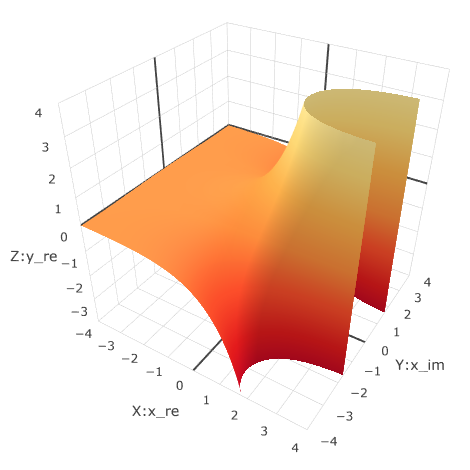
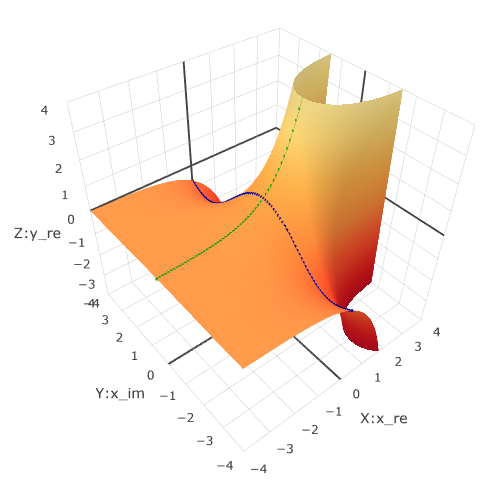
To get the latest graph, you need to additionally run the buildFuncSurface() function in the console. In the interface, you can only set 2 series of points, and at the last of them there are 3. To manage the series, there are functions addTraces()/deleteTraces() .

There is also an altform() function that shows the record of a complex number in the form $$$r \ cdot i ^ c$

 console.log(altform(math.i.sqrt())) 0.707106781187 + 0.707106781187i = 1 * i^0.5 = 1 * i^(1/2) 

There are also Plotly and math objects that are added by libraries.