About the shape of a rotating fluid

Today, I made tea for myself and thought

This morning, I thought, while stirring two cubes of sugar in a cup with just brewed tea. I thought about the shape of the fluid that it takes during the rotation. Of course, everyone imagines what will happen if you very quickly start stirring sugar in a cup of tea. I wanted to consider this banal and familiar process in more detail and try to tell you some interesting things about the physics of the phenomena surrounding us in everyday life.

The idea of ​​the experiment

Let's imagine that we have some cylindrical container in which there is some liquid. The liquid can be rotated in at least two obvious ways: stir it with some object or start rotating the cylindrical container, which, due to the friction forces between the liquid and the surface of the vessel, will result in the rotation of the liquid carried by the rotating vessels containing it.

Physical model

Let's stop on the second variant. So, we have a vessel rotating at a constant cyclic frequency, in which, under dynamic equilibrium with a constant cyclic frequency, the fluid rotates in the same direction.

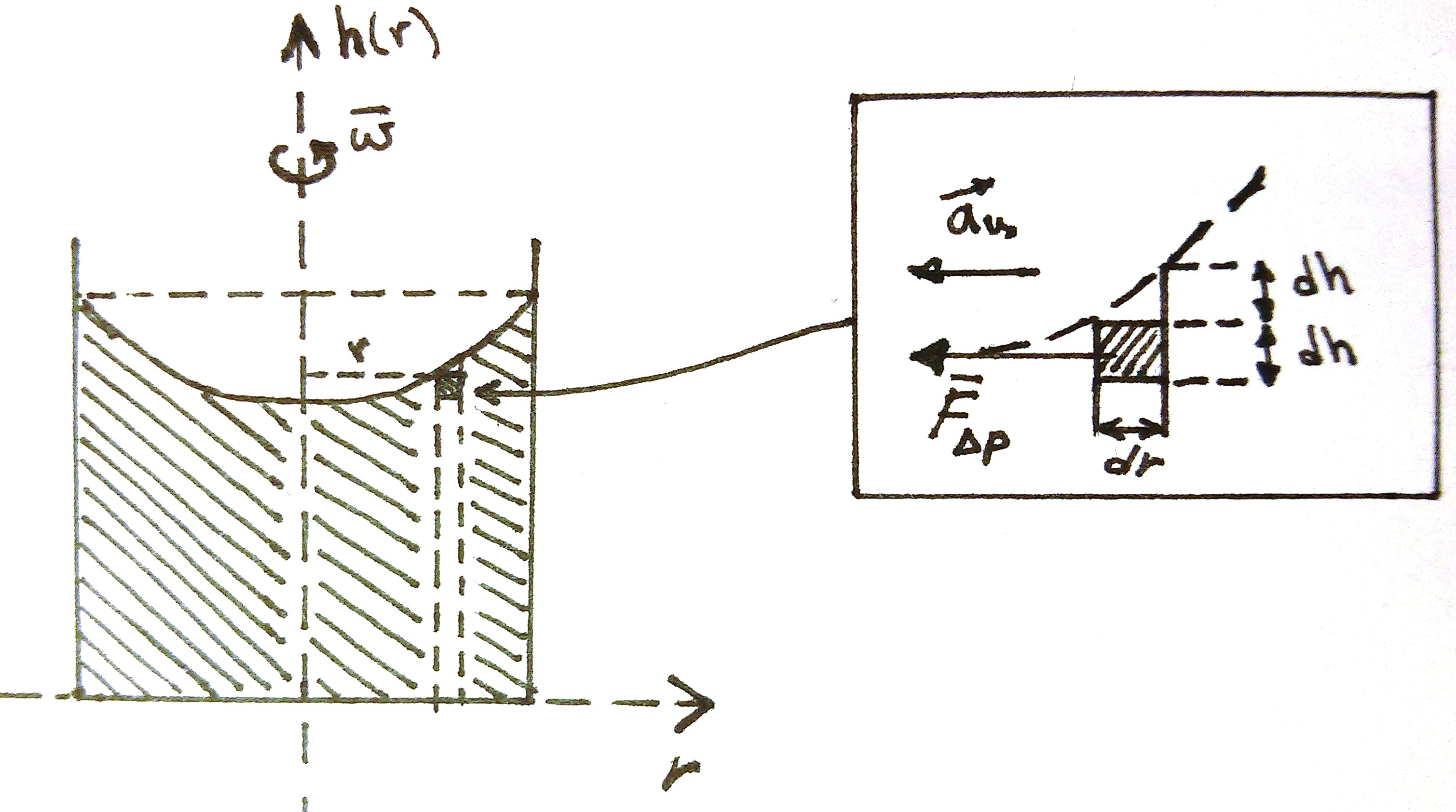
Let's cut out from the whole liquid an elementary infinitely small volume near the surface and consider what forces act on it. Due to the symmetry of the problem, we will be guided by cylindrical coordinates, which will significantly simplify the calculations.

Qualitative calculation of the surface shape

We write Newton's second law for an elementary piece of the volume of a liquid:
$$$m \ overrightarrow a = \ sum \ limits_i {\ overrightarrow F _i}$
For example, after stirring with a spoon of sugar in a cup of freshly brewed tea, the liquid rotates around the axis of symmetry, hence our elementary piece of volume has a centripetal acceleration. Therefore, we project our Newton's law onto an axis that coincides with the radius vector from the elementary volume to the axis of symmetry. We will not take into account the viscosity and surface tension. The force imparting centripetal acceleration (on the right side of our law of motion) will arise due to the pressure difference between the pillars of the liquid, which can be seen in the enlarged part of the first figure.
')
Thus, we get the following expression:
$$$Or: ma_ {c} = F _ {\ Delta p}$ where $$$a_ {c} = \ frac {{v ^ 2}} {r} = \ frac {{\ left ({\ omega r} \ right) ^ 2}} {r} = \ omega ^ 2 r$ , and that very force will be defined as $$$F _ {\ Delta p} = \ Delta p \ cdot S_ {eff.section}$ where area of ​​effective section $$$S_ {eff.section} = rd \ varphi \ cdot dh = rd \ varphi dh$ denotes the area of ​​our elemental volume, which is affected by the pressure difference of the liquid columns $$$\ Delta p = \ rho gdh$ .
Get power $$$F _ {\ Delta p} = \ rho gdh \ cdot rd \ varphi dh = \ rho grd \ varphi \ left ({dh} \ right) ^ 2$

The mass of our volume element is determined by the familiar formula. $$$m = \ rho dV$ and the volume itself will be equal to $$$dV = rd \ varphi \ cdot dh \ cdot dr$ (elementary volume in cylindrical coordinates).
As a result, Newton's 2 law for our little problem is signed in the following expression:
$$$\ rho rd \ varphi \ cdot dh \ cdot dr \ cdot \ omega ^ 2 r = \ rho grd \ varphi \ left ({dh} \ right) ^ 2$
After small reductions and transformations we get:
$$$\ omega ^ 2 rdr = gdh$
Now we integrate both sides of the expression using indefinite integrals:
$$$\ int {\ omega ^ 2 rdr = \ int {gdh}}$
$$$\ omega ^ 2 \ frac {{r ^ 2}} {2} = gh + const$
$$$h (r) = \ frac {{\ omega ^ 2}} {{2g}} r ^ 2 + C$

Detailed calculation of the surface shape

Now we have a very clear relationship for the shape of the surface and we can confidently say that this is a paraboloid. But we do not know the constant value. $$$C$ . Let's define it to fully understand the physics of the process.

Since the volume of liquid does not change (we believe that we did not spill a drop while we were stirring our tea ツ), then we will write down the volumes before rotation and during rotation with a constant cyclic frequency.

Before rotation:
$$$V = \ pi R ^ 2 H$ where $$$H$ - this is the height of the liquid in the cylindrical surface in a calm state (no rotation).

During rotation:
$$$V = \ int {\ int {\ int {dV}}} = \ int {\ int {\ int {rd \ varphi dhdr}}}$
$$$\ begin {array} {l} V = \ int \ limits_0 ^ {2 \ pi} {d \ varphi} \ int \ limits_0 ^ R {rdr} \ int \ limits_0 ^ {\ frac {{\ omega ^ 2} } {{2g}} r ^ 2 + C} {dh} = \ int \ limits_0 ^ {2 \ pi} {d \ varphi} \ int \ limits_0 ^ R {r \ left ({\ frac {{\ omega ^ 2}} {{2g}} r ^ 2 + C} \ right) dr} = \ int \ limits_0 ^ {2 \ pi} {d \ varphi} \ int \ limits_0 ^ R {\ left ({\ frac {{ \ omega ^ 2}} {{2g}} r ^ 3 + Cr} \ right) dr} = \\ = \ int \ limits_0 ^ {2 \ pi} {\ left ({\ frac {{\ omega ^ 2} } {{8g}} R ^ 4 + \ frac {C} {2} R ^ 2} \ right) d \ varphi} = \ left ({\ frac {{\ omega ^ 2}} {{8g}} R ^ 4 + \ frac {C} {2} R ^ 2} \ right) 2 \ pi = \ frac {{\ pi \ omega ^ 2}} {{4g}} R ^ 4 + \ pi CR ^ 2 \\ \ end {array}$

These volumes are equal, therefore:
$$$\ pi R ^ 2 H = \ frac {{\ pi \ omega ^ 2}} {{4g}} R ^ 4 + \ pi CR ^ 2$
Hence the previously unknown constant is expressed: $$$C = \ frac {1} {{R ^ 2}} \ left [{R ^ 2 H - \ frac {{\ omega ^ 2}} {{4g}} R ^ 4} \ right] = H - \ frac {{\ omega ^ 2}} {{4g}} R ^ 2$
And the final equation of the shape of the surface of a rotating fluid is:
$$$h (r) = \ frac {{\ omega ^ 2}} {{2g}} r ^ 2 + H - \ frac {{\ omega ^ 2}} {{4g}} R ^ 2$ or transforming $$$h (r) = \ frac {{\ omega ^ 2}} {{2g}} \ left ({r ^ 2 - \ frac {{R ^ 2}} {2}} \ right) + H$

Some notes

I would like to draw attention to the fact that the shape of the surface depends on the frequency of rotation, the acceleration of gravity, the geometrical parameters of the vessel, the initial volume of the liquid, but does not depend on the density of the liquid. This expression seemed to me quite interesting, since with its help one can easily simulate the approximate location of the liquid inside a cylindrical vessel rotating around its axis of symmetry. To do this, you can use MathCAD and build several graphs.

Graphic representation of the calculation results

Take the very real parameters of the system, commensurate with the size of a cup or cup.
Cylindrical surface radius: $$$R0: = 0.05$
The height of the liquid in a cylindrical surface without rotation: $$$H0: = 0.1$
Acceleration of gravity: $$$g0: = 9.81$
Cyclic rotational speed of the cylindrical surface: $$$w0$
(All values ​​of these values ​​are given in the C system)

Next, we rewrite our function to display it in MathCAD.
For 2D section display:
$$$h (r): = if \ left ({- R0 \ le r \ le R0, \ frac {{w0 ^ 2}} {{2 \ cdot g0}} \ cdot \ left ({r ^ 2 - \ frac {{R0 ^ 2}} {2}} \ right) + H0,0} \ right)$

For 3D surface mapping:
$$$N0: = 100$
$$$i: = 0..N0$
$$$j: = 0..N0$
$$$x_i: = 0.001 \ cdot \ left ({2 \ cdot i - N0} \ right)$
$$$y_j: = 0.001 \ cdot \ left ({2 \ cdot j - N0} \ right)$
$$$r (x, y): = \ sqrt {x ^ 2 + y ^ 2}$
$$$hv (x, y): = \ frac {{w0 ^ 2}} {{2 \ cdot g0}} \ cdot \ left ({r ^ 2 (x, y) - \ frac {{R0 ^ 2}} {2}} \ right) + H0$
$$$fh (x, y): = if \ left ({- R0 \ le r (x, y) \ le R0, if (hv (x, y) \ ge 0, hv (x, y), 0), 0} \ right)$
$$$M_ {i, j}: = fh (x_i, y_j)$

As a variable parameter, we will change the cyclic frequency of rotation. $$$w0$ . The results can be seen in the figures below:


At cyclic frequency $$$w0 = 0 (rad / c)$


At cyclic frequency $$$w0 = 5 (rad / c)$


At cyclic frequency $$$w0 = 15 (rad / c)$


At cyclic frequency $$$w0 = 25 (rad / c)$


At cyclic frequency $$$w0 = 39.5 (rad / c)$


At cyclic frequency $$$w0 = 90 (rad / s)$

findings

It can be seen that if the cyclic frequency exceeds the value $$$w0 = 39.5 (rad / c)$ then we will see the bottom of a rotating cylindrical vessel, and, starting from this frequency, the liquid will smoothly “pass” onto the vessel walls, increasingly exposing the bottom. It is obvious that at very high frequencies all the liquid will spread along the walls of the vessel. Now we know all the parameters of such a liquid. Knowing its equation, it will not be difficult to calculate the thickness of the liquid layer on the vessel wall at a certain height at a certain frequency.

upd. Separately, I would like to emphasize those contradictory assumptions that were taken when considering the problem:
1. It was believed that the liquid rotates due to the rotation of the vessel that contains it. This can only be when taking into account internal friction, viscosity and surface tension.
2. But in deriving the surface shape, these phenomena are not taken into account in order to simplify the solution and show only qualitative simulation results. Those. The decision contradicts the model described initially. Accounting for all phenomena, including the non-linearity of the process at high frequencies, would complicate the task so much that it could hardly be solved analytically and show an approximate and understandable model for a person who is not associated with mathematics / physics.
3. The goal was to show only a very approximate and simplest solution, which includes a number of assumptions.