TAU for the smallest: an example of the implementation of the PID controller in Unity3D

Instead of introducing

Automatic control systems (ACS) are designed to automatically change one or more parameters of the control object in order to establish the required mode of its operation. The ACS maintains the constancy of the specified values of the controlled parameters or changes them according to a given law, or optimizes certain control quality criteria. For example, such systems include:

stabilization systems
program management systems
tracking systems

This is a fairly wide class of systems that can be found anywhere. But what does this have to do with Unity3D and probably with games in particular? In principle, the direct one: in any game, SAUs are implemented using simulation as an element of gameplay, such games include, for example, Kerbal Space Programm, Digital Combat Simulator (formerly Lock On), Strike Suit Zero , etc. (who knows more examples - write in the comments). In principle, any game that simulates real physical processes, including just kinematics with driving dynamics, can implement certain ACSs - this approach is simpler, more natural, and the developer already has a set of ready-made tools provided by all sorts of Vyshnegradsky, Lyapunovy, Kalmans , Chebyshev and other Kolomogorov, so you can do without the invention of the bicycle, because it has already been invented, so much so that a separate science has turned out: The theory of automatic control. The main thing here is not to overdo it. One thing is only a problem: they don't talk about TAU everywhere, not everyone, often a little and not very clear.

Little theory

The classic automatic control system presented in the following figure:

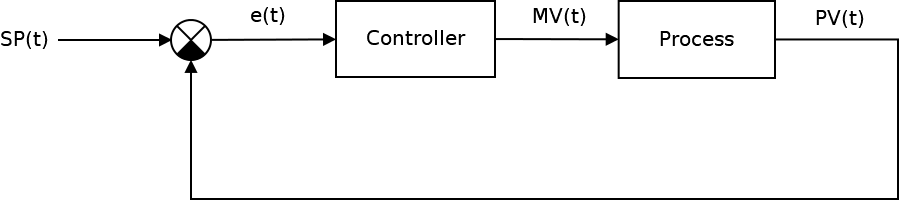
A key element of any ACS is the controller, which is a device that monitors the state of the control object and provides the required control law. The control process includes: calculating the control error or the error signal e ( t ) as the difference between the desired set point or SP and the current process vale or PV , after which the regulator generates the manipulated value or MV .

One type of regulator is the proportional-integral-differentiating (PID) controller , which generates a control signal, which is the sum of three components: proportional, integral and differential.

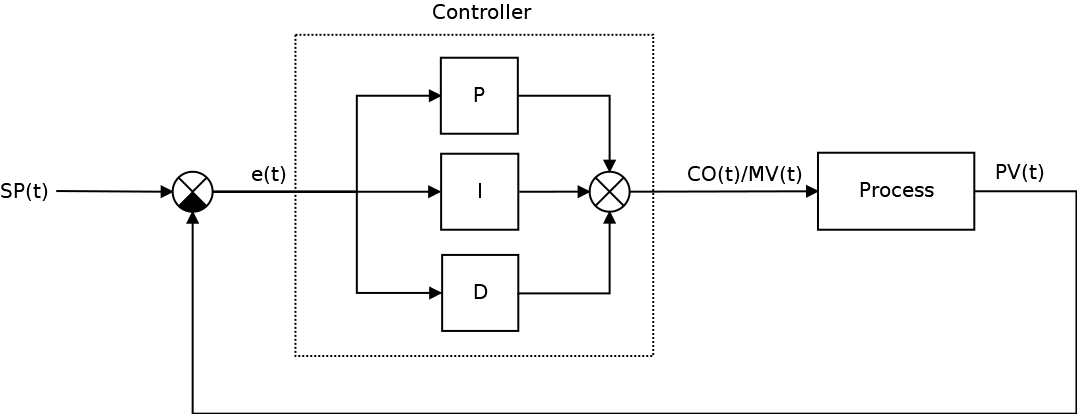
Where, $e (t)$ mismatch error as well, $P = K_p \ cdot e (t)$ - proportional, $I = K_i \ cdot \ int_0 ^ t e (\ tau) d \ tau$ - integral, $D = K_d \ cdot \ frac {de (t)} {dt}$ - the differential components (terms) of the control law, which in its final form is described by the following formulas

e (t) = S P (t) - P V (t),

$e (t) = SP (t) - PV (t),$

M V (t) = u n d e r b r a c e {K_{p} c d o t e (t)}_{P} + u n d e r b r a c e {K_{i} c d o t i n t_{0}^{t} e (t a u) d t a u}_{I} + u n d e r b r a c e {K_{d} c d o t f r a c d e (t) d t}_{D},

$MV (t) = \ underbrace {K_p \ cdot e (t)} _ {P} + \ underbrace {K_i \ cdot \ int_0 ^ te (\ tau) d \ tau} _ {I} + \ underbrace {K_d \ cdot \ frac {de (t)} {dt}} _ {D},$

Proportional component P - responsible for so-called. proportional control, the meaning of which is that the output signal of the regulator, counteracts the deviation of the controlled variable (the error of the error or else it is called the residual) from the specified value. The greater the error of the mismatch, the greater the command deviation of the regulator. This is the simplest and most obvious control law. The disadvantage of the proportional control law is that the regulator never stabilizes at a given value, and an increase in the proportionality coefficient always leads to self-oscillations. That is why in the appendage to the proportional control law one has to use integral and differential.

The integral component I accumulates (integrates) the regulation error, which allows the PID controller to eliminate the static error (steady-state error, residual mismatch). Or in other words: the integral link always introduces some displacement and if the system is subject to some constant errors, then it compensates them (at the expense of its displacement). But if these errors are not present or they are negligibly small, then the effect will be the opposite - the integral component itself will introduce an offset error. It is for this reason that it is not used, for example, in problems of ultra-precise positioning. A key disadvantage of the integral control law is the effect of saturating the integrator (Integrator windup).

The differential component D is proportional to the rate of change of the deviation of the controlled variable and is intended to counteract deviations from the target value, which are predicted in the future . It is noteworthy that the differential component eliminates damped oscillations. Differential regulation is especially effective for processes that have large delays. The disadvantage of the differential control law is its instability to the effect of noise (Differentiation noise).

Thus, depending on the situation, P-, PD-, PI- and PID-regulators can be applied, but the basic control law is mainly proportional (although in some specific tasks only the parts of differentiators and integrators can be used).

It would seem that the issue of the implementation of PID regulators has long been beaten and here on Habré there are a couple of quite good articles on this topic including Unity3D , there is also a good article PID Without a PhD ( translation ) and a series of articles in the journal "Modern Automation Technologies" in two parts: the first and second . Also at your service is an article on Wikipedia (the most complete read in English). And on the Unity3D community forums, no, no, and the PID controller pops up, just like on gamedev.stackexchange

When asked about the implementation of PID controllers is somewhat deeper than it seems. So much so that the young self-made, who have decided to implement such a regulatory scheme, will have many wonderful discoveries, and the topic is topical. So I hope this opus, someone come in handy, so let's get started.

Attempt number one

As an example, let us try to implement a regulation scheme using the example of controlling a turn in a simple 2D space arcade, step by step, starting from the very beginning (didn't you forget that this is a tutorial?).

Why not 3D? Because the implementation does not change, except that you have to turn up the PID controller to control pitch, yaw and roll. Although the question of the correct application of PID regulation together with quaternions is really interesting, it is possible that I will sanctify it in the future, but even in NASA Euler angles are preferred instead of quaternions, so we can do with a simple model on a two-dimensional plane.

To begin with, we will create the object itself of the game object of the spacecraft, which will consist of the ship object itself at the top level of the hierarchy, and attach the Engine object to it (purely for special effects). Here is how it looks from me:

And on the very object of the spacecraft we throw in the inspector of every component. Looking ahead, I will give a screen of how it will look at the end:

But this is later, but for now there are no scripts in it, only the standard gentleman's set: Sprite Render, RigidBody2D, Polygon Collider, Audio Source (why?).

Actually, physics now is the most important thing for us and control will be carried out exclusively through it, otherwise, the use of the PID controller would lose its meaning. The mass of our spacecraft will also be left at 1 kg, and all friction and gravity coefficients are zero - in space.

Since in addition to the spacecraft itself, there are a lot of other, less intelligent space objects, then we first describe the BaseBody parent class, which will contain references to our components, initialization and destruction methods, as well as a number of additional fields and methods, for example, to implement celestial mechanics:

BaseBody.cs

using UnityEngine; using System.Collections; using System.Collections.Generic; namespace Assets.Scripts.SpaceShooter.Bodies { [RequireComponent(typeof(SpriteRenderer))] [RequireComponent(typeof(AudioSource))] [RequireComponent(typeof(Rigidbody2D))] [RequireComponent(typeof(Collider2D))] public class BaseBody : MonoBehaviour { readonly float _deafultTimeDelay = 0.05f; [HideInInspector] public static List<BaseBody> _bodies = new List<BaseBody>(); #region RigidBody [HideInInspector] public Rigidbody2D _rb2d; [HideInInspector] public Collider2D[] _c2d; #endregion #region References [HideInInspector] public Transform _myTransform; [HideInInspector] public GameObject _myObject; /// <summary> /// ,     /// </summary> public GameObject _explodePrefab; #endregion #region Audio public AudioSource _audioSource; /// <summary> /// ,      /// </summary> public AudioClip[] _hitSounds; /// <summary> /// ,      /// </summary> public AudioClip[] _awakeSounds; /// <summary> /// ,     /// </summary> public AudioClip[] _deadSounds; #endregion #region External Force Variables /// <summary> ///      /// </summary> [HideInInspector] public Vector2 _ExternalForces = new Vector2(); /// <summary> ///    /// </summary> [HideInInspector] public Vector2 _V = new Vector2(); /// <summary> ///     /// </summary> [HideInInspector] public Vector2 _G = new Vector2(); #endregion public virtual void Awake() { Init(); } public virtual void Start() { } public virtual void Init() { _myTransform = this.transform; _myObject = gameObject; _rb2d = GetComponent<Rigidbody2D>(); _c2d = GetComponentsInChildren<Collider2D>(); _audioSource = GetComponent<AudioSource>(); PlayRandomSound(_awakeSounds); BaseBody bb = GetComponent<BaseBody>(); _bodies.Add(bb); } /// <summary> ///   /// </summary> public virtual void Destroy() { _bodies.Remove(this); for (int i = 0; i < _c2d.Length; i++) { _c2d[i].enabled = false; } float _t = PlayRandomSound(_deadSounds); StartCoroutine(WaitAndDestroy(_t)); } /// <summary> ///      /// </summary> /// <param name="waitTime"> </param> /// <returns></returns> public IEnumerator WaitAndDestroy(float waitTime) { yield return new WaitForSeconds(waitTime); if (_explodePrefab) { Instantiate(_explodePrefab, transform.position, Quaternion.identity); } Destroy(gameObject, _deafultTimeDelay); } /// <summary> ///    /// </summary> /// <param name="audioClip"> </param> /// <returns>  </returns> public float PlayRandomSound(AudioClip[] audioClip) { float _t = 0; if (audioClip.Length > 0) { int _i = UnityEngine.Random.Range(0, audioClip.Length - 1); AudioClip _audioClip = audioClip[_i]; _t = _audioClip.length; _audioSource.PlayOneShot(_audioClip); } return _t; } /// <summary> ///   /// </summary> /// <param name="damage"> </param> public virtual void Damage(float damage) { PlayRandomSound(_hitSounds); } } }

It seems they described everything that is necessary, even more than necessary (in the framework of this article). Now we will inherit from it the ship class Ship , which should be able to move and turn:

SpaceShip.cs

 using UnityEngine; using System.Collections; using System.Collections.Generic; namespace Assets.Scripts.SpaceShooter.Bodies { public class Ship : BaseBody { public Vector2 _movement = new Vector2(); public Vector2 _target = new Vector2(); public float _rotation = 0f; public void FixedUpdate() { float torque = ControlRotate(_rotation); Vector2 force = ControlForce(_movement); _rb2d.AddTorque(torque); _rb2d.AddRelativeForce(force); } public float ControlRotate(Vector2 rotate) { float result = 0f; return result; } public Vector2 ControlForce(Vector2 movement) { Vector2 result = new Vector2(); return result; } } }

While there is nothing interesting in it, at the current moment it is just a stub class.

We also describe the base (abstract) class for all BaseInputController input controllers:

BaseInputController.cs

 using UnityEngine; using Assets.Scripts.SpaceShooter.Bodies; namespace Assets.Scripts.SpaceShooter.InputController { public enum eSpriteRotation { Rigth = 0, Up = -90, Left = -180, Down = -270 } public abstract class BaseInputController : MonoBehaviour { public GameObject _agentObject; public Ship _agentBody; //      public eSpriteRotation _spriteOrientation = eSpriteRotation.Up; //    //   ""  "" public abstract void ControlRotate(float dt); public abstract void ControlForce(float dt); public virtual void Start() { _agentObject = gameObject; _agentBody = gameObject.GetComponent<Ship>(); } public virtual void FixedUpdate() { float dt = Time.fixedDeltaTime; ControlRotate(dt); ControlForce(dt); } public virtual void Update() { //TO DO } } }

Finally, PlayerFigtherInput Player Controller Class :

PlayerInput.cs

 using UnityEngine; using Assets.Scripts.SpaceShooter.Bodies; namespace Assets.Scripts.SpaceShooter.InputController { public class PlayerFigtherInput : BaseInputController { public override void ControlRotate(float dt) { //      Vector3 worldPos = Input.mousePosition; worldPos = Camera.main.ScreenToWorldPoint(worldPos); //     float dx = -this.transform.position.x + worldPos.x; float dy = -this.transform.position.y + worldPos.y; //  Vector2 target = new Vector2(dx, dy); _agentBody._target = target; //       float targetAngle = Mathf.Atan2(dy, dx) * Mathf.Rad2Deg; _agentBody._targetAngle = targetAngle + (float)_spriteOrientation; } public override void ControlForce(float dt) { // movement _agentBody._movement = Input.GetAxis("Vertical") * Vector2.up + Input.GetAxis("Horizontal") * Vector2.right; } } }

It seems to be finished, now you can finally move on to what it all was for, i.e. PID controllers (hope not forgotten?). Its implementation seems simple to ugliness:

 using System; using System.Collections.Generic; using System.Linq; using System.Text; namespace Assets.Scripts.Regulator { [System.Serializable] //          //      public class SimplePID { public float Kp, Ki, Kd; private float lastError; private float P, I, D; public SimplePID() { Kp = 1f; Ki = 0; Kd = 0.2f; } public SimplePID(float pFactor, float iFactor, float dFactor) { this.Kp = pFactor; this.Ki = iFactor; this.Kd = dFactor; } public float Update(float error, float dt) { P = error; I += error * dt; D = (error - lastError) / dt; lastError = error; float CO = P * Kp + I * Ki + D * Kd; return CO; } } }

We take the default values of the coefficients from the ceiling: this will be a trivial unit coefficient of the proportional control law Kp = 1, a small coefficient value for the differential control law Kd = 0.2, which should eliminate the expected fluctuations and a zero value for Ki, which is chosen because there are no static errors in the model (but you can always make them, and then heroically fight with the help of an integrator).

Now let's return to our SpaceShip class and try to use our creation as a spacecraft rotation control in the ControlRotate method:

  public float ControlRotate(Vector2 rotate) { float MV = 0f; float dt = Time.fixedDeltaTime; //  float angleError = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle); //   MV = _angleController.Update(angleError, dt); return MV; }

The PID controller will perform the exact angular positioning of the spacecraft only at the expense of torque . Everything is fair, physics and ACS, almost like in real life.

And without these your Quaternion.Lerp

  if (!_rb2d.freezeRotation) rb2d.freezeRotation = true; float deltaAngle = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle); float T = dt * Mathf.Abs( _rotationSpeed / deltaAngle); //     Quaternion rot = Quaternion.Lerp( _myTransform.rotation, Quaternion.Euler(new Vector3(0, 0, targetAngle)), T); //    _myTransform.rotation = rot;

The resulting Ship.cs source code under the spoiler

 using UnityEngine; using Assets.Scripts.Regulator; namespace Assets.Scripts.SpaceShooter.Bodies { public class Ship : BaseBody { public GameObject _flame; public Vector2 _movement = new Vector2(); public Vector2 _target = new Vector2(); public float _targetAngle = 0f; public float _angle = 0f; [Header("PID")] public SimplePID _angleController = new SimplePID(); public void FixedUpdate() { float torque = ControlRotate(_targetAngle); Vector2 force = ControlForce(_movement); _rb2d.AddTorque(torque); _rb2d.AddRelativeForce(force); } public float ControlRotate(float rotate) { float MV = 0f; float dt = Time.fixedDeltaTime; _angle = _myTransform.eulerAngles.z; //  float angleError = Mathf.DeltaAngle(_angle, rotate); //   MV = _angleController.Update(angleError, dt); return MV; } public Vector2 ControlForce(Vector2 movement) { Vector2 MV = new Vector2(); //      if (movement != Vector2.zero) { if (_flame != null) { _flame.SetActive(true); } } else { if (_flame != null) { _flame.SetActive(false); } } MV = movement; return MV; } } }

Everything? Going home?

WTF! What's happening? Why does the ship turn strange? And why does he rebound so sharply from other objects? Is this stupid PID controller not working?

Do not panic! Let's try to figure out what's going on.

At the moment of receiving a new SP value, an abrupt (stepwise) jump in the error mismatch occurs, which, as we remember, is calculated like this: $e (t) = SP (t) - PV (t),$ accordingly, there is a sharp jump in the error $\ frac {de (t)} {dt}$ , which we calculate in this line of code:

 D = (error - lastError) / dt;

You can, of course, try other differentiation schemes , for example, three-point, or five-point, or ... but still it will not help. Well, derivatives of sharp jumps do not like - at such points the function is not differentiable . However, experimenting with different schemes of differentiation and integration is worth it, but then not in this article.

I think that the moment has come to build the transition graphs: a step effect from S (t) = 0 in SP (t) = 90 degrees for a body weighing 1 kg, a long arm of a force of 1 meter and a step of differentiation grid of 0.02 s - just like in ours for the Unity3D example (in fact, not quite, when building these graphs it was not taken into account that the moment of inertia depends on the geometry of the solid body, therefore the transition process will be slightly different, but still quite similar for demonstration). All values on the bar are given in absolute values: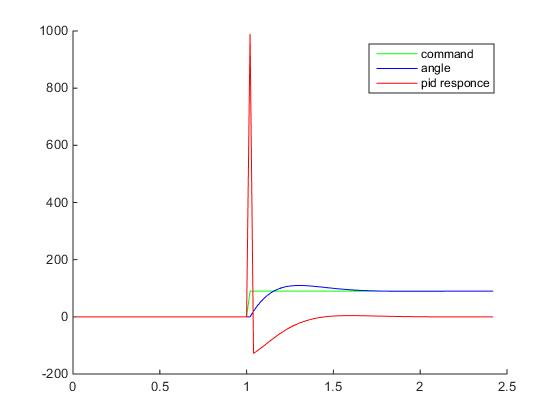

Hm, what's going on here? Where did the PID response go?

Congratulations, we have just come across such a thing as a kick. Obviously, at the point in time when the process is still PV = 0, and the setpoint is already SP = 90, then by numerical differentiation we will get a derivative value of about 4500, which will be multiplied by Kd = 0.2 and will be added to the proportional term, so that the output will be angular acceleration is 990, and this is a formal abuse of the physical model of Unity3D (angular speeds will reach 18,000 degrees / s ... I think this is the limiting value of the angular velocity for RigidBody2D).

Maybe you should pick up the coefficients with handles, so that the jump was not so strong?
Not! The best thing we can achieve in this way is a small amplitude of the jump in the derivative, but the jump itself will remain as it was, and you can get to the total inefficiency of the differential component.

But you can experiment.

Attempt number two. Saturation

It is logical that the drive (in our case, the virtual shunting engines SpaceShip), can not work as many large values as our crazy regulator can produce. So the first thing we do is saturate the regulator output:

 public float ControlRotate(Vector2 rotate, float thrust) { float CO = 0f; float MV = 0f; float dt = Time.fixedDeltaTime; //  float angleError = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle); //   CO = _angleController.Update(angleError, dt); // MV = CO; if (MV > thrust) MV = thrust; if (MV< -thrust) MV = -thrust; return MV; }

And once again, the rewritten Ship class looks like this.

 namespace Assets.Scripts.SpaceShooter.Bodies { public class Ship : BaseBody { public GameObject _flame; public Vector2 _movement = new Vector2(); public Vector2 _target = new Vector2(); public float _targetAngle = 0f; public float _angle = 0f; public float _thrust = 1f; [Header("PID")] public SimplePID _angleController = new SimplePID(0.1f,0f,0.05f); public void FixedUpdate() { _torque = ControlRotate(_targetAngle, _thrust); _force = ControlForce(_movement); _rb2d.AddTorque(_torque); _rb2d.AddRelativeForce(_force); } public float ControlRotate(float targetAngle, float thrust) { float CO = 0f; float MV = 0f; float dt = Time.fixedDeltaTime; //  float angleError = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle); //   CO = _angleController.Update(angleError, dt); // MV = CO; if (MV > thrust) MV = thrust; if (MV< -thrust) MV = -thrust; return MV; } public Vector2 ControlForce(Vector2 movement) { Vector2 MV = new Vector2(); if (movement != Vector2.zero) { if (_flame != null) { _flame.SetActive(true); } } else { if (_flame != null) { _flame.SetActive(false); } } MV = movement * _thrust; return MV; } public void Update() { } } }

The final scheme of our ACS then it will become such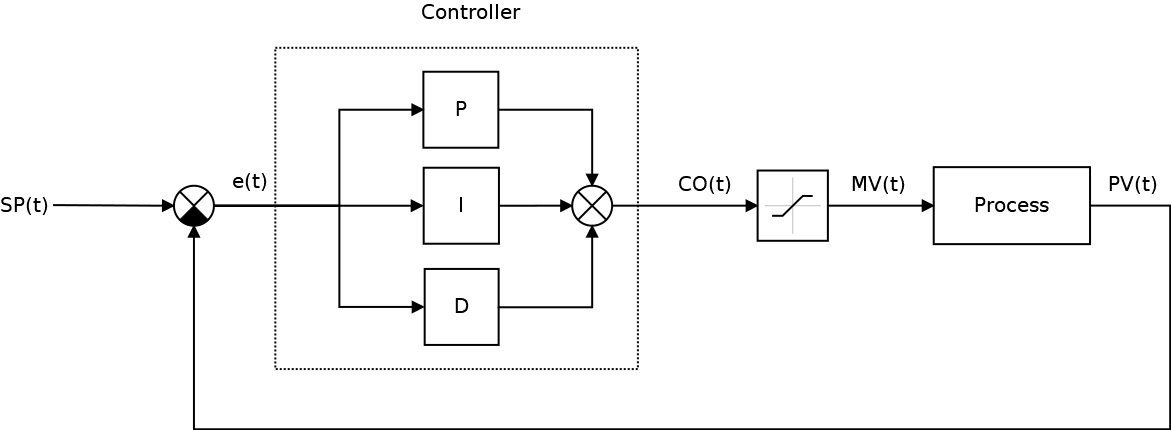

In this case, it becomes clear that the output of the CO (t) controller is not the same a bit, that the controlled value of the MV (t) process.

Actually from this place you can already add a new game entity - a drive through which the process control will be exercised, the operation logic of which may be more complicated than just Mathf.Clamp (), for example, you can enter a discretization of values (so as not to overload the game physics with values the sixths after the comma), the dead zone (again, it does not make sense to overload physics with super-small reactions), introduce a delay into the control and nonlinearity (for example, sigmoid) of the drive, and then see what happens.

By launching the game, we find that the spacecraft has finally become controllable:

If you build graphics, you can see that the controller’s response has already become this: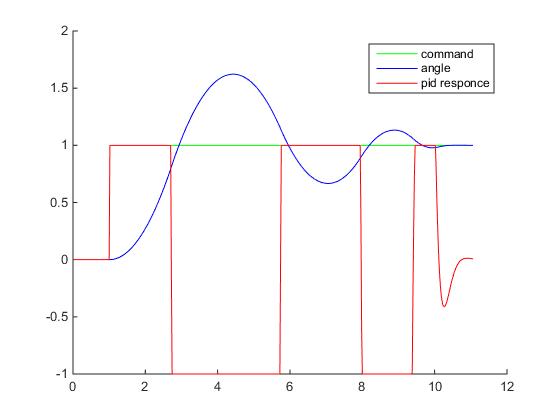

Here, the normalized values are already used, the angles are divided by the SP value, and the controller output is normalized relative to the maximum value at which the saturation already occurs.

Now the graph shows the presence of overshooting error and damped oscillations. By reducing Kp and increasing Kd, it is possible to reduce oscillations, but it will increase the controller's response time (the ship’s turn speed). Conversely, by increasing Kp and decreasing Kd - it is possible to increase the speed of the controller’s reaction, but parasitic oscillations will appear that, at certain (critical) values, will cease to be damped.

Below is a known table of the effect of increasing the parameters of the PID controller ( how to reduce the font, and then the hyphenation table does not climb? ):

Term	Rise time	Overshoot error	Transition time	Steady error	Stability
Kp	Reduction	Increase	Slight changes	Decreases	Degrades
Ki	Decreases	Increases	Increases	Compensated if there is	Degrades
Kd	Slight changes	Decreases	Decreases		Increases if Kd is small

And the general algorithm for manually tuning the PID controller is as follows:

We select proportional coefficients at disconnected differential and integral links until self-oscillations begin.
Gradually increasing the differential component get rid of auto-oscillations
If there is a residual regulation error (offset), then we eliminate it due to the integral component.

There are no general values of the PID controller parameters: specific values depend solely on the process parameters (its transfer characteristic ): the PID controller perfectly working with one control object will not work with the other. Moreover, the coefficients of the proportional, integral and differential components are also interdependent.

In general, let's not talk about sad things, the most interesting things are waiting for us ...

Attempt number three. Once again derivatives

Having attached a crutch in the form of restriction of the controller's output values, we have not solved the most important problem of our regulator - the differential component feels bad when the error at the regulator input changes stepwise. In fact, there are many other crutches, for example, at the time of a spasmodic change of the SP, “disconnect” the differential component or put low-pass filters between the SP (t) and the operation $SP (t) -PV (t)$ due to which there will be a smooth increase of the error, and you can completely turn around and see the real Kalman filter for smoothing the input data. In general, there are many crutches, and of course I would like to add an observer , but not this time.

Therefore, let us return to the derivative of the error of the mismatch again and take a close look at it:

f r a c d e (t) d t = f r a c d (S P (t) - P V (t)) d t = f r a c d S P (t) d t - f r a c d P V (t) d t,

$\ frac {de (t)} {dt} = \ frac {d (SP (t) -PV (t))} {dt} = \ frac {dSP (t)} {dt} - \ frac {dPV ( t)} {dt},$

Did you notice anything? If you look closely, you may find that, in general, SP (t) does not change in time (except for the moments of step change when the controller receives a new command), i.e. its derivative is zero:

f r a c d S P (t) d t = 0,

$\ frac {dSP (t)} {dt} = 0,$

then

f r a c d e (t) d t = - f r a c d P V (t) d t,

$\ frac {de (t)} {dt} = - \ frac {dPV (t)} {dt},$

In other words, instead of the derivative error, which is not differentiable everywhere, we can use the derivative of the process, which in the world of classical mechanics is usually continuous and differentiated everywhere, and the scheme of our ACS already takes the following form: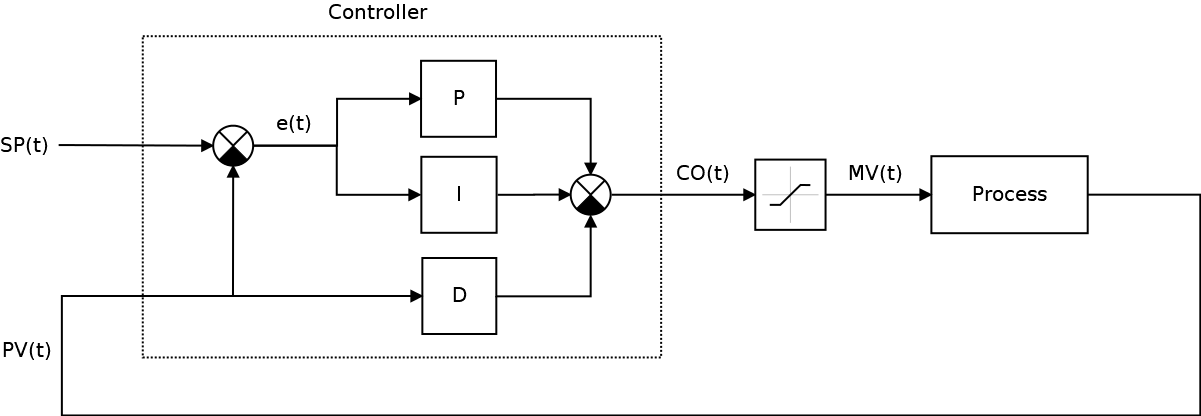

e (t) = S P (t) - P V (t),

$e (t) = SP (t) - PV (t),$

C O (t) = u n d e r b r a c e {K_{p} c d o t e (t)}_{P} + u n d e r b r a c e {K_{i} c d o t i n t_{0}^{t} e (t a u) d t a u}_{I} - u n d e r b r a c e {K_{d} c d o t f r a c d P V (t) d t}_{D},

$CO (t) = \ underbrace {K_p \ cdot e (t)} _ {P} + \ underbrace {K_i \ cdot \ int_0 ^ te (\ tau) d \ tau} _ {I} - \ underbrace {K_d \ cdot \ frac {dPV (t)} {dt}} _ {D},$

Modify the controller code:

 using System; using System.Collections.Generic; using System.Linq; using System.Text; namespace Assets.Scripts.Regulator { [System.Serializable] public class SimplePID { public float Kp, Ki, Kd; private float P, I, D; private float lastPV = 0f; public SimplePID() { Kp = 1f; Ki = 0f; Kd = 0.2f; } public SimplePID(float pFactor, float iFactor, float dFactor) { this.Kp = pFactor; this.Ki = iFactor; this.Kd = dFactor; } public float Update(float error, float PV, float dt) { P = error; I += error * dt; D = -(PV - lastPV) / dt; lastPV = PV; float CO = Kp * P + Ki * I + Kd * D; return CO; } } }

And change the ControlRotate method a bit:

 public float ControlRotate(Vector2 rotate, float thrust) { float CO = 0f; float MV = 0f; float dt = Time.fixedDeltaTime; //  float angleError = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle); //   CO = _angleController.Update(angleError, _myTransform.eulerAngles.z, dt); // MV = CO; if (CO > thrust) MV = thrust; if (CO < -thrust) MV = -thrust; return MV; }

And-and-and-and ... if you start the game, you will see that in fact nothing has changed since the last attempt, which is what was required to prove. However, if you remove the saturation, the graph of the reaction of the regulator will look like this: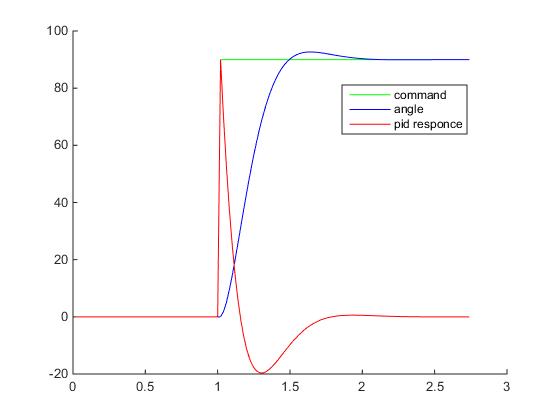

The CO (t) jump is still present, but it is not as big as it was at the very beginning, and most importantly, it has become predictable, since is provided exclusively by the proportional component, and is limited by the maximum possible error of the mismatch and proportional to the coefficient of the PID controller (and this already hints that it makes sense to choose Kp is still less than one, for example, 1 / 90f), but does not depend on the differentiation grid step ( i.e. dt ). In general, I strongly recommend using exactly the derivative of the process, not errors.

I think now no one will be surprised, but in the same Makar can be replaced $K_p \ cdot e (t)$ on $-K_p \ cdot PV (t)$ however, we will not dwell on this, you can experiment and tell in the comments what came out of it (most interestingly)

Attempt number four. Alternative implementations of the PID controller

In addition to the ideal representation of the PID controller described above, the standard form is often used in practice, without the Ki and Kd coefficients, instead of which time constants are used.

This approach is due to the fact that a number of PID controller tuning techniques are based on the frequency characteristics of the PID controller and process. Actually, all the TAU and revolves around the frequency characteristics of the processes, so for those who want to go deeper, and, suddenly, faced with an alternative nomenclature, I will give an example of the so-called. standard form of PID controller:

e (t) = S P (t) - P V (t),

$e (t) = SP (t) - PV (t),$

C O (t) = C O_{b i a s} + K_{p} c d o t B i g l (e (t) + f r a c 1 T_{i} c d o t i n t_{0}^{t} e (t a u) d t a u - T_{d} c d o t f r a c d P V (t) d t B i g l),

$CO (t) = CO_ {bias} + K_p \ cdot \ Bigl (e (t) + \ frac {1} {T_i} \ cdot \ int_0 ^ te (\ tau) d \ tau - T_d \ cdot \ frac { dPV (t)} {dt} \ Bigl),$

Where, $T_d = \ frac {K_d} {K_p}$ - constant differentiation, affecting the prediction of the system state by the regulator
$T_i = \ frac {K_p} {K_i}$ - the integration constant affecting the error averaging interval by the integral link.

The basic principles of tuning a PID controller in standard form are similar to the idealized PID controller:

an increase in the proportional coefficient increases the speed and reduces the stability margin
with a decrease in the integral component of the regulation error over time decreases faster;
a decrease in the continuous integration reduces the stability margin;
the increase in the differential component increases the stability margin and speed

The source code of the standard form, you can find under the spoiler

 namespace Assets.Scripts.Regulator { [System.Serializable] public class StandartPID { public float Kp, Ti, Td; public float error, CO; public float P, I, D; private float lastPV = 0f; public StandartPID() { Kp = 0.1f; Ti = 10000f; Td = 0.5f; bias = 0f; } public StandartPID(float Kp, float Ti, float Td) { this.Kp = Kp; this.Ti = Ti; this.Td = Td; } public float Update(float error, float PV, float dt) { this.error = error; P = error; I += (1 / Ti) * error * dt; D = -Td * (PV - lastPV) / dt; CO = Kp * (P + I + D); lastPV = PV; return CO; } } }

As default values, Kp = 0.01, Ti = 10000, Td = 0.5 are chosen - with such values the ship turns quickly enough and has some stability margin.

In addition to this form of the PID controller, so-called recurrent form :

C O (t_{k}) = C O (t_{k - 1}) + K_{p} l e f t [l e f t (1 + d f r a c D e l t a t T_{i} + d f r a c T_{d} D e l t a t r i g h t) e (t_{k}) + l e f t (- 1 - d f r a c 2 T_{d} D e l t a t r i g h t) e (t_{k - 1}) + d f r a c T_{d} D e l t a t e (t_{k - 2}) r i g h t]

$CO (t_k) = CO (t_ {k-1}) + K_p \ left [\ left (1+ \ dfrac {\ Delta t} {T_i} + \ dfrac {T_d} {\ Delta t} \ right) e (t_k) + \ left (-1- \ dfrac {2T_d} {\ Delta t} \ right) e (t_ {k-1}) + \ dfrac {T_d} {\ Delta t} e (t_ {k-2 }) \ right]$

We will not dwell on it, because It is relevant primarily for hardware programmers working with FPGAs and microcontrollers, where such an implementation is much more convenient and efficient. In our case - let's do something on Unity3D piles - this is just another implementation of the PID controller, which is no better than others and even less understandable, so once again we will rejoice together how well to program in cozy C #, and not terribly and scary vhdl for example.

Instead of a conclusion. Where else to add the PID controller

Now we will try to complicate the ship control a little using dual-loop control: one PID controller, already familiar to us _angleController, is still responsible for the angular positioning, but the second - new, _angularVelocityController - controls the speed of rotation:

 public float ControlRotate(float targetAngle, float thrust) { float CO = 0f; float MV = 0f; float dt = Time.fixedDeltaTime; _angle = _myTransform.eulerAngles.z; //   float angleError = Mathf.DeltaAngle(_angle, targetAngle); float torqueCorrectionForAngle = _angleController.Update(angleError, _angle, dt); //   float angularVelocityError = -_rb2d.angularVelocity; float torqueCorrectionForAngularVelocity = _angularVelocityController.Update(angularVelocityError, -angularVelocityError, dt); //   CO = torqueCorrectionForAngle + torqueCorrectionForAngularVelocity; //   100 CO = Mathf.Round(100f * CO) / 100f; // MV = CO; if (CO > thrust) MV = thrust; if (CO < -thrust) MV = -thrust; return MV; }

— , — , . [] , — , , .

, — PlayerInputCorvette, "-", - , , . _turnRate — / ( InputCOntroller Ship).

 public class PlayerCorvetteInput : BaseInputController { public float _turnSpeed = 90f; public override void ControlRotate() { //    Vector3 worldPos = Input.mousePosition; worldPos = Camera.main.ScreenToWorldPoint(worldPos); //      float dx = -this.transform.position.x + worldPos.x; float dy = -this.transform.position.y + worldPos.y; //    Vector2 target = new Vector2(dx, dy); _agentBody._target = target; //       _agentBody._rotation -= Input.GetAxis("Horizontal") * _turnSpeed * Time.deltaTime; } public override void ControlForce() { // movement _agentBody._movement = Input.GetAxis("Vertical") * Vector2.up; } }

 namespace Assets.Scripts.SpaceShooter.UI { [RequireComponent(typeof(Ship))] [RequireComponent(typeof(BaseInputController))] public class Debugger : MonoBehaviour { Ship _ship; BaseInputController _controller; List<SimplePID> _pids = new List<SimplePID>(); List<string> _names = new List<string>(); Vector2 _orientation = new Vector2(); // Use this for initialization void Start() { _ship = GetComponent<Ship>(); _controller = GetComponent<BaseInputController>(); _pids.Add(_ship._angleController); _names.Add("Angle controller"); _pids.Add(_ship._angularVelocityController); _names.Add("Angular velocity controller"); } // Update is called once per frame void Update() { DrawDebug(); } Vector3 GetDiretion(eSpriteRotation spriteRotation) { switch (_controller._spriteOrientation) { case eSpriteRotation.Rigth: return transform.right; case eSpriteRotation.Up: return transform.up; case eSpriteRotation.Left: return -transform.right; case eSpriteRotation.Down: return -transform.up; } return Vector3.zero; } void DrawDebug() { //  Vector3 vectorToTarget = transform.position + 5f * new Vector3(-Mathf.Sin(_ship._targetAngle * Mathf.Deg2Rad), Mathf.Cos(_ship._targetAngle * Mathf.Deg2Rad), 0f); //   Vector3 heading = transform.position + 4f * GetDiretion(_controller._spriteOrientation); //  Vector3 torque = heading - transform.right * _ship._Torque; Debug.DrawLine(transform.position, vectorToTarget, Color.white); Debug.DrawLine(transform.position, heading, Color.green); Debug.DrawLine(heading, torque, Color.red); } void OnGUI() { float x0 = 10; float y0 = 100; float dx = 200; float dy = 40; float SliderKpMax = 1; float SliderKpMin = 0; float SliderKiMax = .5f; float SliderKiMin = -.5f; float SliderKdMax = .5f; float SliderKdMin = 0; int i = 0; foreach (SimplePID pid in _pids) { y0 += 2 * dy; GUI.Box(new Rect(25 + x0, 5 + y0, dx, dy), ""); pid.Kp = GUI.HorizontalSlider(new Rect(25 + x0, 5 + y0, 200, 10), pid.Kp, SliderKpMin, SliderKpMax); pid.Ki = GUI.HorizontalSlider(new Rect(25 + x0, 20 + y0, 200, 10), pid.Ki, SliderKiMin, SliderKiMax); pid.Kd = GUI.HorizontalSlider(new Rect(25 + x0, 35 + y0, 200, 10), pid.Kd, SliderKdMin, SliderKdMax); GUIStyle style1 = new GUIStyle(); style1.alignment = TextAnchor.MiddleRight; style1.fontStyle = FontStyle.Bold; style1.normal.textColor = Color.yellow; style1.fontSize = 9; GUI.Label(new Rect(0 + x0, 5 + y0, 20, 10), "Kp", style1); GUI.Label(new Rect(0 + x0, 20 + y0, 20, 10), "Ki", style1); GUI.Label(new Rect(0 + x0, 35 + y0, 20, 10), "Kd", style1); GUIStyle style2 = new GUIStyle(); style2.alignment = TextAnchor.MiddleLeft; style2.fontStyle = FontStyle.Bold; style2.normal.textColor = Color.yellow; style2.fontSize = 9; GUI.TextField(new Rect(235 + x0, 5 + y0, 60, 10), pid.Kp.ToString(), style2); GUI.TextField(new Rect(235 + x0, 20 + y0, 60, 10), pid.Ki.ToString(), style2); GUI.TextField(new Rect(235 + x0, 35 + y0, 60, 10), pid.Kd.ToString(), style2); GUI.Label(new Rect(0 + x0, -8 + y0, 200, 10), _names[i++], style2); } } } }

Ship :

 namespace Assets.Scripts.SpaceShooter.Bodies { public class Ship : BaseBody { public GameObject _flame; public Vector2 _movement = new Vector2(); public Vector2 _target = new Vector2(); public float _targetAngle = 0f; public float _angle = 0f; public float _thrust = 1f; [Header("PID")] public SimplePID _angleController = new SimplePID(0.1f,0f,0.05f); public SimplePID _angularVelocityController = new SimplePID(0f,0f,0f); private float _torque = 0f; public float _Torque { get { return _torque; } } private Vector2 _force = new Vector2(); public Vector2 _Force { get { return _force; } } public void FixedUpdate() { _torque = ControlRotate(_targetAngle, _thrust); _force = ControlForce(_movement, _thrust); _rb2d.AddTorque(_torque); _rb2d.AddRelativeForce(_force); } public float ControlRotate(float targetAngle, float thrust) { float CO = 0f; float MV = 0f; float dt = Time.fixedDeltaTime; _angle = _myTransform.eulerAngles.z; //   float angleError = Mathf.DeltaAngle(_angle, targetAngle); float torqueCorrectionForAngle = _angleController.Update(angleError, _angle, dt); //   float angularVelocityError = -_rb2d.angularVelocity; float torqueCorrectionForAngularVelocity = _angularVelocityController.Update(angularVelocityError, -angularVelocityError, dt); //   CO = torqueCorrectionForAngle + torqueCorrectionForAngularVelocity; //   100 CO = Mathf.Round(100f * CO) / 100f; // MV = CO; if (CO > thrust) MV = thrust; if (CO < -thrust) MV = -thrust; return MV; } public Vector2 ControlForce(Vector2 movement, float thrust) { Vector2 MV = new Vector2(); if (movement != Vector2.zero) { if (_flame != null) { _flame.SetActive(true); } } else { if (_flame != null) { _flame.SetActive(false); } } MV = movement * thrust; return MV; } public void Update() { } } }