Coding with the withdrawal of information. Part 2, Mathematical

Introduction

In the previous part, the principal possibility of coding was considered, in which, in case you can isolate the common part of the key and the message, you can transmit less information than there is in the original message.

Let me tell you a little about where this topic came from. A long time ago, from one good person, I took ivlad to read and now I can’t give (please forgive) an interesting book [1], where it is written: “In turn, the cryptography itself can be divided into two areas, known as permutation and replacement” .

Accordingly, almost immediately the following questions appeared:

because permutation and replacement preserve the amount of information, is it possible to do so in order to circumvent this restriction, and transfer information less than it is in the message - from here (from “whether it’s not weak”) the first part was born;
if the problem seems to be solved, then whether there is a solution itself and at least a fraction of the mathematical meaning in it - this question is the theme of this part;
Is there any practical sense in all this? The question is still open.

What do the crow and the desk have in common?

The picture is taken from here .
The riddle of Carroll in the title is given as an illustration of the problem that needs to be solved. Namely: define a couple of functions $E (k, m)$ - coding and $D (k, s)$ - decoding satisfying the following conditions:

$I (E (k, m)) \ le I (m)$ –The amount of information transmitted by Shannon is less than the amount of information in the original message
$D (k, E (k, m)) = m$ - the decoding function applied to the encoded message will allow to unambiguously restore the original message.

Here $I (m)$ - the amount of information on Shannon [2] (assuming that all characters are equally likely, which is not true in general, but is used for simplicity of presentation) in the message $m$ , $k$ - key, $c = E (k, m)$ - coded message.

In order to simplify further reasoning, let us restrict ourselves to further messages that can be numerically constrained, which on the one hand does not particularly limit us (since you can assign an appropriate numeric code to any character), and on the other, allow you to use mathematics in the right amount.

So, consider first for example two numbers $k = 746,130$ and $m = 50 133 666$ and using the main theorem of arithmetic [4] (any natural can be decomposed into a product of simple) we find the following parameters:

Smallest common factor $k$ and $m$ - $GCD (k, m) = $ 1,25$ its simple dividers $[2,3,11,19]$ ,
Private $m / gcd (k, m) = $ 59$ and its simple dividers $[5,7,17]$ which we denote as $s_0$ ,
Decomposition number $m$ to prime factors: $[2,3,11,19, 39 979]$ ,
Decomposition number $k$ to prime factors: $[2,3,5,7,11,17,19]$ .

Let's write all this in tabular form, where the general part of the information between the key and the message is marked in blue, the information is unique for the key in yellow, and the message is unique in orange:

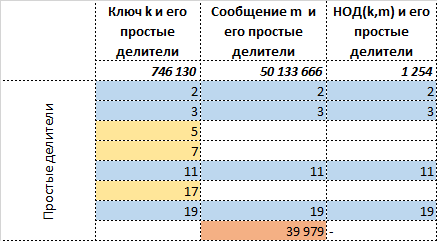
Immediately it becomes clear that

G c d (k, m)

$Gcd (k, m)$ is a common part between the key

k

$k$ and message

m

$m$ that both the sender and the recipient have. Thus, ideally, of course, and not in reality, it is enough to transmit information about:
')

unique to the message information - that does not apply to $k$ those. $[39 979]$ , namely $s_0 = 39 979$ ,

the very $Gcd (k, m)$ but so that it cannot be restored.

Mark now the positions of simple dividers $Gcd (k, m)$ common with simple dividers $k$ , units, and the rest, except maybe the leading position - zeros.

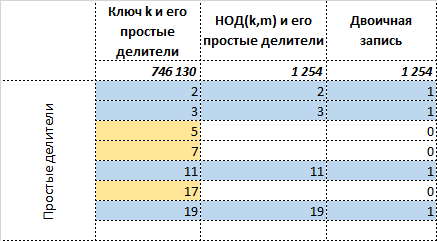
The resulting number

s_{1} = 1010011 = $ 8

$s_1 = 1010011 = $ 8$ sufficiently characterizes

G C D

$GCD$ , thereby allowing the original message to be restored. Those. getting two numbers to the input

[39979, 83]

$[39 979, 83]$ you need to do a fairly simple inverse transformation:

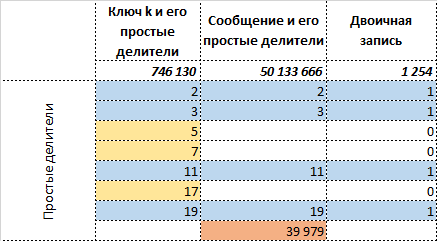
If we now estimate the length of the original message in binary form

l e n_{2} (m) = l e n_{2} ([1111010000011100100000100]) = $ 2

$len_2 (m) = len_2 ([1111010000011100100000100]) = $ 2$ and messages

l e n_{2} ([c_{0}, c_{1}]) = l e n_{2} ([1001110000101011, 1010011]) = $ 2

$len_2 ([c_0, c_1]) = len_2 ([1001110000101011, 1010011]) = $ 2$ you can see that you can save the message length in

3

$3$ bit, the same with the amount of information

I (m) = 13

$I (m) = 13$ bit,

I (c) = I ([c_{0}, c_{1}]) = 11.5

$I (c) = I ([c_0, c_1]) = 11.5$ bit Here is the function

l e n_{2} (c d o t)

$len_2 (\ cdot)$ - the length of the number in binary form.

Thus, to put it in words from the well-known anecdote, "in Scotland there is at least one sheep, black at least on one side" [3].

So, at the moment we have - this coding method is suitable, but only for pairs of numbers that have the same divisor in the decomposition. Otherwise, if, for example, we take simple numbers as a key and as a message, we obviously cannot reduce anything, but only increase the length of the message, as well as the amount of information transmitted, which is not what we wanted. The same situation is repeated in the case when, for example,

G C D (k, m) < 2

$GCD (k, m) <2$ or

l e n_{2} (c_{1}) \geq l e n_{2} (g c d (k, m))

$len_2 (c_1) ≥ len_2 (gcd (k, m))$ because savings will be either minimal or absent in principle.

What to do…

in order to increase the likelihood of success with this coding method?
In general, if you look closely at the key, it is clear that it is not bad divided into prime numbers $2,3,5,7,11,17,19$ what is done specifically for the success of the operation of finding $Gcd (k, m)$ . Since such an operation can negatively affect the number of keys used, then determining the order of simple factors and making it part of the key information, we obtain, although not radical, an increase in the number of encoding options that positively affect the number of keys. Using a number instead of a key $[746,130]$ and a couple $[746 130, 0125763]$ where the second number represents the order of multiplication and determines the value $c_1$ .

The next problem to be effectively solved is the ratio of the frequencies of the appearance of primes and powers of two, it is easy to notice that the coding efficiency of powers of two rather quickly decreases with increasing length $c_1$ (see the graph of the corresponding sequences if there is one common simple divisor) and depends mainly on the number of key dividers and their values.

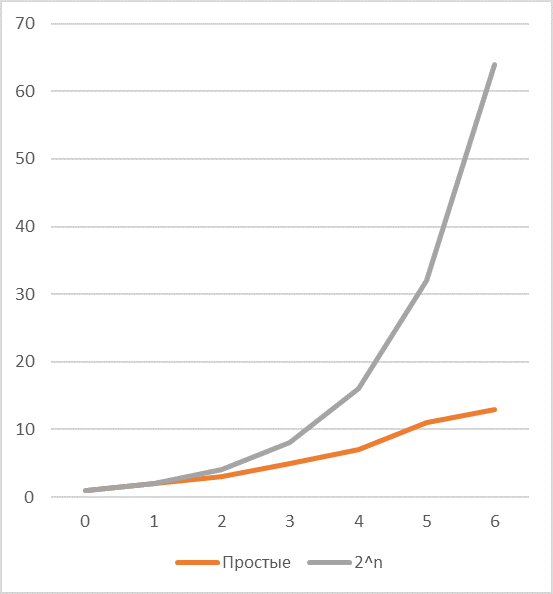
In case, there are two common dividers and one of them, for example, is

3

$3$ , then opportunities for savings increase very noticeably.

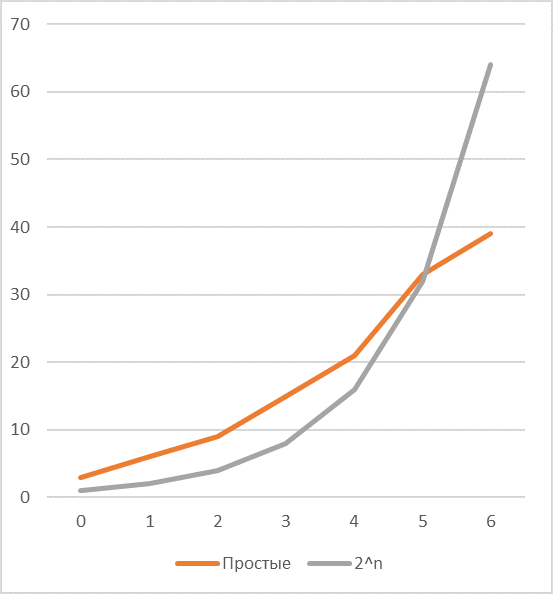
Which means that for efficient coding you need to come up with a more efficient coding method

c_{1}

$c_1$ .

That is, it makes sense to continue the subject further.

Example

As usual, they are laid out on github [5] - Excel is used because many have it and there is no need to think about compatibility. There are two bookmarks in the file:

"Test" - the calculations themselves, because they are quite actively using the Excel function "CASE ()" and the key and message numbers can be mutually simple, then you have to step into some cell and press enter to get the desired savings (results in lines 31-36);
“Example 1” - examples of ready calculations are given, since chance in excel does not leave them a chance to repeat.

Coding with the withdrawal of information. Part 2, Mathematical

Introduction

What do the crow and the desk have in common?

What to do…

Example

Links

More articles: