We try q-learning to taste, the story in three parts
This article is a short note on the implementation of the q-learning algorithm for managing an agent in a stochastic environment. The first part of the article will be devoted to creating an environment for carrying out simulations - mini-games on the nxn field, in which the agent must hold out for a long time at a distance from opponents moving randomly. The task of the opponents, respectively, to overtake him. Points are awarded for each move made by the agent in the simulation. The second part of the article will cover the basics of the q-learning algorithm and its implementation. In the third part, we will try to change the parameters that determine the perception of the environment by the agent. Let us analyze the influence of these parameters on the performance of his game. I specifically shifted the emphasis towards using a minimum number of third-party modules. The goal is to touch the essence of the algorithm, to touch it, so to speak. For implementation we will use only "pure" python 3.
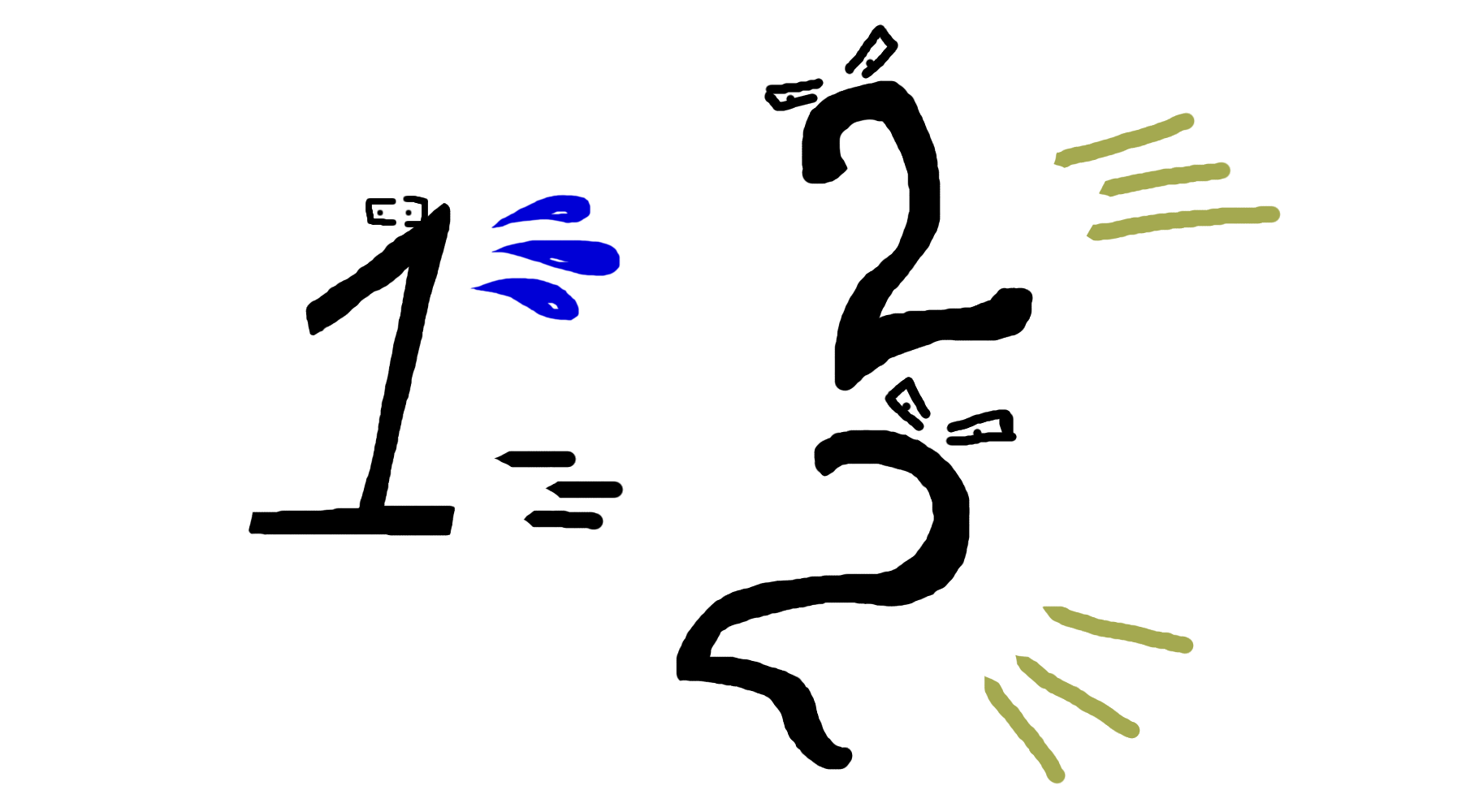
The medium in which the agent operates is represented by a two-dimensional field of size n. This is how it looks like:
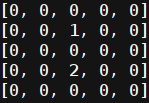
')
Here the unit is represented by the agent, the deuce is marked with the opponent Now we turn directly to the code. Variables that describe the environment: field size, agent, list of opponents.
Typical actor: agent or adversary.
Agent description.
The strategy of the agent, while empty.
Each of the participants in the simulation can make a move in any direction, including diagonally, the actor can also not move at all. The set of allowed movements on the example of the enemy:
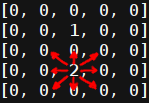
Thanks to the diagonal movements, the enemy always has the opportunity to overtake the agent, no matter how hard he tries to leave. This provides a finite number of simulation moves for any degree of agent training. Let's write its possible actions with the validation of the offset. The method takes the change in the coordinates of the agent and updates its position
Description of the enemy.
Moving an adversary with offset validation. The method does not exit the cycle until the condition of the course validity is satisfied.
One step simulation. Update the position of the enemy and the agent.
Visualization of the work of the simulation.
Simulation, the main stages:
1. Registration of coordinates of actors.
2. Check the achievement of conditions for the completion of the simulation.
3. Start the update cycle of the simulation.
- Drawing environment.
- Update simulation state.
- Registration of coordinates of actors.
- Check the achievement of conditions for the completion of the simulation.
4. Drawing the environment.
Initialization of the environment and launch.
The q-learning method is based on the introduction of the Q function, reflecting the value of each possible agent action a for the current state s, in which the simulation is now located. Or short:
This function sets the agent's assessment of the reward that he can receive by performing a certain action in a certain course. It also includes an assessment of what rewards an agent can receive in the future. The learning process is an iterative refinement of the value of the function Q on each move of the agent. The first step is to determine the value of the reward that the agent will receive this turn. Write it variable . Next, we define the maximum expected reward on subsequent turns:
Now it is necessary to decide that the agent has great value: immediate rewards or future ones. This problem is resolved by an additional factor in the component evaluation of subsequent awards. As a result, the value of the function Q predicted by the agent at this step should be as close as possible to the value:
Thus, the agent’s prediction error of the Q function value for the current move is written as follows:
We introduce a coefficient that will regulate the learning speed of the agent. Then the formula for the iterative calculation of the function Q has the form:
The general formula for the iterative calculation of the function Q:
Let us single out the main features that will make up the description of the environment from the point of view of the agent. The more extensive the set of parameters, the more accurate its response to changes in the environment. At the same time, the size of the state space can significantly affect the speed of learning.
Creating a class Q model. The variable gamma is the attenuation coefficient, which allows leveling the contribution of subsequent awards. The alpha variable is the coefficient of the model learning speed. The state variable is a dictionary of model states.
We'll get the agent status on this turn.
We train the model.
The method of obtaining awards. Agent is awarded a reward for continuing the simulation. The penalty is credited for colliding with the enemy.
Agent strategy Produces the best value selection from the model state dictionary. Agent class added variable eps, introducing an element of randomness when choosing a move. This is done to study the adjacent possible actions in this state.
Let us show what the agent managed to learn with the complete transfer of information about the simulation state (absolute coordinates of the agent, absolute coordinates of the enemy):
To begin, consider the situation when the agent does not receive any information about the environment at all.
As a result of the work of such an algorithm, the agent gains an average of 40-75 points per simulation. Training schedule:
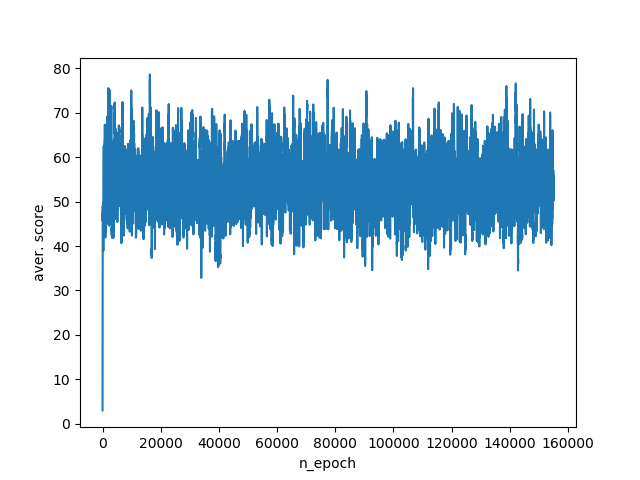
Add a data agent. First of all, you need to know how far the enemy is. We calculate this using the Euclidean distance. It is also important to have an idea how close the agent is to the edge.
Accounting for this information raises the agent's bottom figures by 20 points per simulation and its average score becomes between 60-100 points. Although the response to changes in the environment has improved, we still lose the lion’s share of the necessary data. So, the agent still does not know which way to move in order to break the distance with the enemy or move away from the edge of the edge. Training schedule:
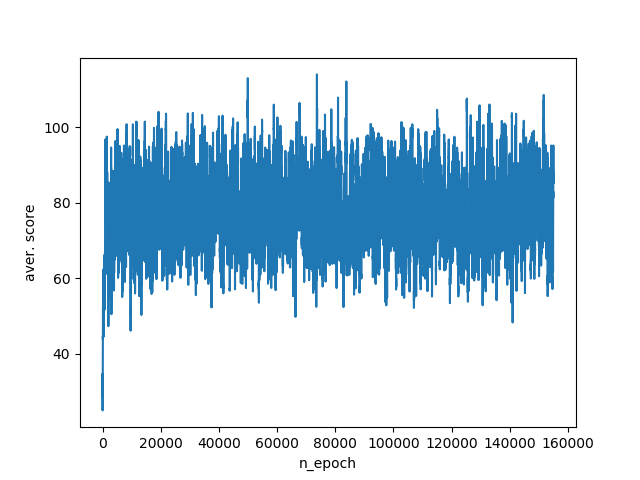
The next step is to add to the agent the knowledge of which side the enemy is located from, and also whether the agent is on the edge of the field or not.
Such a set of variables immediately raises the average number of points to 400-800. Training schedule:
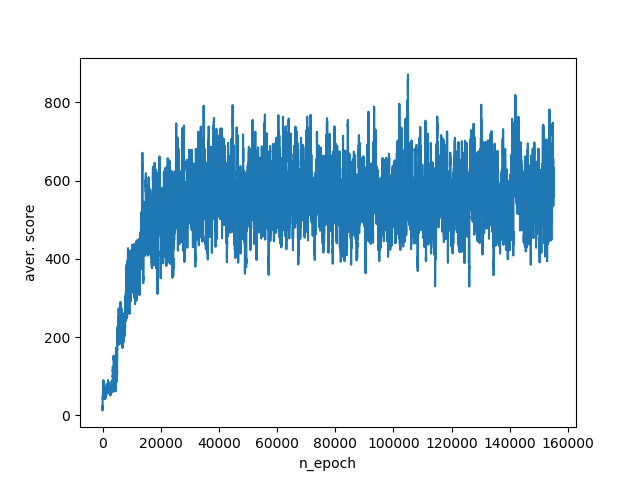
Finally, give the algorithm all the available information about the environment. Namely: the absolute coordinates of the agent and the enemy.
This set of parameters allows the agent to score 800-1400 points on test simulations. Training schedule:
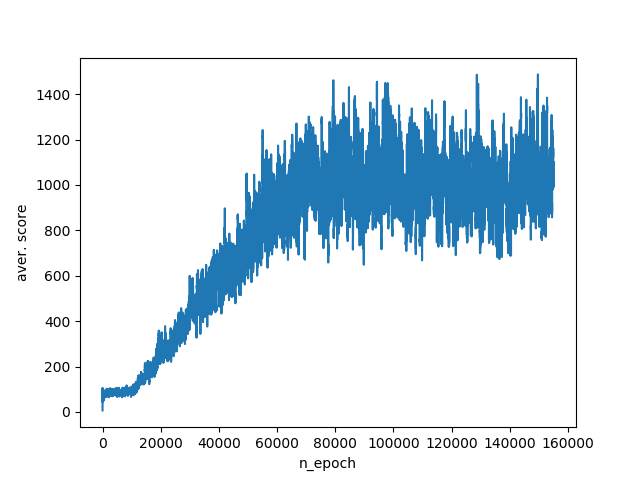
So, we reviewed the operation of the q-learning algorithm. Having twisted the parameters that are responsible for the perception of the environment by the agent, they clearly saw how an adequate transfer of information and taking all aspects into account when describing the environment affects the effectiveness of its actions. However, a complete description of the environment has a downside. Namely, the explosive growth of the space of states with increasing amount of information transmitted to the agent. To get around this problem, algorithms have been developed that approximate the state space, for example, the DQN algorithm.
Useful links:
habrahabr.ru/post/274597
ai.berkeley.edu/reinforcement.html
Full program code:
Part 1. Creating the environment
The medium in which the agent operates is represented by a two-dimensional field of size n. This is how it looks like:

')
Here the unit is represented by the agent, the deuce is marked with the opponent Now we turn directly to the code. Variables that describe the environment: field size, agent, list of opponents.
environment class
class W: def __init__(self,n): self.n=n self.P=P(1,1,n) self.ens=[EN(3,3,n),EN(4,4,n),EN(5,5,n)] Typical actor: agent or adversary.
actor class
class un: def __init__(self,x,y): self.x = x self.y = y def getxy(self): return self.x, self.y Agent description.
agent class
class P(un): def __init__(self,x,y,n): self.n=n un.__init__(self,x,y) The strategy of the agent, while empty.
agent strategy method
def strtg(self): return 0,0 Each of the participants in the simulation can make a move in any direction, including diagonally, the actor can also not move at all. The set of allowed movements on the example of the enemy:

Thanks to the diagonal movements, the enemy always has the opportunity to overtake the agent, no matter how hard he tries to leave. This provides a finite number of simulation moves for any degree of agent training. Let's write its possible actions with the validation of the offset. The method takes the change in the coordinates of the agent and updates its position
agent's move method
def move(self): dx,dy=self.strtg() a=self.x+dx b=self.y+dy expr=((0<=a<self.n) and (0<=b<self.n)) if expr: self.x=a self.y=b Description of the enemy.
adversary class
class EN(un): def __init__(self,x,y,n): self.n=n un.__init__(self,x,y) Moving an adversary with offset validation. The method does not exit the cycle until the condition of the course validity is satisfied.
opponent's move method
def move(self): expr=False while not expr: a=self.x+random.choice([-1,0,1]) b=self.y+random.choice([-1,0,1]) expr=((0<=a<self.n) and (0<=b<self.n)) if expr: self.x=a self.y=b One step simulation. Update the position of the enemy and the agent.
environment method, unfolds the next step of the simulation
def step(self): for i in self.ens: i.move() self.P.move() Visualization of the work of the simulation.
environment method, field drawing and position of actors
def pr(self): print('\n'*100) px,py=self.P.getxy() self.wmap=list([[0 for i in range(self.n)] for j in range(self.n)]) self.wmap[py][px]=1 for i in self.ens: ex,ey=i.getxy() self.wmap[ey][ex]=2 for i in self.wmap: print(i) Simulation, the main stages:
1. Registration of coordinates of actors.
2. Check the achievement of conditions for the completion of the simulation.
3. Start the update cycle of the simulation.
- Drawing environment.
- Update simulation state.
- Registration of coordinates of actors.
- Check the achievement of conditions for the completion of the simulation.
4. Drawing the environment.
environment method, simulation sequence playback
def play(self): px,py=self.P.getxy() bl=True for i in self.ens: ex,ey=i.getxy() bl=bl and (px,py)!=(ex,ey) iter=0 while bl: time.sleep(1) wr.pr() self.step() px,py=self.P.getxy() bl=True for i in self.ens: ex,ey=i.getxy() bl=bl and (px,py)!=(ex,ey) print((px,py),(ex,ey)) print('___') iter=iter+1 print(iter) Initialization of the environment and launch.
launch simulation
if __name__=="__main__": wr=W(7) wr.play() wr.pr() Part 2. Agent training
The q-learning method is based on the introduction of the Q function, reflecting the value of each possible agent action a for the current state s, in which the simulation is now located. Or short:
This function sets the agent's assessment of the reward that he can receive by performing a certain action in a certain course. It also includes an assessment of what rewards an agent can receive in the future. The learning process is an iterative refinement of the value of the function Q on each move of the agent. The first step is to determine the value of the reward that the agent will receive this turn. Write it variable . Next, we define the maximum expected reward on subsequent turns:
Now it is necessary to decide that the agent has great value: immediate rewards or future ones. This problem is resolved by an additional factor in the component evaluation of subsequent awards. As a result, the value of the function Q predicted by the agent at this step should be as close as possible to the value:
Thus, the agent’s prediction error of the Q function value for the current move is written as follows:
We introduce a coefficient that will regulate the learning speed of the agent. Then the formula for the iterative calculation of the function Q has the form:
The general formula for the iterative calculation of the function Q:
Let us single out the main features that will make up the description of the environment from the point of view of the agent. The more extensive the set of parameters, the more accurate its response to changes in the environment. At the same time, the size of the state space can significantly affect the speed of learning.
agent method, signs describing the state of the environment
def get_features(self,x,y): features=[] for i in self.ens: #800-1400 ex,ey=i.getxy() features.append(ex) features.append(ey) features.append(x) features.append(y) return features Creating a class Q model. The variable gamma is the attenuation coefficient, which allows leveling the contribution of subsequent awards. The alpha variable is the coefficient of the model learning speed. The state variable is a dictionary of model states.
class Q model
class Q: def __init__(self): self.gamma=0.95 self.alpha=0.05 self.state={} We'll get the agent status on this turn.
Q model method, on request, gets agent status
def get_wp(self,plr): self.plr=plr We train the model.
Q model method, one stage model training
def run_model(self,silent=1): self.plr.prev_state=self.plr.curr_state[:-2]+(self.plr.dx,self.plr.dy) self.plr.curr_state=tuple(self.plr.get_features(self.plr.x,self.plr.y))+( self.plr.dx,self.plr.dy) if not silent: print(self.plr.prev_state) print(self.plr.curr_state) r=self.plr.reward if self.plr.prev_state not in self.state: self.state[self.plr.prev_state]=0 nvec=[] for i in self.plr.actions: cstate=self.plr.curr_state[:-2]+(i[0],i[1]) if cstate not in self.state: self.state[cstate]=0 nvec.append(self.state[cstate]) nvec=max(nvec) self.state[self.plr.prev_state]=self.state[self.plr.prev_state]+self.alpha*(-self.state[self.plr.prev_state]+r+self.gamma*nvec) The method of obtaining awards. Agent is awarded a reward for continuing the simulation. The penalty is credited for colliding with the enemy.
environment method
def get_reward(self,end_bool): if end_bool: self.P.reward=1 else: self.P.reward=-1 Agent strategy Produces the best value selection from the model state dictionary. Agent class added variable eps, introducing an element of randomness when choosing a move. This is done to study the adjacent possible actions in this state.
agent method, next move selection
def strtg(self): if random.random()<self.eps: act=random.choice(self.actions) else: name1=tuple(self.get_features(self.x,self.y)) best=[(0,0),float('-inf')] for i in self.actions: namea=name1+(i[0],i[1]) if namea not in self.QM.state: self.QM.state[namea]=0 if best[1]<self.QM.state[namea]: best=[i,self.QM.state[namea]] act=best[0] return act Let us show what the agent managed to learn with the complete transfer of information about the simulation state (absolute coordinates of the agent, absolute coordinates of the enemy):
the result of the algorithm (gifka ~ 1Mb)
Part 3. We vary the parameters reflecting the state of the environment for the agent
To begin, consider the situation when the agent does not receive any information about the environment at all.
features 1
def get_features(self,x,y): features=[] return features As a result of the work of such an algorithm, the agent gains an average of 40-75 points per simulation. Training schedule:

Add a data agent. First of all, you need to know how far the enemy is. We calculate this using the Euclidean distance. It is also important to have an idea how close the agent is to the edge.
features 2
def get_features(self,x,y): features=[] for i in self.ens: ex,ey=i.getxy() dx=abs(x-ex) dy=abs(y-ey) l=hypot(dx,dy) features.append(l) to_brdr=min(x,y,self.n-1-x,self.n-1-y) features.append(to_brdr) return features Accounting for this information raises the agent's bottom figures by 20 points per simulation and its average score becomes between 60-100 points. Although the response to changes in the environment has improved, we still lose the lion’s share of the necessary data. So, the agent still does not know which way to move in order to break the distance with the enemy or move away from the edge of the edge. Training schedule:

The next step is to add to the agent the knowledge of which side the enemy is located from, and also whether the agent is on the edge of the field or not.
features 3
def get_features(self,x,y): features=[] for i in self.ens: ex,ey=i.getxy() features.append(x-ex) features.append(y-ey) # if near wall x & y. if x==0: features.append(-1) elif x==self.n-1: features.append(1) else: features.append(0) if y==0: features.append(-1) elif y==self.n-1: features.append(1) else: features.append(0) return features Such a set of variables immediately raises the average number of points to 400-800. Training schedule:

Finally, give the algorithm all the available information about the environment. Namely: the absolute coordinates of the agent and the enemy.
features 4
def get_features(self,x,y): features=[] for i in self.ens: ex,ey=i.getxy() features.append(ex) features.append(ey) features.append(x) features.append(y) return features This set of parameters allows the agent to score 800-1400 points on test simulations. Training schedule:

So, we reviewed the operation of the q-learning algorithm. Having twisted the parameters that are responsible for the perception of the environment by the agent, they clearly saw how an adequate transfer of information and taking all aspects into account when describing the environment affects the effectiveness of its actions. However, a complete description of the environment has a downside. Namely, the explosive growth of the space of states with increasing amount of information transmitted to the agent. To get around this problem, algorithms have been developed that approximate the state space, for example, the DQN algorithm.
Useful links:
habrahabr.ru/post/274597
ai.berkeley.edu/reinforcement.html
Full program code:
1. Basic environment model (from part 1)
import random import time class W: def __init__(self,n): self.n=n self.P=P(1,1,n) self.ens=[EN(3,3,n),EN(4,4,n),EN(5,5,n)] def step(self): for i in self.ens: i.move() self.P.move() def pr(self): print('\n'*100) px,py=self.P.getxy() self.wmap=list([[0 for i in range(self.n)] for j in range(self.n)]) self.wmap[py][px]=1 for i in self.ens: ex,ey=i.getxy() self.wmap[ey][ex]=2 for i in self.wmap: print(i) def play(self): px,py=self.P.getxy() bl=True for i in self.ens: ex,ey=i.getxy() bl=bl and (px,py)!=(ex,ey) iter=0 while bl: time.sleep(1) wr.pr() self.step() px,py=self.P.getxy() bl=True for i in self.ens: ex,ey=i.getxy() bl=bl and (px,py)!=(ex,ey) print((px,py),(ex,ey)) print('___') iter=iter+1 print(iter) class un: def __init__(self,x,y): self.x = x self.y = y def getxy(self): return self.x, self.y class P(un): def __init__(self,x,y,n): self.n=n un.__init__(self,x,y) def strtg(self): return 0,0 def move(self): dx,dy=self.strtg() a=self.x+dx b=self.y+dy expr=((0<=a<self.n) and (0<=b<self.n)) if expr: self.x=a self.y=b class EN(un): def __init__(self,x,y,n): self.n=n un.__init__(self,x,y) def move(self): expr=False while not expr: a=self.x+random.choice([-1,0,1]) b=self.y+random.choice([-1,0,1]) expr=((0<=a<self.n) and (0<=b<self.n)) if expr: self.x=a self.y=b if __name__=="__main__": wr=W(7) wr.play() wr.pr() 2. Environment model with agent training for 500 + 1500 simulations
import random import time from math import hypot,pi,cos,sin,sqrt,exp import plot_epoch class Q: def __init__(self): self.gamma=0.95 self.alpha=0.05 self.state={} def get_wp(self,plr): self.plr=plr def run_model(self,silent=1): self.plr.prev_state=self.plr.curr_state[:-2]+(self.plr.dx,self.plr.dy) self.plr.curr_state=tuple(self.plr.get_features(self.plr.x,self.plr.y))+(self.plr.dx,self.plr.dy) if not silent: print(self.plr.prev_state) print(self.plr.curr_state) r=self.plr.reward if self.plr.prev_state not in self.state: self.state[self.plr.prev_state]=0 nvec=[] for i in self.plr.actions: cstate=self.plr.curr_state[:-2]+(i[0],i[1]) if cstate not in self.state: self.state[cstate]=0 nvec.append(self.state[cstate]) nvec=max(nvec) self.state[self.plr.prev_state]=self.state[self.plr.prev_state]+self.alpha*( -self.state[self.plr.prev_state]+r+self.gamma*nvec) class un: def __init__(self,x,y): self.x = x self.y = y self.actions=[(0,0),(-1,-1),(0,-1),(1,-1),(-1,0), (1,0),(-1,1),(0,1),(1,1)] def getxy(self): return self.x, self.y class P(un): def __init__(self,x,y,n,ens,QM,wrld): self.wrld=wrld self.QM=QM self.ens=ens self.n=n self.dx=0 self.dy=0 self.eps=0.95 self.prev_state=tuple(self.get_features(x,y))+(self.dx,self.dy) self.curr_state=tuple(self.get_features(x,y))+(self.dx,self.dy) un.__init__(self,x,y) def get_features(self,x,y): features=[] # for i in self.ens: #80-100 # ex,ey=i.getxy() # dx=abs(x-ex) # dy=abs(y-ey) # l=hypot(dx,dy) # features.append(l) # to_brdr=min(x,y,self.n-1-x,self.n-1-y) # features.append(to_brdr) for i in self.ens: #800-1400 ex,ey=i.getxy() features.append(ex) features.append(ey) features.append(x) features.append(y) # for i in self.ens: #800-1400 # ex,ey=i.getxy() # features.append(x-ex) # features.append(y-ey) # features.append(self.n-1-x) # features.append(self.n-1-y) # for i in self.ens: #400-800 # ex,ey=i.getxy() # features.append(x-ex) # features.append(y-ey) # # if near wall x & y. # if x==0: # features.append(-1) # elif x==self.n-1: # features.append(1) # else: # features.append(0) # if y==0: # features.append(-1) # elif y==self.n-1: # features.append(1) # else: # features.append(0) # features=[] #40-80 return features def strtg(self): if random.random()<self.eps: act=random.choice(self.actions) else: name1=tuple(self.get_features(self.x,self.y)) best=[(0,0),float('-inf')] for i in self.actions: namea=name1+(i[0],i[1]) if namea not in self.QM.state: self.QM.state[namea]=0 if best[1]<self.QM.state[namea]: best=[i,self.QM.state[namea]] act=best[0] return act def move(self): self.dx,self.dy=self.strtg() a=self.x+self.dx b=self.y+self.dy expr=((0<=a<self.n) and (0<=b<self.n)) if expr: self.x=a self.y=b class EN(un): def __init__(self,x,y,n): self.n=n un.__init__(self,x,y) def move(self): expr=False cou=0 while not expr: act=random.choice(self.actions) a=self.x+act[0] b=self.y+act[1] expr=((0<=a<self.n) and (0<=b<self.n)) if expr: self.x=a self.y=b class W: def __init__(self,n,QModel): self.ens=[EN(n-2,n-2,n)]#,EN(n-2,n-1,n),EN(n-1,n-2,n),EN(n-1,n-1,n)] self.P=P(1,1,n,self.ens,QModel,self) self.n=n self.QM=QModel self.QM.get_wp(self.P) def step(self): self.P.move() for i in self.ens: i.move() def pr(self,silent=1): """print map""" #print('\n'*100) px,py=self.P.getxy() self.wmap=list([[0 for i in range(self.n)] for j in range(self.n)]) self.wmap[py][px]=1 for i in self.ens: ex,ey=i.getxy() self.wmap[ey][ex]=2 if not silent: for i in self.wmap: print(i) def is_finished(self): px,py=self.P.getxy() end_bool=True for i in self.ens: ex,ey=i.getxy() end_bool=end_bool and ((px,py)!=(ex,ey)) return end_bool def get_reward(self,end_bool): if end_bool: self.P.reward=1 else: self.P.reward=-1 def play(self,silent=1,silent_run=1): end_bool=self.is_finished() iter=0 while end_bool: self.pr(silent) self.step() end_bool=self.is_finished() self.get_reward(end_bool) if silent_run: self.QM.run_model(silent) if not silent: print('___') time.sleep(0.1) iter=iter+1 return iter QModel=Q() plot=plot_epoch.epoch_graph() for i in range(500): wr=W(5,QModel) wr.P.eps=0.90 iter=wr.play(1) wr.pr(1) plot.plt_virt_game(W,QModel) for i in range(1500): wr=W(5,QModel) #print(len(QModel.state)) wr.P.eps=0.2 iter=wr.play(1) wr.pr(1) plot.plt_virt_game(W,QModel) plot.plot_graph() print('___') for i in range(10): wr=W(5,QModel) wr.P.eps=0.0 iter=wr.play(0) wr.pr(0) 3. Plotting module (plot_epoch.py).
import matplotlib.pyplot as plt class epoch_graph: def __init__(self): self.it=0 self.iter=[] self.number=[] self.iter_aver=[] def plt_append(self,iter): self.it=self.it+1 self.iter.append(iter) self.number.append(self.it) if len(self.iter)>100: self.iter_aver.append(sum(self.iter[-100:])/100) else: self.iter_aver.append(sum(self.iter)/len(self.iter)) def plt_virt_game(self,W,QModel): wr=W(5,QModel) wr.P.eps=0.0 iter=wr.play(1,0) self.plt_append(iter) def plot_graph(self): plt.plot(self.number,self.iter_aver) plt.xlabel('n_epoch') plt.ylabel('aver. score') plt.show() Source: https://habr.com/ru/post/345656/
All Articles