Methods of simulation of probability distributions in the programming language Python
In this article, we consider simulation methods based on the theory of queuing systems, in which elements of mathematical statistics and probability theory are widely used. The purpose of this article is to develop methods that can be used to create models based on probability distributions and elements of mass servicing.
Before proceeding with the development of methods, we define the key approaches that we will use in the process: the generation of random variables, probability distributions, as well as some elements of probability theory and mathematical statistics. In the results of the experiments we will see an experimental demonstration of the behavior of probability distributions and imitation of random processes. All this will give us an instrumental basis for creating various simulation models in which probability distributions appear.
All modeling methods for this study are presented in the Python programming language. This language is a common tool in research and teaching.
')
In the next stages of the study, which will be presented in future articles, we turn to more complex experiments: consider probability distributions that are not included in the scope of this article, consider simulation modeling of systems and queuing networks, and also demonstrate programming similar models using parallel computing.
Consider simple models for throwing one or more dice. Modeling will start with the generation of random numbers. The task of generating numbers and questions about true and quasi-randomness are not included in our research, but you can find these discussions in other sources. Our models use a Python pseudo-random variable generator. At the initial stage, for clarity of study, it is possible to increase the number of tests by observing the result of the simulation.
Let's start with the generation of random variables. Methods for generating them boil down to using standard Python libraries.
The random module from the standard library provides the ability to obtain random real numbers in the range from 0 to 1, random integers in a given range, random selection of sequence elements, and much more:
The random module can be used, for example, to shuffle a deck of cards in a game, to randomly select an image in a slideshow program, in statistical modeling programs, and so on. For more information, refer to the standard Python library library manual.
The NumPy extension, which contains the implementation of mathematical calculations for Python by combining compiled and optimized extension libraries with the Python language NumPy, turns Python into a powerful, efficient and convenient tool for mathematical calculations.
A detailed description of the NumPy module can be found in the official documentation for this package.
We proceed to the simulation: we will throw a dice. Below is a listing of programming the model of throwing one cube (Fig. 1). The cube can take one of six values.
Fig.1. Listing of programming a single die toss model
In the presented program we set the number of tests: how many times the die is thrown, and the array: what value falls in each test. The result is displayed in the form of a histogram (Fig. 2).
Considering the result, we can assume that the distribution is uniform. By increasing the number of tests up to 10,000 times, you can see that the histogram has a form similar to a uniform distribution histogram.
The following test will consider the model of throwing two dice. The program code is slightly changed (Fig. 3).

Fig.2. Simulation results of one die toss
Fig.3. Part of the modified listing for programming the model of throwing two dice
In the presented listing, a significant change is the assignment of the value to the array, in which we write the dropped values of two cubes already. The second change, less significant, is the representation of the histogram of the corresponding value options. The result of the program is shown in Fig.4.
Having obtained the result of modeling the tossing of two cubes, we consider the problem of modeling the normal (Gauss) distribution and how far it correlates with the task of modeling the tossing of several cubes. The program code also changes insignificantly: only one line of assigning values to the array changes (Fig. 5).
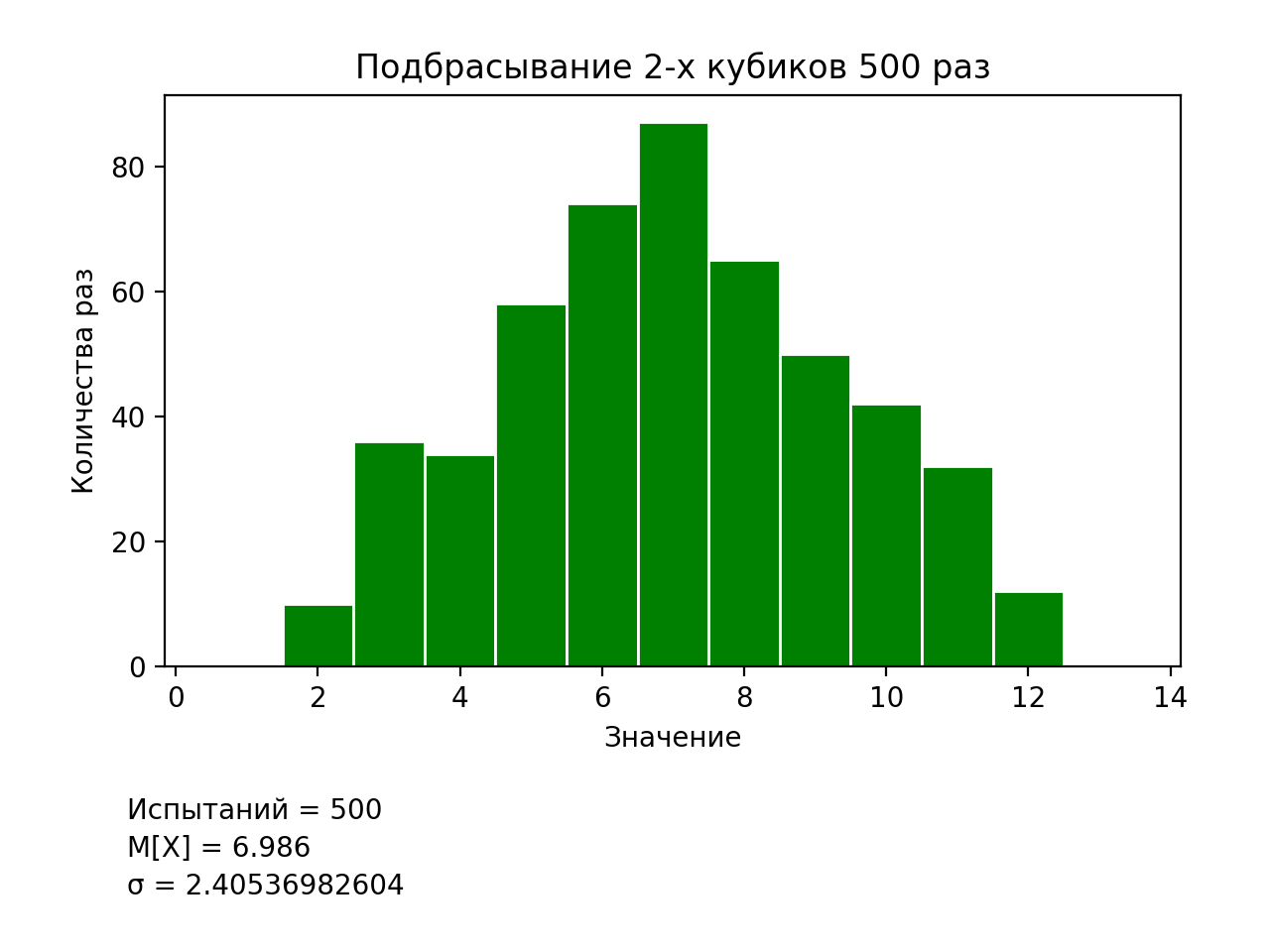
Fig.4. Simulation results of throwing two dice
Fig.5. Part of the modified listing for programming the normal distribution model
In the presented listing, the normalvariate library random method is used that generates values with a normal probability distribution with the mu and sigma parameters, which are the mean and the standard deviation of the distribution, respectively. The result of the program is shown in Fig.6.
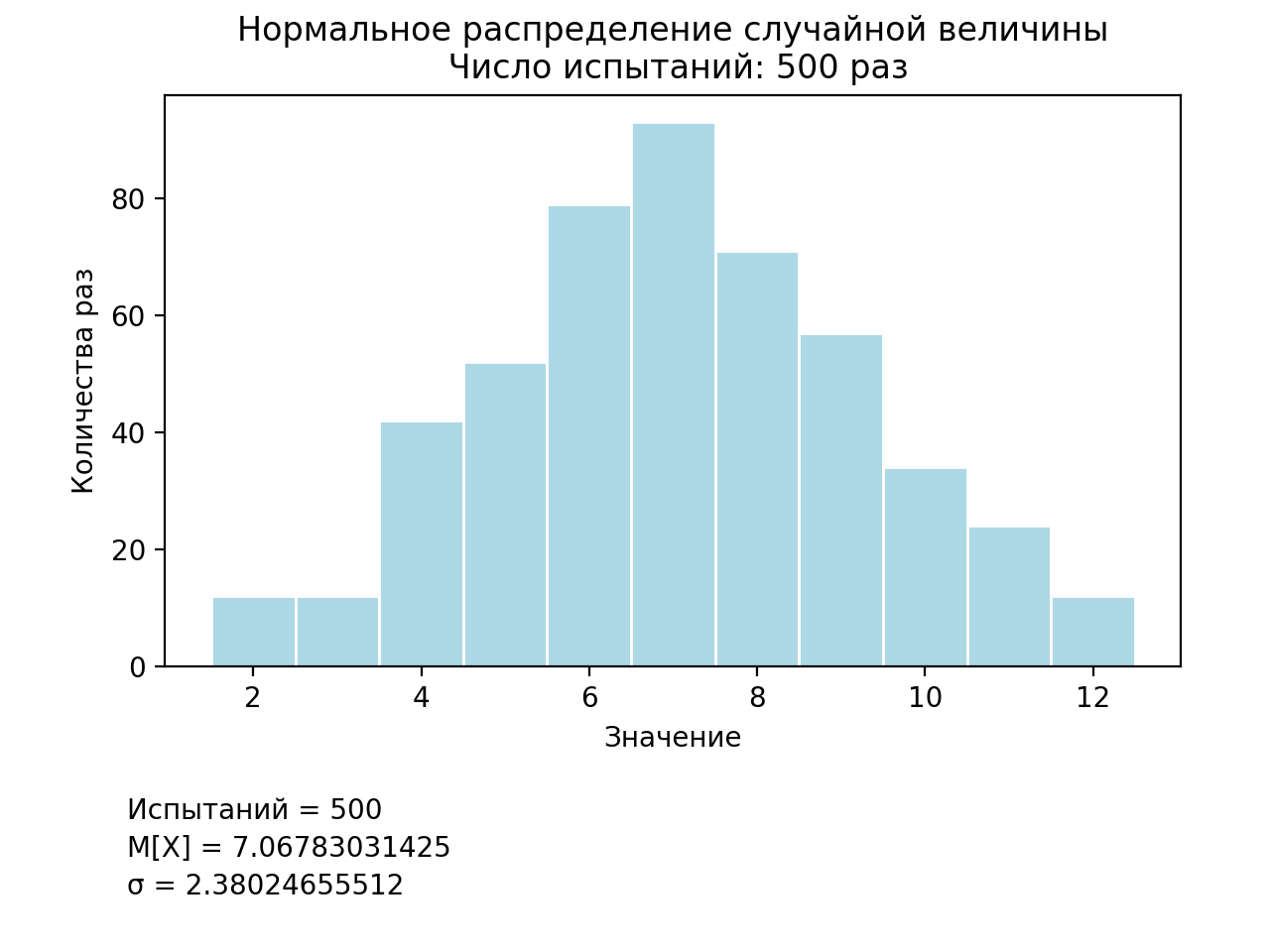
Fig.6. Normal distribution simulation results
The final step is to model the exponential distribution. Exponential distribution is often used in modeling the distribution (duration) of the intervals between the moments of receipt of requests in queuing systems of different types. The listing also differs slightly from the other program listings presented in our study (Fig. 7).
The result of the simulation is shown in Fig.8.
Fig.7. Part of a modified listing for programming an exponential distribution model
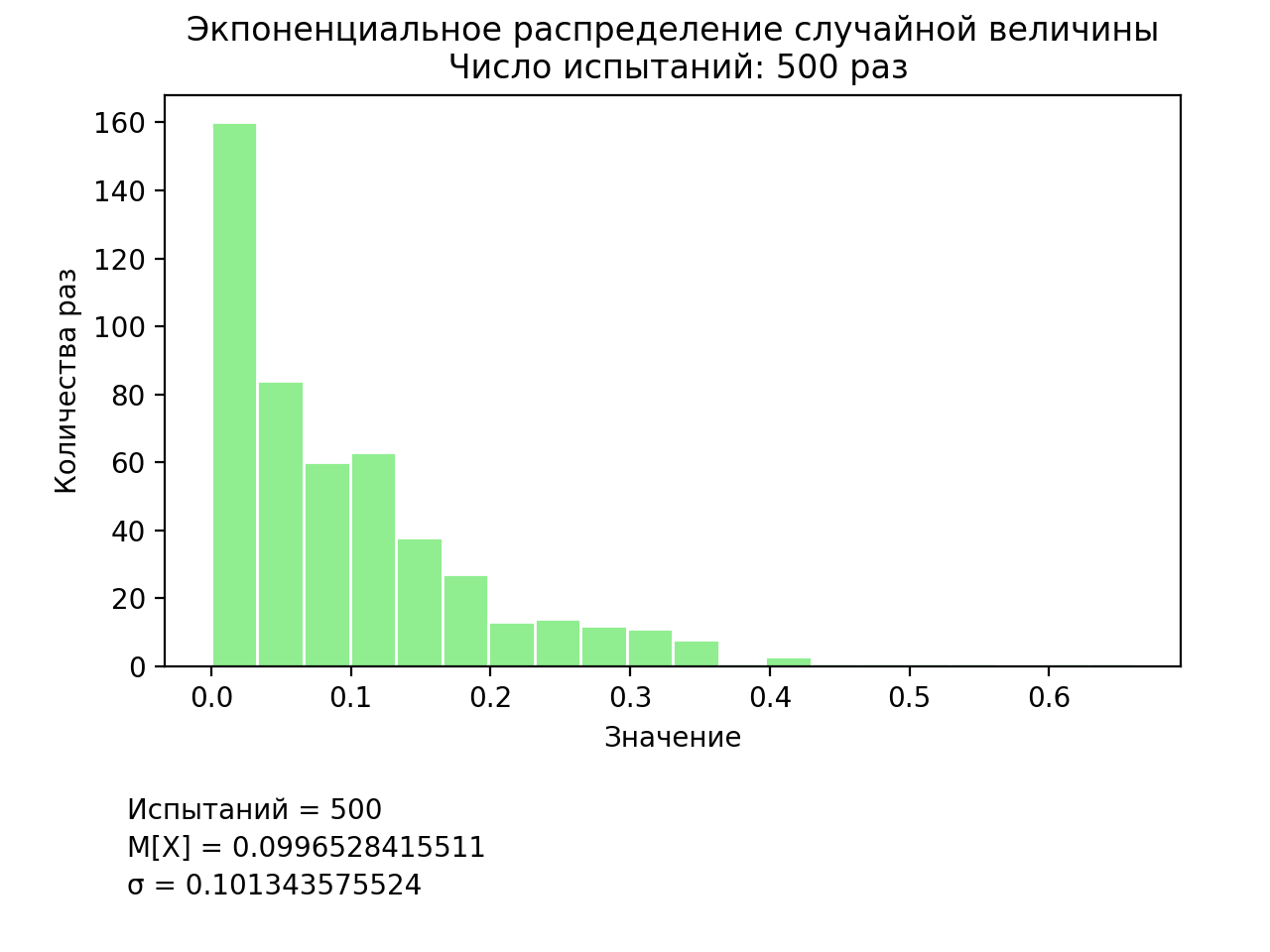
Fig.8. Exponential Distribution Simulation Results
In this article, several software implementations of the probability distribution model in Python were considered. These models provide the basis for conducting their own experiments and research.
At this stage, only some of the methods and approaches are presented, and in the future, the author will present additional methods for modeling using probability distributions, the Python programming language and queuing theory.
Before proceeding with the development of methods, we define the key approaches that we will use in the process: the generation of random variables, probability distributions, as well as some elements of probability theory and mathematical statistics. In the results of the experiments we will see an experimental demonstration of the behavior of probability distributions and imitation of random processes. All this will give us an instrumental basis for creating various simulation models in which probability distributions appear.
All modeling methods for this study are presented in the Python programming language. This language is a common tool in research and teaching.
')
In the next stages of the study, which will be presented in future articles, we turn to more complex experiments: consider probability distributions that are not included in the scope of this article, consider simulation modeling of systems and queuing networks, and also demonstrate programming similar models using parallel computing.
Methods for modeling random variables and python random number generators
Consider simple models for throwing one or more dice. Modeling will start with the generation of random numbers. The task of generating numbers and questions about true and quasi-randomness are not included in our research, but you can find these discussions in other sources. Our models use a Python pseudo-random variable generator. At the initial stage, for clarity of study, it is possible to increase the number of tests by observing the result of the simulation.
Let's start with the generation of random variables. Methods for generating them boil down to using standard Python libraries.
The random module from the standard library provides the ability to obtain random real numbers in the range from 0 to 1, random integers in a given range, random selection of sequence elements, and much more:
The random module can be used, for example, to shuffle a deck of cards in a game, to randomly select an image in a slideshow program, in statistical modeling programs, and so on. For more information, refer to the standard Python library library manual.
The NumPy extension, which contains the implementation of mathematical calculations for Python by combining compiled and optimized extension libraries with the Python language NumPy, turns Python into a powerful, efficient and convenient tool for mathematical calculations.
A detailed description of the NumPy module can be found in the official documentation for this package.
Methods for modeling probability distributions using python
We proceed to the simulation: we will throw a dice. Below is a listing of programming the model of throwing one cube (Fig. 1). The cube can take one of six values.
import pylab import numpy # trials = 500 # values = numpy.random.randint(1, 7, size=trials) pylab.hist(values, bins=[0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5], edgecolor='white') pylab.xlabel('') pylab.ylabel(' ') pylab.title(' ' + str(trials) + ' ') pylab.show() Fig.1. Listing of programming a single die toss model
In the presented program we set the number of tests: how many times the die is thrown, and the array: what value falls in each test. The result is displayed in the form of a histogram (Fig. 2).
Considering the result, we can assume that the distribution is uniform. By increasing the number of tests up to 10,000 times, you can see that the histogram has a form similar to a uniform distribution histogram.
The following test will consider the model of throwing two dice. The program code is slightly changed (Fig. 3).

Fig.2. Simulation results of one die toss
... # values = [] for i in range(trials): values.append(numpy.random.randint(1, 7) + numpy.random.randint(1, 7)) pylab.hist(values, bins=[0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5, 9.5, 10.5, 11.5, 12.5, 13.5], facecolor='green', edgecolor='white') ... Fig.3. Part of the modified listing for programming the model of throwing two dice
In the presented listing, a significant change is the assignment of the value to the array, in which we write the dropped values of two cubes already. The second change, less significant, is the representation of the histogram of the corresponding value options. The result of the program is shown in Fig.4.
Having obtained the result of modeling the tossing of two cubes, we consider the problem of modeling the normal (Gauss) distribution and how far it correlates with the task of modeling the tossing of several cubes. The program code also changes insignificantly: only one line of assigning values to the array changes (Fig. 5).

Fig.4. Simulation results of throwing two dice
... # values = [] for i in range(trials): mu = 7 sigma = 2.4 values.append(random.normalvariate(mu, sigma)) ... Fig.5. Part of the modified listing for programming the normal distribution model
In the presented listing, the normalvariate library random method is used that generates values with a normal probability distribution with the mu and sigma parameters, which are the mean and the standard deviation of the distribution, respectively. The result of the program is shown in Fig.6.

Fig.6. Normal distribution simulation results
The final step is to model the exponential distribution. Exponential distribution is often used in modeling the distribution (duration) of the intervals between the moments of receipt of requests in queuing systems of different types. The listing also differs slightly from the other program listings presented in our study (Fig. 7).
The result of the simulation is shown in Fig.8.
... lambd = 10 # values = [] for i in range(trials): values.append(random.expovariate(lambd)) pylab.hist(values, 20, facecolor='lightgreen', edgecolor='white') ... Fig.7. Part of a modified listing for programming an exponential distribution model

Fig.8. Exponential Distribution Simulation Results
Conclusion
In this article, several software implementations of the probability distribution model in Python were considered. These models provide the basis for conducting their own experiments and research.
At this stage, only some of the methods and approaches are presented, and in the future, the author will present additional methods for modeling using probability distributions, the Python programming language and queuing theory.
Source: https://habr.com/ru/post/345392/
All Articles