Nebraska problem

Casey Muratori is one of the programmers for The Witness. In the process of developing the game, he published in his blog posts about technical problems that stood before him. Below is a translation of one of these posts.

Throughout my career as a programmer, one principle remained unchanged: I always take the time to ask myself - why am I doing something exactly as I do? This has always happened, from the creation of simple software constructs to high-level algorithms. Even deep-rooted ideas are often mistaken, and by subjecting these ideas to doubts, we can come to surprising and important discoveries.

Therefore, when I work on something, I reflexively begin to consider the reasons behind it. And planting grass, too, was no exception.
')
The code I described last week is already embedded in The Witness source tree, along with many other non-related grass system modifications, which I will discuss next week. It was a reasonable solution to the obvious problem, and time was running out, so I knew that then it was not up to the solution of deeper issues. But in my head I made a mental note that the next time I work on the generation of patterns, I need to ask the question "why." Thanks to the time allotted for writing this article, I got this opportunity.

The question “why” in this case is quite simple: why do we use blue noise to place the grass?

Blue noise is a great noise pattern. As I mentioned in the first article about grass, he has nice looking properties. But when I changed the grass system The Witness to more effectively create blue noise, I simply repeated after the one who wrote the code initially. But who said he made a good decision by choosing a blue noise? What task exactly did he want to solve, and was the blue noise the best solution? In the past, I used blue noise for things like grass, but was I sure that under current conditions it would be the best location strategy?

When I wrote the previous two articles and the code that was used to generate these schemes, I realized that the answers to these questions most likely are “no”. I hinted at this in the previous article, when I said that our approach has a theoretical problem, and now I can clearly say what this problem is, and then return to the attempts of its solution.

Rows of corn

Here are a few screenshots of the patterns created by the original techniques of rough searching and sampling of the neighbors, which I discussed earlier:


Here is how these patterns look from the point of view of a regular player:


And here, finally, what the patterns look like, at each point of which flora billboards are located:


As you can see, there is not much difference between them, that is, we did a good job and created a brute force algorithm that can work quite quickly in The Witness . But if you look at these screenshots a little longer, you can see that it is a bit difficult to understand how generally blue noise is good. In fact, I have no idea how bad or good these patterns are. We have no starting point from which we could compare such images. How can you tell how good the pattern is without some well-known scheme that creates better results?

Intuitively, it seemed to me that the blue noise effectively covers the space. At a higher level, the grass distribution task can be formulated as “using the minimum number of points to create a visually pleasing coverage of the desired area”. I say “the minimum number of points” because, as in the case of any other real-time rendering task, the fewer points you need to adequately cover the space visually, the lower the costs for rendering grass in each frame. The lower the cost, the more power the graphics system has to render other things. And in The Witness there are a lot of other things that need to be rendered in each frame, believe me.

Therefore, yes, if I didn’t like filling in some places, I could always be able to increase the density of blue noise by spending more rendering power, but getting a more dense coverage:


But it is obvious that you need to strive for the lowest possible density, and at the same time create a convincing coverage, so I understood that the required level should be similar to the first screenshots of the article. Without an excessive amount of points, it may not be possible to avoid empty spots near the player, but a little further away from him the ideal pattern will make the grass beautiful and rich.

However, when I experimented with patterns last week, I noticed a very unpleasant thing. In the same pattern, when the camera is rotated at certain points, parts of the pattern create almost even rows, and obvious voids are noticeable even far from the camera, where ideally there should be enough vegetation overlapping each other:


This is noticeable when using both techniques, so it is similar to the property of blue noise in general, or at least all kinds of blue noise generated by the Poisson spot method.

For reasons that I will not reveal now, I had to spend some time sitting in the back seat of a car in Nebraska, traveling along the most boring freeway in the world (almost any way in Nebraska can be called that). If you look at the corn fields from the window, you will notice that the rows of corn have the same property: from a variety of angles they look like corn fields, but looking at the right angle, we will see that they suddenly become very repetitive. Long and narrow gaps between the rows are visible. This is quite normal for a corn field, but not quite well when you need to create the illusion of densely growing grass.

Because of the similarity to this property of the corn field, I called this problem with blue noise "the Nebraska problem."

I did not want the Nebraska problem to interfere with the distribution of grass. As far as I know, this is a theoretical problem, because there is nothing wrong with the blue noise algorithms themselves. In this case, the practice is absolutely correct, only theory is inadequate.

Since I did not know the theory of noise that could cope with this problem and did not even encounter articles that would mention its existence, I decided to experiment with breaking the rules of blue noise to see if I could solve the Nebraska problem on my own.

Experimenting with packing factor

Every time I start researching a new task, I don’t have a clear idea about it. I understand that the problem exists, but it has not yet been specifically defined, so I randomly try obvious things.

The first thing I tried was to change the way the points were selected by the neighbor selection algorithm. In the previous article, I did not go into details of how this algorithm selects the points to be checked. I simply made it take a random point “from r to 2r” in a random direction from the base point.

This can be done in different ways. The simplest is to uniformly choose the angle and distance in the range from r to 2r and use them directly. But if you apply the points selected in this way, you can see that they have a noticeable deviation to the center of the circle:


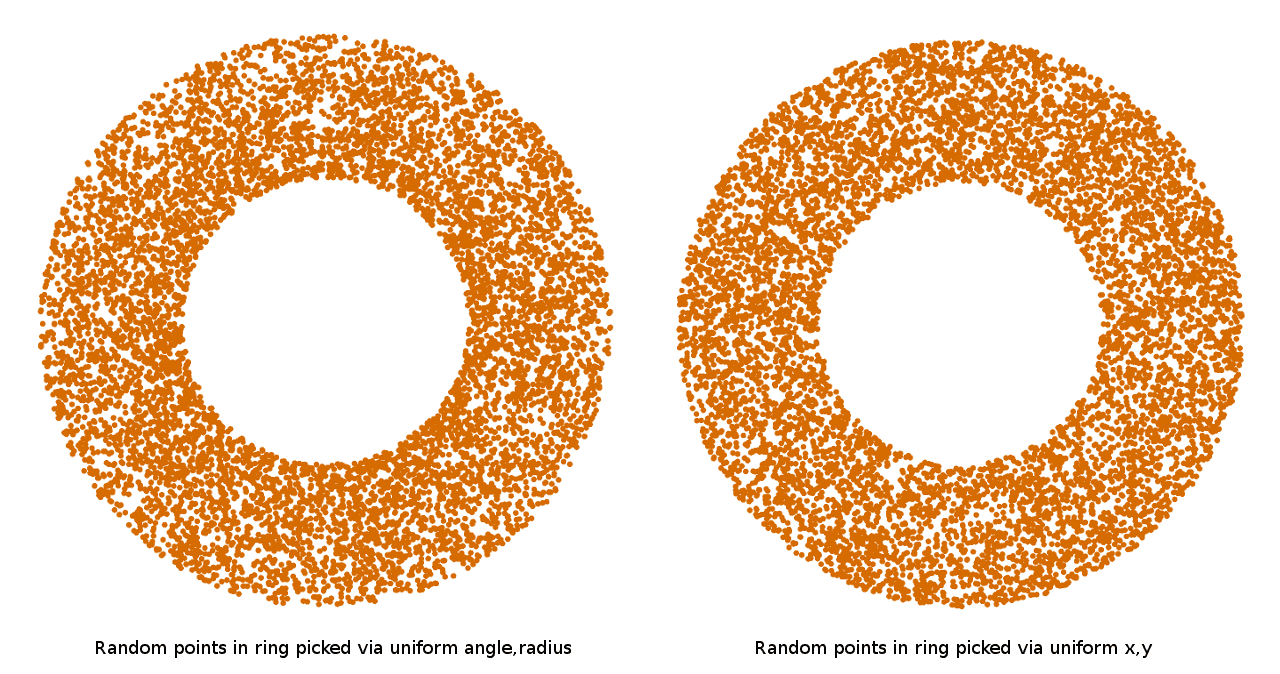
What's going on here? If you think about it, it becomes clear that the larger the radius of the circle, the farther the point on the circle moves as the angle changes. This means that to cover the perimeter of large circles with the same Euclidean density of random points, we need to take more random angles than when covering small circles. That is, if we uniformly take a random angle and a random radius, then as a result, smaller radii will always be covered more densely than large ones. To really select points with a uniform density inside a circle, it is necessary either to select an angle and radius not uniformly to take into account the changing influence of the angle as the radius increases, or, more simply, you can simply select points in a square and discard those that do not fall into a circle.

Well, so why am I talking about this? When implementing the algorithm of selection of neighbors, I usually leave the bias when approaching the center. It turns out faster, and it turned out that visually it does not affect the finished pattern. But since my task was to change the pattern, I had to think - what if forcing a sample of points to be even more biased?

Therefore, I decided to introduce the concept of "packing ratio". Instead of selecting points in the gap at a distance from r to 2r from the base point, I made the parameter equal to 2. Thus, I can force all selected points to be closer to the base points, theoretically reducing the average distance of the pattern and creating a denser packing:


Unfortunately, this attempt quickly proved its fruitlessness, because the dense packaging emphasized the Nebraska problem even more. If you look at the patterns, you can understand this: when the packaging becomes more dense, the probability that the two “branches” of the neighbors selection algorithm will run parallel to each other increases without the possibility of creating more stochastic patterns that dilute the empty space in between.

Consider spaces

So, experiments with packaging turned out to be unproductive and it was logical. I began to think that it might not be enough to allow the points to be placed more flexibly in spaces that are not filled tightly. Perhaps, if I make a second pass over the original blue noise pattern with a looser placement radius, I can fill the places where the aligned rows create noticeable gaps:


It turned out that it actually works. At least, it seemed so at first glance. But when I counted the number of points, I realized that in fact if you simply create a blue noise pattern with the same number of points as when filling in the gaps, it will also be quite dense and will not allow you to avoid the problem:


That is, although the elimination of gaps in the original pattern can bear fruit, I could immediately see how to make this method work efficiently: in fact, it increased the number of points, and did not eliminate the problem with the distribution of existing points.

We plant grass along the lines

Having failed with a few modifications of blue noise, I began to try more ridiculous approaches that didn’t have blue noise properties at all, just to check if there was something interesting. Returning to the first concepts, I thought: so, if my goal is to avoid lines of sight with spaces, then it may be worthwhile to generate a pattern based on this principle. Therefore, I wrote an algorithm that selected random lines of sight in the field. He passed along each of the lines and searched for the lengths of the lines along which a certain distance traveled, without meeting points:


Unfortunately, since the algorithm selects random lines, it may well choose two lines right next to each other, which again brings us back to the Nebraska problem. In some parts of the pattern, it works quite well, but in those parts where the lines are approximately parallel, the Nebraska problem manifests itself in full force.

Selective deletion

Similar to the previous method, I thought that it might be worth trying the opposite approach: start with dense coverage of the area generated by white noise, and then remove only those points that do not exactly create long continuous lines of empty space. Each point had to be checked with a large number of directions, and the algorithm determined where the first “hit” occurred along these lines in the forward and reverse directions. If the distance along all the tested lines was small, then I deleted this point. If the resulting distance along any of these lines is too large, then I left a point:


Unfortunately, it gave results similar to the previous attempt: when setting the parameters in one way, the Nebraska problem disappeared, but the sampling was too dense. With a different setting of the parameters, the sampling turned out to be too sparse and noticeable gaps appeared everywhere, even if I deliberately tried to avoid the Nebraska problem.

At that moment I should have known. what happens but this did not happen. It is worth considering that most likely it was in the middle of Wednesday and I realized that I would never have time before my deadline for Witness , so I started to get a little nervous. I think not clearly enough. What should I do? Should I keep pushing or just call and say: “well, I have a problem with the algorithm, and damn if I know how to solve it. Have a nice environment. CHRISTMAS CANCELED! ”.

I know how important Santa Claus is to you all. It is not every day that the fat, constantly smiling bearded grandfather secretly penetrates the house and leaves “presents” for your children, whom he has “watched” all year. Would you really like to be the person who canceled Christmas?

No, of course not, and I decided - Christmas cannot be canceled. Christmas is not canceled. CHRISTMAS JUST A LIGHTLY POSTPONING.

Relaxation

So, well, no problem. Christmas is postponed. It was Wednesday, so it may take place on Thursday. Or on Friday. Back to work.

If you read articles on graphics research, you probably agree with what I will say: if people get into a situation where the algorithm obviously simply does not work, then you should definitely relax. Can't arrange the points where they are needed? Relax! If you can't find a way to put points where they are needed, let them figure it out for yourself.

Therefore, I added a relaxation phase. And I tried to use two different “energy functions” for relaxation, the first of which was a simple version of “chase away other points”:


The second was a version of “break adjacent lines”: she searched for sets of three or more points that are approximately on the same line, and tried to move one of the internal points in the direction from which there was more open space:


As you can see from the illustrations, none of these strategies looked promising. Although they were completely situational and I could tune it in order to get better results, I did not see anything in the preliminary results that would mean a big sense in relaxation strategies. It seemed that no matter how I tried to move the points, they as a result randomly created new corn rows, even if I broke old ones, or the gaps between them turned out to be too large, which was even worse.

It was Wednesday night, and it was dinner time. But it was an unusual environment, so the dinner, too, was supposed to be unusual. In fact, it was Crazy Wednesday, that is, it was time for a mad dinner on Wednesday.

Directional restrictions

Crazy Wednesday is a special day of the week (often they don't even happen on Wednesdays, but I won't say why) when Shaun Barrett , Fabien Guisin , Jeff Roberts and I are going to have a completely insane time: four programmers are sitting around a table restaurant and within an hour discuss the details of a specific technical problem. And if this sounds insanely not enough for you, then specifically on that Insane Wednesday we had a special guest - Tommy Refenes , so I knew that she would be even Crazier than before.

A visit to Mad Environment will be useful, because I can discuss the problem with other guys, and maybe I will have a fresh look. So it happened.

After I explained the problem to them, Fabien and Sean came to the conclusion that first of all it was best to prevent the original neighbor selection algorithm from creating lines, thus avoiding the task of correcting the pattern. If the original random generation algorithm does not create rows, then as a result, patterns can be obtained better than after correcting rows after the process, because eliminating rows is a global problem: you need to move points so that the pattern can change dramatically with this change. If you do not create rows initially, then the entire pattern will be rowless, that is, the global problem simply disappears.

Therefore, I tried heuristics to prevent the creation of lines, for example, making so that each new point would never be along the same line as the previous one:


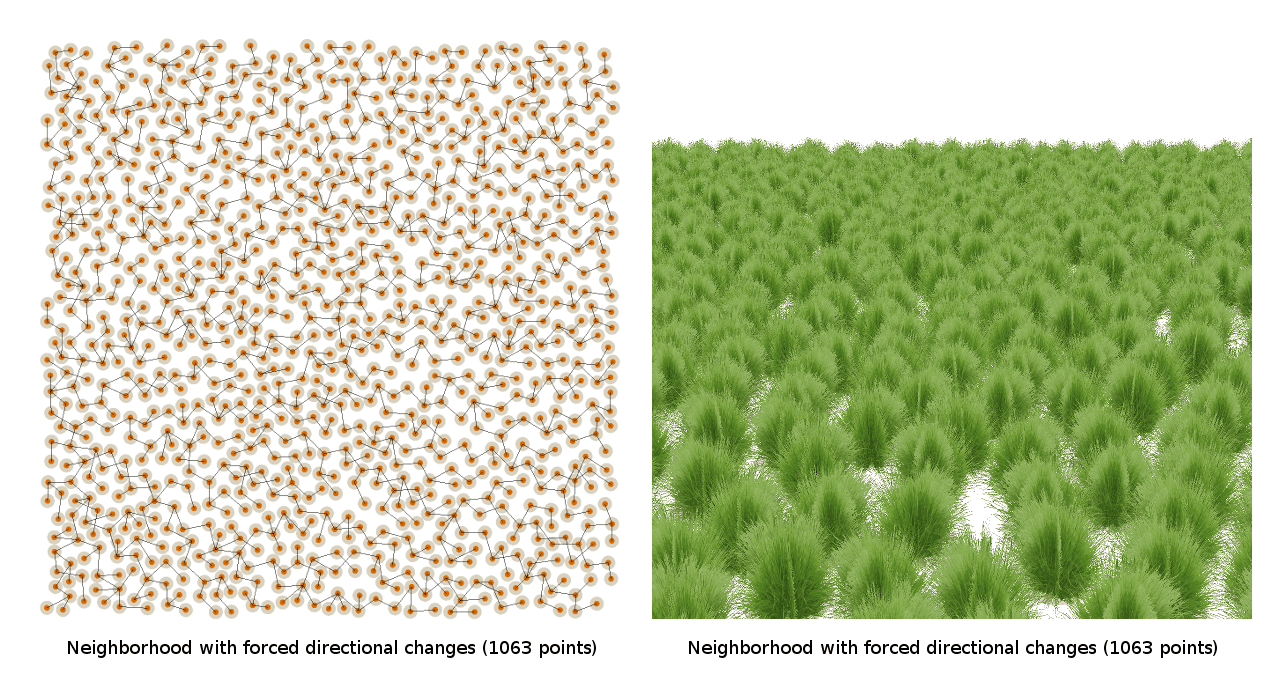
Unfortunately, I still got the Nebraska problem. Even no direct branch of the neighbor selection algorithm created rows, it seems that the neighboring branches were conspiring with each other and still creating rows!

It was already starting to get ridiculous. How is it that each algorithm produces the same artifact? What's happening?

Twisted Hex Pack

Although I was still not overwhelmed by a serious insight, I began to understand what the error was. I took a step back and thought about what might be necessary to create a pattern without corn rows that would not use too many points. I began to come to the conclusion that I really needed curves. I wanted to make the generated lines always give bends to points, because the two curves of a number of points are the pattern in which linear gaps will never be seen. Any random arrangement can actually create the mutual influence of points, creating adjacent lines, even on each side of just three points - this is enough to show the Nebraska problem. Therefore, an algorithm that creates a guaranteed absence of gaps may not be random at all, but is constant.

This completely changed my approach to the problem. All this time I thought that for a good coverage accident is obligatory. But now, after careful consideration of the problem, it seemed to me that an accident could actually be bad.

Therefore, I began to think about repeating patterns that may have the properties I need. They should have looked not obvious when viewed from the point of view of an ordinary player (standing on the grass). They should not contain continuous straight lines of points. They must effectively cover the space.

I knew that hexagonal packings had the most dense packing for circles:


Therefore, I decided that if we need to effectively cover the space, then it is probably best to start with hexagonal packaging, because it will position each point at a distance that is visually optimal for coverage, while minimizing the number of points used.

But hexagon packs themselves are obviously terrible, because these are corn rows in different directions, that is, not at all what I need. So I thought - what if I twist the hex wrap? I tried to interpret the hexagon packing in polar coordinates in order to get curved rows of rows:


I also tried various turn patterns, similar to the original neighbor selection algorithm, in which I branched out new points in a hexagon pattern, which were turned randomly or permanently.

Unfortunately, the hex packs also did not work. They either left gaps, or created crowding, or made lines in one of the directions. But, fortunately, it was they who opened my eyes to what exactly my goal is.

See - distribution is performed on the plane. There are always two orthogonal bases on the plane. Therefore, using one axis of curvature, which I applied for curving hex packing with polar coordinates, would never fit: I would bend one of the axes along which lines could be created, but not the other. In fact, I needed a distribution of points with two axes of curvature, so that literally there were no possibilities for creating lines in space with any periodicity.

Offset concentric intersection packing

Well, well, two axes of curvature, no problem. I will simply take two circles and place points on my pattern, in which the concentric rings of these circles intersect:


It looked beautiful. I felt that I could already be close to a solution. Looking at the distribution from different angles, I saw that the main problem was that the curvature still remained visible, because it was a bit weak in order to visually hide the space between the points. I thought that it was possible to increase the curvature, but then I thought - what if, let's say, I will shift every third concentric ring of a circle? Instead of evenly distributed concentric rings, the radius of each third ring will be slightly shifted to introduce noise, and also slightly reduce the noticeable repeatability of the pattern. I remind you that this is a fully deterministic displacement, that is, in fact there is no chance:


Bingo. That is the kind of coverage I need! Dense visible coverage and absolute inability to notice spaces except where you stand (which, of course, cannot be corrected by any pattern except an increase in the number of points and literally a complete coverage of space). It was possible to completely eliminate the problem areas of the review that appeared in the algorithm without offsets:


There is also a bonus - you can use much fewer points than I took for blue noise with spaces, to get a visually better coverage:

Why so many failures?

As in the case of most difficult problems, when you dive into it, you often cannot find the right view of things. That is why this is called "dive." Anyway, looking back at the previous few days, I see the fundamental mistake of my approach.

I started with a pretty good random coverage - with blue noise, and I wanted to improve it. But if you remember what is an accident and how it works, then you can realize a fairly obvious truth: an accident is never optimal. For any set of criteria, the probability that a set of optimal input data can be chosen randomly is extremely small. If you take 100 dice and throw them, then you will not get 600. Perhaps never (you can of course use the D20 bones, but I want this metaphor to be understandable and not playing D & D). It is also impossible to limit randomness in any way. Even if you take all the cubes and replace all units, twos, threes and fours for sixes, that is, only fives and sixes remain on the cube, you still almost never throw away 600. Even if you do this and transfer all the fives, you will have to do it's seven times until you get all the sixes.

Therefore, if you want to do something optimal, then there is a chance that you will have to go beyond random algorithms. I continued to look for schemes that could create optimality from randomness, but this was very unlikely. Since the blue noise is quite a good pattern for my purposes, I tried to find a fracture in randomness, and each scheme was doomed to failure, because there is simply no better random scheme. To make this jump, I had to go from chaos to order and directly control the optimum.

In fact, this is a very important lesson that can be learned from this experience. The pattern itself is not so important. It is important to understand whether your task is related to optimization, and if so, is it necessary for some other reason to use chance? If yes, then you have to choose something less than optimal. If you do not do this, then in order to move on, you will have to abandon chance.

As it happens with many discoveries, if you think about it, it is quite simple and practically explains itself. , , .

,

, ? , , , , « ». , , . And that's fine. , .

, . , , , The Witness - . , , , .

. , « » . , « » , « », . , , . , , .