Naive Spellchecking, or search for the nearest words from the dictionary by Levenshtein's metric on Scala

Greetings This article will show the algorithm for finding the closest to a given word from the corpus in terms of the Levenshten metric. The naive spellchecking is named because it does not take into account neither the morphology, nor the context, nor the probability of the appearance of the corrected word in the sentence, however, as a first approximation, it will completely do. Also, the algorithm can be extended to search for the nearest sequences from any other comparable objects, rather than a simple alphabet from Chars, and, after doping, it can be adapted to take into account the probabilities of the appearance of corrected words. But in this article we will focus on the basic algorithm for words of a certain alphabet, say, English.

The code in the article will be on Scala.

All interested in asking under the cat.

Intro

Generally speaking, specialized data structures exist for searching in a metric space, such as VP-Tree (Vantage Point Tree). However, experiments show that for a word space with Levenshtein metric, the VP-tree works extremely poorly. The reason is simple - this metric space is very dense. A word of, say, 4 letters, has a huge number of neighbors at a distance of 1. At greater distances, the number of options becomes comparable to the size of the whole set, which makes the search in a VP-tree no more productive than a linear search over a set. Fortunately, there is a more optimal solution for strings, and now we will analyze it.
')

Description

For compact storage of a set of words with a common prefix, we use a data structure such as boron (trie).


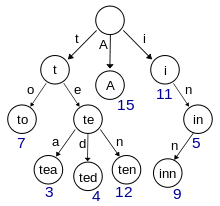
In a nutshell, the algorithm is described as a simple search by Dijkstra's algorithm on an implicit graph of options for the prefix match of the search word and the word in bor (trie). In the fuzzy search, the graph nodes are the above options, and the edge weights are the actual Levenshtein distance of a given string prefix and a boron node.

Basic implementation of boron

To begin with, we will describe a boron node, we will write an algorithm for inserting and a clear search for a word in boron. Fuzzy search leave for a snack.

class Trie( val ends: Boolean = false, // whether this node is end of some string private val parent: Trie = null, private val childs : TreeMap[Char, Trie] = null, val value : Char = 0x0) 

As you can see, nothing supernatural. A boron node is an object with a link to the parent, a Map of the links to the descendants, the literal value of the node, and a flag indicating whether the node is the end node for any string.

Now we describe a clear search in boron:

 /// exact search def contains(s: String) = { @tailrec def impl(t: Trie, pos: Int): Boolean = if (s.size < pos) false else if (s.size == pos) t.ends else if (t.childs == null) false else if (t.childs.contains(s(pos)) == false) false else impl(t.childs(s(pos)), pos + 1) impl(this, 0) } 

Nothing complicated. We descend through the children of the node until we meet a coincidence (t.ends) or see that there is no place to descend further.

Now - insert:

 /// insertion def +(s: String) = { def insert(trie: Trie, pos: Int = 0) : Trie = if (s.size < pos) trie else if (pos == 0 && trie.contains(s)) trie else if (s.size == pos) if (trie.ends) trie else new Trie(true, trie.parent, trie.childs, trie.value) else { val c = s(pos) val children = Option(trie.childs).getOrElse(TreeMap.empty[Char, Trie]) val child = children.getOrElse( c, new Trie(s.size == pos + 1, trie, null, c)) new Trie( trie.ends, trie.parent, children + (c, insert(child, pos + 1)), trie.value) } insert(this, 0) } 

Our boron is immutable, so the function + returns us a new boron.

Building a boron from a body of words looks something like this:

 object Trie { def apply(seq: Iterator[String]) : Trie = seq.filter(_.nonEmpty).foldLeft(new Trie)(_ + _) def apply(seq: Seq[String]) : Trie = apply(seq.iterator) } 

Basic construction is ready.

Fuzzy search, basic function

We describe the graph node:

 case class Variant(val pos: Int, val node: Trie)(val penalty: Int) 

Pos is the position at which the prefix of the search string ends in the considered variant. Node - boron prefix in the current version. Penalty - Levenshtein distance of the string prefix and the boron prefix.

The curried case-class means that the compiler will generate the equals / hashCode function only for the first argument list. Penalty versus Variant are not counted .

Looking through the nodes of a graph with non-decreasing penalty is managed by a function with this signature:

 def prefixes(toFind: String): Stream[Variant] 

To implement it, we write a small helper that generates a Stream with a generator function:

  def streamGen[Ctx, A] (init: Ctx)(gen: Ctx => Option[(A, Ctx)]): Stream[A] = { val op = gen(init) if (op.isEmpty) Stream.Empty else op.get._1 #:: streamGen(op.get._2)(gen) } 

Now we implement the immutable context of the search, which we will pass to the function above, and which contains everything that is needed to iterate over the nodes of an implicit graph using the Dijkstra algorithm: a priority queue and many visited nodes:

  private class Context( // immutable priority queue, Map of (penalty-, prefix pos+) -> List[Variant] val q: TreeMap[(Int, Int), List[Variant]], // immutable visited nodes cache val cache: HashSet[Variant]) { // extract from 'q' value with lowest penalty and greatest prefix position def pop: (Option[Variant], Context) = { if (q.isEmpty) (None, this) else { val (key, list) = q.head if (list.tail.nonEmpty) (Some(list.head), new Context(q - key + (key, list.tail), cache)) else (Some(list.head), new Context(q - key, cache)) } } // enqueue nodes def ++(vars: Seq[Variant]) = { val newq = vars.filterNot(cache.contains).foldLeft(q) { (q, v) => val key = (v.penalty, v.pos) if (q.contains(key)) { val l = q(key); q - key + (key, v :: l) } else q + (key, v :: Nil) } new Context(newq, cache) } // searches node in cache def apply(v: Variant) = cache(v) // adds node to cache; it marks it as visited def addCache(v: Variant) = new Context(q, cache + v) } private object Context { def apply(init: Variant) = { // ordering of prefix queue: min by penalty, max by prefix pos val ordering = new Ordering[(Int, Int)] { def compare(v1: (Int, Int), v2: (Int, Int)) = if (v1._1 == v2._1) v2._2 - v1._2 else v1._1 - v2._1 } new Context( TreeMap(((init.penalty, init.pos), init :: Nil))(ordering), HashSet.empty[Variant]) } } 

The node queue is made from simple immutable treemaps. Nodes in the queue are sorted in ascending penalty and descending prefix pos.

Well, finally the generator itself stream options:

  // impresize search lookup, returns stream of prefix match variants with lowest penalty def prefixes(toFind: String) : Stream[Variant] = { val init = Variant(0, this)(0) // returns first unvisited node @tailrec def whileCached(ctx: Context): (Option[Variant], Context) = { val (v, ctx2) = ctx.pop if (v.isEmpty) (v, ctx2) else if (!ctx2(v.get)) (Some(v.get), ctx2) else whileCached(ctx2) } // generates graph edges from current node def genvars(v: Variant): List[Variant] = { val replacePass: List[Variant] = if (v.node.childs == null) Nil else v.node.childs.toList flatMap { pair => val (key, child) = pair val pass = Variant(v.pos, child)(v.penalty + 1) :: Nil if (v.pos < toFind.length) Variant(v.pos + 1, child)(v.penalty + {if (toFind(v.pos) == key) 0 else 1}) :: pass else pass } if (v.pos != toFind.length) { Variant(v.pos + 1, v.node)(v.penalty + 1) :: replacePass } else replacePass } streamGen(Context(init)) { ctx => val (best, ctx2) = whileCached(ctx) best.map { v => (v, (ctx2 ++ genvars(v)).addCache(v)) } } } 

Of course, genvars deserves the most attention. For a given node of the graph, it generates edges emanating from it. For each descendant of the boron node of this search option, we generate a variant with an insert character

 val pass = Variant(v.pos, child)(v.penalty + 1) 

and replacing the character

 Variant(v.pos + 1, child)(v.penalty + {if (toFind(v.pos) == key) 0 else 1}) 

If you have not reached the end of the line, then the generma also has the option of removing the character

 Variant(v.pos + 1, v.node)(v.penalty + 1) 

Fuzzy search, usability

Of course, the prefixes function is not suitable for general use. Let's write wrappers that allow us to search more or less meaningfully. To begin with, we will limit the search of variants to some reasonable value of penalty to prevent the algorithm from sticking on any word for which there is no more or less adequate replacement in the dictionary.

 def limitedPrefixes(toFind: String, penaltyLimit: Int = 5): Stream[Variant] = { prefixes(toFind).takeWhile(_.penalty < penaltyLimit) } 

Next, we filter the options with a full, rather than a prefix match, that is, those that have pos equal to the length of the search string, and node points to the end node with the ends == true flag:

 def matches(toFind: String, penaltyLimit: Int = 5): Stream[Variant] = { limitedPrefixes(toFind, penaltyLimit).filter { v => v.node.ends && v.pos == toFind.size } } 

Finally, we will convert the stream of variants into the stream of words. To do this, in the Trie class, we will write a code that returns the found word:

 def makeString() : String = { @tailrec def helper(t: Trie, sb: StringBuilder): String = if (t == null || t.parent == null) sb.result.reverse else { helper(t.parent, sb += t.value) } helper(this, new StringBuilder) } 

Nothing complicated. Climb up on parenting, recording the values ​​of the nodes, until we meet the boron root.

And finally:

 def matchValues(toFind: String, penaltyLimit: Int = 5): Stream[String] = { matches(toFind, penaltyLimit).map(_.node.makeString) } 

Total

I must say that the function matches is very versatile. Using it, you can search for K nearest, making

 matches(toFind).take(k).map(_.node.makeString) 

or search for Delta-closest, that is, lines at a distance not more than D:

 matches(toFind).takeWhile(_.penalty < d).map(_.node.makeString) 

Another algorithm can be expanded by introducing different weights for inserting / deleting / replacing characters. You can add specific replace / delete / insert counters to the Variant class. Trie can be generalized, so that it is possible to store values ​​in the end nodes, and not only strings, but also indexed sequences of any comparable types of keys can be used as keys. You can also mark each boron node with a probability to meet it (for the end node it is the probability to meet the word + the probability to meet all the descendant words, for the intermediate one - only the sum of the probabilities of the descendants) and to take this weight into account when calculating the penalty, but this is already beyond the scope of this article .

I hope it was interesting. Code here