Recover Huffman Tables in Intel ME 11.x
Today, Positive Technologies expert Dmitry Sklyarov at the Black Hat conference in London will talk about the structure of the file system on which Intel CSME / ME version 11.x is located and some files for this system. We present to your attention his article on the recovery of Huffman tables in Intel ME 11.x.
As you know , many Intel ME 11.x modules are stored in a flash memory in a packaged form, and two algorithms are used for compression - LZMA and Huffman Encoding . For LZMA, there is a public implementation that can be used to decompress, but for Huffman everything is more complicated. The Huffman Encoding unpacker in ME is implemented at the hardware level, and the construction of equivalent program code is a complex and non-standard task.
')
After reading the source texts that are part of the unhuffme project, it is easy to see that for previous versions of ME there are two sets of Huffman tables and there are two tables in each of the sets. The presence of two tables (one for code and one for data) is probably due to the fact that the statistical properties of code and data are very different.
Also noteworthy are the following properties:
It can be assumed that in the Huffman tables for ME 11.x, the last three properties are also observed. Then, to fully restore the tables, you need to find the following:
To obtain information about the individual modules, you can use the existing knowledge about the internal structures of the firmware .
Having examined the Lookup Table, which is part of the Code Directory Directory Partition, it is easy to determine for which modules Huffman coding is applied, where their packed data starts, and what size the module will have after unpacking.
Having examined the Module Attributes Extension for a specific module, it is easy to find the size of the compressed and decompressed data and SHA256 from the unpacked data.
Having fluently analyzed several firmware for ME 11.x, it is easy to notice that the data size after unpacking by Huffman is always a multiple of the page size (4096 == 0x1000 bytes). At the beginning of the packed data is an array of four-byte integer values. The number of array elements corresponds to the number of pages in the unpacked data.
For example, for a module of size 81920 == 0x14000 bytes, the array will occupy 80 == 0x50 bytes and consist of 20 == 0x14 elements.

The two high-order bits of each of the Little-Endian values store the table number (0b01 for the code and 0b11 for the data). In the remaining 30 bits, the offset of the beginning of the compressed page relative to the end of the array of offsets is stored. The above snippet describes 20 pages:

It is noteworthy that the packaged data offsets for each page are sorted in ascending order, and the packed data size for each page does not appear explicitly anywhere. In the example above, the packed data for each specific page begins at the boundary of a multiple of 64 = 0x40 bytes, and the unused areas are filled with zeros. But for other modules, you can establish that the presence of alignment is not mandatory. This suggests that the unpacker stops when the amount of data in the unpacked page reaches 4096 bytes.
Since we know the total size of the packaged module (from the Module Attributes Extension), we can divide the packaged data into separate pages and work with each page separately. The beginning of a packed page is determined from the array of offsets, and the size by the offset of the beginning of the next page or the total size of the module. In this case, after the packed data, there can be an arbitrary number of insignificant bits (these bits can have any values, but in practice they are usually zero).

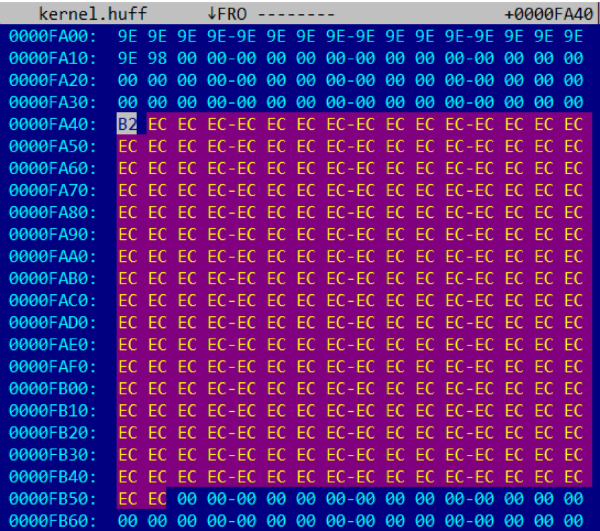
The screenshot shows that the last compressed page (starting at offset 0xFA40) consists of byte 0xB2 == 0b10110010, followed by 273 bytes with the value 0xEC == 0b11101100, and then only zeros. Since the bit sequence 11101100 (or 01110110) is repeated 273 times, we can assume that it encodes 4096/273 == 15 identical bytes (most likely with values of 0x00 or 0xFF). Then the bit sequence 10110010 (or 1011001) encodes 4096-273 * 15 == 1 byte.
This agrees well with the assumption that each code sequence encodes an integer number of bytes (from 1 to 15 inclusive). However, it is not possible to fully restore the Huffman tables in this way.
As was shown earlier , in different versions of firmware for ME 11, modules with the same name can be packaged with different algorithms. If you parse the Module Attributes Extension for modules of the same name, packaged with both LZMA and Huffman, and extract the SHA256 values for each module, you will not find a single pair of modules packaged with different algorithms and having the same hash values.
But if we recall that for modules packed with LZMA, SHA256 is usually considered to be compressed data, and to calculate SHA256 for modules after unpacking LZMA, a lot of suitable pairs will be found. And for each such “paired” module, we immediately get several pairs of pages - in a packaged Huffman and unpacked form.
The presence of a large set of pages in compressed and open form (separately for code and data) allows you to recover all the code sequences used in these pages. The solution of the problem is located at the junction of linear algebra and search engine optimization methods. Probably, you can build a rigorous mathematical model that takes into account all the limitations, but since the task is one-time, it turned out to be faster to do part of the work manually, and to automate part.
The most important thing is to at least approximately determine the Shape (points of change in the length of code sequences). For example, that 7-bit sequences have values from 1111111 to 1110111, 8-bit from 11101101 to 10100011, etc. Since Canonical Huffman Coding is used, knowledge of Shape allows you to determine the length of the following code sequence (the shortest sequence consists of only one , the longest - only from zeros, and the smaller the value, the longer the sequence).
Since we do not know the exact size of the compressed data, all sequences consisting of only zero bits can be thrown out of the “tail” (since they are the longest, and the appearance of the rarest code sequence in the last position is unlikely).
When each compressed page can be represented as a set of code sequences, you can begin to determine the lengths of the values they encode. The sum of the lengths of the encoded values for each page should be 4096 bytes. This allows you to create a system of linear equations, where the lengths of the encoded values are unknown, the coefficients are the number of occurrences of the corresponding code sequence in the compressed page, and the place of the free term is always 4096. The code and data pages can be processed together, since for identical code sequences the lengths of the coded values must match.
With enough pages (and equations), the only solution to the system is easily found by the Gauss method. And having the plaintext, knowing the length of each value and the order in which they are followed, it is easy to get a match for the code sequences and the values they encode.
After processing all the available “paired” pages, it will turn out to find out the values for approximately 70% of the sequences from the code table and 68% of the sequences from the data table. Lengths will be known for about 92% of the sequences. And there will remain some uncertainty in the Shape: in some places either one value of a shorter length or two values of a greater length can be used, and it is impossible to determine the boundary until one of the values is found in the packed data.
Now we can proceed to the restoration of values for code sequences that are found only in modules for which there are no open texts.
If a sequence with an unknown length is encountered, another line is added to the system of equations, and this allows you to quickly determine the length. But how to determine the value without having a clear text?
Fortunately, SHA256 from the unpacked module is stored in the metadata. And if we correctly guess the value of all unknown code sequences in all pages that make up the module, the calculated SHA256 value should match the SHA256 value from the Module Attributes Extension.
When the total length of unknown sequences is 1 or 2 bytes, the unknown bytes are simply found by a frontal search. You can do the same with 3 and even 4 unknown bytes (especially if they are located close to the end of the module), but the search can take from several hours to several days on one core (it is easy to parallelize to several cores or machines). Attempts to search 5 or more bytes were not made.
Thus it is possible to recover several more code sequences (and several modules). But then there are only modules in which the total amount of unknown bytes exceeds the capabilities of the brute-force selection.
However, the presence of a large number of modules, slightly differing from each other, allows you to apply different heuristics and use them to find the values of unknown code sequences.
Since there are two Huffman tables in the unpacker, the compressor tries to compress the data of each of them, and leaves the version that takes up less space. As a result, the division into "code" and "data" is conditional. And when changing part of a page, another table may be more efficient. That is, looking at other versions of the same module, you can find identical fragments that were packed by another table, and so recover unknown bytes.
When one code sequence occurs many times in one (or different) modules (for example, in code and in data), it is often easy to determine which restrictions are imposed on unknown values.
In the field of these modules, constants and offsets are quite common (for example, to text strings or functions). Constants can be common for different modules (for example, for hashing functions and encryption algorithms), and offsets are unique for each version of the module, but should refer to the same (or very similar) pieces of data or code. And their values are very easy to restore.
Some pieces of ME code were obviously borrowed from open-source projects (for example, wpa_supplicant), and fragments of text strings are easily guessed by context and by peeping at the source code.
Looking at the sources and finding the text of the function, for the compiled code of which is unknown a few bytes, you can work with the compiler and guess which values are appropriate in this place.
Since in different (but close) versions of one module there should not be strong differences, sometimes it is enough to find an equivalent function in a module of another version, and by its code understand what should be in unknown bytes.
If the code is not taken from public sources, some fragment is unknown in all available versions of the module, and is not found in any other module (that’s how it was with the amt module) you can find the same place (for example, in ME 10), find out the logic functions, and then project it to an unknown place in ME 11.x.
Starting from the modules in which there were the least unknown sequences, and combining different heuristics, it was possible to increment the known part of the Huffman tables step by step (each time checking the correctness of the assumptions by calculating SHA256). With increasing coverage, the modules, where the number of unknown sequences was initially measured in dozens, turned out to be not so frightening. The process looked convergent, but everything came up against amt.
This module is the largest in size (on the order of 2 megabytes, approximately 30% of the total volume), contains many code sequences that are not found in any other module, but are found in all versions of amt. You can guess several sequences with a high probability, but the only way to test an assumption is to guess them all (so that SHA256 matches). Thanks to the invaluable help of Maxim Goryachiy, we managed to overcome this barrier, as a result of which we were able to unpack any of the modules contained in the firmware we have and packed with the Huffman algorithm.
Over time, new firmware appeared, and not previously encountered code words appeared in them. But each time one of the heuristics worked, the module was successfully unpacked and the coverage of the tables increased.
By mid-June 2017, we were able to recover approximately 89.4% of the sequences for the code table and 86.4% of the sequences for the data table. But the chances of building a reasonable time 100% coverage of the tables through the analysis of new modules are very weak.
On June 19, fragments of Huffman tables were published on GitHub by a user with the nickname IllegalArgument, covering 80.8% of the sequences for the code table and 78.1% of the sequences for the data table. Probably, the author (or authors) used a similar approach based on the analysis of available firmware. And in the published tables there was nothing new.
And on July 17, Mark Yermolov and Maxim Goryachiy got the opportunity to find out the unpacked values for any compressed data. We prepared 4 compressed pages (two for the code and for the data), and restored all 1519 sequences for both tables .
At the same time, one strange place was found. In the Huffman table for data, the value 00410E088502420D05 corresponds to both the sequence 10100111 (8 bits long) and the sequence 000100101001 (12 bits long). This is a clear redundancy, but most likely it is due to a random error.
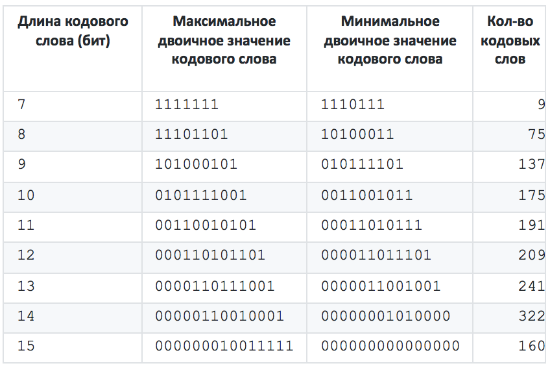
The resulting Shape is as follows:
Posted by Dmitry Sklyarov, Positive Technologies

As you know , many Intel ME 11.x modules are stored in a flash memory in a packaged form, and two algorithms are used for compression - LZMA and Huffman Encoding . For LZMA, there is a public implementation that can be used to decompress, but for Huffman everything is more complicated. The Huffman Encoding unpacker in ME is implemented at the hardware level, and the construction of equivalent program code is a complex and non-standard task.
')
Previous versions of ME
After reading the source texts that are part of the unhuffme project, it is easy to see that for previous versions of ME there are two sets of Huffman tables and there are two tables in each of the sets. The presence of two tables (one for code and one for data) is probably due to the fact that the statistical properties of code and data are very different.
Also noteworthy are the following properties:
- For different sets of tables, the lengths of codewords differ (7–19 and 7–15 bits, inclusive).
- Each code sequence encodes an integer number of bytes (from 1 to 15 inclusive).
- Both sets use Canonical Huffman Coding (this allows you to quickly determine the length of the next code word when unpacking).
- Within one set of lengths, the encoded values for any codeword are the same in all tables (Code and Data).
Formulation of the problem
It can be assumed that in the Huffman tables for ME 11.x, the last three properties are also observed. Then, to fully restore the tables, you need to find the following:
- range of codeword lengths;
- boundaries of codeword values having the same length (Shape);
- the length of the encoded sequences for each code word;
- coded values for each codeword in both tables.
Splitting compressed data into separate pages
To obtain information about the individual modules, you can use the existing knowledge about the internal structures of the firmware .
Having examined the Lookup Table, which is part of the Code Directory Directory Partition, it is easy to determine for which modules Huffman coding is applied, where their packed data starts, and what size the module will have after unpacking.
Having examined the Module Attributes Extension for a specific module, it is easy to find the size of the compressed and decompressed data and SHA256 from the unpacked data.
Having fluently analyzed several firmware for ME 11.x, it is easy to notice that the data size after unpacking by Huffman is always a multiple of the page size (4096 == 0x1000 bytes). At the beginning of the packed data is an array of four-byte integer values. The number of array elements corresponds to the number of pages in the unpacked data.
For example, for a module of size 81920 == 0x14000 bytes, the array will occupy 80 == 0x50 bytes and consist of 20 == 0x14 elements.

The two high-order bits of each of the Little-Endian values store the table number (0b01 for the code and 0b11 for the data). In the remaining 30 bits, the offset of the beginning of the compressed page relative to the end of the array of offsets is stored. The above snippet describes 20 pages:

It is noteworthy that the packaged data offsets for each page are sorted in ascending order, and the packed data size for each page does not appear explicitly anywhere. In the example above, the packed data for each specific page begins at the boundary of a multiple of 64 = 0x40 bytes, and the unused areas are filled with zeros. But for other modules, you can establish that the presence of alignment is not mandatory. This suggests that the unpacker stops when the amount of data in the unpacked page reaches 4096 bytes.
Since we know the total size of the packaged module (from the Module Attributes Extension), we can divide the packaged data into separate pages and work with each page separately. The beginning of a packed page is determined from the array of offsets, and the size by the offset of the beginning of the next page or the total size of the module. In this case, after the packed data, there can be an arbitrary number of insignificant bits (these bits can have any values, but in practice they are usually zero).

The screenshot shows that the last compressed page (starting at offset 0xFA40) consists of byte 0xB2 == 0b10110010, followed by 273 bytes with the value 0xEC == 0b11101100, and then only zeros. Since the bit sequence 11101100 (or 01110110) is repeated 273 times, we can assume that it encodes 4096/273 == 15 identical bytes (most likely with values of 0x00 or 0xFF). Then the bit sequence 10110010 (or 1011001) encodes 4096-273 * 15 == 1 byte.
This agrees well with the assumption that each code sequence encodes an integer number of bytes (from 1 to 15 inclusive). However, it is not possible to fully restore the Huffman tables in this way.
Finding pairs of "compressed text - clear text"
As was shown earlier , in different versions of firmware for ME 11, modules with the same name can be packaged with different algorithms. If you parse the Module Attributes Extension for modules of the same name, packaged with both LZMA and Huffman, and extract the SHA256 values for each module, you will not find a single pair of modules packaged with different algorithms and having the same hash values.
But if we recall that for modules packed with LZMA, SHA256 is usually considered to be compressed data, and to calculate SHA256 for modules after unpacking LZMA, a lot of suitable pairs will be found. And for each such “paired” module, we immediately get several pairs of pages - in a packaged Huffman and unpacked form.
Shape, Length, Value
The presence of a large set of pages in compressed and open form (separately for code and data) allows you to recover all the code sequences used in these pages. The solution of the problem is located at the junction of linear algebra and search engine optimization methods. Probably, you can build a rigorous mathematical model that takes into account all the limitations, but since the task is one-time, it turned out to be faster to do part of the work manually, and to automate part.
The most important thing is to at least approximately determine the Shape (points of change in the length of code sequences). For example, that 7-bit sequences have values from 1111111 to 1110111, 8-bit from 11101101 to 10100011, etc. Since Canonical Huffman Coding is used, knowledge of Shape allows you to determine the length of the following code sequence (the shortest sequence consists of only one , the longest - only from zeros, and the smaller the value, the longer the sequence).
Since we do not know the exact size of the compressed data, all sequences consisting of only zero bits can be thrown out of the “tail” (since they are the longest, and the appearance of the rarest code sequence in the last position is unlikely).
When each compressed page can be represented as a set of code sequences, you can begin to determine the lengths of the values they encode. The sum of the lengths of the encoded values for each page should be 4096 bytes. This allows you to create a system of linear equations, where the lengths of the encoded values are unknown, the coefficients are the number of occurrences of the corresponding code sequence in the compressed page, and the place of the free term is always 4096. The code and data pages can be processed together, since for identical code sequences the lengths of the coded values must match.
With enough pages (and equations), the only solution to the system is easily found by the Gauss method. And having the plaintext, knowing the length of each value and the order in which they are followed, it is easy to get a match for the code sequences and the values they encode.
Unknown sequences
After processing all the available “paired” pages, it will turn out to find out the values for approximately 70% of the sequences from the code table and 68% of the sequences from the data table. Lengths will be known for about 92% of the sequences. And there will remain some uncertainty in the Shape: in some places either one value of a shorter length or two values of a greater length can be used, and it is impossible to determine the boundary until one of the values is found in the packed data.
Now we can proceed to the restoration of values for code sequences that are found only in modules for which there are no open texts.
If a sequence with an unknown length is encountered, another line is added to the system of equations, and this allows you to quickly determine the length. But how to determine the value without having a clear text?
Verifier and brute-force
Fortunately, SHA256 from the unpacked module is stored in the metadata. And if we correctly guess the value of all unknown code sequences in all pages that make up the module, the calculated SHA256 value should match the SHA256 value from the Module Attributes Extension.
When the total length of unknown sequences is 1 or 2 bytes, the unknown bytes are simply found by a frontal search. You can do the same with 3 and even 4 unknown bytes (especially if they are located close to the end of the module), but the search can take from several hours to several days on one core (it is easy to parallelize to several cores or machines). Attempts to search 5 or more bytes were not made.
Thus it is possible to recover several more code sequences (and several modules). But then there are only modules in which the total amount of unknown bytes exceeds the capabilities of the brute-force selection.
Heuristics
However, the presence of a large number of modules, slightly differing from each other, allows you to apply different heuristics and use them to find the values of unknown code sequences.
Using the second Huffman table
Since there are two Huffman tables in the unpacker, the compressor tries to compress the data of each of them, and leaves the version that takes up less space. As a result, the division into "code" and "data" is conditional. And when changing part of a page, another table may be more efficient. That is, looking at other versions of the same module, you can find identical fragments that were packed by another table, and so recover unknown bytes.
Reuse
When one code sequence occurs many times in one (or different) modules (for example, in code and in data), it is often easy to determine which restrictions are imposed on unknown values.
Constants and tables with offsets
In the field of these modules, constants and offsets are quite common (for example, to text strings or functions). Constants can be common for different modules (for example, for hashing functions and encryption algorithms), and offsets are unique for each version of the module, but should refer to the same (or very similar) pieces of data or code. And their values are very easy to restore.
String constants from open libraries
Some pieces of ME code were obviously borrowed from open-source projects (for example, wpa_supplicant), and fragments of text strings are easily guessed by context and by peeping at the source code.
Open Library Code
Looking at the sources and finding the text of the function, for the compiled code of which is unknown a few bytes, you can work with the compiler and guess which values are appropriate in this place.
Similar functions in modules of another version
Since in different (but close) versions of one module there should not be strong differences, sometimes it is enough to find an equivalent function in a module of another version, and by its code understand what should be in unknown bytes.
Similar features in previous versions of ME
If the code is not taken from public sources, some fragment is unknown in all available versions of the module, and is not found in any other module (that’s how it was with the amt module) you can find the same place (for example, in ME 10), find out the logic functions, and then project it to an unknown place in ME 11.x.
Process convergence
Starting from the modules in which there were the least unknown sequences, and combining different heuristics, it was possible to increment the known part of the Huffman tables step by step (each time checking the correctness of the assumptions by calculating SHA256). With increasing coverage, the modules, where the number of unknown sequences was initially measured in dozens, turned out to be not so frightening. The process looked convergent, but everything came up against amt.
This module is the largest in size (on the order of 2 megabytes, approximately 30% of the total volume), contains many code sequences that are not found in any other module, but are found in all versions of amt. You can guess several sequences with a high probability, but the only way to test an assumption is to guess them all (so that SHA256 matches). Thanks to the invaluable help of Maxim Goryachiy, we managed to overcome this barrier, as a result of which we were able to unpack any of the modules contained in the firmware we have and packed with the Huffman algorithm.
Over time, new firmware appeared, and not previously encountered code words appeared in them. But each time one of the heuristics worked, the module was successfully unpacked and the coverage of the tables increased.
Final touch
By mid-June 2017, we were able to recover approximately 89.4% of the sequences for the code table and 86.4% of the sequences for the data table. But the chances of building a reasonable time 100% coverage of the tables through the analysis of new modules are very weak.
On June 19, fragments of Huffman tables were published on GitHub by a user with the nickname IllegalArgument, covering 80.8% of the sequences for the code table and 78.1% of the sequences for the data table. Probably, the author (or authors) used a similar approach based on the analysis of available firmware. And in the published tables there was nothing new.
And on July 17, Mark Yermolov and Maxim Goryachiy got the opportunity to find out the unpacked values for any compressed data. We prepared 4 compressed pages (two for the code and for the data), and restored all 1519 sequences for both tables .
At the same time, one strange place was found. In the Huffman table for data, the value 00410E088502420D05 corresponds to both the sequence 10100111 (8 bits long) and the sequence 000100101001 (12 bits long). This is a clear redundancy, but most likely it is due to a random error.
The resulting Shape is as follows:

Posted by Dmitry Sklyarov, Positive Technologies
Source: https://habr.com/ru/post/344056/
All Articles