Explanation of SNARKs. From calculations to polynomials, the Pinocchio protocol and the pairing of elliptic curves (translation)
Hi, Habr! I present to your attention the translation of ZCash blog articles, which describe the mechanism of the evidence system with zero disclosure of SNARKs used in the ZCash cryptocurrency (and not only).
Source: https://z.cash/blog/snark-explain5.html
Previous articles:
')
Part 1: Explaining SNARKs. Homomorphic hiding and blind computation of polynomials (translation)
Part 2: Explaining SNARKs. Knowledge of the adopted coefficient and reliable blind calculation of polynomials (translation)
Starting the final part of the translation, I want to say that we live in a truly amazing time. The time when higher mathematics has the ability to almost immediately be involved in software development and we can observe “in action” the results of the work of mathematicians of technological institutes in advanced things based on blockchains and data exchanges.
Well, I will not detain further your attention, let's move on to the most interesting ...
In previous articles we have developed a specific mechanism for working with polynomials. In this part, we will learn how to transform the statements we want to prove and verify in the language of polynomials. The idea of using polynomials in this way begins with the pioneering work of 1991 by Lund, Fortwon, Karloff and Nisan (Carsten Lund, Lance Fortnow, Howard Karloff - University of Chicago AND Noam Nisan - Hebrew University).
In 2013, another yet another breakthrough work by Gennaro, Gentry, Parno and Raikova (Rosario Gennaro, Craig Gentry, Bryan Parno, Mariana Raykova) comes out. This work identified extremely convenient transformations of computations into polynomials called the Quadratic Arithmetic Program (QAP). KAP became the basis for modern zk-SNARK constructions, in particular, those used in ZCash cryptocurrency.
In the first part of the article, the transformations of the calculations in the CAP will be explained by example. Even if you focus on a small example, and not on a general definition, you have to spend enough time to understand it to begin with. So be prepared for a certain mental effort :)
Suppose Alice wants to prove to Bob that he knows such that . The first step is to present the calculation with in the form of an arithmetic circuit.
An arithmetic circuit consists of calculated arithmetic operations, called transitions, such as addition and multiplication, with connections between them. In our case, the scheme looks like this:
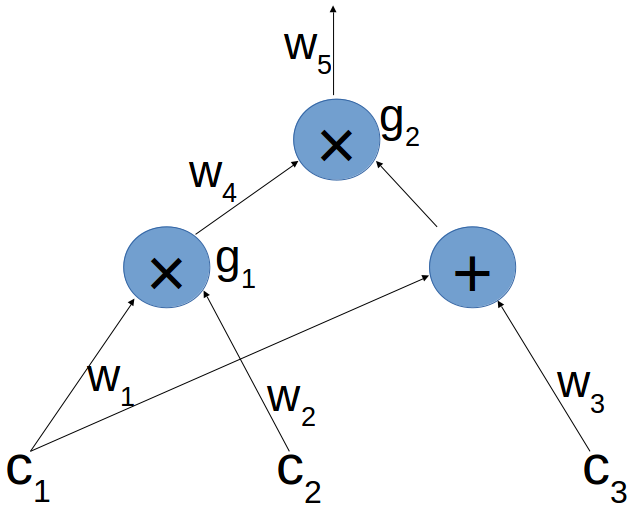
The bottom connectors are input parameters, and the top output connection is the result of calculating the entire circuit for these input parameters.
As can be seen in the figure, connectors and transitions of the circuit are designated in a certain way. These rules will be necessary for the next step, namely the transfer of the scheme in the CAP:
A valid assignment set for the scheme is the assignment of values for labeled transitions, where the output value of each multiplication transition is the result of the product of the corresponding inputs.
So, for our scheme, the valid assignment set is: Where and
Following this terminology, Alice wants to prove that she knows a valid assignment set such that . The next step is to translate this statement into a polynomial using CAP.
Each transition multiplication must be correlated with the field element: will be correlated with and with . We call the points {1, 2} our target points . Now we need to define a set of "left connecting polynomials" , "Right connective polynomials" and "output connecting polynomials" .
The main idea of this action is to ensure that the values of the polynomials are zero at all target points, except the target point of the multiplication transition, in which they are involved.
Speaking specifically, since left, right and output connectors respectively can define since the polynomial equals one at point 1 corresponding and is zero at point 2 corresponding .
notice, that and both are right inputs . Therefore, similarly, we define , because equals one at target point 2 corresponding and zero at another target point.
Denote all other polynomials as zero polynomials.
With fixed values they are used as coefficients for determining the left, right, and output "total" polynomials. That is, you can determine:
$ inline $ L: = Σ ^ 5_ {i = 1} c_i⋅L_i, R: = Σ ^ 5_ {i = 1} c_i⋅R_i, O: = Σ ^ 5_ {i = 1} c_i⋅O_i $ inline $
Then we define the polynomial
Now, after all these definitions, we can form a central definition: is a valid scheme assignment set if and only if P takes a zero value at all target points.
Let's see this using our example. Suppose that were defined as stated above with some . Let's calculate all these polynomials at target point 1 :
Of all only is non-zero at point 1 . So, . Similarly, we get and .
Consequently, . Similar can be obtained .
In other words, P vanishes at target points if and only if is a valid assignment set.
Now we will use the following algebraic fact: for the polynomial P and the point we have if and only if the polynomial divides P without remainder, i.e. for some polynomial H.
Having determined the target polynomial in this way: , we obtain that T divides P if and only if is a valid assignment set.
Based on the foregoing, we define the CAP as follows:
The quadratic arithmetic program Q of order d and size m consists of polynomials and the target polynomial T of order d .
Assignment Set satisfies Q if, defining $ inline $ L: = Σ ^ m_ {i = 1} c_i ⋅ L_i, R: = Σ ^ m_ {i = 1} c_i⋅ R_i, O: = Σ ^ m_ {i = 1} c_i⋅ O_i $ inline $ and , there exists T , which divides without remainder P.
Following this terminology, Alice wants to prove that she knows the set of assignments satisfying the CAP defined above, where ,
Let's summarize this part. We saw a statement like "I know such that »Can be translated into an equivalent statement about polynomials using CAP. Next, we will look at an efficient protocol for confirming knowledge of a valid set of CAP assignments.
Earlier, we showed that the statement that Alice wants to prove to Bob can be transformed into an equivalent form in the "language of polynomials," called the Quadratic Arithmetic Program (CAP).
In this section, we describe how Alice can send a fairly short proof to Bob, showing that she has a valid assignment set for CAP. We will use the Pinocchio Protocol developed by Parno, Howell, Gentry and Raykova (Bryan Parno, Jon Howell, Craig Gentry, Mariana Raykova).
As given above, Alice wants to prove that she has a valid assignment set, which has some additional restrictions, for example . But we will not take this into account here and, for simplicity, we will show how easy it is to prove knowledge of some admissible assignment set.
If Alice has a valid assignment set, it means that if you define as described above, then there exists a certain polynomial H such that . In particular, for any we have .
Suppose now that Alice has no valid assignment set, but she also defines from some invalid set . Then you can be sure that T does not divide P. This means that for any polynomial H in the order not higher than d , P and will be different polynomials. Note that P and there are no higher order .
For the proof, we use the well-known Schwarz-Zippel lemma, which states that two different polynomials of degree not higher than may intersect at most points . Thus, if p is much larger the probability that for a random selection insignificant.
Based on this, you can create the following protocol sketch to check whether Alice has a valid assignment set:
Repeating again, if Alice does not have a valid assignment set, she will eventually use polynomials with which the required equality for the majority of randomly chosen s will not hold. Therefore, Bob is more likely to reject Alice’s answer, regardless of the chosen s .
Let's think, do we have the tools to implement this sketch? An important point is the choice of Alice polynomials, which she will use, while not knowing s . But this is exactly the problem that we solved in a reliable blind calculation of polynomials described in the previous article .
Given this, there are still four main points that need to be resolved in order to turn this sketch into a zk-SNARK. The first two we will look at in this article, and the other two in the final article.
Important point: if Alice does not have a valid assignment set, this does not mean that she cannot find any polynomials. order not higher than d , for which . It simply means that it cannot find such polynomials where and were “derived from an assignment set”; namely, that $ inline $ L: = Σ ^ m_ {i = 1} c_i⋅ L_i, R: = Σ ^ m_ {i = 1} c_i⋅ R_i, O: = Σ ^ m_ {i = 1} c_i⋅ O_i $ inline $ for recruitment .
The protocol above only ensures that it uses some polynomials. proper order, but does not guarantee that they were created from a valid assignment set. The formal proof is somewhat complicated, so we will give an approximate solution.
Let's combine polynomials in one polynomial F as follows:
The meaning of multiplying R by and o on in "not mixing" coefficients in f . Coefficients in F correspond to L , the following coefficients correspond to R , and the last coefficients correspond to O.
Combine the polynomials in the definition of the CAP in a similar way, defining for each polynomial whose first coefficients are coefficients and then the coefficients and then . That is for everyone we define a polynomial:
Note that when we sum two then and "Summed separately." For example, .
More generally, suppose we have for some set . Then we also get $ inline $ L = Σ ^ m_ {i = 1} c_i⋅ L_i, R = Σ ^ m_ {i = 1} c_i⋅ R_i, O = Σ ^ m_ {i = 1} c_i⋅ O_i $ inline $ for the same coefficients . In other words, if F is a linear combination it means that were really created from the set.
Therefore, Bob will ask Alice to prove to him that F is a linear combination from . This is done similarly to the protocol for reliable calculation:
Bob chooses random and sends Alice to hide $ inline $ E (β⋅ F_1 (s)), ..., E (β⋅ F_m (s)) $ inline $ . He then asks Alice to send him a hide. . If she succeeds, the expanded version of Accepted Coefficient knowledge suggests that she knows how to create F , which is a linear combination of .
In zk-SNARK, Alice wants to hide all the information about her set assignment. However hide provide some information about recruiting.
For example, given some other satisfying assignment set Bob can calculate the corresponding and hide . If they are different from Alice’s answer, he can understand that not Alice's assignment set.
To avoid such leakage of information about its set, Alice hides her set by adding a “random T- offset” for each polynomial, i.e. chooses random $ inline $ δ_1, δ_2, δ_3∈ F ^ * _ p $ inline $ and determines $ inline $ L_z: = L + δ_1⋅ T, R_z: = R + δ_2 T, O_z: = O + δ_3⋅ T $ inline $ .
Let's pretend that were obtained from a satisfying set of assignments. Consequently for some polynomial H. Since we just added a multiple of T everywhere, T also divides . Let's see this:
$ inline $ L_z⋅ R_z- O_z = (L + δ_1⋅ T) (R + δ_2⋅ T) - (O + δ_3 T) $ inline $ $ inline $ = (L ⋅ R - O) + L ⋅ δ_2⋅ T + δ_1⋅ T⋅ R + δ_1δ_2⋅ T ^ 2- δ_3⋅ T $ inline $ $ inline $ = T⋅ (H + L ⋅ δ_2 + δ_1⋅ R + δ_1δ_2⋅ T- δ_3) $ inline $
Thus, defining $ inline $ H_z = H + L ⋅ δ_2 + δ_1⋅ R + δ_1δ_2⋅ T- δ_3 $ inline $ get . Therefore, if Alice uses polynomials instead , Bob will always accept her answer.
On the other hand, these polynomials, calculated at provided that (which is almost always for all d and s ), do not contain any information about the valid assignment set. For example, non-zero and is random. Then is a random value, so will not contain any information about because it is “masked” by this random value.
We approximately showed the Pinocchio protocol scheme, in which Alice can convince Bob that she has a valid assignment set for the CAP, without disclosing information about this set. But there are still two important issues that need to be addressed to get the zk-SNARK:
Both of these issues can be solved using pairs of elliptic curves, which we will discuss in the final part.
Next article: Explaining SNARKs. Mating elliptic curves (translation)
Source: https://z.cash/blog/snark-explain5.html
Previous articles:
')
Part 1: Explaining SNARKs. Homomorphic hiding and blind computation of polynomials (translation)
Part 2: Explaining SNARKs. Knowledge of the adopted coefficient and reliable blind calculation of polynomials (translation)
Introduction from the translator
Starting the final part of the translation, I want to say that we live in a truly amazing time. The time when higher mathematics has the ability to almost immediately be involved in software development and we can observe “in action” the results of the work of mathematicians of technological institutes in advanced things based on blockchains and data exchanges.
Well, I will not detain further your attention, let's move on to the most interesting ...
From calculations to polynomials
In previous articles we have developed a specific mechanism for working with polynomials. In this part, we will learn how to transform the statements we want to prove and verify in the language of polynomials. The idea of using polynomials in this way begins with the pioneering work of 1991 by Lund, Fortwon, Karloff and Nisan (Carsten Lund, Lance Fortnow, Howard Karloff - University of Chicago AND Noam Nisan - Hebrew University).
In 2013, another yet another breakthrough work by Gennaro, Gentry, Parno and Raikova (Rosario Gennaro, Craig Gentry, Bryan Parno, Mariana Raykova) comes out. This work identified extremely convenient transformations of computations into polynomials called the Quadratic Arithmetic Program (QAP). KAP became the basis for modern zk-SNARK constructions, in particular, those used in ZCash cryptocurrency.
In the first part of the article, the transformations of the calculations in the CAP will be explained by example. Even if you focus on a small example, and not on a general definition, you have to spend enough time to understand it to begin with. So be prepared for a certain mental effort :)
Suppose Alice wants to prove to Bob that he knows such that . The first step is to present the calculation with in the form of an arithmetic circuit.
Arithmetic schemes
An arithmetic circuit consists of calculated arithmetic operations, called transitions, such as addition and multiplication, with connections between them. In our case, the scheme looks like this:

The bottom connectors are input parameters, and the top output connection is the result of calculating the entire circuit for these input parameters.
As can be seen in the figure, connectors and transitions of the circuit are designated in a certain way. These rules will be necessary for the next step, namely the transfer of the scheme in the CAP:
- When the same outgoing connector goes to more than one transition, it is considered that it is the same connector — for example, in the example.
- It is assumed that multiplication blocks have exactly two inputs, which are called left and right connectors.
- Connectors from addition to multiplication or addition are not marked. It is believed that the input parameters of the transitions of addition go directly to the transition multiplication. In the example it is considered that and are inputs
A valid assignment set for the scheme is the assignment of values for labeled transitions, where the output value of each multiplication transition is the result of the product of the corresponding inputs.
So, for our scheme, the valid assignment set is: Where and
Following this terminology, Alice wants to prove that she knows a valid assignment set such that . The next step is to translate this statement into a polynomial using CAP.
CAP
Each transition multiplication must be correlated with the field element: will be correlated with and with . We call the points {1, 2} our target points . Now we need to define a set of "left connecting polynomials" , "Right connective polynomials" and "output connecting polynomials" .
The main idea of this action is to ensure that the values of the polynomials are zero at all target points, except the target point of the multiplication transition, in which they are involved.
Speaking specifically, since left, right and output connectors respectively can define since the polynomial equals one at point 1 corresponding and is zero at point 2 corresponding .
notice, that and both are right inputs . Therefore, similarly, we define , because equals one at target point 2 corresponding and zero at another target point.
Denote all other polynomials as zero polynomials.
With fixed values they are used as coefficients for determining the left, right, and output "total" polynomials. That is, you can determine:
$ inline $ L: = Σ ^ 5_ {i = 1} c_i⋅L_i, R: = Σ ^ 5_ {i = 1} c_i⋅R_i, O: = Σ ^ 5_ {i = 1} c_i⋅O_i $ inline $
Then we define the polynomial
Now, after all these definitions, we can form a central definition: is a valid scheme assignment set if and only if P takes a zero value at all target points.
Let's see this using our example. Suppose that were defined as stated above with some . Let's calculate all these polynomials at target point 1 :
Of all only is non-zero at point 1 . So, . Similarly, we get and .
Consequently, . Similar can be obtained .
In other words, P vanishes at target points if and only if is a valid assignment set.
Now we will use the following algebraic fact: for the polynomial P and the point we have if and only if the polynomial divides P without remainder, i.e. for some polynomial H.
Having determined the target polynomial in this way: , we obtain that T divides P if and only if is a valid assignment set.
Based on the foregoing, we define the CAP as follows:
The quadratic arithmetic program Q of order d and size m consists of polynomials and the target polynomial T of order d .
Assignment Set satisfies Q if, defining $ inline $ L: = Σ ^ m_ {i = 1} c_i ⋅ L_i, R: = Σ ^ m_ {i = 1} c_i⋅ R_i, O: = Σ ^ m_ {i = 1} c_i⋅ O_i $ inline $ and , there exists T , which divides without remainder P.
Following this terminology, Alice wants to prove that she knows the set of assignments satisfying the CAP defined above, where ,
Let's summarize this part. We saw a statement like "I know such that »Can be translated into an equivalent statement about polynomials using CAP. Next, we will look at an efficient protocol for confirming knowledge of a valid set of CAP assignments.
Above, we tried to give a fairly short example of the cast in the CAP. We also recommend an excellent post by Vitalik Buterin for more detailed information on the program conversion to CAP.
Pinocchio Protocol
Earlier, we showed that the statement that Alice wants to prove to Bob can be transformed into an equivalent form in the "language of polynomials," called the Quadratic Arithmetic Program (CAP).
In this section, we describe how Alice can send a fairly short proof to Bob, showing that she has a valid assignment set for CAP. We will use the Pinocchio Protocol developed by Parno, Howell, Gentry and Raykova (Bryan Parno, Jon Howell, Craig Gentry, Mariana Raykova).
As given above, Alice wants to prove that she has a valid assignment set, which has some additional restrictions, for example . But we will not take this into account here and, for simplicity, we will show how easy it is to prove knowledge of some admissible assignment set.
If Alice has a valid assignment set, it means that if you define as described above, then there exists a certain polynomial H such that . In particular, for any we have .
Suppose now that Alice has no valid assignment set, but she also defines from some invalid set . Then you can be sure that T does not divide P. This means that for any polynomial H in the order not higher than d , P and will be different polynomials. Note that P and there are no higher order .
For the proof, we use the well-known Schwarz-Zippel lemma, which states that two different polynomials of degree not higher than may intersect at most points . Thus, if p is much larger the probability that for a random selection insignificant.
Based on this, you can create the following protocol sketch to check whether Alice has a valid assignment set:
- Alice selects polynomials order not higher than d .
- Bob picks a random point and calculates the hiding .
- Alice sends Bob a hide for these polynomials at point s , namely .
- Bob checks whether the required equality holds at s . That is, he checks
Repeating again, if Alice does not have a valid assignment set, she will eventually use polynomials with which the required equality for the majority of randomly chosen s will not hold. Therefore, Bob is more likely to reject Alice’s answer, regardless of the chosen s .
Let's think, do we have the tools to implement this sketch? An important point is the choice of Alice polynomials, which she will use, while not knowing s . But this is exactly the problem that we solved in a reliable blind calculation of polynomials described in the previous article .
Given this, there are still four main points that need to be resolved in order to turn this sketch into a zk-SNARK. The first two we will look at in this article, and the other two in the final article.
The confidence that Alice selects her polynomials according to the assignment set
Important point: if Alice does not have a valid assignment set, this does not mean that she cannot find any polynomials. order not higher than d , for which . It simply means that it cannot find such polynomials where and were “derived from an assignment set”; namely, that $ inline $ L: = Σ ^ m_ {i = 1} c_i⋅ L_i, R: = Σ ^ m_ {i = 1} c_i⋅ R_i, O: = Σ ^ m_ {i = 1} c_i⋅ O_i $ inline $ for recruitment .
The protocol above only ensures that it uses some polynomials. proper order, but does not guarantee that they were created from a valid assignment set. The formal proof is somewhat complicated, so we will give an approximate solution.
Let's combine polynomials in one polynomial F as follows:
The meaning of multiplying R by and o on in "not mixing" coefficients in f . Coefficients in F correspond to L , the following coefficients correspond to R , and the last coefficients correspond to O.
Combine the polynomials in the definition of the CAP in a similar way, defining for each polynomial whose first coefficients are coefficients and then the coefficients and then . That is for everyone we define a polynomial:
Note that when we sum two then and "Summed separately." For example, .
More generally, suppose we have for some set . Then we also get $ inline $ L = Σ ^ m_ {i = 1} c_i⋅ L_i, R = Σ ^ m_ {i = 1} c_i⋅ R_i, O = Σ ^ m_ {i = 1} c_i⋅ O_i $ inline $ for the same coefficients . In other words, if F is a linear combination it means that were really created from the set.
Therefore, Bob will ask Alice to prove to him that F is a linear combination from . This is done similarly to the protocol for reliable calculation:
Bob chooses random and sends Alice to hide $ inline $ E (β⋅ F_1 (s)), ..., E (β⋅ F_m (s)) $ inline $ . He then asks Alice to send him a hide. . If she succeeds, the expanded version of Accepted Coefficient knowledge suggests that she knows how to create F , which is a linear combination of .
Adding the “Zero Disclosure” Part - Hiding the Assignment Set
In zk-SNARK, Alice wants to hide all the information about her set assignment. However hide provide some information about recruiting.
For example, given some other satisfying assignment set Bob can calculate the corresponding and hide . If they are different from Alice’s answer, he can understand that not Alice's assignment set.
To avoid such leakage of information about its set, Alice hides her set by adding a “random T- offset” for each polynomial, i.e. chooses random $ inline $ δ_1, δ_2, δ_3∈ F ^ * _ p $ inline $ and determines $ inline $ L_z: = L + δ_1⋅ T, R_z: = R + δ_2 T, O_z: = O + δ_3⋅ T $ inline $ .
Let's pretend that were obtained from a satisfying set of assignments. Consequently for some polynomial H. Since we just added a multiple of T everywhere, T also divides . Let's see this:
$ inline $ L_z⋅ R_z- O_z = (L + δ_1⋅ T) (R + δ_2⋅ T) - (O + δ_3 T) $ inline $ $ inline $ = (L ⋅ R - O) + L ⋅ δ_2⋅ T + δ_1⋅ T⋅ R + δ_1δ_2⋅ T ^ 2- δ_3⋅ T $ inline $ $ inline $ = T⋅ (H + L ⋅ δ_2 + δ_1⋅ R + δ_1δ_2⋅ T- δ_3) $ inline $
Thus, defining $ inline $ H_z = H + L ⋅ δ_2 + δ_1⋅ R + δ_1δ_2⋅ T- δ_3 $ inline $ get . Therefore, if Alice uses polynomials instead , Bob will always accept her answer.
On the other hand, these polynomials, calculated at provided that (which is almost always for all d and s ), do not contain any information about the valid assignment set. For example, non-zero and is random. Then is a random value, so will not contain any information about because it is “masked” by this random value.
What is left to consider in the final part?
We approximately showed the Pinocchio protocol scheme, in which Alice can convince Bob that she has a valid assignment set for the CAP, without disclosing information about this set. But there are still two important issues that need to be addressed to get the zk-SNARK:
- In the scheme, Bob needs the polynomial H , which "supports multiplication." For example, he needs to calculate the hiding of and . However, we have not yet considered examples of H , which allows this. We considered only H , which supports addition and linear combinations.
- We also discussed interactive protocols between Alice and Bob. However, our ultimate goal is to allow Alice to send non-interactive evidence in one message. These messages are publicly available. This means that anyone who sees this “message - proof” can also be convinced of its authenticity, and not just Bob (who previously interacted with Alice).
Both of these issues can be solved using pairs of elliptic curves, which we will discuss in the final part.
Next article: Explaining SNARKs. Mating elliptic curves (translation)
Source: https://habr.com/ru/post/343954/
All Articles