A couple of months ago, an interesting article appeared with an analysis of the classical problem of placing queens on a chessboard (see details and history below). The task is incredibly well known and everything has already been examined under a microscope, so it was surprising that something really new had appeared.

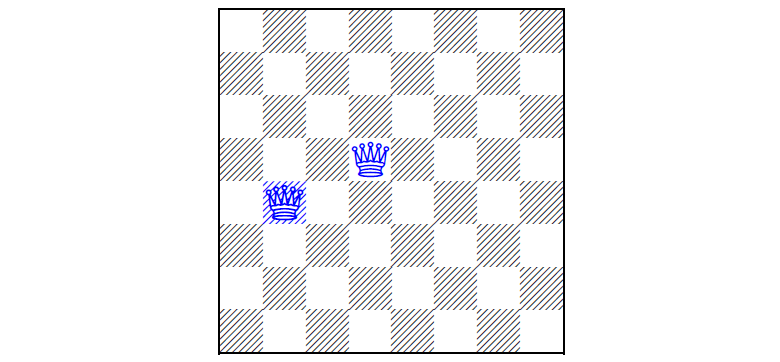
Can you put six more? And find all the solutions?
(picture from the article)

Further, unfortunately, there was some completely unintelligible story from the chain of such transformations:

• Excellent article --- University press service ---> unintelligible press release .
• Press release --- amusing translation ---> incomprehensible article on Hyktimes

It is worth noting that five at random open links in Russian even less clarified the picture of what is happening.

I thought here - it would be necessary for someone to interrupt this strange chain and state the essence of events in a normal language.

What will be discussed:

• Task history
  
  • Latin square
  • The eight queens problem
• Three types of "queens" problem
  
  • Arrangement of N Queens
  • Count the number of decisions
  • Addition to N Queens
  • Task variations
• Models and complexity
  
  • Linear Search for N Queens
  • How to count the number of solutions in practice
  • Supplement to N
• findings
  
  

  Task history

  
  
  

  Latin square

  
  

  The task has been known since antiquity ( ~ the Middle Ages ), it is necessary to arrange the letters so that in one line and in one column they are not the same, as for example here:
  

  
  
  
  The name Latin Square itself received due to the habit of using Latin letters by Leonard Euler for this task. From the Latin square (and a number of similar problems), new ones naturally appeared, such as the problem of queens, where an additional constraint on the diagonal is added.
  
  

  The eight queens problem

The task was invented in 1848 by chess composer Max Bezsel: the essence of the task is to arrange 8 queens on a chessboard so that they do not attack each other. Since then, many mathematicians, such as Gauss, have been working on the problem, and algorithmic scientists and programmers, such as Dijkstra, have come up with many approaches to finding and counting solutions.

In the problem we are going to talk about, not 8 queens, but N and the board, respectively, are not ordinary chess, but NxN.

Three types of "queens" problem

There are three most popular queen problem statements.

Arrangement of N Queens

The task is formulated very straightforwardly.

Given : empty NxN board, for example 8x8

(in principle, it is clear that simply specify N, but so clearer)

Find : Arrangement of the maximum possible number of queens

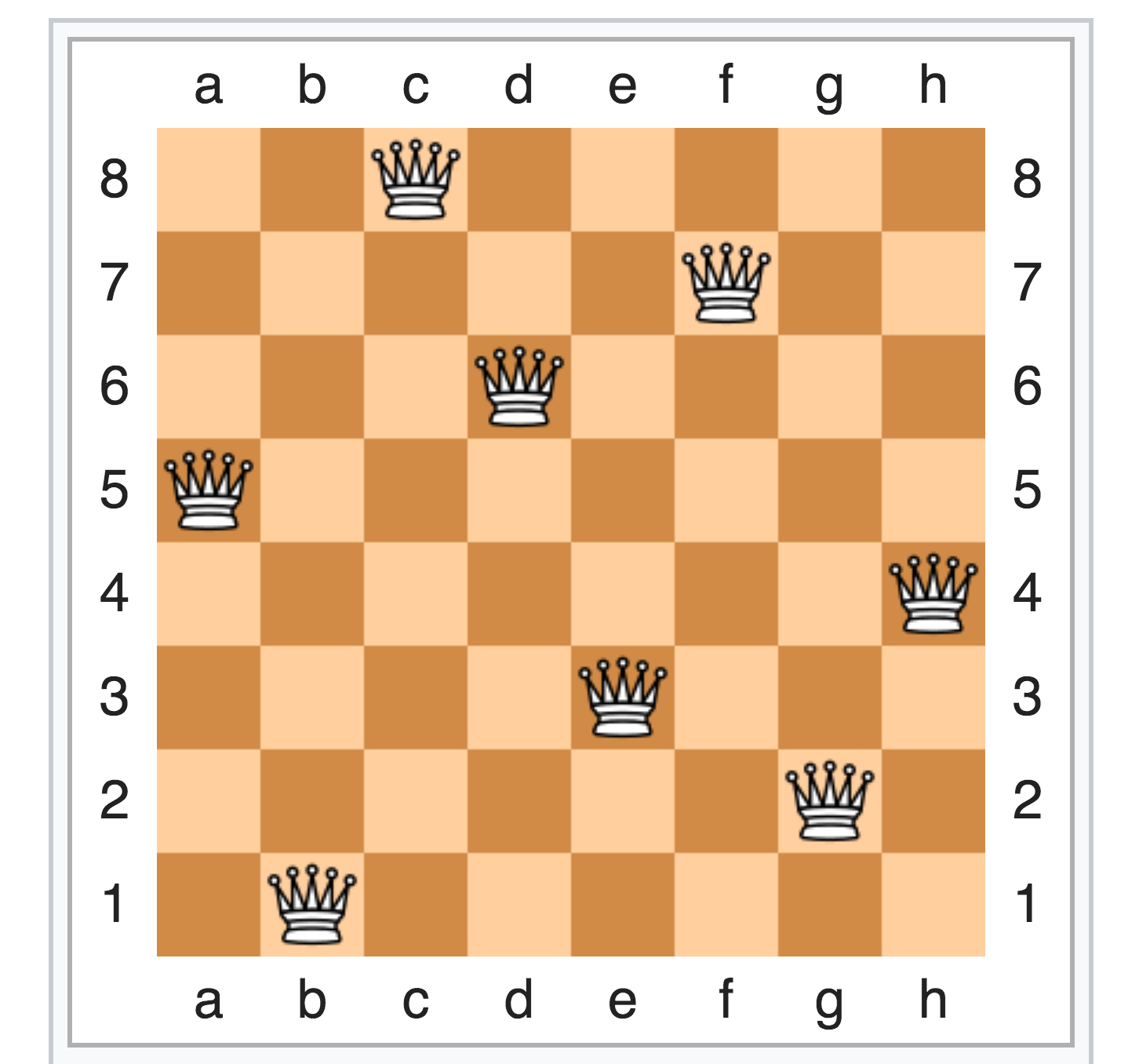
Those. at the input the number is the size of the board, and at the exit the position of queens (one solution).

Count the number of decisions

The task is also quite simple:

Given: size of empty board N
Find: H is the number of possible arrangements of N queens on the board.

For example, the size of the board is N = 1, then the number of possible arrangements is H = 1.
N = 8 => H = 92.

Addition to N Queens

Here the wording is a bit more insidious:

Given: board size N and M positions of already established queens
Find: Positions Remaining N - M Queens

Visually, everything is like on KPDV:

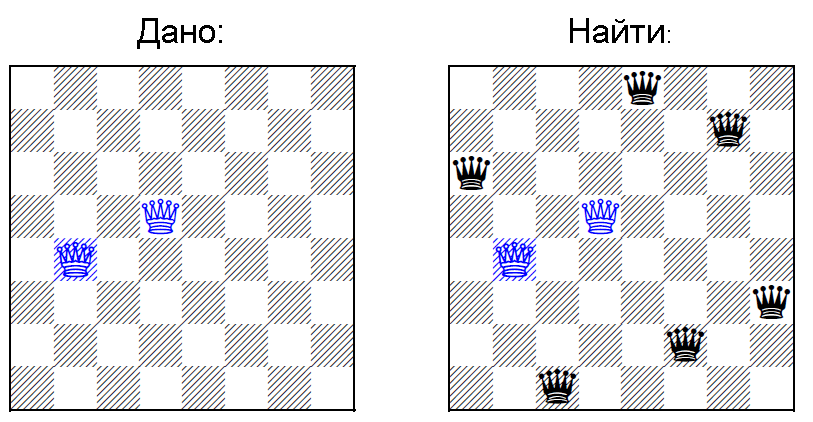
(picture is also from the original article)

Task variations

Generally speaking, there are more variations of the problem: see for example: the arrangement of white and black queens
http://www.csplib.org/Problems/prob110
however, here we consider only the main classic version.

In such a variation, the solutions are significantly different (White does not beat White, and Black does not Black: in case of confusion, see the comments here ):

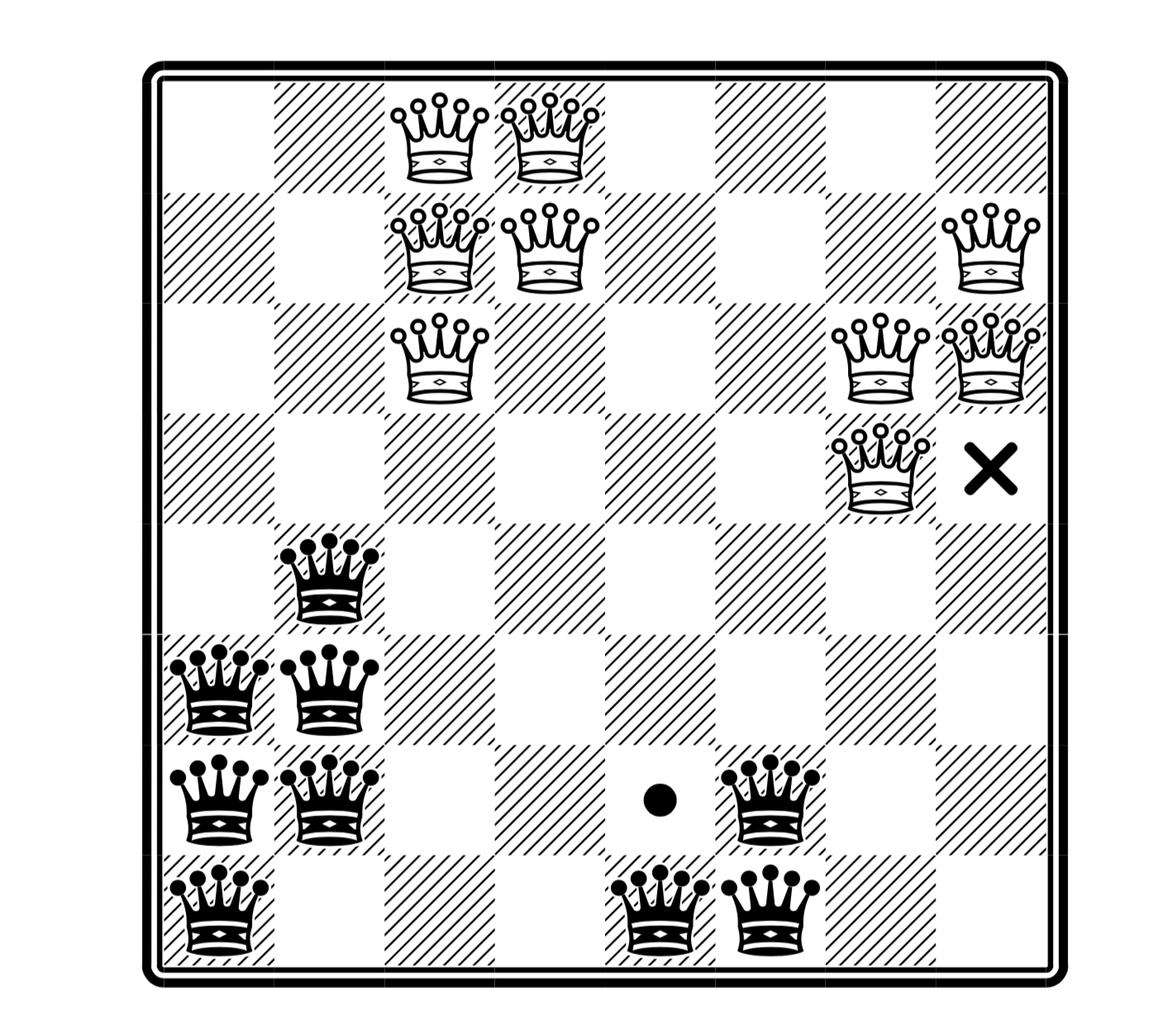
(here is the maximum number of queens, and in the place of the cross you can put white, and in place of the black point - but not both at once; taken from the article )

Models and complexity of tasks

The time has come to actually discuss: how does this decide everything and how quickly can this be done at all?

Linear search for a classic task

The most interesting point is that even experts sometimes get confused and think that to solve the N-queens, a combinatorial search is needed and they think that the complexity of the problem is higher than P. About the fact that P and NP are once wrote on Habré: Why do we all need SAT and all these P-NP (part one) and the second here . However, the problem is solved without going through the options! That is, for a board of any size, you can always arrange the queens one by one in the following ladder:

There are a number of alignment algorithms, for example, see this article or even here in the wiki .

Hence the conclusion, for N = 1 and N> 3 there is always a solution (see algo), and for N = 2 or N = 3
always not (trivially follows from the board). This means that the solvability problem for N queens (where you need to say if there is a solution or not) is solved trivially in a constant time (well, ok, constructively linear - to arrange / check).

It's time to double-check what we read, we read the typical title “the N Queens problem was recognized as an NP-complete task” - did you have your eyes flush?

How to count the number of solutions in practice

This is where the most interesting begins: the number of solutions for the queens placement problem even has its own name - “ A000170 sequence”. This is where the good news ends. The complexity of the problem: above NP and P #, in practice this means that the optimal solution is to download the sequence data to the dictionary and return the desired number. Since for N = 27 it was already considered on a parallel cluster for how many weeks there.

Solution : write out a label and n, return a (n)
na (n)
eleven
20
thirty
4: 2
5:10
6-4
7:40
8: 92
9: 352
10: 724
...
21: 314666222712
22: 2691008701644
23: 24233937684440
24: 227514171973736
25: 2207893435808352
26 22317699616364044
27: 234907967154122528

However, if you have some tricky version of the problem and still need to calculate the solutions (and their number is unknown and no one considered them before), then the best version of the prototype is discussed below.

Addition to N and Answer Set Programming

Here the most interesting begins: what is the new result of the article? The task of complementing to N queens is NP-complete ! (Interestingly, the NP-completeness of the Latin square addition was known as far back as 1984.)

What does this mean in practice? The easiest way to solve this problem (or suddenly, if we need its variation) is to use SAT. However, I prefer the following analogy:

SAT is an assembler for combinatorial NP-problems, and Answer Set Programming (ASP) is C ++ (the ASP also has a mysterious Russian soul: it is at times confused and unpredictable for the uninitiated; by the way, the theory underlying modern ASP has been invented in 1988, by Mikhail Gelfond and Vladimir Lifshits, then working at the universities of Texas and Stanford, respectively).

To put it simply, ASP is a declarative constraint programming language (constraints in English literature) with Prolog syntax. That is, we write down what constraints the solution must satisfy, and the system reduces everything to the SAT version and finds a solution for us.

The details of the solution are not so important here, and Answer Set Programming is worthy of a separate post (which is already indecently long in my draft): therefore, we’ll analyze conceptual points

% domain row(1..n). column(1..n). % alldifferent 1 { queen(X,Y) : column(Y) } 1 :- row(X). 1 { queen(X,Y) : row(X) } 1 :- column(Y). % remove conflicting answers :- queen(X1,Y1), queen(X2,Y2), X1 < X2, Y1 == Y2. :- queen(X1,Y1), queen(X2,Y2), X1 < X2, Y1 + X1 == Y2 + X2. :- queen(X1,Y1), queen(X2,Y2), X1 < X2, Y1 - X1 == Y2 - X2. 

Line 1 { queen(X,Y) : column(Y) } 1 :- row(X). - called the choice rule, and it determines what is a valid search space.

The last three lines are called integrity constraints: and they determine what constraints the solution should satisfy: there can be no queen in the same row, no queen in the same column (omitted due to symmetry) and no queen on the same diagonal.

As a system for experiments, I recommend Clingo .
And for starters, it is worth watching their tutorial and post a blog at www.hakank.org .

Of course, if you write on ASP for the first time, then the first model will not work incredibly efficient and fast, but most likely it will be faster to bust with a return written in haste. However, if you understand the basic principles of the system, ASP can become "regexp for NP-complete tasks."

Let's conduct a simple numerical experiment with our ASP model. I added 5 insidious queens to the model and ran a search for a solution for N from 1 to 150 and this is what happened (running on a regular home laptop):

')

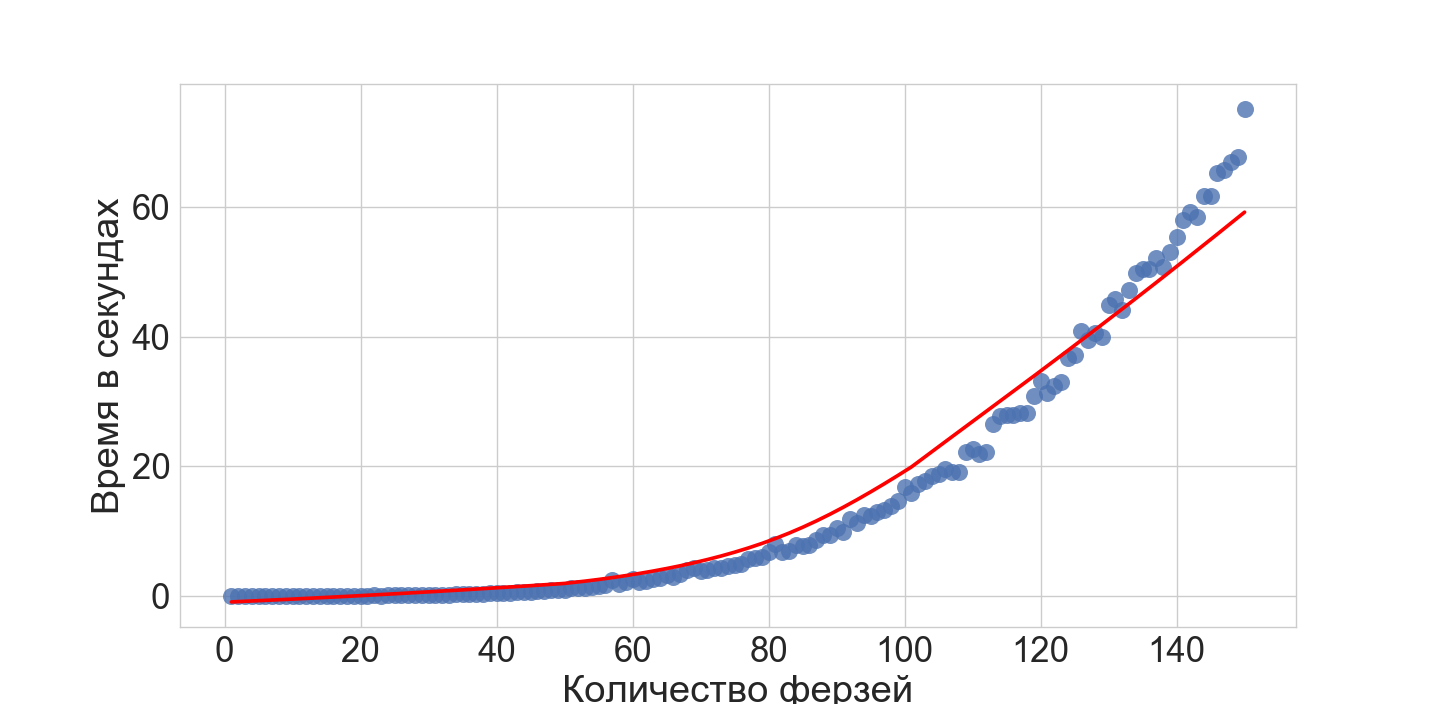
So, our ASP model can find solutions for the add-on problem for about a minute with N <= 150 (in the usual case). This shows that the system is excellent for prototyping models of complex combinatorial problems.

findings

• The new result is connected not with the classical problem of 8 queens, but with the addition of the generalized problem of queens (which is interesting, but on the whole is natural);
• The complexity increases significantly, because, by slyly putting the queens on the board, you can knock down an algorithm that puts the queens on some fixed pattern;
• It is impossible to effectively calculate the number of solutions (well, absolutely; until some horror happens and P is not equal to NP, etc.);
• Perhaps this result will affect the work of modern SAT systems, as some experts believe that this task is somewhat simpler than the classic NP-complete tasks (but this is just an opinion)
• If for some reason you need to solve a similar task for some reason, it is best to use the systems Alla Answer Set Programming, specially designed for this purpose.