Avtomatny workshop - 2. Example "Crossing", the mathematical transformations of TK in OA
Often, a successful subject image of the process that needs to be carried out is equivalent to obtaining a solution to the problem in general, this is almost half the success in choosing OA. This is so important that I want to illustrate what the objective view is meant by the term and how the choice of a successful OA naturally follows from a view of the subject, and already the choice of a successful OA pushes one to find the optimal solution. Thus, it is possible to put a sign of an approximate equality between the choice of the optimal OA and the determination of the optimal solution. In the last article I demonstrated the choice of OA on the example of the module "Display". Further work on the "Display" is another topic: the modification of auto-implemented programs , I will return to it a little later. Today's task still more clearly shows the procedure for developing an optimal OA.
Statement of the problem in the form of “wolf, goat and cabbage” is just an excuse, and we will focus on solving the problem in general, for any number of participants and their food addictions, and any number of places in boats. The task is to obtain such an algorithm that will allow us to find the shortest way to implement the crossing, or to show that the problem in this formulation has no solution.
')
Identical transformations TK
I will begin with the quotations from the previous article “there are cases when the subject image of the conditions of the problem does not even hint with what operational automaton to process them. In this case, the conditions of the problem can be subjected to mathematical processing, and to solve not the original problem, but a mathematically identical, but more convenient one ”.
Literally, the shipping process will consist of the following steps.

Figure 1. Initial presentation of the transport process
If you look at it as a mathematician, and completely abstract from the logistics of river transport, you can see that steps 1, 3, 5, 7 are superfluous. In those moments when the farmer is on the shore, there can be no problems, only cases need to be considered when the farmer is on the way. The case of a peasant moored to the shore simply means the exchange of the contents of the boat and the shore. The peasant in this case is strongly associated with the boat and it can no longer be considered at all. Since there are no excesses in the boat according to the condition of the problem, it can also not be considered at all, along with the contents. If something is currently in the boat, then there will be one smaller object on the banks. Everything described above created information noise, not allowing to see the essence of what is happening. In this case, the transportation process is depicted as shown in Fig. 2
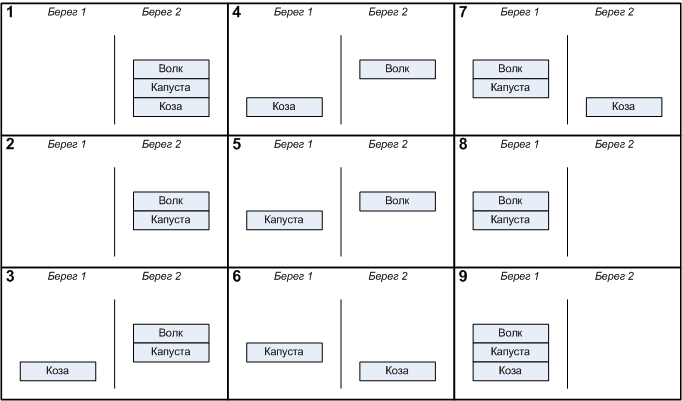
Figure 2. The process of transportation after identical transformations
The fact that I did this is essentially the same transformation. Mathematical experience and mathematical intuition help to see the identity of the tasks shown in Figures 1 and 2. Not so long ago there was a survey in which the author was interested in whether mathematics is necessary for programmers. In my experience, for the development of mathematical experience and intuition, I would strongly advise programmers to study probability theory. It is the theory of probability that teaches combinatorics, and the fact that it is necessary to take into account not only the variants of interest (called test outcomes ), but also all possible variants. This is actually a reinforcement of the advice from the previous article that “it is important to depict not only the ideal case, but also the“ inconvenient ”variants that are associated with the boundary conditions. ... Such an approach shifts the program development resources from the debugging stage (when dealing with a bunch of implemented modules) to the design phase (when dealing with a blank canvas). " In this case, the" convenient "and" inconvenient "options are not a direct reference to probability theory , we are talking about an appropriate way of thinking, which is remarkably trained by the mentioned section of mathematics. This is just a tip, you can not listen to him, as well as to the majority of tips in this world.
TK analysis
Since the task in its current form, as stated above, is rather trite, consider its more complex modification.
It is required to transport a goat, cabbage, a dog and a wolf in a boat from one bank to another. There are only two places in the boat (one for the peasant). It is known that if you leave a wolf alone with a dog, they will have “armed neutrality”, but if a goat remains with them, the carnivorous wolf will leap up, the dog will rush to goat protection, in general, the three of them cannot be left. How to transport?
I will say that the image of fig. 2 gives a consistent picture and does not give clarity, and this is its main drawback. To depict the problem in the form of a table - solution number 1, the best solution of all possible, because now all the outcomes of events at a glance. The row and column marked with the symbol 0 mean empty shore.
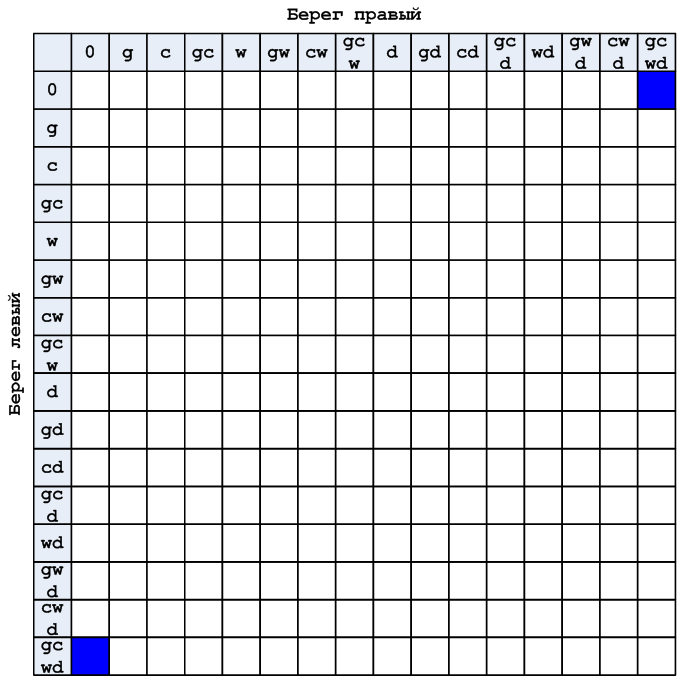
Figure 3. Object Image
This allows you to cover the whole picture, and connect the right hemisphere, which specializes in information processing, expressed not in words, but in symbols and images. The main area of specialization of the right hemisphere is intuition. Of course, one intuition is not enough, but for “techies”, intuition does not dominate logic, but complements it. With the right approach, the right hemisphere (creative, intuitive) will give food for thought to the left, which is responsible for logic and analyzes the facts obtained. Information is processed by the left hemisphere sequentially in stages. Since the whole cycle is dedicated to software automata, the following analogy fits into this channel: the right hemisphere can be compared with an operational machine that provides solutions, and the left hemisphere can be compared with the control machine that tests selected solutions, eliminates the invalid ones and gives the following task to the right one "Insight" gives the following thought. That is, to depict the task is essentially important in order for the right hemisphere, covering the whole picture, to have that food for thought that suits him better, and this in turn will allow to generate more relevant trial solutions that will become food for thought to the left hemisphere.
Image pic. 3 is mathematically identical to the image of the problem, which is shown in Fig. 2, and it in turn is identical to the complete step-by-step process image with loading and unloading similar to that shown in Figure 1.
With this image, the task is reduced to finding a path from the lower left to the upper right square, which are marked in blue. However, not all combinations (intersections of columns and rows) are valid. For example, a combination marked with a cross cannot exist, because in this situation the goat ends up on two banks at once.
Figure 4. Splitting characters
If we exclude all situations associated with bifurcation, the number of remaining options is significantly less.
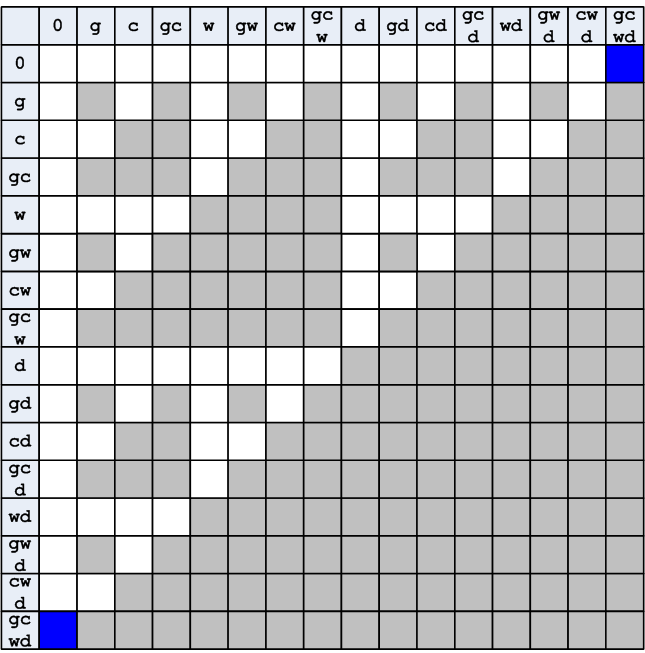
Figure 5. Elimination of splitting situations
The next step, dictated by logic, is to remove states like the one shown in fig. 6. The meaning of this is that one goat on the left bank and no one on the right means (if we exclude the fact that the wolf ran into the forest), that there are cabbage and a wolf in addition to the peasant in the boat. But according to the conditions of the problem in the boat one place.
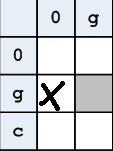
Figure 6. Boat overload
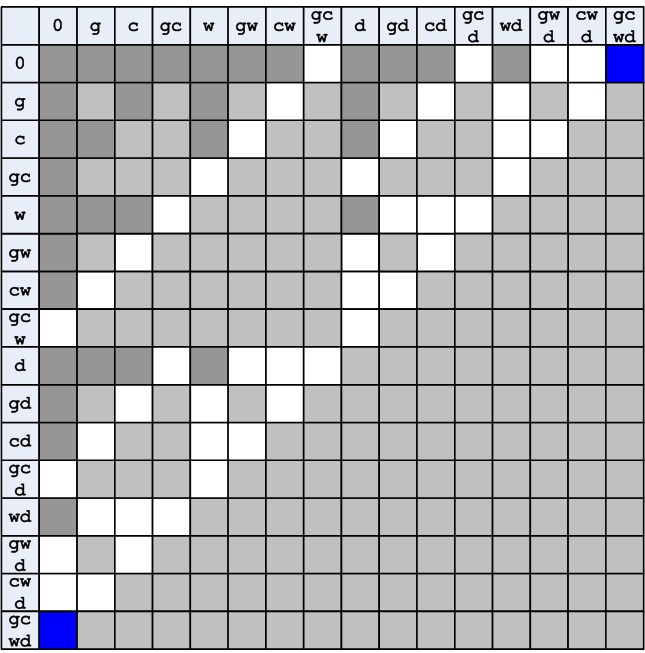
Figure 7. Exclusion of situations with boat overload
There are variations of this task when the boat has two passenger seats. Such varieties are identical to the variant being solved, just in this case there will be a smaller number of cells excluded by overloading.
Next, you need to exclude all prohibited situations associated with eating some characters by others.
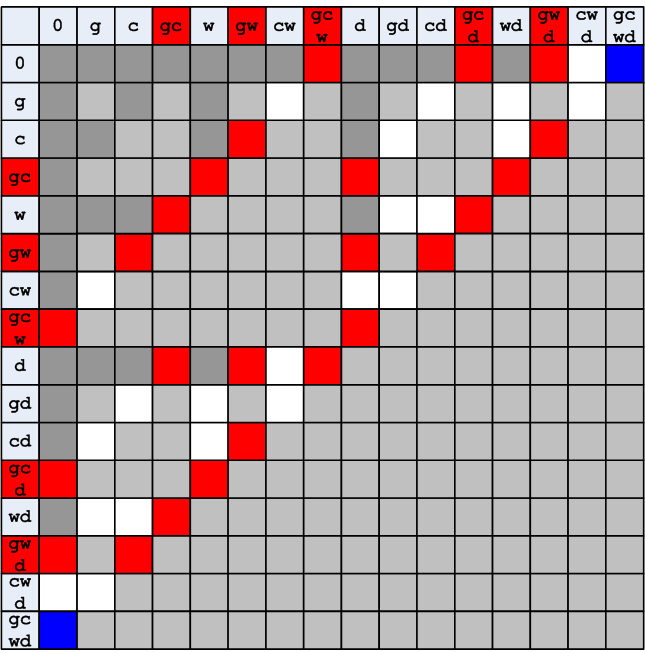
Figure 8. Exclusion of prohibited states
It is impossible to further reduce the number of cells, all remaining states are allowed. But how to use this table?
You can see that the movement along the vertical is associated with the manipulation of objects on the left bank, and the movement horizontally is associated with the manipulation of objects on the right bank. For example, the movement shown by the arrow means unloading cabbage from the boat (on the left bank) and loading a wolf. Goat on the right bank.
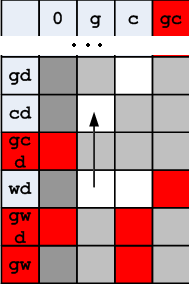
Figure 9. Explanations for the manipulation of objects
At the same time, it is possible to move to any number of cells horizontally or vertically, but it is not allowed to move diagonally.
This is the operating machine. If you do not take the word “machine” literally, then OA is a method of processing, a scheme for manipulating data, objects, etc. In this case, OA is a table from which all “impossible” and inadmissible states are removed, in which you can move vertically or horizontally. Now it remains only to find the shortest path in this labyrinth, and this is exactly what the control machine will do.
I’ll express the idea that programmers often view programming languages as an intermediate language into which you want to translate the original TZ written in human language before the compiler translates it into machine language. For many problems, such an approach is indeed justified and natural, but only when manipulations with OA are described by an obvious sequence of actions, for example:
1. Read data from the Edit window.
2. Convert text to function coefficients.
3. Plot the function on the Chart.
However, in this case, an attempt to find a solution to the original TK, literally embodying the conditions of the problem, would lead to approximately the following sequence of actions:
1. Get another character,
2. To transport, to the other side,
3. If you can't leave him there, pick up another character and bring him back. go to step 1.
Despite the fact that even a child armed with a pencil can perform the task of finding a way in the labyrinth shown in Fig. 8, if solved using the above method, a parallelization of the problem can occur at any stage, since you can take one character or another case will be its own scenario of subsequent events. Such an approach is really fraught with recursion with increasing computational complexity.
A few words about the computational complexity of such a solution. For this task, a full search is not a traversal of the entire table, because a full search for this task implies not just going through all possible combinations, but all possible sequences for all possible combinations .
Control machine.
The resulting scheme assumes a simple algorithm for finding the path.
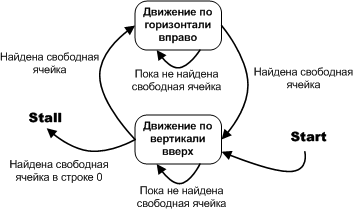
Figure 10. Pathfinding algorithm in the maze without dead ends and cycles
However, presumably such an option is possible that a movement down or to the right is required (for example, when solving this task) . I will use my own advice "to consider inconvenient cases."

Figure 11. An example, with the need for multidirectional movement when bypassing free cells
To eliminate the objection that the real lower right subdiagonal half should be completely excluded by the rule of duplication of characters, suppose that this is just a fragment from the upper half diagonal and there are no more free cells in the whole table.
Such a maze is not circumvented if you move all the time up or to the right. Obviously, a serious path finding algorithm is needed here. Search for the path "in the forehead" for the version of fig. 11 will lead to enumeration of all possible paths, and although the number of combinations is relatively small, this is fraught with recursion again and has the same disadvantages as the full brute force option. It is better to use the so-called. wave algorithm or Lie algorithm. I will not describe it here, you can quickly glance at the link.
Let us return, however, to the crossing, fig. 8. Wave propagation starts from the upper right corner, which is assigned the number 0. Note that a vertical search downwards for this column is not possible, since all cells in this column are excluded by the duplication rule. The only possible movement is to the left. There is only one “white” cell in the row. Mark it with the number 1. After this, cell 2 is marked in the same way.
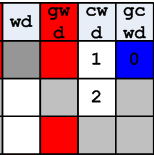
Figure 12. The first two steps of the wave calculation.
Next, an important point. From the cell labeled 2, you can move to any of the cells horizontally in one move, all of them should be marked with the number 3.

Figure 13. Equivalent cells
The consistent application of this algorithm results in the following picture.
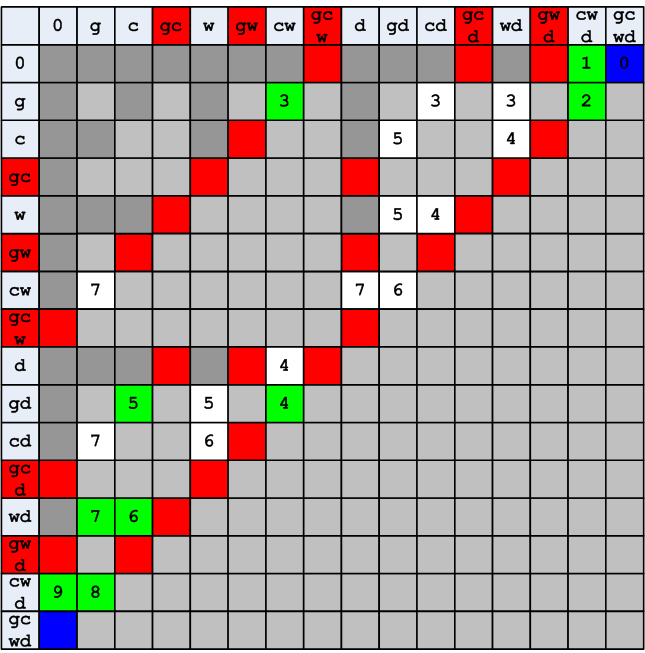
Figure 14. The labeled field for finding the shortest path, and the path found (green cells)
The criterion for successful completion of the search - in the vertical with the index 0 there must be at least one "uncollected" cell, and it must be marked with a number. The search for the path is conducted in the classical way: being in each cell, the next cell is searched (in our case, any in the same row or in the same column), which has a smaller number. The cells that make up the path are highlighted in green.
Using my own advice to consider uncomfortable options, I propose to consider an illustration
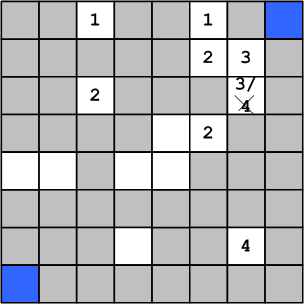
Figure 15. Ambiguity
In this case, it seems that when going around the maze in different ways, a contradiction arises. However, in fact, there is no contradiction, it is enough to put the numbers only in the cells that are not yet occupied. Then, bypassing the path that would lead to the value 4, the disputed cell already contains 3 and simply does not get into consideration.
One of the options for constructing a wave involves the recursive nature of the algorithm for sorting points. However, I offer another solution. It allows you to do without recursion, and is based on the following rationalization.
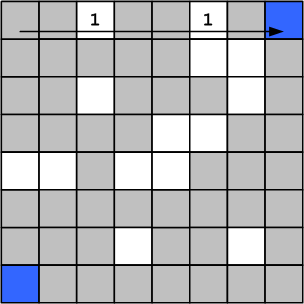
Figure 16. Wave calculation step 1
The wave calculation will consist of alternating bypassing the rows and bypassing the columns. The review starts from the top row, in which all cells are placed 1. Next, the row is re-run (“search” stage), and for each cell containing 1, a cycle is held down the column (“scan-fill” stage), during which all free cells are marked with a number 1 larger than the previous one.
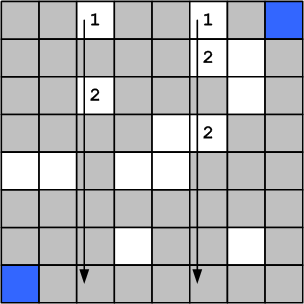
Figure 17. Wave calculation step 2
After that, the columns and rows are swapped, and now the columns containing the number 2 are searched , and the corresponding row is scanned from each column.

Figure 18. Wave calculation step 3
This operation is repeated until at least one cell in column 0 is marked. Given that there may not be a complete traversal path, the traversal is stopped if at the next traversal (search + scanfill) none are found new cell.

Figure 19. The result of building a wave
With such a detour, each line is traversed 2 times - during the search and during the scan-fill . More precisely, since after scanning horizontally, scanning begins vertically, it would be better to list in a different order: during the scan-fill and during the subsequent search .
But since at the time of each iteration it is not known which line contains a number, for example 3, and which does not contain it, to search for each line you need to look through all the lines, and this leads to the fact that each line is viewed once during the search for number 3 and more many times when searching for the remaining numbers (which are not there).
I draw your attention that the “search + scan-fill” iterations alternate for rows and columns, so during the search in rows, even ones will not be searched for, and vice versa. In this case, the number of views of each cell is reduced by half.
But pay attention to one characteristic thing. By the fill algorithm, each line will have the form.
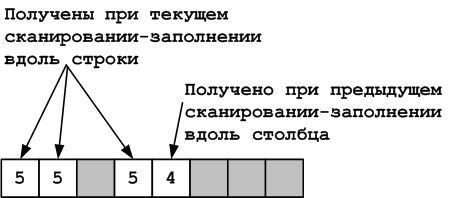
Figure 20. Typical row contents
I pay attention that the algorithm is not recursive. If it were recursive, it would mean that one path is explored to a maximum depth, after which the algorithm goes back (one position at a time, but it may turn out that it goes to the very beginning), after which the next path is explored. As a result of this kind of crawling, adding numbers to the table does not go in ascending order, but lower numbers can be added to a field that is already full of higher ones.
When traversing the table in the manner described above, each row will contain a number
N-1 obtained by scanning-filling the previous iteration, and the number N that will be entered into it when scanning-filling the current iteration. Moreover, the N-1 numbers may be several, due to the fact that each iteration implies scanning-filling a number of lines, but there will not be a single number in the line other than N-1 , N.
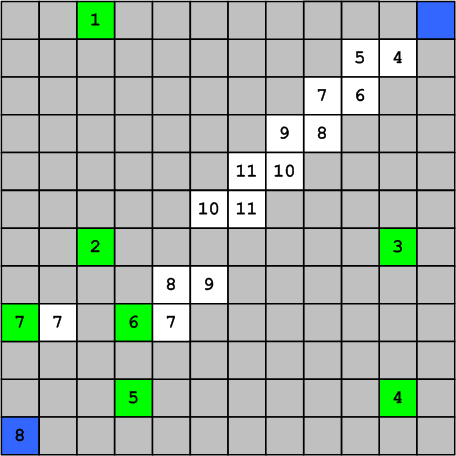
Figure 21. Illustration of the features for filling rows and columns
Moreover, in the case of fig. 20, the number 4 refers not to the row, but to the column, so if we consider only the numbers related to the row, it turns out that the row contains only numbers 5. The situation is similar with the columns.
This is more than just observation; this is the basis for further development. Illustrated rice. The 16-19 algorithm implies a preview of the cells of each row in order to determine whether it contains the required number (for example, for Fig. 21 we take the search for the number 7). Given that the lines contain a pair of numbers N-1 and N, you can stop viewing the first line by reaching the cell with the unit. The second line can also not be considered to the end, having met the number 5, but it will have to be scrolled almost to the end. At the same time, since, as I have shown, only one number is associated with each filled row and one number with each column, the task can be interpreted as follows. In addition to the table, a pair of arrays is created - one for the rows and one for the columns.
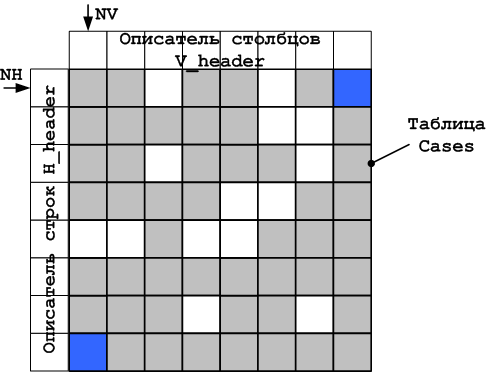
Figure 22. OA wave construction
Since you can only move horizontally from the upper right blue square (the entire vertical line is excluded by the duplication rule), the search starts from the line marked by the NH arrow. In cell H_header[0] 1 is entered during initialization. The following is the procedure that can be described by the state diagram shown in Figure. 23
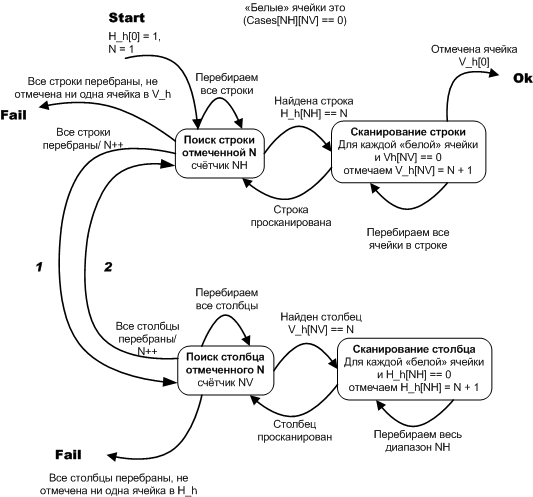
Figure 23. Wave construction algorithm
Why do I think that the state diagram is an alternative, more convenient form of writing software algorithms? It is a convenient tool for “shorthanding” of thoughts, as they come to mind, because it is built from identical blocks that can be connected with any imaginable lines.
How to create an algorithm according to this diagram? In general, elementary, even simpler and more mechanistic than if I described everything in words. Those actions that are marked as iterate ... correspond to the cycles, the remaining arrows are conditions, the arrows on the left, labeled 1 and 2 imply a while(1) .
uint tCalculator::Make_wave() { u1x N = 1; Horizontals_header[0] = 1; while(1) { //////////////////////////// // bool Found = false; for(u1x Horizontal_N = 0; Horizontal_N < Line_size; Horizontal_N++) { if(Horizontals_header[Horizontal_N] == N) { //////////////////////////// // for(u1x Vertical_N = 0; Vertical_N < Line_size; Vertical_N++) { if( (Cases_table[Horizontal_N * Line_size + Vertical_N] == 0) && (Verticals_header[Vertical_N] == 0 ) ) { Found = true; Verticals_header[Vertical_N] = N + 1; if( Vertical_N == 0 ) return(N+1); } }//for(u1x Vertical_N = 0; Vertical_N < Line_size; Vertical_N++) }//if(Horizontals_header[Horizontal_N] == N) }//for(u1x Horizontal_N = 0; Horizontal_N < Line_size; Horizontal_N++) if(!Found) return(0); Found = false; N++; //////////////////////////// // for(u1x Vertical_N = 0; Vertical_N < Line_size; Vertical_N++) { if(Verticals_header[Vertical_N] == N) { //////////////////////////// // for(u1x Horizontal_N = 0; Horizontal_N < Line_size; Horizontal_N++) { if( (Cases_table[Horizontal_N * Line_size + Vertical_N] == 0) && (Horizontals_header[Horizontal_N] == 0 ) ) { Found = true; Horizontals_header[Horizontal_N] = N + 1; if( Horizontal_N == Line_size - 1 ) return(N+1); } }//for(u1x Horizontal_N = 0; Horizontal_N < Line_size; Horizontal_N++) }//if(Verticals_header[Vertical_N] == N) }//for(u1x Vertical_N = 0; Vertical_N < Line_size; Vertical_N++) if(!Found) return(0); N++; }//while(1) }//uint tCalculator::Make_wave() The result of the algorithm is shown in Fig. 24. No notes are entered in the table itself. In addition, for convenience, the Make_wave method returns a number starting from which the trace is being built, in this case 10.
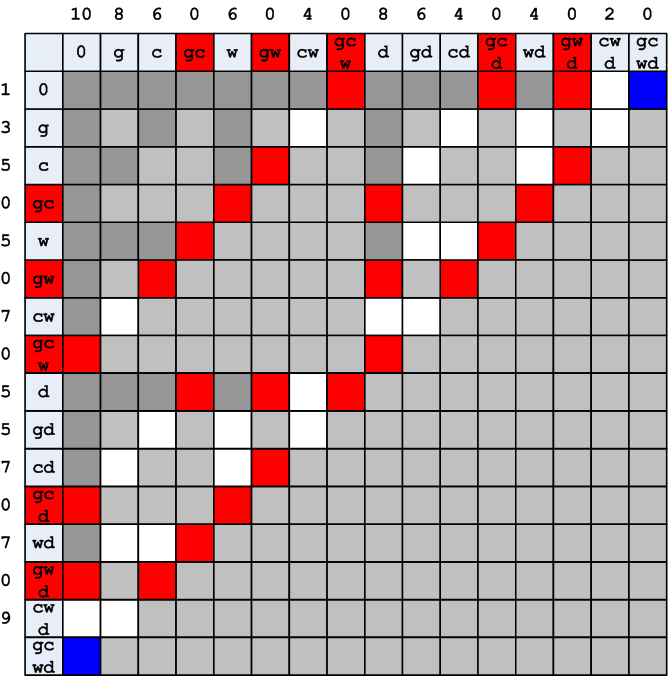
Figure 24. Built wave
After the wave is received, the line is under construction. The algorithm for constructing the route can be described by a state diagram.
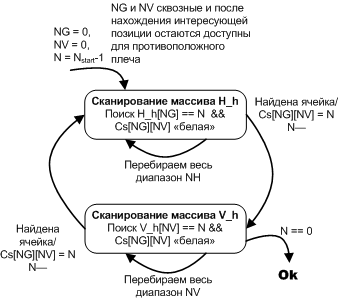
Figure 25. Algorithm for building a route
//////////////////////////////////////////////////////////////////////////////// //////////////////////////////////////////////////////////////////////////////// //////////////////////////////////////////////////////////////////////////////// //////////////////////////////////////////////////////////////////////////////// void tCalculator::Make_trace(u1x N) { u1x Horizontal_N = 0; u1x Vertical_N = 0; while(1) { ////////////////////////////// // Horizontals_header // N N--; for(Horizontal_N = 0; Horizontal_N < Line_size; Horizontal_N++) { if((Horizontals_header[Horizontal_N] == N)&&(Cases_table[Horizontal_N * Line_size + Vertical_N] == 0) ) { Cases_table[Horizontal_N * Line_size + Vertical_N] = N; break; } }//for(u1x Horizontal_N = 0; Horizontal_N < Line_size; Horizontal_N++) N--; if(!N) return; ////////////////////////////// // Verticals_header for(Vertical_N = 0; Vertical_N < Line_size; Vertical_N++) { if( ( Verticals_header[Vertical_N] == N) && (Cases_table[Horizontal_N * Line_size + Vertical_N] == 0) ) { Cases_table[Horizontal_N * Line_size + Vertical_N] = N; break; } }//for(Vertical_N = 0; Vertical_N < Line_size; Vertical_N++) }//while(1) }//void tCalculator::Make_trace() The project itself can be seen on bitbucket.
The Table_calculator module contains the description of the tCalculator class, which carries all the functionality.
Program
A few words about ways to further improve the described program. Consider the task:
You need to transport a goat, cabbage, a dog and two wolves in a boat from one bank to another. In the boat, only three places (one for the peasant). It is known that a wolf should not be left unattended with a goat and with a dog, a dog should not be left with a goat and, of course, the goat is not indifferent to cabbage. How to transport?
In this form, to find a solution to the problem with the help of the program described, one of the wolves will have to be designated by the letter w and the other by W, because the parser character ignores duplicate names. Accordingly, the prohibition rules must be set as wd, Wd.
It is relatively easy to make it possible to solve a problem for an arbitrary number of participants of the same name, listing them in the form 2w, 3g, 5c and setting the ban rules in a simple form wd for any wolf, or g5c (prohibition to leave the goat alone with 5 bags of cabbage, and it will eat at once and die), but the difference will be in the details, but the essence of the decision will remain the same. Therefore, I will not do it yet.
In conclusion, I will add that earlier I showed the process of practical decomposition as.
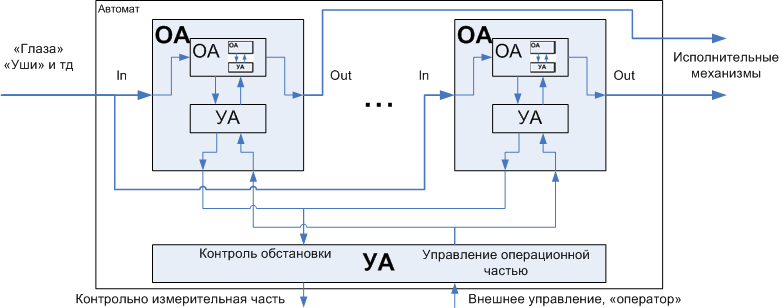
Figure 26. Multi-level decomposition of automata
The variant considered today is also an example of decomposition, but another kind is the conveyor of operating machines.
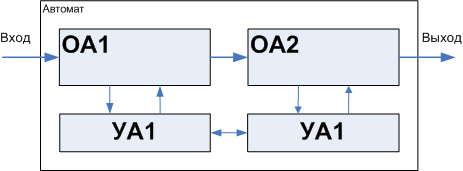
Figure 27. Machine conveyor decomposition
Since the choice of OA is so important, I will give more examples of solving problems by automaton design. That's all for today.
Source: https://habr.com/ru/post/343736/
All Articles