AlphaGo Zero completely on the fingers
Tomorrow, artificial intelligence will enslave the Earth and begin to use humans as ridiculous batteries that support the functioning of its systems, and today we stock up on popcorn and watch what it begins with.
On October 19, 2017, Deepmind team published an article in Nature , the brief essence of which is that their new model, AlphaGo Zero, not only defeats past versions of the network, but also does not require any human participation in the training process. Naturally, this statement produced the effect of a bombshell in the AI community, and everyone immediately became interested in how such a success was achieved.
Based on the materials in the public domain, Simon sim0nsays recorded a great stream:
')
And for those who find it easier to read two times than once, I’ll now try to explain all this with letters.
At once I want to note that the stream and the article were collected largely based on the discussions on closedcircles.com, hence the range of issues addressed, and the specific manner of the narration.
Let's go.
Go is an ancient (according to various estimates, it is from 2 to 5 thousand years old) board strategy game. There is a field, lined with perpendicular lines. There are two players, one in the bag has white stones, the other has black. Players take turns placing stones at the intersection of lines. Stones of the same color, surrounded in four directions by stones of a different color, are removed from the board:
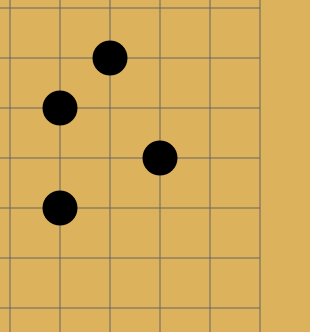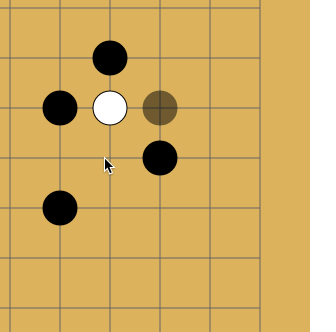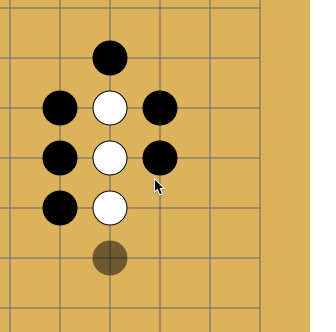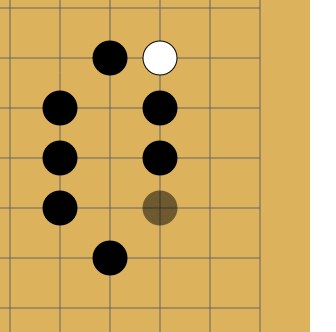
The one who "surrounds" the territory with the largest area by the end wins. There are still a few subtleties, but this is all basic - to a person who sees his first time in his life, it’s quite realistic to explain the rules in five minutes.
OK, let's try to compare several board games.
Let's start with the checkers. In checkers, the player has about 10 choices of what move to make. In 1994, the world drafts champion was beaten by a program written by researchers from the University of Alberta.
Next is chess. In chess, the player chooses an average of 20 valid moves and makes this choice about 50 times per game. In 1997, Deep Blue , created by the IBM team, beat the world chess champion Garry Kasparov.
Now go. Professionals play go on the field size 19x19, which gives 361 versions of where you can put the stone. Cutting frankly losing moves and points occupied by other stones, we still get a choice of more than 200 options, which are required to make an average of 50-70 times per game. The situation is complicated by the fact that the stones interact with each other, forming constructions, and as a result, a stone set on move 35 can benefit only at 115. But it may not. But more often it’s generally difficult to understand whether this move helped us or prevented. However, in 2016, the AlphaGo program beat the strongest (at least one of the strongest) player in the world, Lee Sedol, in a series of five games with a 4: 1 score.
Roughly speaking, yes. And in checkers, and in chess, and in go, the general principle on which the algorithms operate is the same. All these games fall into the category of games with complete information, which means that we can build a tree of all possible game states. Therefore, we simply build such a tree, and then just go along the branch that leads to victory. The subtlety is that for a tree, it turns out very large because of the strong branching factor and impressive depth, and it was not possible to build or bypass it in an adequate time. This problem was solved by the guys from DeepMind.
Here begins an interesting.
First, let's talk about how the go-to-AlphaGo algorithms worked. All of them showed not the most impressive results and successfully played at about the level of the average amateur, and all relied on the method called Monte Carlo Tree Search - MCTS. The idea of what (this is important to understand).
You have a tree of states - moves. From this particular situation, you walk along some of the branches of this tree until it ends. When a branch ends, you add a new node (node) to it, thereby incrementally completing this tree. And then you estimate the added node to determine whether it is worth walking along this branch or not, without revealing the tree itself.
A little more detailed, it works like this:
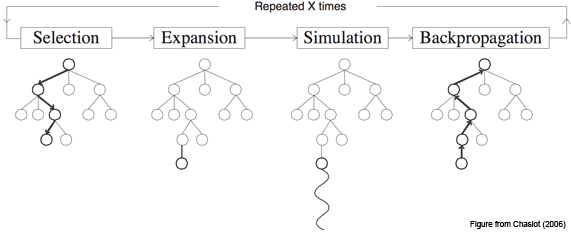
Step one, Selection: we have a position tree, and each time we make a move, choosing the best child for the current position.
Step two, Expansion: let's say we reached the end of the tree, but this is not the end of the game. Just create a new child node and go to it.
Step three, Simulation: well, a new node appeared, in fact, a game situation in which we found ourselves for the first time. Now we need to evaluate it, that is, to understand whether we are in a good situation or not. How to do it? In the basic concept - using the so-called rollout: just play a game (or many games) from the current position and see if we won or lost. The resulting result and consider the evaluation of the site.
Step Four, Backpropagation: go up the tree and increase or decrease the weights of all the parent nodes depending on whether the new node is good or bad. While it is important to understand the general principle, we will still have time to consider this stage in detail.
In each node, we store two values: the evaluation (value) of the current node and the number of times we ran through it. And we repeat the cycle of these four steps many, many times.
In the simplest version, we take a node that has the highest Upper Confidence Bounds (UCB):

Here, v is the value of our node, n is the number of times we have been in this node, N is the number of times we have been in the parent node, and C is just some coefficient.
In a not very simple version, you can complicate the formula to get more accurate results, or even use some other heuristic, such as a neural network. We will also talk about this approach.
If you look a little wider, we have the classic multi-armed bandit problem . The task is to find a node selection function that will provide the optimal balance between using the best available options and exploring new features.
Because with MCTS, the decision tree grows asymmetrically: more interesting nodes are visited more often, less interesting ones are less common, and it becomes possible to evaluate a single node without expanding the entire tree.

In general, AlphaGo relies on the same principles. The key difference is that when we add a new node in the second stage, in order to determine how good it is, we use a neural network instead of rollouts. How we do it.
(I’ll tell you in a few words about the previous version of AlphaGo, although in fact there are enough interesting nuances in it; who wants the details - just in the video in the beginning, there they are well explained, or in the corresponding post on Habré , there they are well- defined ).
First, we train two networks, each of which receives the state of the board as an input and says what move a person would make in this situation. Why two? Because one is slow, but it works well (57% of correct predictions, and each additional percentage gives a very solid bonus to the final result), and the second one has much less accuracy, but a quick one.
Both of these networks, slow and fast, we train on human moves - we go to the go server, we pick up lots of good level players, parsim and feed them for training.
Secondly, we take these two trained “in public” networks and start playing them with ourselves in order to pump them.

Like that.
Thirdly, we are training the value-network, which receives the current state of the board as input, and in response gives a number from -1 to 1 - the probability of winning, being in this position at some point in the game.
Thus, we have one slow and precise function that says where to go (from step 2), one fast function that does the same, though not so well (again from step 2), and the third function , which, looking at the board, says, you lose or win, if you find yourself in this situation (from step 3). Everything, now we play on MCTS and use the first one to see which nodes should be thrown from the current one, the second one in order to simulate rollout from the current position very quickly, and the third one to assess directly how good the node is. we shoved. For the total value, the values issued by the second and third networks are simply added together. As a result, we are very much cutting the branching factor, and we can not climb down the tree to assess the node (and if we climb, then quickly, quickly).
Yes, suddenly this is enough.
In October 2015, AlphaGo plays with three-time European champion Fan Hui and beats him 5-0. The event, on the one hand, is large, because for the first time a computer wins a professional in equal conditions, and on the other, not so much because in the world of European champion is about a water pump champion, and Fan Hui has only the second professional dan (out of nine possible). The version of AlphaGo, which played in this match, received the internal name AlphaGo Fan.
But in March 2016, the new AlphaGo version plays five games already with one of the best players in the world, Lee Sedol, and wins with a score of 4: 1. It's funny, but right after the games in the media, Lee Sedol became treated as the first top player who lost the AI, although time put everything in its place and for today Sedol remains (and probably will remain forever) the last person to beat the computer. But I'm running ahead. This version of AlphaGo in the future began to be designated AlphaGo Lee.

Nice try, Lee, but no.
After that, in the end of 2016 and the beginning of 2017, the next version of AlphaGo (AlphaGo Master) plays 60 matches online with players from the top positions of the world ranking and wins with a total score of 60: 0. In May, AlphaGo Master plays with Ke-Jie's top-1 world ranking and beats him 3-0. Actually, everything, the opposition of man and computer in go is complete.
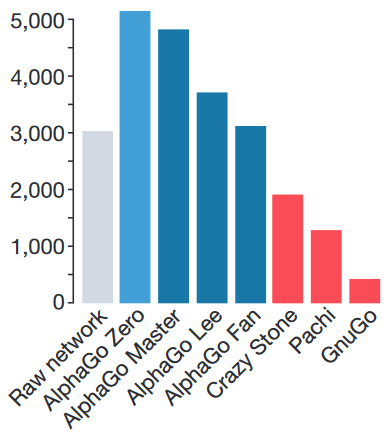
ELO rating. GnuGo, Pachi and CrazyStone are bots written without the use of neural networks.
In short - for beauty. The community had three relatively large claims against AlphaGo:
1) For starter training, people’s games are used. It turns out that without human intelligence, artificial intelligence does not work.
2) A lot of inherent features. I omitted this moment in my retelling, but in the video and in the post about AlphaGo Lee he gets enough attention, both of the networks used receive a significant number of features invented by people as input. By themselves, these features do not carry any new information and can be calculated based on the position of the stones on the board, but the networks cannot cope without them. For example, a network that determines the next move, in addition to the state itself, receives the following:
and so on - a total of 48 layers with information. A “fast” network, which predicts the probability of victory, altogether gives more than a hundred thousand parameters to the input. It turns out that the model learns not to play go per se, but to show results in some very well prepared environment in advance with a large number of properties, about which the person tells her again.
3) You need a healthy cluster to run it all.
And just a month ago, Deepmind introduced a new version of the algorithm, AlphaGo Zero, in which all these problems are eliminated - the model learns from scratch, playing exclusively with itself and using random neural network weights as starting ones; uses only the position of the stones on the board to make a decision; and much easier for the requirements of the gland. With a nice bonus, she beats AlphaGo Lee in opposition from a hundred games with a total score of 100: 0.
Two big things.
First, combine the two networks from past versions of AlphaGo into one. She gets the state of the board with a small number of features (I will talk about them a little later), drives all this stuff through its layers, and at the end its two outputs give two results: the policy output yields an array of 19x19, which shows how likely each of the moves from this position, and value gives one number - the probability of winning the game, again from this position.
Second, change the RL algorithm itself. If earlier MCTS was used only during the game, now it is used immediately during training. How it works.
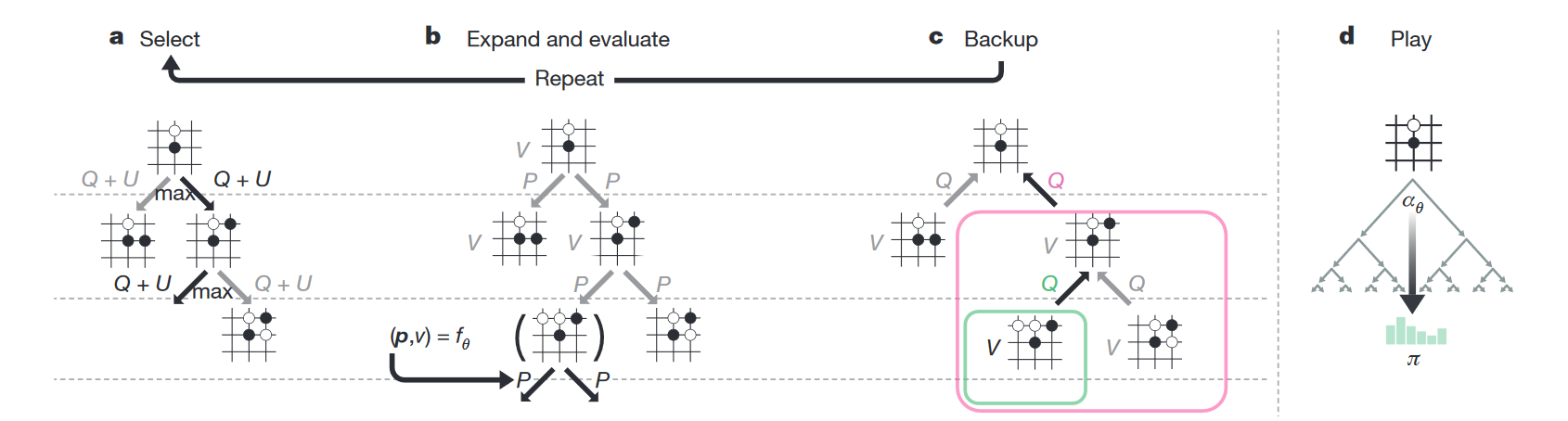
Each state tree node stores four values — N (how many times we walked along this node), V (value of this node), Q (average value of all the child nodes of this node) and P (the probability that we will choose this one). When the network plays with itself, during each turn it produces the following simulations:
Practice shows that such a simulation produces a much stronger prediction than the base neural network.
And then the move that the network really makes is selected in one of two ways:
- If this is a real game, go to where there is more N (it turned out that such a metric turns out to be the most reliable);
- If just training, choose a move from the distribution Pi ~ N ^ (1 / T) , where T is just some temperature to control the balance between research and efficiency.
The fact that both policy and value are predicted by one common network, makes it possible to run it all extremely effectively. We once found ourselves in some node, gave this node to our network, got some result V , all P was remembered as the initial weights on the child nodes, and that’s it, we don’t use the network more for this node, no matter how many times We went, and rollouts we do not run at all, considering that the predicted result is already quite accurate. Beauty.
The whole thing is being trained using this loss:
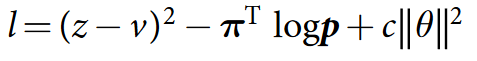
What is it, Barrymore?
The formula consists of three parts.
In the first part, we say that the network should be able to predict the result, that is, z (the result with which the game ended) should not differ from v (the value that it predicted).
In the second part we use our improved probabilities as labels for policy. It's like reward in supervised learning — we want to predict as accurately as possible the probabilities that we get by running over the tree; very similar to cross-entropy loss.
The third part, c at the end of the formula, is just a regularizer.
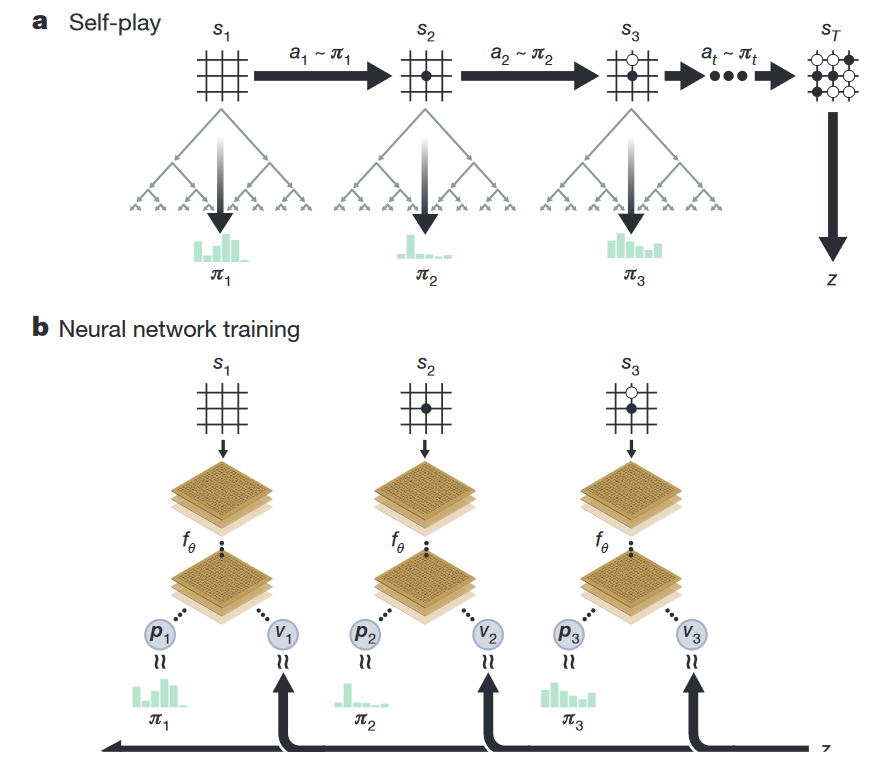
More globally, we have some “best” net with weights A. This network A plays with itself 25,000 times (using MCTS with its weights to evaluate new nodes), and for each move we save the state itself, the Pi distribution and what the game ended with (+1 for the victory and -1 for the defeat) . Then we prepare batches from 2048 random positions from the last 500,000 games, give 1000 such batches for training and we get some new network with weights B , after which network A plays 400 games with network B - while both networks use MCTS to select a turn, only when evaluating the new node A , obviously, uses its weights, and B - its own. If B wins in more than 55% of cases, it becomes the best network, if not - the champion remains the same. Repeat until ready.
Yeah, it was like that. So, the input is a field 19x19, each pixel of which has 17 channels, total we get 19x19x17. 17 layers are needed for the following.
The first one says if your stone is at this point or not (1 - stands, 0 - is missing), and the next seven - was it here in one of the previous seven moves.
The next eight layers are the same, but for the opponent’s stones.
The last, seventeenth, layer is clogged with units if you play black, and with zeros, if you play white. This is necessary, because in the final scoring White gets a small bonus for being the second.
That's all, in fact, the network really sees only the state of the board, but with information about what color of stones it plays, and the story for eight turns.
Convolutional layer, then 40 residual layers, at the end of the two exits - value head and policy head. I do not want to dwell on this in detail, for whom it is important — I will look at it myself, and the rest of the sections are hardly interesting. To summarize, in comparison with the version of the Lee, the network has become larger, they have added batch normalization and a residual connection has appeared. Innovations are very standard, very mainstream, there is no separate rocket science here.
And all this led to the following results.
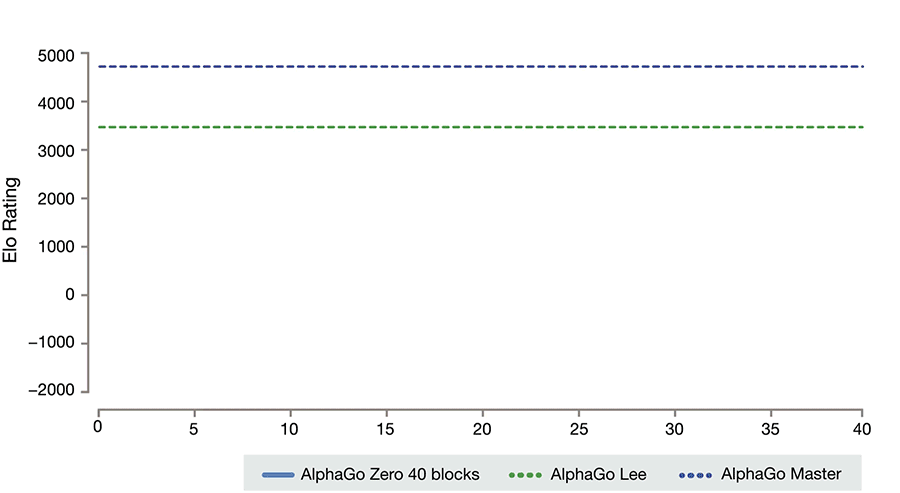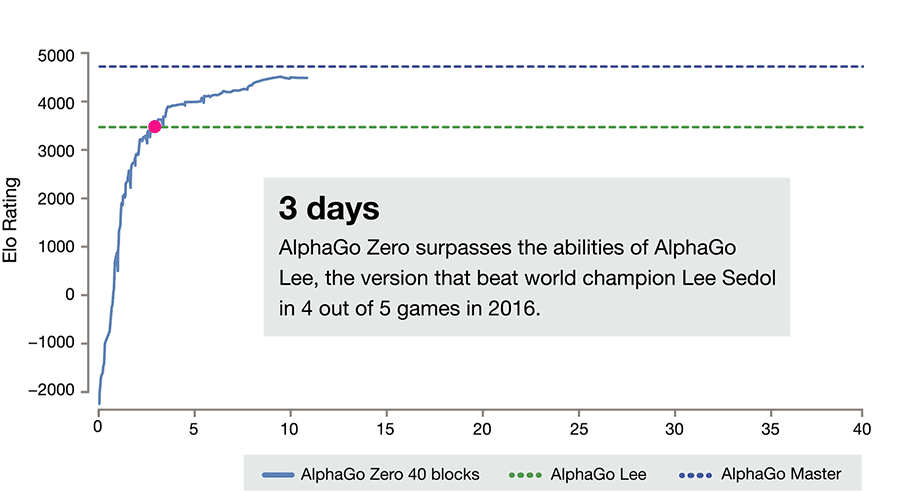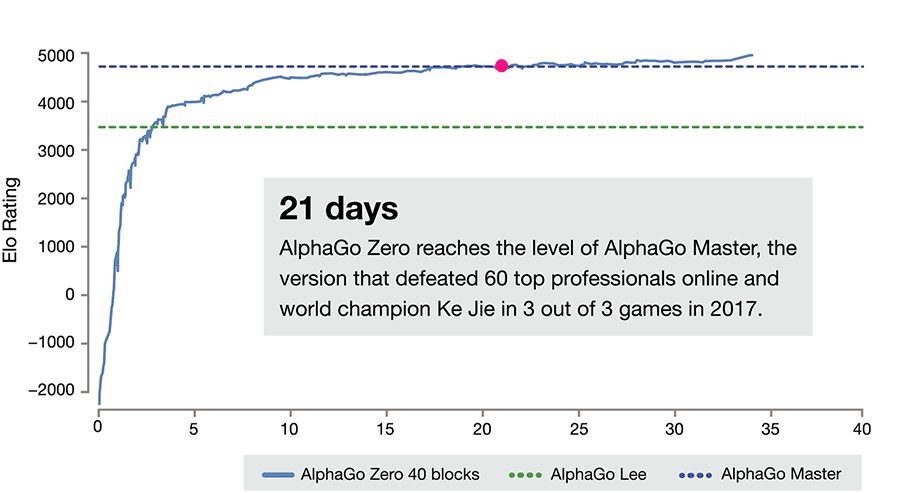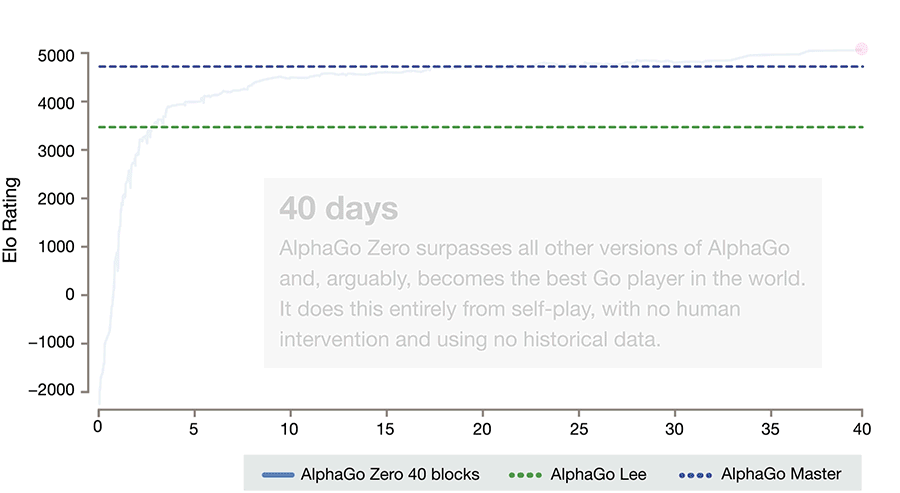
For three days AlphaGo Zero learns to beat the version of Lee, for 21 - the Master, and then goes into space. After 40 days of training, she beats the Lee version with a score of 100: 0 and the Master version with a score of 89:11. In this light, it is interesting to note that the Master and Zero have an identical training algorithm, an identical architecture, and all the differences lie in the features given to the input, and that Zero does not train on people’s games. And wins.
In go - it seems that yes, we are officially in persimmon. In general, no. Go has several features that are critical to current teaching methods:
In an environment strictly limited by this framework, we learned how to build systems whose efficiency is much higher than human. It is beyond the scope to go a little bit, and everything becomes much more difficult. More detail you can read in the post Andrej Karpathy .
In games - Starcraft and DotA. Active work is under way in both directions, but so far without breaks of a comparable scale. We wait.
First, watch the video at the beginning of this post, it is cool and covers many issues that I skipped.
Secondly, read the Seeds post about AlphaGo Lee .
Thirdly, come to the #data channel on closedcircles.com, we are actively discussing all this there.
Fourthly, everything that I have just told about AGZ is in one picture .
I will end this post with the last paragraph of the original paper:
Millions of games played over thousands of years, collectively distilled into patterns, proverbs and books. Zero Zero was able to make it out.
Just think about it.
Thanks to everyone who had the patience to scrape down to this place. Special thanks to users of sim0nsays for the content and comments and buriy for help in proofreading.
On October 19, 2017, Deepmind team published an article in Nature , the brief essence of which is that their new model, AlphaGo Zero, not only defeats past versions of the network, but also does not require any human participation in the training process. Naturally, this statement produced the effect of a bombshell in the AI community, and everyone immediately became interested in how such a success was achieved.
Based on the materials in the public domain, Simon sim0nsays recorded a great stream:
')
And for those who find it easier to read two times than once, I’ll now try to explain all this with letters.
At once I want to note that the stream and the article were collected largely based on the discussions on closedcircles.com, hence the range of issues addressed, and the specific manner of the narration.
Let's go.
What is go?
Go is an ancient (according to various estimates, it is from 2 to 5 thousand years old) board strategy game. There is a field, lined with perpendicular lines. There are two players, one in the bag has white stones, the other has black. Players take turns placing stones at the intersection of lines. Stones of the same color, surrounded in four directions by stones of a different color, are removed from the board:

The one who "surrounds" the territory with the largest area by the end wins. There are still a few subtleties, but this is all basic - to a person who sees his first time in his life, it’s quite realistic to explain the rules in five minutes.
And why is this considered difficult?
OK, let's try to compare several board games.
Let's start with the checkers. In checkers, the player has about 10 choices of what move to make. In 1994, the world drafts champion was beaten by a program written by researchers from the University of Alberta.
Next is chess. In chess, the player chooses an average of 20 valid moves and makes this choice about 50 times per game. In 1997, Deep Blue , created by the IBM team, beat the world chess champion Garry Kasparov.
Now go. Professionals play go on the field size 19x19, which gives 361 versions of where you can put the stone. Cutting frankly losing moves and points occupied by other stones, we still get a choice of more than 200 options, which are required to make an average of 50-70 times per game. The situation is complicated by the fact that the stones interact with each other, forming constructions, and as a result, a stone set on move 35 can benefit only at 115. But it may not. But more often it’s generally difficult to understand whether this move helped us or prevented. However, in 2016, the AlphaGo program beat the strongest (at least one of the strongest) player in the world, Lee Sedol, in a series of five games with a 4: 1 score.
Why did it take so much time to win a go? Are there so many options?
Roughly speaking, yes. And in checkers, and in chess, and in go, the general principle on which the algorithms operate is the same. All these games fall into the category of games with complete information, which means that we can build a tree of all possible game states. Therefore, we simply build such a tree, and then just go along the branch that leads to victory. The subtlety is that for a tree, it turns out very large because of the strong branching factor and impressive depth, and it was not possible to build or bypass it in an adequate time. This problem was solved by the guys from DeepMind.
And how did they win?
Here begins an interesting.
First, let's talk about how the go-to-AlphaGo algorithms worked. All of them showed not the most impressive results and successfully played at about the level of the average amateur, and all relied on the method called Monte Carlo Tree Search - MCTS. The idea of what (this is important to understand).
You have a tree of states - moves. From this particular situation, you walk along some of the branches of this tree until it ends. When a branch ends, you add a new node (node) to it, thereby incrementally completing this tree. And then you estimate the added node to determine whether it is worth walking along this branch or not, without revealing the tree itself.
A little more detailed, it works like this:

Step one, Selection: we have a position tree, and each time we make a move, choosing the best child for the current position.
Step two, Expansion: let's say we reached the end of the tree, but this is not the end of the game. Just create a new child node and go to it.
Step three, Simulation: well, a new node appeared, in fact, a game situation in which we found ourselves for the first time. Now we need to evaluate it, that is, to understand whether we are in a good situation or not. How to do it? In the basic concept - using the so-called rollout: just play a game (or many games) from the current position and see if we won or lost. The resulting result and consider the evaluation of the site.
Step Four, Backpropagation: go up the tree and increase or decrease the weights of all the parent nodes depending on whether the new node is good or bad. While it is important to understand the general principle, we will still have time to consider this stage in detail.
In each node, we store two values: the evaluation (value) of the current node and the number of times we ran through it. And we repeat the cycle of these four steps many, many times.
How do we select a child node in the first step?
In the simplest version, we take a node that has the highest Upper Confidence Bounds (UCB):

Here, v is the value of our node, n is the number of times we have been in this node, N is the number of times we have been in the parent node, and C is just some coefficient.
In a not very simple version, you can complicate the formula to get more accurate results, or even use some other heuristic, such as a neural network. We will also talk about this approach.
If you look a little wider, we have the classic multi-armed bandit problem . The task is to find a node selection function that will provide the optimal balance between using the best available options and exploring new features.
Why does this work?
Because with MCTS, the decision tree grows asymmetrically: more interesting nodes are visited more often, less interesting ones are less common, and it becomes possible to evaluate a single node without expanding the entire tree.

Does this have something to do with AlphaGo?
In general, AlphaGo relies on the same principles. The key difference is that when we add a new node in the second stage, in order to determine how good it is, we use a neural network instead of rollouts. How we do it.
(I’ll tell you in a few words about the previous version of AlphaGo, although in fact there are enough interesting nuances in it; who wants the details - just in the video in the beginning, there they are well explained, or in the corresponding post on Habré , there they are well- defined ).
First, we train two networks, each of which receives the state of the board as an input and says what move a person would make in this situation. Why two? Because one is slow, but it works well (57% of correct predictions, and each additional percentage gives a very solid bonus to the final result), and the second one has much less accuracy, but a quick one.
Both of these networks, slow and fast, we train on human moves - we go to the go server, we pick up lots of good level players, parsim and feed them for training.
Secondly, we take these two trained “in public” networks and start playing them with ourselves in order to pump them.

Like that.
Thirdly, we are training the value-network, which receives the current state of the board as input, and in response gives a number from -1 to 1 - the probability of winning, being in this position at some point in the game.
Thus, we have one slow and precise function that says where to go (from step 2), one fast function that does the same, though not so well (again from step 2), and the third function , which, looking at the board, says, you lose or win, if you find yourself in this situation (from step 3). Everything, now we play on MCTS and use the first one to see which nodes should be thrown from the current one, the second one in order to simulate rollout from the current position very quickly, and the third one to assess directly how good the node is. we shoved. For the total value, the values issued by the second and third networks are simply added together. As a result, we are very much cutting the branching factor, and we can not climb down the tree to assess the node (and if we climb, then quickly, quickly).
And it works much better than the option without neural networks?
Yes, suddenly this is enough.
In October 2015, AlphaGo plays with three-time European champion Fan Hui and beats him 5-0. The event, on the one hand, is large, because for the first time a computer wins a professional in equal conditions, and on the other, not so much because in the world of European champion is about a water pump champion, and Fan Hui has only the second professional dan (out of nine possible). The version of AlphaGo, which played in this match, received the internal name AlphaGo Fan.
But in March 2016, the new AlphaGo version plays five games already with one of the best players in the world, Lee Sedol, and wins with a score of 4: 1. It's funny, but right after the games in the media, Lee Sedol became treated as the first top player who lost the AI, although time put everything in its place and for today Sedol remains (and probably will remain forever) the last person to beat the computer. But I'm running ahead. This version of AlphaGo in the future began to be designated AlphaGo Lee.

Nice try, Lee, but no.
After that, in the end of 2016 and the beginning of 2017, the next version of AlphaGo (AlphaGo Master) plays 60 matches online with players from the top positions of the world ranking and wins with a total score of 60: 0. In May, AlphaGo Master plays with Ke-Jie's top-1 world ranking and beats him 3-0. Actually, everything, the opposition of man and computer in go is complete.

ELO rating. GnuGo, Pachi and CrazyStone are bots written without the use of neural networks.
But since they already beat everybody, why did they need another network?
In short - for beauty. The community had three relatively large claims against AlphaGo:
1) For starter training, people’s games are used. It turns out that without human intelligence, artificial intelligence does not work.
2) A lot of inherent features. I omitted this moment in my retelling, but in the video and in the post about AlphaGo Lee he gets enough attention, both of the networks used receive a significant number of features invented by people as input. By themselves, these features do not carry any new information and can be calculated based on the position of the stones on the board, but the networks cannot cope without them. For example, a network that determines the next move, in addition to the state itself, receives the following:
- how many moves a stone was put back;
- how many free points around this stone;
- how many of your stones will you sacrifice if you go to this point;
- whether this move is legal at all, that is, whether it is allowed by the rules of go;
- whether the stone put at this point will take part in the so-called “ladder” construction;
and so on - a total of 48 layers with information. A “fast” network, which predicts the probability of victory, altogether gives more than a hundred thousand parameters to the input. It turns out that the model learns not to play go per se, but to show results in some very well prepared environment in advance with a large number of properties, about which the person tells her again.
3) You need a healthy cluster to run it all.
And just a month ago, Deepmind introduced a new version of the algorithm, AlphaGo Zero, in which all these problems are eliminated - the model learns from scratch, playing exclusively with itself and using random neural network weights as starting ones; uses only the position of the stones on the board to make a decision; and much easier for the requirements of the gland. With a nice bonus, she beats AlphaGo Lee in opposition from a hundred games with a total score of 100: 0.
So, what did you have to do for this?
Two big things.
First, combine the two networks from past versions of AlphaGo into one. She gets the state of the board with a small number of features (I will talk about them a little later), drives all this stuff through its layers, and at the end its two outputs give two results: the policy output yields an array of 19x19, which shows how likely each of the moves from this position, and value gives one number - the probability of winning the game, again from this position.
Second, change the RL algorithm itself. If earlier MCTS was used only during the game, now it is used immediately during training. How it works.

Each state tree node stores four values — N (how many times we walked along this node), V (value of this node), Q (average value of all the child nodes of this node) and P (the probability that we will choose this one). When the network plays with itself, during each turn it produces the following simulations:
- Takes a tree whose root is the current node.
- It goes to that child node, where there is more Q + U ( U is an additive that stimulates the search for new ways; it is more at the beginning of the workout and less - in the future).
- In this simple way it reaches the end of the tree - the state when there are no child nodes, but the game is not over yet.
- Gives this state to the input of the neural network, in return receives v (value of the current node) and p (the probability of the next moves).
- Writes v to the node.
- Creates child nodes with P according to p and zero N , V and Q.
- Updates all nodes above the current one that were selected during the simulation as follows: N: = N + 1; V: = V + v; Q: = V / N.
- Repeats the cycle 1-7 1600 times.
Practice shows that such a simulation produces a much stronger prediction than the base neural network.
And then the move that the network really makes is selected in one of two ways:
- If this is a real game, go to where there is more N (it turned out that such a metric turns out to be the most reliable);
- If just training, choose a move from the distribution Pi ~ N ^ (1 / T) , where T is just some temperature to control the balance between research and efficiency.
The fact that both policy and value are predicted by one common network, makes it possible to run it all extremely effectively. We once found ourselves in some node, gave this node to our network, got some result V , all P was remembered as the initial weights on the child nodes, and that’s it, we don’t use the network more for this node, no matter how many times We went, and rollouts we do not run at all, considering that the predicted result is already quite accurate. Beauty.
How to train a network that must predict both policy and value?
The whole thing is being trained using this loss:
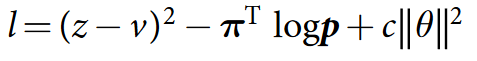
What is it, Barrymore?
The formula consists of three parts.
In the first part, we say that the network should be able to predict the result, that is, z (the result with which the game ended) should not differ from v (the value that it predicted).
In the second part we use our improved probabilities as labels for policy. It's like reward in supervised learning — we want to predict as accurately as possible the probabilities that we get by running over the tree; very similar to cross-entropy loss.
The third part, c at the end of the formula, is just a regularizer.

More globally, we have some “best” net with weights A. This network A plays with itself 25,000 times (using MCTS with its weights to evaluate new nodes), and for each move we save the state itself, the Pi distribution and what the game ended with (+1 for the victory and -1 for the defeat) . Then we prepare batches from 2048 random positions from the last 500,000 games, give 1000 such batches for training and we get some new network with weights B , after which network A plays 400 games with network B - while both networks use MCTS to select a turn, only when evaluating the new node A , obviously, uses its weights, and B - its own. If B wins in more than 55% of cases, it becomes the best network, if not - the champion remains the same. Repeat until ready.
And you also promised to tell you about the features that are served at the entrance.
Yeah, it was like that. So, the input is a field 19x19, each pixel of which has 17 channels, total we get 19x19x17. 17 layers are needed for the following.
The first one says if your stone is at this point or not (1 - stands, 0 - is missing), and the next seven - was it here in one of the previous seven moves.
Why do you need it
The fact is that repeats are forbidden in go - in some cases you cannot put a stone where it already stood. Like on a picture:
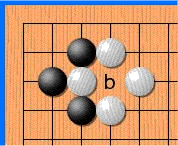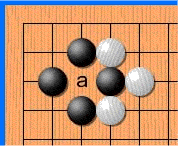
I do not know why, but Habr sometimes refuses to lose this gif. If that is what happened and you don’t see the animation, just click on it.
White makes a move to point a and takes the black stone. Black makes a move to point b and takes the white stone. Without a repetition ban, opponents could sit and play the a - b sequence indefinitely. In reality, White cannot immediately go back to position a and must choose another move (but after some other move, it is allowed to move to position a ). It is in order for the network to learn this rule that the story is transmitted to it. The second reason is that at AMA, the developers told me that when the network sees where activity has been lately, it learns better. In thought, this is something like attention .

I do not know why, but Habr sometimes refuses to lose this gif. If that is what happened and you don’t see the animation, just click on it.
White makes a move to point a and takes the black stone. Black makes a move to point b and takes the white stone. Without a repetition ban, opponents could sit and play the a - b sequence indefinitely. In reality, White cannot immediately go back to position a and must choose another move (but after some other move, it is allowed to move to position a ). It is in order for the network to learn this rule that the story is transmitted to it. The second reason is that at AMA, the developers told me that when the network sees where activity has been lately, it learns better. In thought, this is something like attention .
The next eight layers are the same, but for the opponent’s stones.
The last, seventeenth, layer is clogged with units if you play black, and with zeros, if you play white. This is necessary, because in the final scoring White gets a small bonus for being the second.
That's all, in fact, the network really sees only the state of the board, but with information about what color of stones it plays, and the story for eight turns.
And what about architecture?
Convolutional layer, then 40 residual layers, at the end of the two exits - value head and policy head. I do not want to dwell on this in detail, for whom it is important — I will look at it myself, and the rest of the sections are hardly interesting. To summarize, in comparison with the version of the Lee, the network has become larger, they have added batch normalization and a residual connection has appeared. Innovations are very standard, very mainstream, there is no separate rocket science here.
And all this to what?
And all this led to the following results.

For three days AlphaGo Zero learns to beat the version of Lee, for 21 - the Master, and then goes into space. After 40 days of training, she beats the Lee version with a score of 100: 0 and the Master version with a score of 89:11. In this light, it is interesting to note that the Master and Zero have an identical training algorithm, an identical architecture, and all the differences lie in the features given to the input, and that Zero does not train on people’s games. And wins.
That is all, the computer is smarter, humanity has no chance?
In go - it seems that yes, we are officially in persimmon. In general, no. Go has several features that are critical to current teaching methods:
- Always exactly defined environment for which there is an ideal and simple simulator; no accidents, no external interventions.
- Go - a game with complete information. A little bit like the previous point, but nevertheless - we know absolutely everything that happens.
In an environment strictly limited by this framework, we learned how to build systems whose efficiency is much higher than human. It is beyond the scope to go a little bit, and everything becomes much more difficult. More detail you can read in the post Andrej Karpathy .
What is the next bastion?
In games - Starcraft and DotA. Active work is under way in both directions, but so far without breaks of a comparable scale. We wait.
Wow! It seems a little clear. What else can be seen on the topic?
First, watch the video at the beginning of this post, it is cool and covers many issues that I skipped.
Secondly, read the Seeds post about AlphaGo Lee .
Thirdly, come to the #data channel on closedcircles.com, we are actively discussing all this there.
Fourthly, everything that I have just told about AGZ is in one picture .
And give finalechku.
I will end this post with the last paragraph of the original paper:
Millions of games played over thousands of years, collectively distilled into patterns, proverbs and books. Zero Zero was able to make it out.
Just think about it.
Thanks to everyone who had the patience to scrape down to this place. Special thanks to users of sim0nsays for the content and comments and buriy for help in proofreading.
Source: https://habr.com/ru/post/343590/
All Articles