Two geometric tasks that came across at the interview, and where they live
When a programmer goes to interviews, then sooner or later he is faced with mathematical puzzles. In this post I will look at two geometric problems and their solutions.
The first task is:
The second task is a bit more complicated, since the brute force has more options. So, the condition:
What was my surprise when after a month and a half, as I came across this task, I came across the book “Non-elementary tasks in elementary exposition” by A.M. Yaglom and I.M. Yaglom 1954 edition, which contains school olympiad tasks.

The problem of the plane in this collection is number one. So who is interested, can get acquainted with other tasks and solutions.
It's always like this: you go to school, you go to college, and the institute says “forget what you taught at school”, then you go to work and you hear “forget what you were taught at the institute”, then you go for some kind of interview, and you give a problem from school competitions =) Anyway, and knowledge is not superfluous.
Problem number 1
The first task is:
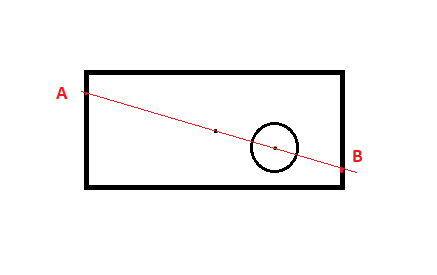
There is a rectangle, a circle is cut out in it, how many straight lines can be drawn,
which will divide into equal parts the resulting figure.
Decision:
Equal-sized figures are figures that have the same area. Remember that the circle is divided in half in the case of a straight line passing through its center. A rectangle is divided in half by lines passing through its center of intersection of the diagonals. Well, and the captain of evidence tells us that we will get equal parts of the figure if we draw a straight line through the centers of the rectangular figure and the cut out round part. Such a straight line is one if the centers of the rectangle and the circle do not coincide. In case of coincidence of the centers of the figures, the number of lines will be an infinite set. Made by

Problem number 2
The second task is a bit more complicated, since the brute force has more options. So, the condition:
How many planes can be drawn that are equidistant from four points in 3-dimensional space. These points do not lie in the same plane.
Decision:
If you read the condition carefully, you can pay attention to the fact that the four points do not lie on the same plane. This information reduces the number of possible locations of points that satisfy the condition of equidistance from the desired plane:
1) three points lie on one side of the plane in question, the fourth - on the other;
2) on each side of the plane lie two points.
')
Considering the first case, the possibility of the location of three points on one straight line is immediately excluded, since then a plane can be drawn through these three points and the fourth, and this contradicts the condition of the problem. So, the desired plane must be equidistant from three selected points (for example, A, B and C), which means it must be parallel to the plane ABC, drawn through these points. But the desired plane must also be equidistant from point D, so draw a plane parallel to the plane ABC through the middle of the perpendicular DP, lowered from point D to the plane ABC.

With respect to four points, we obtain four desired planes, equidistant from these points and such that on one side of them is located only one point, and on the other - the remaining three.
We proceed to the consideration of the second case.
Let points A and B lie on one side of the desired plane, and points C and D - on the other. Since the desired plane is equidistant from points A and B, it must be parallel to line AB. And since this plane is equidistant from points C and D, it must be parallel to the straight line CD. Points A, B, C and D do not lie in the same plane, then straight lines AB and CD are intersecting.

Draw through these intersecting straight parallel planes. In order for the desired plane to be equidistant from the points in question, it must be parallel to the constructed through intersecting straight planes and pass exactly midway between these planes. And for each such case under consideration, the desired plane will be unique.
Thus, there are three planes equidistant from the data of four points and such that on one side are two of the four points, and on the other side are the other two (AB and CD, AC and BD, AD and BC).
So, we get the total number of planes equidistant from these four points, equal to seven (four when considering the first case and three - the second case). The second problem is solved.
1) three points lie on one side of the plane in question, the fourth - on the other;
2) on each side of the plane lie two points.
')
Considering the first case, the possibility of the location of three points on one straight line is immediately excluded, since then a plane can be drawn through these three points and the fourth, and this contradicts the condition of the problem. So, the desired plane must be equidistant from three selected points (for example, A, B and C), which means it must be parallel to the plane ABC, drawn through these points. But the desired plane must also be equidistant from point D, so draw a plane parallel to the plane ABC through the middle of the perpendicular DP, lowered from point D to the plane ABC.

With respect to four points, we obtain four desired planes, equidistant from these points and such that on one side of them is located only one point, and on the other - the remaining three.
We proceed to the consideration of the second case.
Let points A and B lie on one side of the desired plane, and points C and D - on the other. Since the desired plane is equidistant from points A and B, it must be parallel to line AB. And since this plane is equidistant from points C and D, it must be parallel to the straight line CD. Points A, B, C and D do not lie in the same plane, then straight lines AB and CD are intersecting.
Definition of intersecting straight lines
Two straight lines are called crossing if they do not lie in the same plane.

Draw through these intersecting straight parallel planes. In order for the desired plane to be equidistant from the points in question, it must be parallel to the constructed through intersecting straight planes and pass exactly midway between these planes. And for each such case under consideration, the desired plane will be unique.
Theorem
Through each of the two crossed straight lines passes a plane parallel to the other straight line, and moreover only one.
Thus, there are three planes equidistant from the data of four points and such that on one side are two of the four points, and on the other side are the other two (AB and CD, AC and BD, AD and BC).
So, we get the total number of planes equidistant from these four points, equal to seven (four when considering the first case and three - the second case). The second problem is solved.
What was my surprise when after a month and a half, as I came across this task, I came across the book “Non-elementary tasks in elementary exposition” by A.M. Yaglom and I.M. Yaglom 1954 edition, which contains school olympiad tasks.

The problem of the plane in this collection is number one. So who is interested, can get acquainted with other tasks and solutions.
It's always like this: you go to school, you go to college, and the institute says “forget what you taught at school”, then you go to work and you hear “forget what you were taught at the institute”, then you go for some kind of interview, and you give a problem from school competitions =) Anyway, and knowledge is not superfluous.
Source: https://habr.com/ru/post/343526/
All Articles