Physically uncloneable functions: protecting electronics against illegal copying
Over the past 10 years, the number of fake goods in the world has increased by 2 times. This is a report from the Department of Homeland Security. Most of the counterfeit accounts for China (56%), Hong Kong (36%) and Singapore (2%).
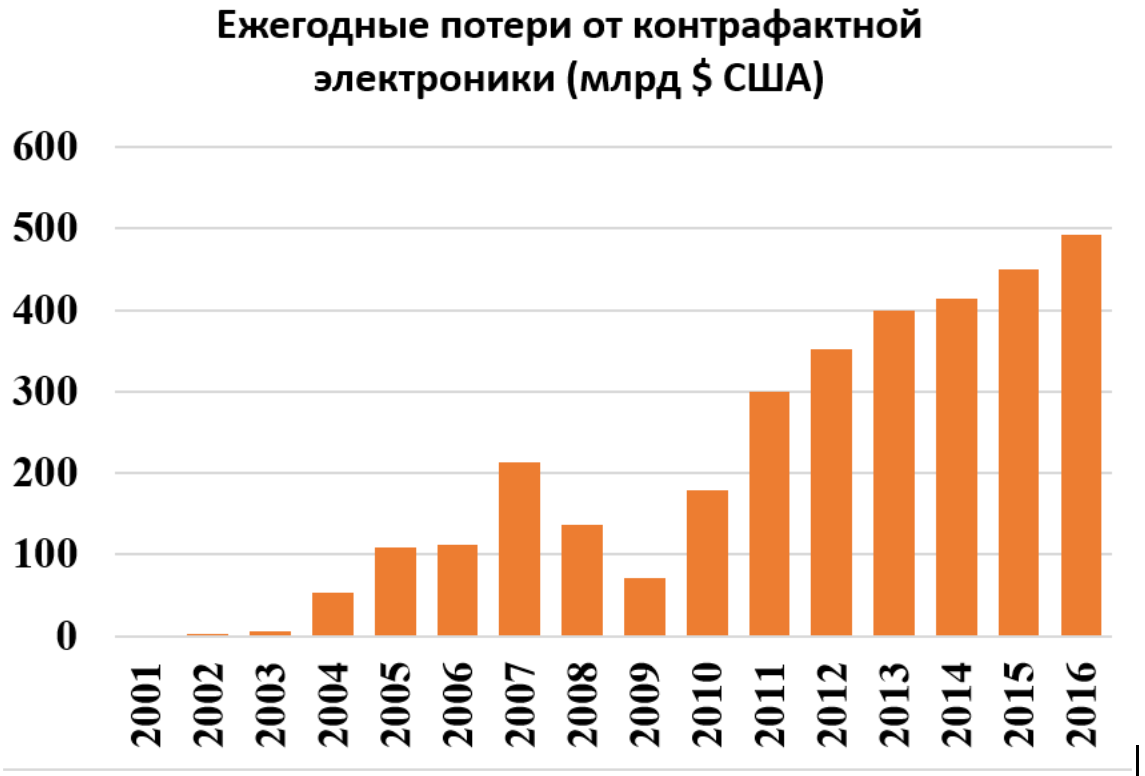
Manufacturers of original goods suffer serious losses, some of which occur in the electronics market. Many modern goods contain electronic components: clothing, shoes, watches, jewelry, cars. Last year, the direct losses from the illegal copying of consumer electronics and electronic components in the composition of other goods reached about 0.5 trillion US dollars.
')
This problem can be solved by various methods of protecting digital electronics from illegal copying, modification and reverse engineering: hardware encryption (AES, RSA, etc.), hashing (for example, SHA-256, MD-5), the introduction of digital watermarks and fingerprints in project description, lexical and functional obfuscation, formal verification and others.
In this article we will talk about one of the most economical methods of protection in terms of hardware costs - physically uncloned functions.
The disadvantage of most of the above methods are significant hardware costs and, as a result, high power consumption. With the emergence of the concept of the Internet of Things (Internet of Things, IoT), the requirements for the area occupied by a digital device on a chip of an integrated circuit, as well as for power consumption, become more stringent as the size of devices dramatically decreases from year to year.
One way to identify and authenticate digital devices is physically unclonable functions (FNF) (Physical Unclonable Functions, PUF), which are much more economical to implement than the above protection methods.
What is FNF (PUF)? Among the material objects around us it is difficult to find two absolutely identical objects. Even in mass production, each object is obtained uniquely due to errors and accidents. These features of each individual object can be registered and used as a unique identifier, a kind of “fingerprint”.
A good example is optical FNF (PUF) . Take the melted glass, add air bubbles to it, cool this mass and cut it into equal bars. The chance to get two absolutely identical bars is negligible because air bubbles inside will be distributed unevenly. We can capture these differences by sending a laser beam to the bar (request), and receiving a unique interference pattern of radiation beams after refraction (response). As a result, we get a physically non-clonable function that will determine the dependence of the response on the input request. Of course, this function is not analytic; neither the legal owner of the object, nor the intruder can recognize it in advance. You can only test the batch of products and create a table of input and output values, which will serve as a criterion for determining the authenticity of objects.
PUFs for protecting electronics are based on the use of manufacturing process variations (Variations) for the manufacture of integrated circuits: for example, accurate threshold voltages, signal propagation delays, component frequencies, etc. In the standard design process, digital device developers seek to reduce the impact of variations on the final product. In the case of FNP, on the contrary, this uncontrolled phenomenon is used to extract the randomness and uniqueness of a digital device.
Actually, the FNF is similar to hardware implementations of hash functions, with the only difference that the uniqueness of the output value of the FNF is based on the uniqueness of a particular integrated circuit, and not on a mathematical algorithm. The input argument of the FNF is called the request (Challenge, CH), and the output value is the answer (Response, R). Thus, for some integrated circuit ICk, the set of queries {CH 0 , ..., CH N-1 } will be uniquely mapped into the set of answers {R 0 , ..., R N-1 } using the FNF:
A set of request-response pairs (Challenge-Response Pairs, CRP) {(CH 0 , R0), ..., (CH N-1 , R N-1 )} uniquely characterizes the integrated circuit IC k and cannot be copied even if used absolutely identical project description (see diagram below).

Intercrystal and intracrystal uniqueness of integrated circuits (IC)
As shown in the diagram, when implementing an identical design description of the FNF on different ICs, the responses R i to the same query CH i will be unique (significantly different from each other) for each copy. This phenomenon is called intercrystalline uniqueness, i.e. ability to distinguish IP from each other using FNF. In the case of using identical realizations of FNF on a single chip to identify, for example, various components of intellectual property (Intellectual Property, IP), the phenomenon of intracrystal uniqueness is observed. Since the realizations of the FNP inside the crystal are different, at a minimum, in their mutual arrangement, the multi-crystal uniqueness is, as a rule, more pronounced than the intercrystalline.
Currently, there are many implementations of FNF based on:
As shown above, there is a wide variety of types of FNFs, which can be implemented both on digital devices and using other technologies (optical, magnetic, paper, etc.).
The first commercial implementation of FNF in 2008 was radio frequency identifiers manufactured by Verayo . Also currently, many FPGA manufacturers — for example, Xilinx and Altera (Intel) — use FNPs as the embedded non-cloning FPGA identifier. Since FNFs are used as cryptographic primitives (random number generators, unique identifiers, hardware hash functions), many manufacturers do not disclose the use of FNFs to keep the details of the implementation of their security protocols from intruders secret.
Let us give an example of the implementation of the FNF based on memory using the Xilinx Spartan 3E FPGA, which is part of the Digilent Nexys-2 rapid prototyping board. The memory element emulation was implemented as a bistable element, and the power on / off was modeled by reprogramming the FPGA with the same configuration file.
The figure below shows the identifiers of two identical FPGAs, obtained as a result of their programming with the same bit-file. The black color denotes “memory elements”, which retain the value of 0 as a result of 100 reprogramming, the white - retaining the value of 1. Those of them that change the value from start to start are shown in shades of gray. Accordingly, the more black in the “element” color, the more values of 0 were generated as a result of reprogramming.

64-bit identifiers of two identical FPGAs
As can be seen from the figure, “memory cards” differ significantly: the Hamming distance for 64-bit identifiers is about 20. Accordingly, the probability that the identifier will be the same on different FPGAs is quite small (less than 0.01). The above "memory cards" can be used in two ways: to identify the FPGA and as a source of randomness due to the presence of non-permanent elements.
Reliable identification will require the use of error correction codes (Error Correction Codes, ECC) to stabilize the observed “memory cards”. In this paper, the method of majority choice was used. To implement a random number generator, on the contrary, it requires “reproduction” of the randomness of those “memory elements” whose values are unstable. For this purpose, signature analysis was used as a lossy data compression scheme. Standard hashing algorithms (for example, SHA-256) can also be used if the hardware cost constraints are not so tight.
Despite the relative novelty of this concept, in 2017 the term FNF celebrates its 15th anniversary . During this time, the scientific community has already managed to study both the problems and possible applications of the FNF. One of the main problems, which is shown by the example of FNF based on memory, is the instability of some of the values, which, in turn, forces the developer to resort to error correction codes and more reliable FNF architectures. On the other hand, the presence of very high stability puts the PNF at risk of a cryptographic attack using machine learning methods, i.e. the construction is sufficiently accurate - more than 95% of the mathematical model of the PNF, which was initially (until 2010) considered impossible in the scientific community. Nevertheless, the use of FNF in modern commercial applications as a cryptographic primitive proves the promise of research in the field of searching for new FFF architectures, as well as improving the characteristics of existing implementations.
[!?] Questions and comments are welcome. They will be answered by the author of the article, Sergey Zalivako ( Siarhei Zalivaka ), Master of Technical Sciences, a graduate student at Nanyang Technological University (Nanyang Technological University), Singapore. Sergey specializes in the study of the stability of physically unclonable functions, their vulnerability to modeling using machine learning methods, as well as methods of active identification of integrated circuits (Integrated Circuit Active Metering).
Manufacturers of original goods suffer serious losses, some of which occur in the electronics market. Many modern goods contain electronic components: clothing, shoes, watches, jewelry, cars. Last year, the direct losses from the illegal copying of consumer electronics and electronic components in the composition of other goods reached about 0.5 trillion US dollars.

')
This problem can be solved by various methods of protecting digital electronics from illegal copying, modification and reverse engineering: hardware encryption (AES, RSA, etc.), hashing (for example, SHA-256, MD-5), the introduction of digital watermarks and fingerprints in project description, lexical and functional obfuscation, formal verification and others.
In this article we will talk about one of the most economical methods of protection in terms of hardware costs - physically uncloned functions.
The disadvantage of most of the above methods are significant hardware costs and, as a result, high power consumption. With the emergence of the concept of the Internet of Things (Internet of Things, IoT), the requirements for the area occupied by a digital device on a chip of an integrated circuit, as well as for power consumption, become more stringent as the size of devices dramatically decreases from year to year.
Physically uncloneable functions
One way to identify and authenticate digital devices is physically unclonable functions (FNF) (Physical Unclonable Functions, PUF), which are much more economical to implement than the above protection methods.
What is FNF (PUF)? Among the material objects around us it is difficult to find two absolutely identical objects. Even in mass production, each object is obtained uniquely due to errors and accidents. These features of each individual object can be registered and used as a unique identifier, a kind of “fingerprint”.
A good example is optical FNF (PUF) . Take the melted glass, add air bubbles to it, cool this mass and cut it into equal bars. The chance to get two absolutely identical bars is negligible because air bubbles inside will be distributed unevenly. We can capture these differences by sending a laser beam to the bar (request), and receiving a unique interference pattern of radiation beams after refraction (response). As a result, we get a physically non-clonable function that will determine the dependence of the response on the input request. Of course, this function is not analytic; neither the legal owner of the object, nor the intruder can recognize it in advance. You can only test the batch of products and create a table of input and output values, which will serve as a criterion for determining the authenticity of objects.
PUFs for protecting electronics are based on the use of manufacturing process variations (Variations) for the manufacture of integrated circuits: for example, accurate threshold voltages, signal propagation delays, component frequencies, etc. In the standard design process, digital device developers seek to reduce the impact of variations on the final product. In the case of FNP, on the contrary, this uncontrolled phenomenon is used to extract the randomness and uniqueness of a digital device.
Actually, the FNF is similar to hardware implementations of hash functions, with the only difference that the uniqueness of the output value of the FNF is based on the uniqueness of a particular integrated circuit, and not on a mathematical algorithm. The input argument of the FNF is called the request (Challenge, CH), and the output value is the answer (Response, R). Thus, for some integrated circuit ICk, the set of queries {CH 0 , ..., CH N-1 } will be uniquely mapped into the set of answers {R 0 , ..., R N-1 } using the FNF:
A set of request-response pairs (Challenge-Response Pairs, CRP) {(CH 0 , R0), ..., (CH N-1 , R N-1 )} uniquely characterizes the integrated circuit IC k and cannot be copied even if used absolutely identical project description (see diagram below).

Intercrystal and intracrystal uniqueness of integrated circuits (IC)
As shown in the diagram, when implementing an identical design description of the FNF on different ICs, the responses R i to the same query CH i will be unique (significantly different from each other) for each copy. This phenomenon is called intercrystalline uniqueness, i.e. ability to distinguish IP from each other using FNF. In the case of using identical realizations of FNF on a single chip to identify, for example, various components of intellectual property (Intellectual Property, IP), the phenomenon of intracrystal uniqueness is observed. Since the realizations of the FNP inside the crystal are different, at a minimum, in their mutual arrangement, the multi-crystal uniqueness is, as a rule, more pronounced than the intercrystalline.
Existing implementations of PNF and their application
Currently, there are many implementations of FNF based on:
- Signal propagation delays . Using the binary value of the request, the configuration of symmetrical paths is set, along which several copies of one signal are distributed. The response of the PNF is the result of comparing the propagation time delays.
- The frequency of the components . The basis of this PNF is a comparison of pairs of identical components whose frequency is unique. Requests are various pairs of indices of various components, and the answers are the result of comparing the frequency of their work.
- The state of the memory . As a result of power-up and / or resetting the state of static storage devices (SRAM), the value originally stored in each of the memory elements (0 or 1) is unique and random. The request in this FNF is power on / off, and the answer is the observed state of each of the memory elements, which uniquely characterizes the integrated circuit on which the FNF is implemented.
- Images on the photosensitive matrix . Each image created using a photosensitive matrix (Image Sensor) has a constant noise component that characterizes the uniqueness of the implemented matrix. The principle of operation of this FNF is similar to the FNF based on the comparison of frequencies with the only difference that the comparison is made by the values of the threshold voltage of each of the elements of the matrix.
- The threshold voltage of the transistor . This type of PNF can only be implemented analog, since in this case, the developer has access to the threshold voltage values. The basis for this FNF, like the FNF on the basis of frequencies, is the comparison of the characteristics of several transistors used in the integrated circuit.
- Current mirror . FNF of this class is based on the implementation of an array of current mirrors, the voltage values at the nodes of which uniquely characterize the integrated circuit. The query in this case are the numbers of the columns and rows of the elements, the voltage values in which you want to compare. The answer, respectively, is the result of comparing the voltage difference in a pair of nodes with a threshold value.
- The pressure of the user on the smartphone screen . In this implementation, the FNF request is a user action, which consists in holding a finger over a specific pattern (like a graphic key in smartphones). Based on the pressure values of the user on the smartphone screen, a unique response value is calculated, which characterizes the user and the smartphone and thus can be used for authentication.
- Paper structure . This implementation of the PNF is based on the uniqueness of the paper structure due to variations introduced into it during the production process. Accordingly, a certain paper medium can be used as a source of unique cryptographic keys.
As shown above, there is a wide variety of types of FNFs, which can be implemented both on digital devices and using other technologies (optical, magnetic, paper, etc.).
The first commercial implementation of FNF in 2008 was radio frequency identifiers manufactured by Verayo . Also currently, many FPGA manufacturers — for example, Xilinx and Altera (Intel) — use FNPs as the embedded non-cloning FPGA identifier. Since FNFs are used as cryptographic primitives (random number generators, unique identifiers, hardware hash functions), many manufacturers do not disclose the use of FNFs to keep the details of the implementation of their security protocols from intruders secret.
Memory Based FNF Example (SRAM)
Let us give an example of the implementation of the FNF based on memory using the Xilinx Spartan 3E FPGA, which is part of the Digilent Nexys-2 rapid prototyping board. The memory element emulation was implemented as a bistable element, and the power on / off was modeled by reprogramming the FPGA with the same configuration file.
The figure below shows the identifiers of two identical FPGAs, obtained as a result of their programming with the same bit-file. The black color denotes “memory elements”, which retain the value of 0 as a result of 100 reprogramming, the white - retaining the value of 1. Those of them that change the value from start to start are shown in shades of gray. Accordingly, the more black in the “element” color, the more values of 0 were generated as a result of reprogramming.

64-bit identifiers of two identical FPGAs
As can be seen from the figure, “memory cards” differ significantly: the Hamming distance for 64-bit identifiers is about 20. Accordingly, the probability that the identifier will be the same on different FPGAs is quite small (less than 0.01). The above "memory cards" can be used in two ways: to identify the FPGA and as a source of randomness due to the presence of non-permanent elements.
Reliable identification will require the use of error correction codes (Error Correction Codes, ECC) to stabilize the observed “memory cards”. In this paper, the method of majority choice was used. To implement a random number generator, on the contrary, it requires “reproduction” of the randomness of those “memory elements” whose values are unstable. For this purpose, signature analysis was used as a lossy data compression scheme. Standard hashing algorithms (for example, SHA-256) can also be used if the hardware cost constraints are not so tight.
Existing problems and prospects FNF
Despite the relative novelty of this concept, in 2017 the term FNF celebrates its 15th anniversary . During this time, the scientific community has already managed to study both the problems and possible applications of the FNF. One of the main problems, which is shown by the example of FNF based on memory, is the instability of some of the values, which, in turn, forces the developer to resort to error correction codes and more reliable FNF architectures. On the other hand, the presence of very high stability puts the PNF at risk of a cryptographic attack using machine learning methods, i.e. the construction is sufficiently accurate - more than 95% of the mathematical model of the PNF, which was initially (until 2010) considered impossible in the scientific community. Nevertheless, the use of FNF in modern commercial applications as a cryptographic primitive proves the promise of research in the field of searching for new FFF architectures, as well as improving the characteristics of existing implementations.
[!?] Questions and comments are welcome. They will be answered by the author of the article, Sergey Zalivako ( Siarhei Zalivaka ), Master of Technical Sciences, a graduate student at Nanyang Technological University (Nanyang Technological University), Singapore. Sergey specializes in the study of the stability of physically unclonable functions, their vulnerability to modeling using machine learning methods, as well as methods of active identification of integrated circuits (Integrated Circuit Active Metering).
Source: https://habr.com/ru/post/343386/
All Articles