Interpolation polynomial on arbitrary functions

Introduction

Greetings, dear readers! Today I propose to reflect on the following problem:

Given $$$n$ pairs of points on the plane $$$(x_1; y_1), ..., (x_n; y_n)$ . Everything $$$x_i$ are different. Need to find a polynomial $$$M (x)$ such that $$$M (x_i) = y_i$ where $$$i \ in \ {1, ..., n \}$

Translating into Russian, we have: Ivan thought $$$n$ points on the plane, and Mary, having this information, should come up with a function that (at least) will pass through all these points. In the framework of this article, our task is to help Mary in a roundabout way.
')
“Why in a roundabout way?” - you ask. The answer is traditional: this article is a continuation of a series of articles of amateurish nature about mathematics, the purpose of which is to popularize the mathematical world.

Process

To begin with, it is worth noting that some number of interpolation polynomials already exist, of course. These polynomials are designed to solve the desired problem. Among them, the Lagrange and Newton polynomials are especially known.

And it is also necessary to clarify what “arbitrary functions” are (the term comes from the title of the current article). By them is meant any unary function whose result is a bijective argument mapping .

Within the framework of this article, I propose to take the decimal logarithm for such a function. $$$\ lg$ and the following points:

$$

$$(0; 0) \\ (1; 1) \\ (2; 3) \\ (3; 0)$$

Representing them on a plane, you should get something like the following:


It is easy to notice that now the number of pairs of points is equal to $$$n = 4$ .

When solving this problem, a certain system of equations comes to mind, where the number of linearly independent rows is $$$n$ . What is this system of equations?

Let's try to write the function as a sum of decimal logarithms with coefficients of the variables (yes, so that the number of coefficients is equal to $$$n$ ):

$$

$$f (x) = a \ lg (x + 3) + b \ lg (x + 2) + c \ lg (x + 1) + d$$

Arguments at $$$\ lg$ different to avoid linear strings in the future (you can think of others). And also, given that the domain of function definition is at least $$$\ in [0; 3]$ (based on the points specified by the condition), we thus ensure the existence of a range of values ​​for the function $$$\ lg$ in this domain.

Since we know $$$n$ pairs of points, then we turn to them in order to build the following trivial system:

$$

$$\ begin {cases} \ displaystyle {f (0) = 0 \ Rightarrow a \ lg (3) + b \ lg (2) + c \ lg (1) + d = 0 \\ f (1) = 1 \ Rightarrow a \ lg (4) + b \ lg (3) + c \ lg (2) + d = 1 \\ f (2) = 3 \ Rightarrow a \ lg (5) + b \ lg (4) + c \ lg (3) + d = 3 \\ f (3) = 0 \ Rightarrow a \ lg (6) + b \ lg (5) + c \ lg (4) + d = 0} \ end {cases}$$

The triviality of the system is that we simply find such $$$a, b, c, d$ that will satisfy the entire set of conditions.

Actually solving this system regarding $$$a, b, c, d$ we get the following solution:

$$

$$\ begin {cases} \ displaystyle {a = \ frac {(5 \ lg ^ 2 (2) - 5 \ lg (2) \ lg (3) + \ lg (8/3) \ lg (5)) \ lg (10)} {3 \ lg ^ 3 (2) - \ lg (9/5) \ lg ^ 2 (2) + \ lg ^ 2 (3) \ lg (20) - \ lg (2) \ lg (5) \ lg (243/5)} \\ b = \ frac {\ lg (675/512) \ lg (2) \ lg (10)} {- 3 \ lg ^ 3 (2) + \ lg ( 9/5) \ lg ^ 2 (2) - \ lg ^ 2 (3) \ lg (20) + \ lg (2) \ lg (5) \ lg (243/5)} \\ c = \ frac { \ lg (10) (2 \ lg ^ 2 (2) + \ lg (2) (\ lg (3) - 7 \ lg (5)) + \ lg (5) \ lg (45))} {3 \ lg ^ 3 (2) - \ lg (9/5) \ lg ^ 2 (2) + \ lg ^ 2 (3) \ lg (20) - \ lg (2) \ lg (5) \ lg (243 / 5)} \\ d = \ frac {-9 \ lg ^ 3 (2) + \ lg ^ 2 (2) \ lg (25/9) + \ lg ^ 2 (3) \ lg (5) + \ lg (243/125) \ lg (2) \ lg (3)} {3 \ lg ^ 3 (2) - \ lg (9/5) \ lg ^ 2 (2) + \ lg ^ 2 (3) \ lg (20) - \ lg (2) \ lg (5) \ lg (243/5)}} \ end {cases}$$

This brings the task to a natural end, it remains only to write this into a single function:

$$

$$f (x) = \ frac {(5 \ lg ^ 2 (2) - 5 \ lg (2) \ lg (3) + \ lg (8/3) \ lg (5)) \ lg (10)} {3 \ lg ^ 3 (2) - \ lg (9/5) \ lg ^ 2 (2) + \ lg ^ 2 (3) \ lg (20) - \ lg (2) \ lg (5) \ lg (243/5)} \ lg (x + 3) \\ + \ frac {\ lg (675/512) \ lg (2) \ lg (10)} {- 3 \ lg ^ 3 (2) + \ lg (9/5) \ lg ^ 2 (2) - \ lg ^ 2 (3) \ lg (20) + \ lg (2) \ lg (5) \ lg (243/5)} \ lg (x + 2 ) \\ + \ frac {\ lg (10) (2 \ lg ^ 2 (2) + \ lg (2) (\ lg (3) - 7 \ lg (5)) + \ lg (5) \ lg ( 45))} {3 \ lg ^ 3 (2) - \ lg (9/5) \ lg ^ 2 (2) + \ lg ^ 2 (3) \ lg (20) - \ lg (2) \ lg ( 5) \ lg (243/5)} \ lg (x + 1) \\ + \ frac {-9 \ lg ^ 3 (2) + \ lg ^ 2 (2) \ lg (25/9) + \ lg ^ 2 (3) \ lg (5) + \ lg (243/125) \ lg (2) \ lg (3)} {3 \ lg ^ 3 (2) - \ lg (9/5) \ lg ^ 2 (2) + \ lg ^ 2 (3) \ lg (20) - \ lg (2) \ lg (5) \ lg (243/5)}$$

It will, of course, pass through a given set of points. A graph of the function will be as follows:


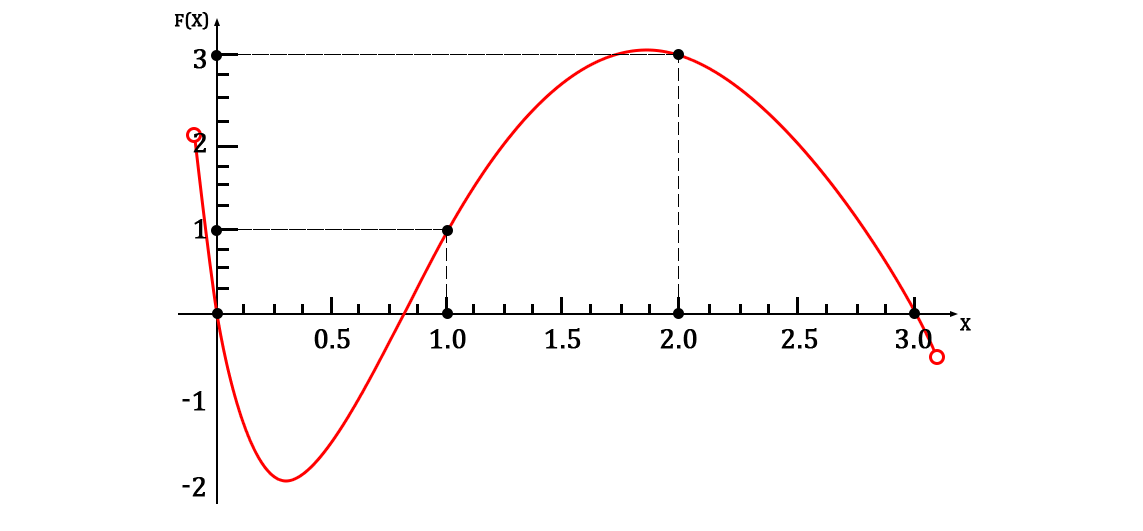
Also, for the sake of clarity, we can bring an approximated system of solutions:

$$

$$\ begin {cases} \ displaystyle {a \ approx-3428.6 \\ b \ approx3789.2 \\ c \ approx-790.20 \\ d \ approx495.22} \ end {cases}$$

Then the approximate form of the function will be as follows:

$$

$$f (x) = - 3428.6 \ lg (x + 3) +3789.2 \ lg (x + 2) -790.20 \ lg (x + 1) + $ 495.2$$

Of course, no one says that the resulting function will be minimal (the same Lagrange polynomial will give a shorter form). However, this method allows you to express a function through a set of arbitrary functions (although, referring to the restrictions specified above under the article).

Various examples

For dessert, we similarly construct a function in the radicals :

$$

$$f (x) = ax ^ 3 + bx ^ 2 + cx + d$$

We make the equation system for finding the coefficients:

$$

$$\ begin {cases} \ displaystyle {f (0) = 0 \ Rightarrow d = 0 \\ f (1) = 1 \ Rightarrow a + b + c + d = 1 \\ f (2) = 3 \ Rightarrow 8a + 4b + 2c + d = 3 \\ f (3) = 0 \ Rightarrow 27a + 9b + 3c + d = 0} \ end {cases}$$

Its solution is unique and looks like this:

$$

$$\ begin {cases} \ displaystyle {a = -1 \\ b = \ frac {7} {2} \\ c = - \ frac {3} {2} \\ d = 0} \ end {cases}$$

Then the finished function looks like this:

$$

$$f (x) = - x ^ 3 + \ frac {7} {2} x ^ 2- \ frac {3} {2} x$$

What is partly the Lagrange polynomial for a given set of points (since it implicitly implements the radical form of the algorithm from the article). The graph on the area of ​​given points looks like this:



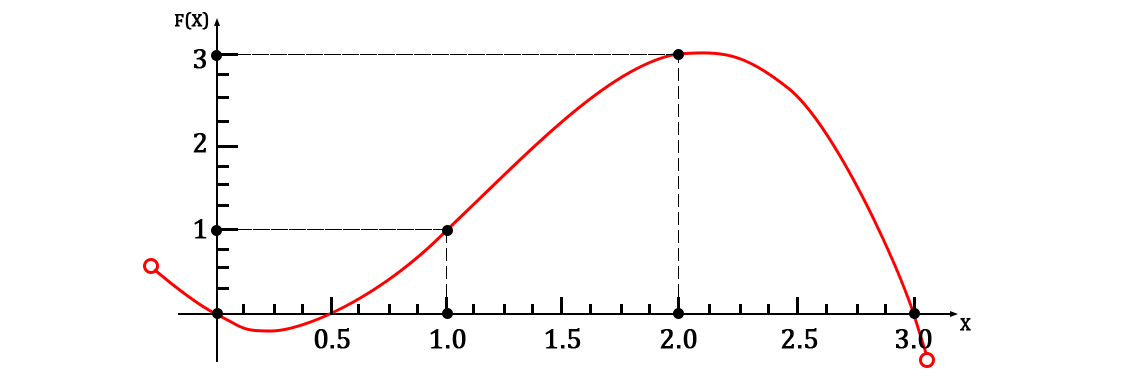
The most interesting thing in this story is that arbitrary functions for constructing a finite function can and should be combined. In other words, a function can be built immediately on radicals and logarithms, or maybe on something else (exponential functions, factorials, etc.). If only the resulting set of functions ensured linear independence of the rows when selecting coefficients. In general, for given $$$n$ pairs of points it looks like this:

$$

$$f (x) = a_1 * g_1 (x) + ... + a_n * g_n (x)$$

Where $$$a_1, .., a_n$ - coefficients to be found through the system of equations (SLAE), and $$$g_1, ..., g_n$ - Some functions that will provide linear independence in finding coefficients.

And then - according to the algorithm above, everything is completely the same. Not forgetting that $$$g_1, ..., g_n$ must be defined at the points specified by the condition.

For example, you can show a function consisting of completely different basic functions:

$$

$$f (x) = ax ^ 2 + b2 ^ x + cx + d$$

In order to satisfy a given set of points, the coefficients will then be the following (found strictly according to the algorithm from the article):

$$

$$\ begin {cases} \ displaystyle {a = \ frac {7} {2} \\ b = -6 \\ c = \ frac {7} {2} \\ d = 6} \ end {cases}$$

And the function itself will be:

$$

$$f (x) = \ frac {7} {2} x ^ 2-6 * 2 ^ x + \ frac {7} {2} x + 6$$

The graph will look almost the same as the previous one (on the area of ​​specified points).
If you want a more “smooth” graph, then you can look towards the factorial form, for example:

$$

$$f (x) = a (x + 2)! + b (x + 1)! + cx! + d$$

Find the coefficients:

$$$$ display $$ \ begin {cases} \ displaystyle {2a + b + c + d = 0 \\ 6a + 2b + c + d = 1 \\ 24a + 6b + 2c + d = 3 \\ 120a + 24b + 6c + d = 0} \ end {cases} \ Rightarrow \ begin {cases} \ displaystyle {a = -13/16 \\ b = 17/4 \\ c = -3/8 \\ d = -9 / 4 } \ end {cases} $$ display $$

Substitute these into the finished function:

$$

$$f (x) = - \ frac {13} {16} (x + 2)! + \ frac {17} {4} (x + 1)! - \ frac {3} {8} x! - \ frac {9} {4}$$

And also admire a very good schedule:

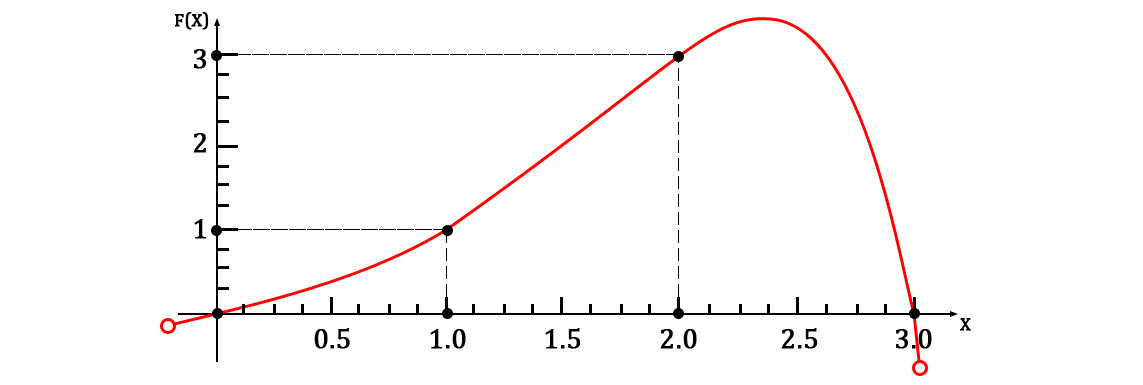
Why do you need it?

Yes, at least in order to imagine a bunch of ropes tied with plastic straps :)

( * Here we just put all the graphics on each other )

On this, in the framework of the current article, I recommend playing on your own.

All the best,
Peter was with you.