On fractals, martingales and random integrals. Part one

In my opinion, stochastic calculus is one of those magnificent sections of higher mathematics (along with topology and complex analysis), where formulas are found with poetry; this is the place where they acquire beauty, the place where the scope for artistic creativity begins. Many of those who read the article Wiener Chaos or Another way to flip a coin , even if they understood little, could still appreciate the magnificence of this theory. Today we will continue our mathematical journey, we will plunge into the world of random processes, non-trivial integration, financial mathematics and even touch on functional programming a little. I warn you, keep your brains ready, as we have a serious conversation.


By the way, if you are interested in reading in a separate article, it suddenly turned out that

$$

$$dX ^ 2 \ neq 2X \ cdot dX,$$

I added a poll below where you can leave your vote.

Hidden threat of fractals

Imagine some simple function. $$$f (t)$ at some interval $$$[t, t + \ Delta t]$ . Submitted? In standard mathematical analysis, we are accustomed to the fact that if the dimensions of this interval are reduced long enough, then the function given to us starts to behave rather smoothly, and we can bring it closer to a straight line, in a pinch, with a parabola. All thanks to the theorem on the decomposition of the function formulated by the English scientist Brooke Taylor in 1715:

$$

$$f (t + \ Delta t) = f (t) + f '(t) \ cdot \ Delta t + \ frac {1} {2} f' '(t) \ cdot (\ Delta t) ^ 2 + \ cdots$$

This theorem is skillfully handled by modern mathematics engineers, approximating everything for their numerical calculations. But on fractals, such a scheme fails.

By the time Benoit Mandelbrot invented the very concept of "fractals", they had been preventing many world scientists from sleeping for a hundred years. One of the first to whom fractals tarnished his reputation was Andre-Marie Ampère. In 1806, the scientist put forward a rather convincing "proof" of the fact that any function can be divided into intervals of continuous functions, and these, in turn, due to continuity, must have a derivative. And many of his contemporary mathematicians agreed with him. In general, Ampere cannot be blamed for this, seemingly rather gross error. Mathematicians of the beginning of the 19th century had a rather vague definition of such nowadays as basic concepts of mathematical analysis as continuity and differentiability, and, as a result, they could be greatly mistaken in their evidence. Even such eminent scientists as Gauss, Fourier, Cauchy, Legendre, Galois, not to mention much less well-known mathematicians of those times, were no exception.
')
Nevertheless, in 1872, Karl Weierstrass refuted the hypothesis of the existence of derivatives of continuous functions, presenting on display the world's first fractal monster, everywhere continuous and never differentiable.

Here, for example, how this function is defined:

$$

$$f (t) = \ sum_ {n = 0} ^ \ infty \ frac {\ sin (2 ^ n t)} {2 ^ n}$$

The Brownian movement has the same property (by the way, for some reason, not Br, but Unov, the surname is British, though). Brownian motion is a continuous, random process. $$$B (t)$ such that all its increments are independent and have a normal distribution:

$$

$$B (T) -B (t) \ sim \ mathcal {N} (0, T- t), \ quad t <T.$$

The trajectories of the Brownian motion are fractal functions, they are continuous everywhere and non-smooth. But if the Weierstrass function was just a counterexample, let it be one of the brightest in the entire history of mathematical analysis, the Brownian movement promised to become the foundation of the stochastic theory, and it was necessary to somehow learn to work with it.

Infinite variation of the Brownian motion

Let's imagine the function again $$$f (t)$ on the interval $$$t \ in [0, T]$ and divide this interval into a set of $$$n$ non-intersecting subintervals:

$$

$$\ Pi = \ {0 = t_0 <t_1 <\ dots <t_n = T \}.$$

We don't care how the points are distributed. $$$t_0, \ dots, t_n$ , breaking this interval, the size of the maximum step is much more interesting: $$$\ | \ Pi \ | = \ max_ {i = 1, \ dots, n} (t_ {i} -t_ {i-1}).$ We will call the value

$$

$$V _ {[0, T]} ^ f = \ lim _ {\ | \ Pi \ | \ rightarrow 0} \ sum_ {i = 1} ^ n | f (t_ {i}) - f (t_ {i-1}) |$$

variation of the (first kind) function $$$f (t)$ (also referred to as general variation). If a $$$V _ {[0, T]} ^ f <\ infty$ then we say that $$$f (t)$ has a finite variation. For example, a variation of a rather “smooth” function.

will be the ultimate. In which case are we not so sure? Well, for example, the function will not have a finite variation.

$$

$$f (t) = 1_ \ mathbb {Q} (t),$$

returning $$$1$ for all rational $$$t$ and $$$0$ for all irrational. Similar logic can be extended to random functions. Let him $$$X (t)$ - This is a random process. The variation for it is set in the same way:

$$

$$V _ {[0, T]} ^ X (\ omega) = \ lim _ {\ | \ Pi \ | \ rightarrow 0} \ sum_ {i = 1} ^ n | X (t_ {i}) - X (t_ {i-1}) | (\ omega).$$

The only difference is that the variation will also become random (the parameter $$$\ omega$ for convenience, you can omit it, but it seems to hint here that the variation from the random process is a mapping from the space of random events $$$\ Omega$ at $$$\ mathbb {R}$ ).

This is how a fairly simple implementation of a variation on Haskell will look like:

-- | 'totalVariation' calculates total variation of the sample process X(t) totalVariation :: [Double] -- process trajectory X(t) -> Double -- V(X(t)) totalVariation x@(_:tx) = sum $ zipWith (\x xm1 -> abs $ x - xm1) tx x 

Where do random processes occur in the real world? One of the most famous examples today is financial markets, namely the movement of prices for currency, stocks, options, and various securities. Let him $$$X (t)$ - this is Apple stock value. At some point you decided to buy $$$f (t_0)$ stock by price $$$X (t_0)$ and after a certain period of time the price changed and became equal $$$X (t_1)$ . As a result, you have $$$f (t_0) \ cdot \ Delta X (t_1)$ net profit / loss, where $$$\ Delta X (t_i) = X (t_i) -X (t_ {i-1})$ . You have decided to buy / sell part of the shares and now you are holding $$$f (t_1)$ valuable papers. After some time, your income / losses amount to $$$f (t_0) \ cdot \ Delta X (t_1) + f (t_1) \ cdot \ Delta X (t_2)$ , etc. In the end, you will earn / lose

$$

$$I (T) = \ sum_ {i = 1} ^ n f (t_ {i-1}) \ cdot \ Delta X (t_i).$$

It's pretty simple, but here's the catch: the process of changing the price of a share can move very quickly, just like our process of buying / selling it (the so-called High Frequency Trading). I would like to extend these calculations to continuous processes and present our revenues in the form of an integral like $$$I (T) = \ int_0 ^ T f (t) dX (t).$ The problem is that we do not yet know how to take integrals over random processes and their trajectories. But we remember by what principle the standard Lebesgue integral (-Stilties) is defined. Usually, you first need to set the appropriate measure. Take a non-decreasing process $$$X (t)$ , for simplicity, starting from scratch: $$$X (0) = 0$ and nonnegative measure corresponding to its increments

$$

$$\ mu_X (a, b]: = X (b) -X (a).$$

If the function $$$f (t)$ limited and measurable (recall the functional analysis) we can determine the integral for it on the interval $$$[0, T]$ as

$$

$$\ int_0 ^ T f (t) dX (t) = \ int _ {[0, T]} f (t) \ mu_X (dt).$$

For the general case, if the trajectories of a random process do not have monotony, we can divide it into two non-decreasing processes: $$$X (t) = X ^ + (t) -X ^ - (t),$ and then we define the Lebesgue integral as

$$

$$\ int_0 ^ T f (t) dX (t) = \ int _ {[0, T]} f (t) \ mu_ {X ^ +} (dt) - \ int _ {[0, T]} f (t ) \ mu_ {X ^ -} (dt).$$

A necessary condition for the existence of such an integral is the existence $$$V _ {[0, T]} ^ X$ . Indeed, if our process consists of the difference of two non-decreasing processes, then it has a finite variation (in the second line we used the triangle inequality):

$$

$$\ begin {aligned} V _ {[0, T]} ^ X & = \ lim _ {\ | \ Pi \ | \ rightarrow 0} \ sum_ {i = 1} ^ n | X (t_ {i}) - X (t_ {i-1}) | \\ & \ leq \ lim _ {\ | \ Pi \ | \ rightarrow 0} \ Big (\ sum_ {i = 1} ^ n | X ^ + (t_ {i}) - X ^ + (t_ {i-1}) | + \ sum_ {i = 1} ^ n | X ^ - (t_ {i}) - X ^ - (t_ {i-1}) | \ Big) \\ & = X ^ + (T) + X ^ - (T) <\ infty. \ end {aligned}$$

By the way, this condition also works in the opposite direction: if we have a process $$$X (t)$ with finite variation then we can define $$$X ^ + (t) = \ frac {1} {2} (| X (t) | + X (t))$ and $$$X ^ - (t) = \ frac {1} {2} (| X (t) | -X (t))$ . Monotony and equality $$$X = X ^ + - X ^ -$ easy to prove.

Now we can easily integrate something. Take the trajectory of some continuous random process and call it $$$g (t)$ . Using the Lagrange mean theorem, we can show that for a continuous function $$$g (t)$ the variation will be equal $$$V _ {[0, T]} ^ g = \ int_0 ^ T | g '(t) | dt$ . If this integral exists, then under the above mentioned conditions of boundedness and measurability $$$f (t)$ we can count

$$

$$\ int_0 ^ Tf (t) dg (t) = \ int_0 ^ Tf (t) g '(t) dt.$$

It really is easy. What about fractals, trajectories like the Weierstrass monster? After all, for them there is no $$$g '(t)$ .



So the question is: is it possible to take the integral in the sense of Lebesgue from the Brownian motion? We calculate the variation, and if it is finite, then we should not have any problems. Let's go from the side of the so-called quadratic variation :

$$

$$[B] (T) = \ lim _ {\ | \ Pi \ | | \ rightarrow 0} \ sum_ {i = 1} ^ n \ big (B (t_ {i + 1}) - B (t_i) \ big) ^ 2$$

What do you think this limit is? We will consider a random variable $$$[B] (t) -t$ and show that its variance equals zero:

$$

$$\ begin {aligned} \ sum_ {i = 1} ^ n \ big (B (t_ {i + 1}) - B (t_i) \ big) ^ 2-T & = \ sum_ {i = 1} ^ n \ Big (\ big (B (t_ {i + 1}) - B (t_i) \ big) ^ 2- (t_ {i + 1} -t_i) \ Big) \\ & = \ sum_ {i = 1} ^ n (Z_i ^ 2-1) (t_ {i + 1} -t_i), \ end {aligned}$$

Where

$$

$$Z_i = \ frac {B (t_ {i + 1}) - B (t_i)} {\ sqrt {t_ {i + 1} - t_i}} \ sim \ mathcal {N} (0,1)$$

standard normally distributed quantity. In particular, since all $$$Z_i ^ 2$ are independent and have a chi-square distribution with degree 1, it’s easy to calculate that

$$

$$\ mathbb {E} [(Z_i ^ 2-1) ^ 2] = \ operatorname {Var} (Z_i ^ 2) = 2.$$

Consequently,

$$

$$\ begin {aligned} \ mathbb {E} \ bigg [\ Big (\ sum_ {i = 1} ^ n \ big (B (t_ {i + 1})) - B (t_i) \ big) ^ 2 -T \ Big) ^ 2 \ bigg] & = \ sum_ {i = 1} ^ n \ mathbb {E} [(Z_i ^ 2-1) ^ 2 (t_ {i + 1} -t_i) ^ 2] \\ & = 2 \ sum_ {i = 1} ^ n (t_ {i + 1} -t_i) ^ 2 \\ & \ leq \ | \ Pi \ | \ cdot 2 \ sum_ {i = 1} ^ n (t_ {i + 1} -t_i) \ rightarrow 0. \ end {aligned}$$

In other words,

$$

$$[B] (T) = T.$$

Remember this formula! It is the foundation of stochastic analysis, a kind of local analogue of the central limit theorem, and all other theorems explicitly and implicitly revolve around it.

Notice that $$$[B] (T) = \ operatorname {Var} (B (T))$ however, the methods for calculating these two values ​​are completely different. The dispersion of the Brownian motion is considered to be the averaging of all its trajectories, given their probabilities. The quadratic variation is taken from a single random trajectory along which the movement took place, and the probabilities do not play a role here. While the variance can only be calculated theoretically, since it requires averaging of all implementations, the quadratic implementation can be calculated explicitly (with a sufficient data sampling value). The above formula is interesting in particular because, by definition, the quadratic variation, like the variation of the first kind $$$V _ {[0, T]} ^ X$ is a random variable. However, the feature of the Brownian movement is that its quadratic variation degenerates and takes only one single value corresponding to the length of the interval, regardless of the trajectory along which the movement took place.

We write a code that considers the quadratic variation of the implementation of a random process $$$X (t)$ :

 -- | 'quadraticVariation' calculates quadratic variation of the sample process X(t) quadraticVariation :: [Double] -- process trajectory X(t) -> Double -- [X(t)] quadraticVariation x@(_:tx) = sum $ zipWith (\x xm1 -> (x - xm1) ^ 2) tx x 

So now we are ready to return to calculating the variation of interest. $$$V _ {[0, T]} ^ B$ . We found out that

$$

$$\ lim _ {\ | \ Pi \ | \ rightarrow 0} \ sum_ {i = 1} ^ n (B (t_ {i + 1}) - B (t_i)) ^ 2 = T.$$

That is, it is non-zero, but not infinite. On the other hand, it is bounded above by the maximum pitch of the broken $$$B (t)$ :

$$

$$\ begin {aligned} \ sum_ {i = 1} ^ n (B (t_ {i + 1}) - B (t_i)) ^ 2 \ leq \ max \ big \ {| B (t_ {i + 1} ) - B (t_i) | \ big | (t_ {i}, t_ {i + 1}) \ subset \ Pi \ big \} \ cdot \ sum_ {i = 1} ^ n | B (t_ {i + 1}) - B (t_i) | . \ end {aligned}$$

We know that the Brownian motion is a continuous process, which means

$$

$$\ max \ big \ {| B (t_ {i + 1}) - B (t_i) | \ big | (t_ {i}, t_ {i + 1}) \ subset \ Pi \ big \} \ rightarrow 0.$$

But, $$$\ sum_ {i = 1} ^ n | B (t_ {i + 1}) - B (t_i) | \ rightarrow V _ {[0, T]} ^ B.$ And as a consequence,

$$

$$V _ {[0, T]} ^ B = \ infty.$$

Y-yes ...

Ito integral or New Hope

In 1827, the English botanist Robert Brown, observing pollen grains in water through a microscope, noticed that the particles inside their cavity move in a certain way; however, he was then unable to identify the mechanisms causing this movement. In 1905, Albert Einstein published an article explaining in detail how the movement observed by Brown was the result of the pollen moving by individual water molecules. In 1923, the child prodigy and “father of cybernetics,” Norbert Wiener, wrote an article about differentiable spaces, where he approached this movement from mathematics, determined probability measures in the trajectory space, and using the concept of Lebesgue integrals, laid the foundation for stochastic analysis. Since then, in the mathematical community, the Brownian motion is also referred to as the Wiener process.

In 1938, Kiyoshi Ito, a graduate of Tokyo University, began working at the Bureau of Statistics, where in his free time he got acquainted with the works of Andrei Kolmogorov, the founder of modern probability theory, and Paul Levy, a French scientist, who studies various properties of Brownian motion at that time. He tries to combine Levi’s intuitive visions with Kolmogorov’s exact logic, and in 1942 he wrote the paper On Stochastic Processes and Infinitely Divisible Distribution Laws, in which he reconstructs from scratch the concept of stochastic integrals and the theory of stochastic differential equations describing motions caused by random events.

Ito integral for simple processes

Ito has developed a fairly simple method for constructing an integral. To begin, we define the Ito integral for a simple piecewise-constant process. $$$\ Delta (t)$ and then we extend this concept to more complex integrands. So let us have a split again. $$$\ Pi = \ {0 = t_0 <t_1 <\ dots <t_n = T \}$ . We believe the values $$$\ Delta (t)$ are constant at each interval $$$[t_j, t_ {j + 1})$

Imagine that $$$B (t)$ - is the value of any financial instrument at the time $$$t$ (Brownian motion can take negative values, so this is not a very good model for price movement, but for now we will ignore this). Also let $$$t_0, t_1, \ dots, t_ {n-1}$ - these are trading days (hours / seconds, not important), but $$$\ Delta (t_0), \ Delta (t_1,), \ dots, \ Delta (t_ {n-1})$ - these are our positions (the number of financial instruments on hand). We believe that $$$\ Delta (t)$ depends only on information known at the time $$$t$ . By information, I mean the trajectory of the Brownian motion up to this point in time. Then our income will be:

$$

$$I (t) = \ sum_ {j = 0} ^ k \ Delta (t_j) [B (t_ {j + 1} -B (t_j)] + \ Delta (t_k) [B (t) -B (t_k )].$$

Process $$$I (t)$ called Ito integral for a simple process $$$\ Delta (t)$ and we will write it down as

$$

$$I (t) = \ int_0 ^ t \ Delta (s) dB (s).$$

This integral has several interesting properties. The first and rather obvious: at the initial moment, his expectation at any point is zero:

$$

$$\ mathbb {E} [I (t)] = 0.$$

Moreover, the Ito integral is a martingale, but more on that later.

The calculation of the second moment / variance already requires additional calculations. Let him $$$D_j = B (t_ {j + 1}) - B (t_j)$ for $$$j = 1, \ dots, k-1$ and $$$D_k = B (t) -B (t_k)$ . Then we can rewrite the Ito integral in the form

$$

$$I (t) = \ sum_ {j = 0} ^ k \ Delta (t_j) D_j.$$

Taking advantage of the fact that $$$\ mathbb {E} [D_j] = 0$ and by that $$$D_j$ and $$$D_i$ independent for $$$i \ neq j$ we can calculate

$$

$$\ begin {aligned} \ mathbb {E} [I ^ 2 (t)] & = \ mathbb {E} \ Big [\ sum_ {j = 0} ^ k \ Delta ^ 2 (t_j) D_j ^ 2 + 2 \ sum_ {0 \ leq i <j \ leq k} \ Delta (t_i) \ Delta (t_j) D_iD_j \ Big] \\ & = \ sum_ {j = 0} ^ k \ mathbb {E} \ Big [\ Delta ^ 2 (t_j) D_j ^ 2 \ Big] + 2 \ sum_ {0 \ leq i <j \ leq k} \ mathbb {E} [\ Delta (t_i) \ Delta (t_j) D_iD_j] \\ & = \ sum_ {j = 0} ^ k \ mathbb {E} \ Big [\ Delta ^ 2 (t_j) \ Big] \ cdot \ mathbb {E} [D_j ^ 2] + 2 \ sum_ {0 \ leq i <j \ leq k} \ mathbb {E} [\ Delta (t_i) \ Delta (t_j) D_i] \ cdot \ mathbb {E} [D_j] \\ & = \ sum_ {j = 0} ^ {k-1} \ mathbb { E} \ Big [\ Delta ^ 2 (t_j) \ Big] (t_ {j + 1} -t_j) + \ mathbb {E} [\ Delta ^ 2 (t_k)] (t-t_k) \\ & = \ sum_ {j = 0} ^ k \ mathbb {E} \ Big [\ int_ {t_j} ^ {t_ {j + 1}} \ Delta ^ 2 (s) ds \ Big] + \ mathbb {E} \ Big [ \ int_ {t_k} ^ t \ Delta ^ 2 (s) ds \ Big] \\ & = \ mathbb {E} \ Big [\ int_ {0} ^ t \ Delta ^ 2 (s) ds \ Big]. \ end {aligned}$$

Equality

$$

$$\ mathbb {E} [I ^ 2 (t)] = \ mathbb {E} \ Big [\ int_0 ^ t \ Delta ^ 2 (s) ds \ Big]$$

called ito isometry .

And finally, the quadratic variation. Let's first calculate the variation on each interval. $$$[t_j, t_ {j + 1}]$ where values $$$\ Delta (t)$ are constant, and then add them all together. Take a split interval $$$t_j = s_0 <s_1 <\ cdots <s_m = t_ {j + 1}$ and consider

$$

$$\ begin {aligned} \ sum_ {i = 0} ^ {m-1} [I (s_ {i + 1}) - I (s_i)] ^ 2 & = \ sum_ {i = 0} ^ {m- 1} [\ Delta (t_j) (B (s_ {i + 1}) - B (s_i)) ^ 2 \\ & = \ Delta ^ 2 (t_j) \ sum_ {t = 0} ^ {m-1} (B (s_ {i + 1}) - B (s_i)) ^ 2 \\ & \ xrightarrow [m \ rightarrow \ infty] {} \ Delta ^ 2 (t_j) (t_ {j + 1} -t_j) \ \ & = \ int_ {t_j} ^ {t_ {j + 1}} \ Delta ^ 2 (s) ds. \ end {aligned}$$

The quadratic variation for the interval is considered similarly. $$$[t_k, t]$ . Summing up all these pieces, we get

$$

$$[I (t)] = \ int_0 ^ t \ Delta ^ 2 (s) ds.$$

Now we can clearly see the difference between variance and variation. If the process $$$\ Delta (t)$ is deterministic, they coincide. But if we decide to change our strategy depending on the trajectory along which the Brownian motion passed, then the variation will begin to change, while the variance is always equal to a certain value.

Ito integral for complex processes

Now we are ready to extend the concept of Ito integral to more complex processes. Let us have a function $$$h (t)$ which can continuously change in time and even have breaks. The only assumptions we want to preserve are the quadratic integrability of the process:

$$

$$\ mathbb {E} \ Big [\ int_0 ^ T h ^ 2 (t) dt \ Big] <\ infty$$

and adaptability , i.e. at the moment $$$t$ when we know the meaning $$$B (t)$ we should already know the meaning $$$h (t)$ . In the real world, we cannot first know the value of shares for tomorrow, and then invest in them.

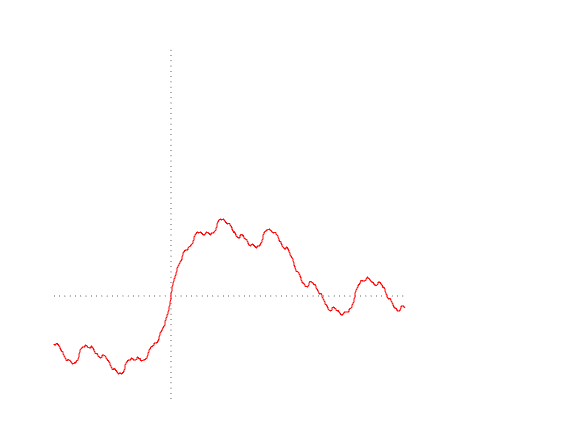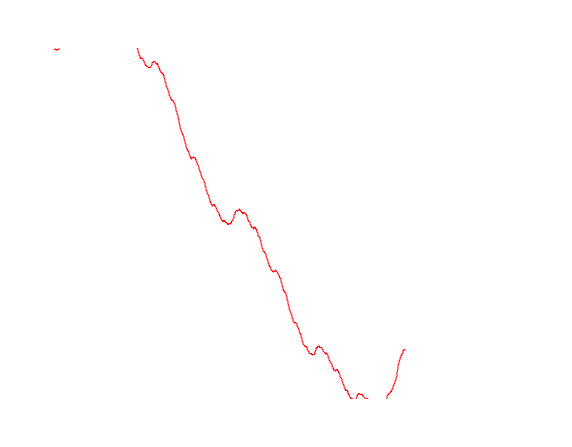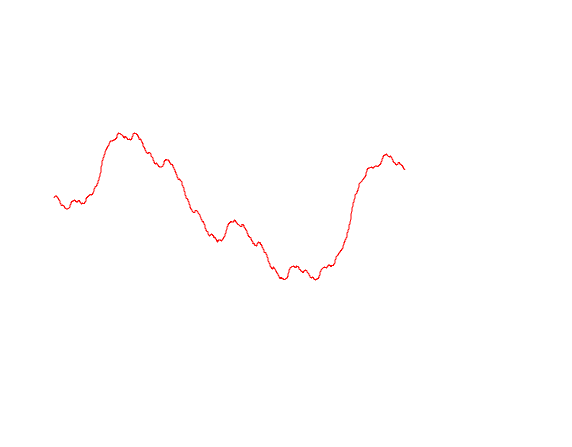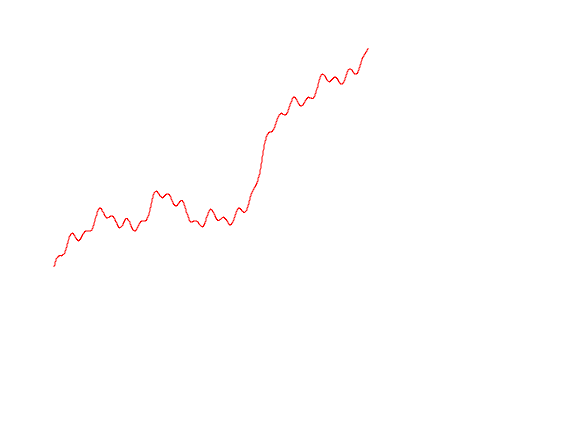
In order to determine $$$\ int_0 ^ T h (t) dB (t)$ we approximate $$$h (t)$ simple processes. The graph below shows how this can be done.


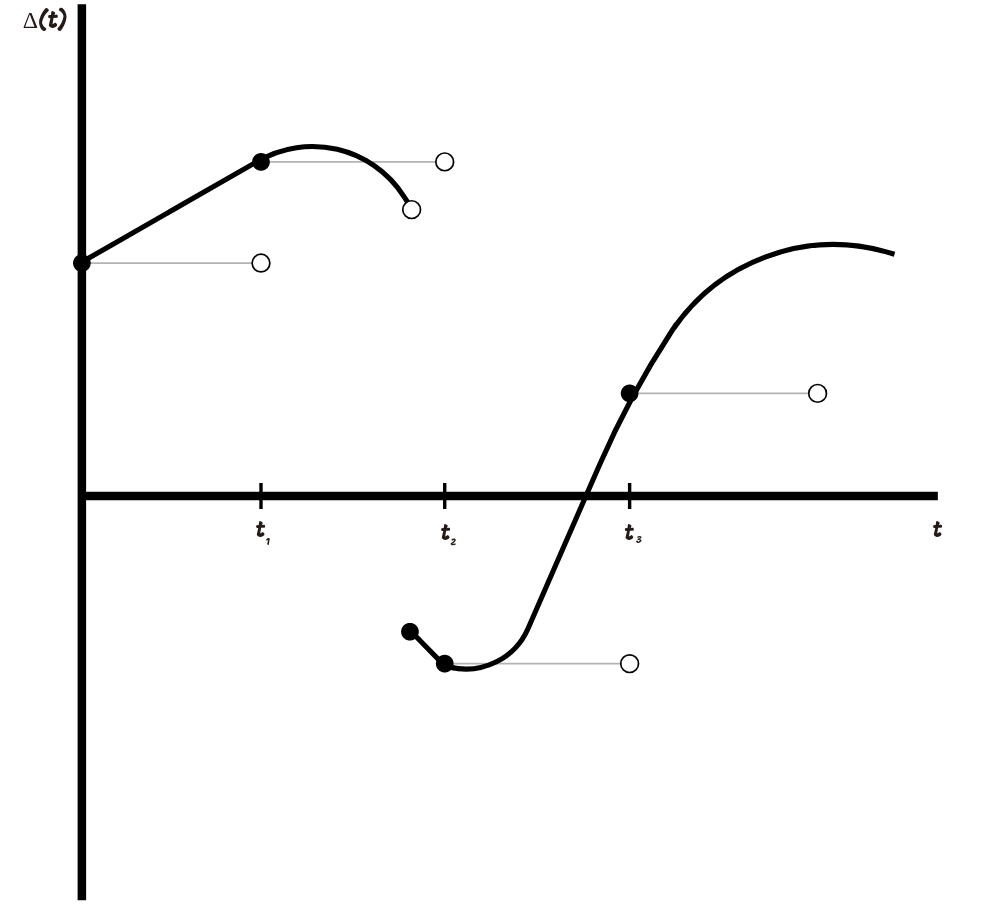
The approximation is as follows: we choose a partition $$$0 = t_0 <t_1 <t_2 <t_3$ then create a simple process whose values ​​are equal $$$h (t_j)$ for each $$$t_j$ and do not change on the segment $$$[t_j, t_ {j + 1})$ . The smaller the maximum step of our partition becomes, the closer the approximating simple process becomes to our integrand.

In general, it is possible to select a sequence of simple processes. $$$h_n (t)$ such that it will converge to $$$h (t)$ . By convergence we mean

$$

$$\ lim_ {n \ rightarrow \ infty} \ mathbb {E} \ Big [\ int_0 ^ T | h_n (t) -h (t) | ^ 2 dt \ Big] = 0.$$

For each process $$$h_n (t)$ The Ito integral is already defined and we define the Ito integral for a continuously changing process as the limit:

$$

$$\ int_0 ^ t h (s) dB (s) = \ lim_ {n \ rightarrow \ infty} \ int_0 ^ th_n (s) dB (s), \ quad 0 \ leq t \ leq T.$$

The Ito integral in general has the following properties:

• His trajectories are continuous.
• It is adapted. It is logical, because at every moment we must know our value of income.
• It is linear: $$$\ int_0 ^ t h (s) dB (s) + \ int_0 ^ t f (s) dB (s) = \ int_0 ^ t (h (s) + f (s)) dB (s).$
• He is a martingale, but more on that towards the end of the article.
• Ito’s isometry is preserved: $$$\ mathbb {E} [I ^ 2 (t)] = \ mathbb {E} \ Big [\ int_0 ^ t h ^ 2 (s) ds \ Big]$ .
• Its quadratic variation: $$$[I (t)] = \ int_0 ^ th ^ 2 (s) ds.$

A small remark: for those who want to study in more detail the construction of the Ito integral or in general is interested in financial mathematics, I strongly advise the book by Steven Shreve “Stochastic Calculus for Finance. Volume II.

How about?

For the following reasoning, we will denote the Ito integral in a slightly different form:

$$

$$I (h) = \ int_ {0} ^ T h (s) dB (s),$$

for some $$$T$ . Thus, we prepare ourselves for the idea that the Ito integral is a mapping acting from the space of square integrable functions $$$L ^ 2 ([0, T])$ in the probabilistic space of random processes. So for example, you can move from the old to the new notation:

$$

$$I (t) = \ int_0 ^ T h (s) \ cdot 1 _ {[0, t]} (s) ds = I (h \ cdot 1 _ {[0, t]}).$$

In the previous article, we implemented the Gaussian process: $$$W: H \ rightarrow L ^ 2 (\ Omega, \ mathcal {F}, \ mathbb {P})$ . We know that the Gaussian process is a mapping from a Hilbert space into a probabilistic one, which is essentially a generalized case of the Ito integral, a mapping from a space of functions into a space of random processes. Really,

 data L2Map = L2Map {norm_l2 :: Double -> Double} type ItoIntegral = Seed -- ω, random state -> Int -- n, sample size -> Double -- T, end of the time interval -> L2Map -- h, L2-function -> [Double] -- list of values sampled from Ito integral -- | 'itoIntegral'' trajectory of Ito integral on the time interval [0, T] itoIntegral' :: ItoIntegral itoIntegral' seed n endT h = 0 : (toList $ gp !! 0) where gp = gaussianProcess seed 1 (n-1) (\(i, j) -> norm_l2 h $ fromIntegral (min ij + 1) * t) t = endT / fromIntegral n 

The function itoIntegral ' takes as input the seed is a parameter for the random variable generator, n is the dimension of the output vector, endT is the parameter $$$T$ and the function h from the class L2Map, for which the function norm_l2 is defined , which returns the integrand rate: $$$t \ mapsto \ int_0 ^ t h ^ 2 (s) ds$ . At the output, itoIntegral issues an Ito integral implementation on the interval $$$[0, T]$ with a sampling rate corresponding to the parameter n . Naturally, a similar way of implementing the Ito integral is in a sense overkill, but it allows you to tune in to functional thinking, so necessary for further reasoning. We will write a faster implementation that does not require working with giant matrices.

 -- | 'mapOverInterval' map function f over the interval [0, T] mapOverInterval :: (Fractional a) => Int -- n, size of the output list -> a -- T, end of the time interval -> (a -> b) -- f, function that maps from fractional numbers to some abstract space -> [b] -- list of values f(t), t \in [0, T] mapOverInterval n endT fn = [fn $ (endT * fromIntegral i) / fromIntegral (n - 1) | i <- [0..(n-1)]] -- | 'itoIntegral' faster implementation of itoIntegral' function itoIntegral :: ItoIntegral itoIntegral seed 0 _ _ = [] itoIntegral seed n endT h = scanl (+) 0 increments where increments = toList $ (sigmas hnorms) * gaussianVector gaussianVector = flatten $ gaussianSample seed (n-1) (vector [0]) (H.sym $ matrix 1 [1]) sigmas s@(_:ts) = fromList $ zipWith (\xy -> sqrt(xy)) ts s hnorms = mapOverInterval n endT $ norm_l2 h 

Now using this function, we can implement, for example, the ordinary Brownian motion: $$$B (t) = \ int_0 ^ t dB (s)$ . The function h is a function whose norm_l2 norm will be $$$t \ mapsto \ int_0 ^ t ds = t$ , identical function.

 l2_1 = L2Map {norm_l2 = id} -- | 'brownianMotion' trajectory of Brownian motion aka Wiener process on the time interval [0, T] brownianMotion :: Seed -- ω, random state -> Int -- n, sample size -> Double -- T, end of the time interval -> [Double] -- list of values sampled from Brownian motion brownianMotion seed n endT = itoIntegral seed n endT l2_1 

Let's try to draw different versions of the trajectories of the Brownian motion.

 import Graphics.Plot let endT = 1 let n = 500 let b1 = brownianMotion 1 n endT let b2 = brownianMotion 2 n endT let b3 = brownianMotion 3 n endT mplot [linspace n (0, lastT), b1, b2, b3] 

It's time to double-check our previous calculations. Let's calculate the variation of the trajectory of Brownian motion on the interval $$$[0, 1]$ .

 Prelude> totalVariation (brownianMotion 1 100 1) 8.167687948236862 Prelude> totalVariation (brownianMotion 1 10000 1) 80.5450335433388 Prelude> totalVariation (brownianMotion 1 1000000 1) 798.2689137110999 

We can observe that with increasing accuracy, variation takes on more and more large values, while quadratic variation tends to $$$T = 1$ :

 Prelude> quadraticVariation (brownianMotion 1 100 1) 0.9984487348804609 Prelude> quadraticVariation (brownianMotion 1 10000 1) 1.0136583395467458 Prelude> quadraticVariation (brownianMotion 1 1000000 1) 1.0010717246843375 

Try running a variation calculation for arbitrary Ito integrals to make sure that $$$[I] (h) = \ int_0 ^ T h ^ 2 (s) ds$ regardless of the trajectory of movement.

Martingales

There is such a class of random processes - martingales . In order to $$$X (t)$ was a martingale, you must fulfill three conditions:

• It is adapted
• $$$X (t)$ almost everywhere of course:

  $$

  $$\ mathbb {E} [| X (t) |] <\ infty$$
• Conditional expectation of future values $$$X (t)$ equals its last known value:

  $$

  $$\ mathbb {E} [X (T) | X (t)] = X (t), \ quad t <T.$$

Brownian motion - martingale. The fulfillment of the first condition is obvious; the fulfillment of the second condition follows from the properties of the normal distribution. The third condition is also easily verified:

$$

$$\ mathbb {E} [B (T) | B (t)] = \ mathbb {E} [(B (T) -B (t)) + B (t) | B (t)] = B (t ).$$

The Ito integral is also a martingale (we leave the proof as an exercise). What does this tell us? Let us return to financial mathematics and imagine that the value of the stocks we have chosen is the Brownian motion (the assumption is rather naive, but still imagine), and $$$h (t)$ - this is our strategy, the number of shares in our portfolio. Process $$$h (t)$ may be accidental: we do not always know much in advance how many shares we want to keep, we will proceed from price movements $$$B (t)$ . But the main thing is that this process should be adapted, that is, at the moment $$$t$ we know exactly how many shares we have. We cannot go back in time and change this value. So, since the Ito integral is a martingale, it doesn’t matter which strategy we choose $$$h (t)$ On average, the gain from our trading will always go to zero.

There is another interesting theorem, the so-called martingale representation theorem : if we have a martingale $$$M (t)$ whose values ​​are determined by the Brownian motion, that is, the only process that introduces uncertainty in the values $$$M (t)$ , - this $$$B (t)$ then this martingale can be represented as

$$

$$M(t) = M(0) + \int_0^t H(s)dB(s),$$

besides the process $$$H(s)$is unique. In the future, when we increase the number of integrals and even expand them to non-adapted processes, this theorem will help us a lot.

And that's it for today.