Mixing colors

Mixing in OpenGL (and other graphical APIs, approx. Lane ) is the technique that is usually associated with the implementation of the transparency of objects. The translucency of an object implies that it is not filled with one solid color, but combines in different proportions the tint of its material with the colors of the objects behind it. As an example, you can take the colored glass in the window: the glass has its own shade, but in the end we see a mixture of the shade of the glass and all that is visible behind the glass. Actually, the term mixing arises from this behavior, since we observe the final color, which is a mixture of colors of individual objects. Due to this, we can see through translucent objects.







Semitransparent objects can be completely transparent (all colors pass through) or partially transparent (transmits light, but adds its own shade). In computer graphics, it is customary to denote the degree of opacity by the so-called alpha component of the color vector. The alpha component is the fourth element of the color vector and you must have noticed it more than once in previous lessons. However, up to this point we always kept this value equal to 1.0, which is equivalent to full opacity. By setting the alpha component to 0.0, we would achieve complete transparency. A value of 0.5 would mean that the final color of an object is 50% set by its material, and 50% is set by objects behind it.



All the textures that we used so far contained 3 components of color: red, blue and green. Some texture formats allow you to save also a fourth alpha component for each texel. This value indicates which parts of the texture are translucent and to what extent. For example, this window glass texture has an alpha component set at 0.25 for glass areas and 0.0 for a frame. In other conditions, the glass portions would be completely red, but due to 75% transparency, the color is mostly determined by the background of the current web page.





In the near future, we will add this texture to the new scene, but, for a start, we will discuss a simpler technique for achieving transparency in cases where either full transparency or complete opacity is needed.

Fragment Drop

In some cases, partial transparency is not required: you must either display something or nothing, based on the color value of the texture. Imagine a tuft of grass: the simplest implementation of a tuft would require grass texture on a 2D quad located in your scene. However, the quad form doesn’t really help the task of imitating a bunch of grass - we wouldn’t hurt to hide parts of the superimposed texture, leaving some others.



The texture presented below exactly represents the case described: its sections are either completely opaque (alpha component = 1.0), or completely transparent (alpha component = 0.0) - no means. You may notice that where there is no image of blades of grass you can see the background of the site, and not the color of the texture:





Thus, when placing vegetation in our scene, we would like to see only parts of the texture that correspond to parts of the plant, and discard the remaining parts of the texture that fill the polygon. That is, discard fragments containing transparent parts of the texture without storing them in a color buffer. But before we immediately mess our hands with fragments, you need to learn how to load textures with an alpha channel.



To do this, we don’t have to change much in the familiar code. The loader function from stb_image.h automatically loads the alpha channel of the image, if available. But you need to explicitly specify OpenGL when creating the texture, that it uses the alpha channel:

glTexImage2D(GL_TEXTURE_2D, 0, GL_RGBA, width, height, 0, GL_RGBA, GL_UNSIGNED_BYTE, data); 

Also make sure that in the fragment shader you are sampling a vector with 4 components, so as not to stay with only RGB values:

 void main() { // FragColor = vec4(vec3(texture(texture1, TexCoords)), 1.0); FragColor = texture(texture1, TexCoords); } 

Now that we’ve figured out loading textures with transparency, it's time to scatter a few grass tufts around the scene used in the depth test class.



Create a small vector that stores the position of grass tufts in the form glm :: vec3 :

 vector<glm::vec3> vegetation; vegetation.push_back(glm::vec3(-1.5f, 0.0f, -0.48f)); vegetation.push_back(glm::vec3( 1.5f, 0.0f, 0.51f)); vegetation.push_back(glm::vec3( 0.0f, 0.0f, 0.7f)); vegetation.push_back(glm::vec3(-0.3f, 0.0f, -2.3f)); vegetation.push_back(glm::vec3( 0.5f, 0.0f, -0.6f)); 

Each grass object is rendered as a single quad with the grass texture assigned to it. Not the most exciting method to imitate weed in 3D, but much more efficient than using polygonal models. With the help of small tricks, such as adding in the same position another pair of turned quads with the same texture, you can achieve good results.



As we assign the grass texture to the quad, we need a new VAO (vertex array object), fill in the VBO (vertex buffer object) and set the appropriate pointers to the vertex attributes. Further, after rendering the surface of the floor and cubes, we derive our grass:

 glBindVertexArray(vegetationVAO); glBindTexture(GL_TEXTURE_2D, grassTexture); for(unsigned int i = 0; i < vegetation.size(); i++) { model = glm::mat4(1.0f); model = glm::translate(model, vegetation[i]); shader.setMat4("model", model); glDrawArrays(GL_TRIANGLES, 0, 6); } 

The execution of the program will produce the following result:





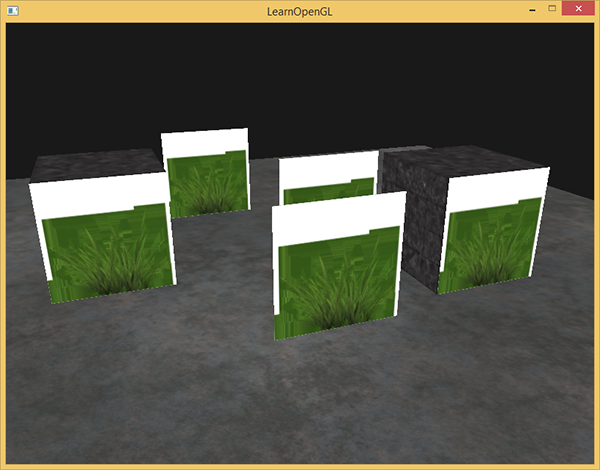
This happened because, by itself, OpenGL does not know what to do with the values ​​of the alpha channel, or when to discard fragments. All this we must specify manually. Fortunately, with shaders everything is pretty simple. In GLSL, there is a built-in discard directive, which, when invoked , terminates further processing of the current fragment without entering the color buffer. From here a solution emerges: check the value of the alpha component of the texture element and, if it is less than a certain threshold, discard it:

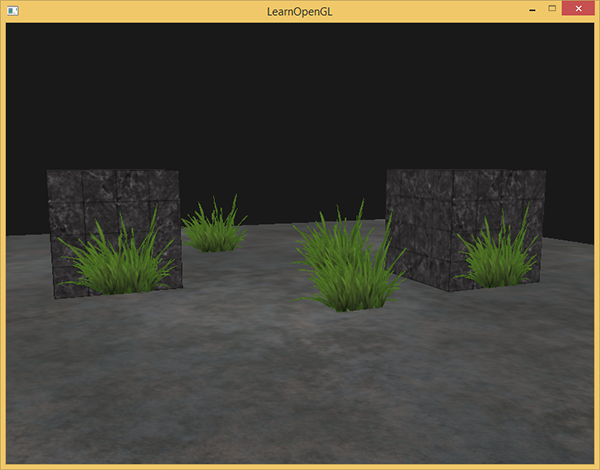
 #version 330 core out vec4 FragColor; in vec2 TexCoords; uniform sampler2D texture1; void main() { vec4 texColor = texture(texture1, TexCoords); if(texColor.a < 0.1) discard; FragColor = texColor; } 

In this code, we discard the fragment if the alpha component of the texture sample was less than 0.1. Such a shader will provide us with the output of only those fragments that turned out to be rather opaque:

Note that when sampling at texture boundaries, OpenGL interpolates the value at the border with the value of the value following it, obtained by repeating the texture (since we set the texture repeat parameter in GL_REPEAT ). This is normal for normal use of textures, but not suitable for our texture with transparency: a completely transparent value of texels at the upper border is mixed with fully opaque texels at the lower border. As a result, a translucent colored frame may appear around the quad with our texture. To avoid this artifact, you need to set the repeat option in GL_CLAMP_TO_EDGE when using textures with transparency.

 glTexParameteri( GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE); glTexParameteri( GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE); 

The example code is here .

Mixing

Despite the fact that dropping fragments is a convenient and simple way, it does not allow for the use of partial mixing of translucent colors. To render images with objects that have different degrees of opacity, we must turn on blending mode. This is done, as for most OpenGL modes:

 glEnable(GL_BLEND); 

Now, having turned on the mixing, it is worth understanding how exactly this works.

OpenGL mixing is performed using the following formula.

$$$$ display $$ \ begin {equation} \ bar {C} _ {result} = \ bar {\ color {green} C} _ {source} * \ color {green} F_ {source} + \ bar {\ color {red} C} _ {destination} * \ color {red} F_ {destination} \ end {equation} $$ display $$

Where $$$\ bar {\ color {green} C} _ {source}$- vector color source. This is the color value obtained from the texture.

$$$\ bar {\ color {red} C} _ {destination}$- vector color receiver. This is the color value currently stored in the color buffer.

$$$\ color {green} F_ {source}$- source multiplier. Sets the degree to which the alpha component affects the color of the source.

$$$\ color {red} F_ {destination}$- receiver multiplier. Sets the degree to which the alpha component affects the color of the receiver.



After the execution stage of the fragment shader and other tests (stencil and depth tests, approx. Lane ), this mixing formula is free to do anything with the colors of the processed fragments and colors stored in the buffer at the current moment (the color values ​​of the fragments from the previous frame). The source and destination roles are assigned to OpenGL automatically, but we can set the factors for them ourselves. First, consider the following example:





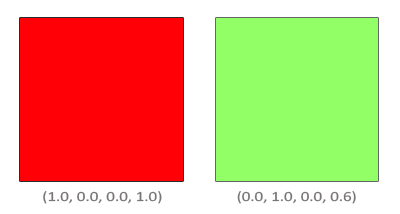
There are two squares and translucent green we would like to draw over opaque red. In this case, the receiving color will be the color of the red square, which means that it should be first buffered in the color buffer.



The question arises: how to choose the values ​​of the factors in the mixing formula? Well, at least we should multiply the green color of the second square by its value of the alpha component, therefore, $$$\ color {green} F_ {source}$Let us take the alpha component of the source color vector, i.e. 0.6. Based on this, it is reasonable to assume that the receiver will provide a contribution to the result proportional to the degree of transparency remaining available. If the green square provides 60% of the total, then the red square should get 40% (1. - 0.6). So the multiplier $$$\ color {red} F_ {destination}$set equal to the difference unit and the alpha components of the source color vector. As a result, the expression of mixing takes the following form:

$$$$ display $$ \ begin {equation} \ bar {C} _ {result} = \ begin {pmatrix} \ color {red} {0.0} \\ \ color {green} {1.0} \\ \ color {blue} {0.0} \\ \ color {purple} {0.6} \ end {pmatrix} * \ color {green} {0.6} + \ begin {pmatrix} \ color {red} {1.0} \\ \ color {green} {0.0 } \\ \ color {blue} {0.0} \\ \ color {purple} {1.0} \ end {pmatrix} * \ color {red} {(1 - 0.6)} \ end {equation} $$ display $$

The result of mixing will be the color of 60% consisting of the original green and 40% of the original red - this is a vague brown color:





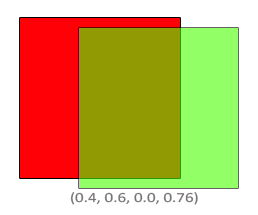
The result will be buffered in color, replacing the old values.

Well, how can we let OpenGL know what values ​​of mixing coefficients we want to use? Fortunately, there is a special feature:

 glBlendFunc(GLenum sfactor, GLenum dfactor) 

It takes two parameters that determine the values ​​of the source and receiver coefficients. The OpenGL API defines an exhaustive list of the values ​​of these parameters, allowing you to customize the blend mode as you please. Here I will give the most "running" values ​​of the parameters. I note that the constant color vector $$$\ bar {\ color {blue} C} _ {constant}$set separately by the glBlendColor function.





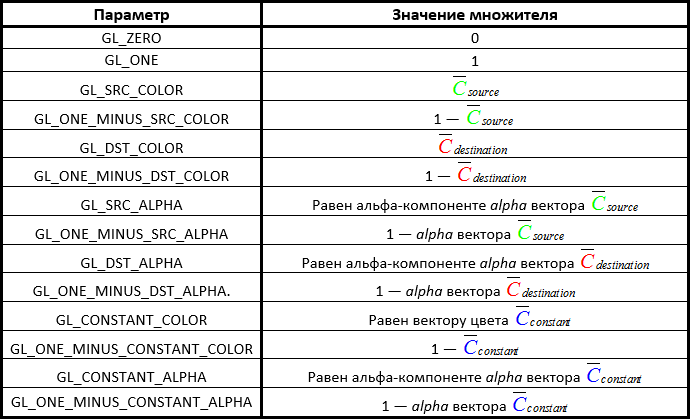
To get the result described in the example with two squares, we need to choose parameters such that the source coefficient equals the alpha (alpha value) of the source color, and the receiver coefficient equals 1 - alpha . Which is equivalent to calling:

 glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA); 

It is also possible to separately adjust the coefficients for the RGB and alpha components through the function glBlendFuncSeparate :

 glBlendFuncSeparate(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA, GL_ONE, GL_ZERO); 

Such a call adjusts the mixing of the RGB component as in the previous example, additionally indicating that the alpha component of the result will be equal to the alpha component of the source.

OpenGL allows even more flexible setting of the blending formula, allowing the choice of the operation between the components of the formula. By default, the source and receiver components add up, but you can choose and subtract, if that is the intention. Defines the behavior of the function

 glBlendEquation(GLenum mode) 

And there are three options available for the parameter:

• GL_FUNC_ADD : default value, adds components: $$$\ bar {C} _ {result} = \ color {green} {Src} + \ color {red} {Dst}$.
• GL_FUNC_SUBTRACT : subtracts the receiver component from the source component: $$$\ bar {C} _ {result} = \ color {green} {Src} - \ color {red} {Dst}$.
• GL_FUNC_REVERSE_SUBTRACT : subtracts the source component from the receiver component: $$$\ bar {C} _ {result} = \ color {red} {Dst} - \ color {green} {Src}$.

Normally, calling glBlendEquation is not required, since the default mode GL_FUNC_ADD is suitable for most applications. But for non-standard approaches and attempts to create an unusual visual solution, other modes of calculating the mixing formula may also be useful.

Render of translucent textures

So, we got to know how the library performs mixing. It's time to put this knowledge into practice by creating a couple of transparent windows. We use the same scene as at the beginning of the lesson, but instead of grass tufts we place objects with the window texture already mentioned at the beginning of the lesson.



To begin, turn on the blending mode and select its parameters:

 glEnable(GL_BLEND); glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA); 

Since we have enabled blending, there is no longer any need to drop transparent fragments. The fragment shader code will be returned to the previous state:

 #version 330 core out vec4 FragColor; in vec2 TexCoords; uniform sampler2D texture1; void main() { FragColor = texture(texture1, TexCoords); } 

Now, when processing each OpenGL fragment, it mixes the color of the fragment being processed and the color stored in the buffer according to the value of the alpha component of the first one. Since the glass part of the window is translucent, we should see the rest of the scene behind the window:





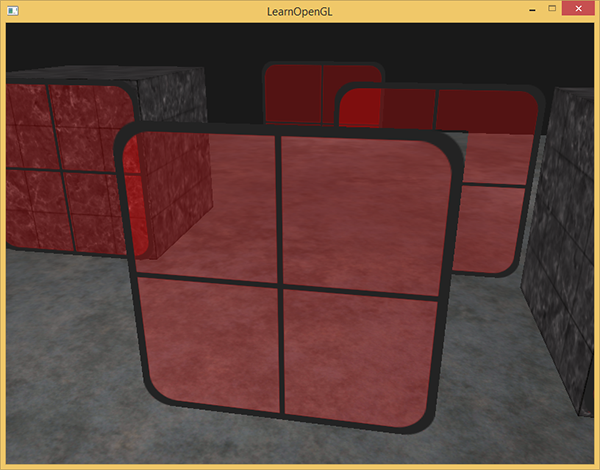
However, after looking closely, you can see that the render is incorrect. For some reason, the translucent parts of the window closest to us overlap the other windows in the background!

The reason is that the depth test does not take into account whether the fragment is transparent or not during processing. As a result, all quad fragments with a window texture pass the depth test in one way, whether they belong to the glass part or not. Despite the fact that behind the glass parts the old fragments of the depth test should remain, they will be rejected.



Bottom line: you can not display translucent objects anyhow and hope that the depth test and mixing themselves decide how to do everything correctly. In order to ensure the correct rendering of windows overlapped by other windows, we need to first output the windows lying in the distance. Thus, we need to sort the windows ourselves by the position from the farthest to the closest ones and display them in accordance with this procedure.

I note that for cases with full transparency (the case with grass), the operation of discarding fragments does not cause the problem described, since mixing does not occur.

Render with preservation order

For the mixing to work correctly when rendering a set of objects, you must start the output from the farthest and end the closest one. Non-transparent objects that do not require mixing can be displayed in a familiar manner using the depth buffer; no sorting is required here. But the opaque part of the scene must be drawn before elements that use blending are displayed. As a result, the procedure for rendering a scene containing both opaque and transparent objects is as follows:

1. Print all opaque objects.
2. Sort transparent objects by deletion.
3. Draw transparent objects in sorted order.

One sort of sorting method is ordering based on the distance from the object to the observer. This value is defined as the distance between the position vectors of the camera and the object itself. Next, we will save this distance together with the object's position vector in the map container of the standard C ++ library. The associative container map will automatically arrange the ordering of the stored items based on the key values, so we only need to fill in all the distance-position pairs of the objects:

 std::map<float, glm::vec3> sorted; for (unsigned int i = 0; i < windows.size(); i++) { float distance = glm::length(camera.Position - windows[i]); sorted[distance] = windows[i]; } 

As a result, we will have a container with the positions of the window objects sorted by the distance from the smallest to the largest.



At the time of rendering, we need to go through the container in the reverse order (from the greatest distance to the lowest) and draw the windows in the corresponding positions:

 for(std::map<float,glm::vec3>::reverse_iterator it = sorted.rbegin(); it != sorted.rend(); ++it) { model = glm::mat4(1.0f); model = glm::translate(model, it->second); shader.setMat4("model", model); glDrawArrays(GL_TRIANGLES, 0, 6); } 

Here we use the inverse iterator for the container to allow it to go through in the reverse order. Each object of the window at the same time is shifted to the appropriate position and drawn. A relatively simple modification of the code led to the complete resolution of the previously identified problem:





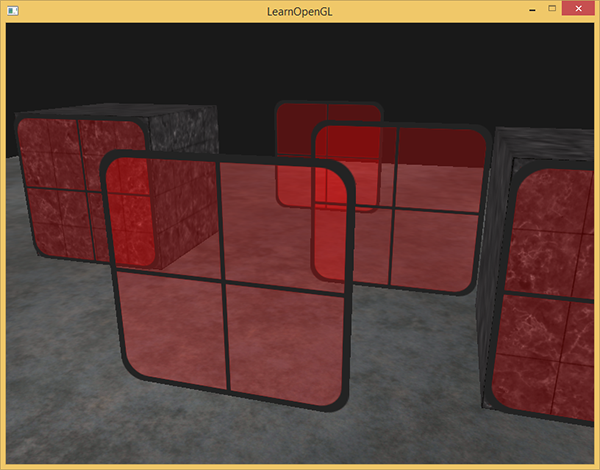
As you can see, the scene is now displayed correctly. The source code of the example is here .

It should be noted that a simple sorting by range, although it worked well in this case, but does not take into account such features as turns, scaling and other transformations of objects. Also objects of complex shape would require a more sophisticated metric for sorting, rather than just distance from the camera.



In addition, the sorting is not given for free: the complexity of this task is determined by the type and composition of the scene, and the process itself requires additional computational costs. There are also more advanced methods for outputting scenes containing both transparent and non-transparent objects: for example, the Order Independent Transparency (OIT ) algorithm. But the coverage of this topic is beyond the scope of the lesson. And you have to do with the usual implementation of mixing. But there is no reason for sadness, knowing the limitations of technology and being careful, you can achieve quite impressive results!



PS : And again in the comments useful link . You can see how the selection of blend modes affects the total.

PPS : We have a telegram-conf with eanmos to coordinate transfers. If there is a serious desire to help with the translation, then you are welcome!