Three, seven, joker - analysis of the solution of problems from the GridGain booklet at the Joker 2017 conference

t - the duration of the action in minutes,

r - the number of written lines of code in time t,

k is the number of nods during time t.



$$$t <60$

$$$r = 100$

$$$k = 243$

$$$f (x) = r / t$

$$$x = k / t$



$$$r / t = 1 + sqrt (k / t)$



Replace $$$1 / t = y$

$$$ry = 1 + sqrt (ky)$

$$$ry - 1 = sqrt (ky)$

$$$r ^ 2 * y ^ 2 - 2ry +1 = ky$

$$$r ^ 2 * y ^ 2 - (2r + k) y + 1 = 0$



Solve the usual quadratic equation: discriminant, root, two possible solutions:

$$$D = (2r + k) ^ 2 - 4r ^ 2 = $ 156,24$

$$$sqrt (D) = 395,2834426$

$$$y = ((2r + k) ± sqrt (D)) / 2r ^ 2$



$$$y1 = 0.041914172$

$$$y2 = 0,002385828$



Replace back:

$$$t1 = 23.8582787$

$$$t2 = $ 419.141721$



and choose one root that satisfies the condition t1 <60, which is substituted into the equation:

$$$x = k / t1 = $ 10.1851438$



Answer: 10,185

We have a number system with a base of 10 + 33 = 43







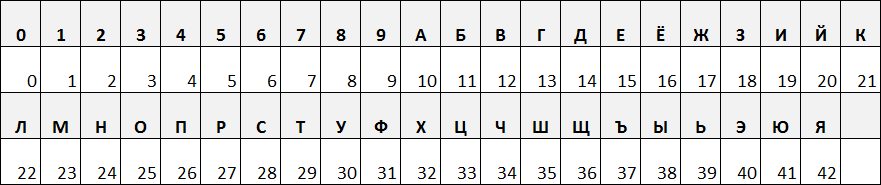
We bring Cyrillic numbers to decimal representation:



POST = {26, 25, 28, 29} = (((26 * 43) + 25) * 43 + 28) * 43 + 29 = 2114640



Similarly:



REPENT = {26, 25, 21, 10, 20, 28, 42} = 168103278466

PRAYER = {23, 25, 22, 19, 29, 12, 10} = 149143339604



REPENT + PRAYER * POST = 315384639763481026



We give the decimal result to the Cyrillic representation, for this we are looking for the first most significant digit, which will be zero:



$$$43 ^ {11} = 929293739471222707> 315384639763481026$

$$$43 ^ {10} = 21611482313284249 <315384639763481026$



Consistently divide the remainder by 43 to the power of 10 to 0:



$$$315384639763481026/43 ^ {10} = $ 1$

$$$12823887377501540/43 ^ 9 = $ 2$

$$$259072079080465/43 ^ 8 = $ 2$

$$$1931672973243/43 ^ 7 = $$

$$$28,942,695494 / 43 ^ 6 = 4$

$$$3657243298/43 ^ 5 = $ 2$

$$$129040666/43 ^ 4 = $ 3$

$$$2545029/43 ^ 3 = $ 3$

$$$805/43 ^ 2 = 0$

$$$805/43 ^ 1 = 18$

$$$31/43 ^ 0 = 31$



{14, 25, 22, 7, 4, 24, 37, 32, 0, 18, 31} = DOL74NbH0ZF



Answer: DOLL74NH

Given the initial conditions, we calculate the number of possible combinations:



Hermann: 2 aces out of 4 = $$$C ^ 2_4$= 6.

Old Woman: 2 peaks out of 9 numeric = $$$C ^ 2_9$= 36

Flop: 3 cards from the remaining 48 in the deck = $$$C ^ 3_ {48}$= 17296.

In total there are 6 * 36 * 17296 = 3735936 combinations.



Now consider the appropriate options.



Hermann in all variants also: 2 aces out of 4 = $$$C ^ 2_4$= 6.

Options with the hand of the old woman:

1) no 3 and 7 in hand, 2 out of 7 = $$$C ^ 2_7$= 21.

2) one 3 or 7 in the hand, it is 2 * 7 combinations = 14.

3) and 3 and 7 in hand = 1.



We check that we considered all combinations 21 + 14 + 1 = 36.



Now we find the number of suitable combinations for the flop:



1) There are 2 aces, 4 triples and 4 sevens in the deck = 2 * 4 * 4 = 32 combinations.

2) there are 2 aces left in the deck, 3 cards of one number and 4 other = 2 * 3 * 4 = 24 combinations.

3) There are 2 aces, 3 triples and 3 sevens in the deck = 2 * 3 * 3 = 18 combinations.



Total number of matching combinations:

6 * 21 * 32 + 6 * 14 * 24 + 6 * 1 * 18 = 6156



The desired probability is 6156/3735936 = 0.00164777983348751156336725254394



Answer: 0.00165 or 0.165%