Depth buffer

In the lesson on coordinate systems , we rendered a three-dimensional container using the depth buffer, which prevented the erroneous derivation of faces behind the others. In this lesson, we take a closer look at the depth buffer (or z-buffer) and the values ​​stored in it, as well as find out exactly how the test passes if the fragment is behind the others.





The depth buffer as well as the color buffer (which stores the colors of all the fragments — the visible image) stores certain information for each fragment and usually has the same dimensions as the color buffer. The depth buffer is created automatically by the OS window system and stores the values ​​as 16, 24, or 32 bit floating point numbers. In most systems, a default buffer is created with an accuracy of 24 bits.



When the depth test is enabled, OpenGL checks the depth of each fragment being processed against the data stored in the buffer. When passing the test, the buffer contents will be updated with the value of the depth of the fragment being processed, if the test fails, the stored value will remain the same and the fragment will be discarded.



The depth test is performed in screen space after the fragment shader is executed (and after the stencil test, which will be discussed in the next lesson). The screen coordinates are directly related to the viewport parameters specified by the glViewport function, and are available via the built-in GLSL variable gl_FragCoord in the fragment shader code. The x and y components of this variable are the coordinates of the fragment in the viewport (the lower left corner of the window has coordinates (0, 0)). Gl_FragCoord also has a third component, which actually contains the fragment depth value. This z-component is used to compare values ​​from the depth buffer.

Modern GPUs almost all use a trick called the early depth test. This technique allows you to perform a depth test before performing a fragment shader. If it becomes known to us that this fragment cannot be seen in any way (blocked by other objects), then we can discard it before the shading stage.

Fragment shaders are quite computationally heavy, so you should avoid executing them where it is meaningless. This technique has only one limitation: the fragment shader should not change the value of the fragment depth. This is obvious, because OpenGL in this case will not be able to determine in advance the value of the depth of the fragment being processed.

By default, the depth test is disabled. Turn it on:

glEnable(GL_DEPTH_TEST); 

Now, with the depth test turned on, OpenGL will automatically save the depth values ​​for all the passed test fragments and discard those not passed.



Turning on the depth test also requires clearing the buffer from the old values ​​in each frame. A new GL_DEPTH_BUFFER_BIT flag is added to the familiar glClear function .

 glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); 

In certain situations, you may need to perform a depth test for the processed fragments with their dropping according to the test results, but without updating the contents of the buffer itself. Those. assigning a read-only mode to the buffer. Writing to the buffer is disabled by setting the depth mask to GL_FALSE :

 glDepthMask(GL_FALSE); 

I note that this only makes sense when the depth test is on.

Depth test function

OpenGL allows you to override the comparison operator used in the depth test, which gives us a subtle control over which fragments should be processed, which ones to drop and in which cases the depth buffer will be updated. The operator is set by calling the function glDepthFunc :

 glDepthFunc(GL_LESS); 

The function accepts the ID of the comparison operator from this list:





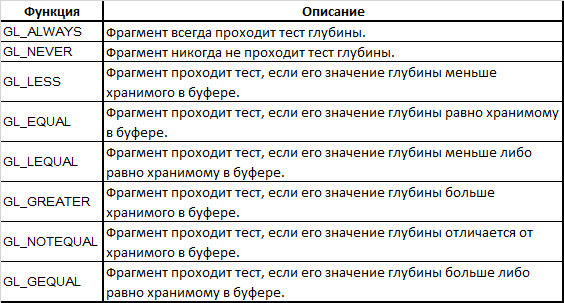
The default is GL_LESS , which means dropping all fragments that have a depth greater than or equal to the depth value stored in the buffer.



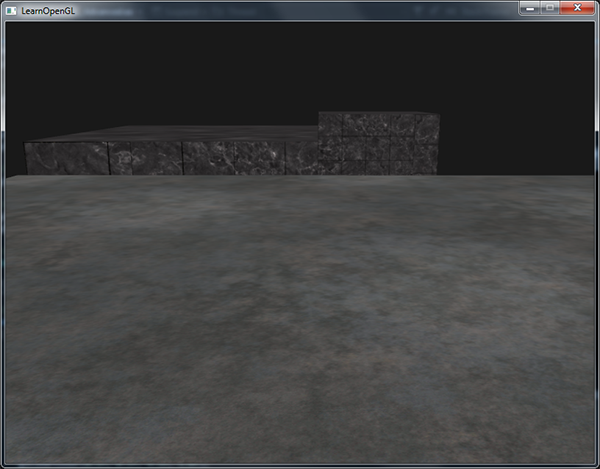
Let's experiment with how different comparison operators affect the output of our application. We use a new project that sets the stage with two textured cubes standing on the floor and not using lighting. The source code is here . First, let's change the operator to GL_ALWAYS :

 glEnable(GL_DEPTH_TEST); glDepthFunc(GL_ALWAYS); 

This setting is equivalent to turning off the depth test, which ultimately simply displays fragments that were later processed on top of those that were processed earlier, even if they should have been in the foreground. And since we draw the floor last, its fragments and overlapped all previously derived cube fragments:





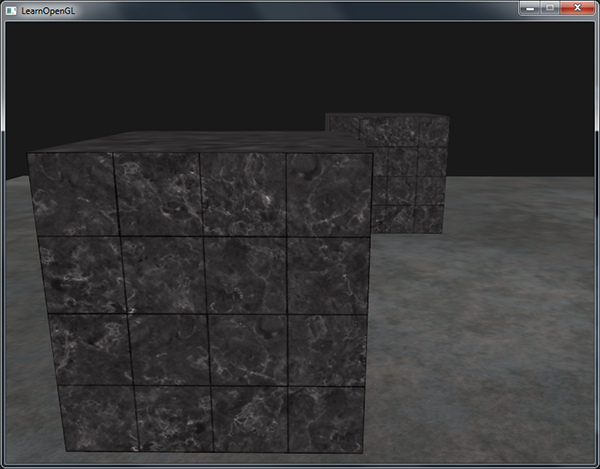
Returning the GL_LESS statement back, we get the correct scene:

The issue of depth accuracy

The values ​​in the depth buffer are limited by the interval [0.0, 1.0] and the z-components of all objects of the scene are checked against them from the observer's point of view. In this case, the z-component of the object in the species space can take any value in the interval [zNear, zFar], which determines the near and far boundary of the projection pyramid ( projection frustum ). To eliminate this inconsistency, we need a way to convert the values ​​of z-components in the species space to the interval [0.0, 1.0]. The first, naive method is a simple linear transformation:

$$

$${{F} _ {depth}} = \ frac {z-zNear} {zFar-zNear}$$

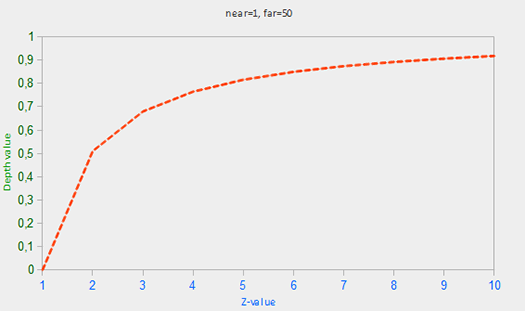
where zNear and zFar are the values ​​of the near and far parameters that we used when constructing the projection matrix defining the visibility pyramid (see coordinate systems ). This relationship takes as a parameter the value of z lying inside the visibility pyramid and converts it to the interval [0.0, 1.0]. The relationship between the z value and the resulting depth value can be seen in the graph:

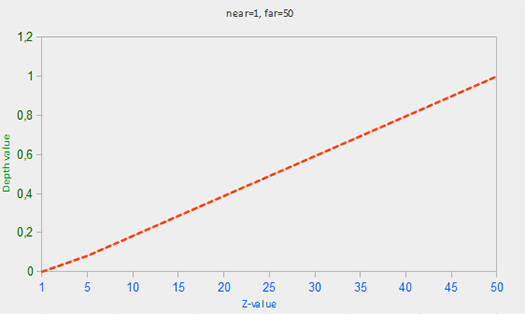
Note that all the dependencies considered give a value that tends to 0.0 for close objects and tends to 1.0 for objects lying near the far clipping plane.

However, in practice, the linear depth buffer is practically not used. To achieve a high-quality projection result, a relationship proportional to 1 / z is used. The result of using such a relationship is a high accuracy of depth values ​​for small z and a much lower accuracy for large z. Consider the meaning of this behavior: is the accuracy of the depth values ​​for objects removed by thousands of conventional units from the observer as with the detailed objects right in front of the observer important to us? The use of linear transformation does not take into account this question.



Since the nonlinear transformation is proportional to the 1 / z value, then for z values ​​in the interval [1.0, 2.0] we get depth values ​​in the interval [1.0, 0.5], which already covers half of the float accuracy, providing tremendous accuracy for small z. Values ​​of z from the interval [50.0, 100.0] will be provided for only 2% of the available float accuracy - but this is exactly what we need. So, the new dependence, including taking into account both the parameters zNear and zFar of the projection matrix:

$$

$${{F} _ {depth}} = \ frac {1 / z-1 / zNear} {1 / zFar-1 / zNear} \, \, \, \, \, \, \, \, (2)$$

Do not worry if it is not clear to you what exactly this expression implies. The main thing is to remember that the values ​​stored in the depth buffer are non-linear in the screen space (in the species space, before applying the projection matrix, they are linear). A value of 0.5 in the buffer does not mean that the object is located in the middle of the visibility pyramid. In fact, the point to which this depth corresponds is rather close to the near cut-off plane. The graph below shows the considered dependence of the non-linear depth value on the initial value of the z-component:





As you can see, the depth values ​​vary greatly for small input z, giving us increased accuracy in the region near the near cut-off plane. The expression itself of transforming the values ​​of z (from the observer's point of view) is embedded in the structure of the projection matrix. Thus, when we translate the coordinates of the vertices from the species space into the clipping space (clips space) and further into the screen space, we apply a non-linear transformation of the values ​​of z. If you want to understand the details of the mechanics of the projection matrix, I recommend this wonderful article .



The effect of nonlinearity is easy to notice when trying to visualize the depth buffer.



A visual representation of the depth buffer values.



So, in the vertex shader we have access to the value of the fragment depth through the z-component of the built-in variable gl_FragCoord . If we output this value as a color value, then we will be able to visualize the contents of the current depth buffer:

 void main() { FragColor = vec4(vec3(gl_FragCoord.z), 1.0); } 

If you try to start the application, then, most likely, everything will be filled with white color, giving the impression that all objects have a depth of 1.0 - the maximum possible value. Why do we not see the darker areas, where the depth approaches zero?



From the previous section, we remember that in the screen space, the depth buffer values ​​are non-linear, i.e. for small z, the accuracy is high, and for large z it is small. The depth value very quickly increases with the distance in the scene, because almost all the vertices quickly reach depths close to 1.0. If we carefully move closer to one of the objects, we will eventually be able to distinguish the darkening of their near parts with a decrease in the value of z:



This clearly shows the non-linear nature of the depth values. For nearby objects, the depth value changes much faster than with distant ones. The slightest movement of the camera changes colors from almost black to pure white.



We, however, have the ability to convert nonlinear fragment depth values ​​back to linearly distributed ones. To do this, we need to literally reverse the projection process, but only for depth values. The first step is to convert the depth values ​​back from the interval [0.0, 1.0] to the interval [-1.0, 1.0] corresponding to the normalized device coordinates ( NDC, normalized device coordinates ) of the clipping space. Then we derive the expression inverse to the nonlinear expression (2) and apply it to the obtained depth value. The result will be a linear depth value. It sounds quite usable, how do you think?



So, first, let's translate the depth value into NDC:

 float z = depth * 2.0 - 1.0; 

Further, we transform the obtained value of z into a linear one using the inverse (2) dependence:

 float linearDepth = (2.0 * zNear * zFar) / (zFar + zNear - z * (zFar - zNear)); 

Recall that this expression was obtained for projection matrices using expression (2) for nonlinear transformation of depth values, also limiting them to the interval [zNear, zFar]. I reiterate a link to an article full of mathematical details of the internal structure of the projection matrix. Also from the article one can understand where the above expression comes from.



The full text of the fragment shader that converts nonlinear depth values ​​in the screen space to linear ones:

 #version 330 core out vec4 FragColor; float zNear = 0.1; float zFar = 100.0; float LinearizeDepth(float depth) { //    NDC float z = depth * 2.0 - 1.0; return (2.0 * zNear * zFar) / (zFar + zNear - z * (zFar - zNear)); } void main() { //   zFar    float depth = LinearizeDepth(gl_FragCoord.z) / zFar; FragColor = vec4(vec3(depth), 1.0); } 

Since the linearized depth values ​​are between the borders of zNear and zFar, most of the values ​​will be greater than 1.0 and will be displayed as a pure white color. Dividing the linear depth value by the value of zFar in the code of the main function, we approximate it to the interval [0.0, 1.0]. This will allow us to observe a smooth increase in the brightness of the objects of the scene with their approach to the far plane of the pyramid of the projection, which is much clearer.



By launching the application at this time, you can be sure of the linear nature of the change in depth values ​​with distance. Try to wander around the scene in order to observe the changes:

The scene is almost completely filled with black color, since the depth values ​​vary linearly from zNear = 0.1 to zFar = 100.0, which, in this case, is quite far away. And since we are close to the near plane of the pyramid of the projection, the depth values ​​and, accordingly, the brightness are very small.

Depth Buffer Limited Precision Artifacts

A visual artifact is quite common, appearing in cases where two planes or two triangles are superimposed on each other so closely that the accuracy of the depth buffer is not enough for an unambiguous resolution of the order of location of these objects. As a result of this ambiguity, the fragments of these objects constantly seem to change the order of arrangement, creating visual noise and patterns. The phenomenon is called z-fighting , because it looks as if the displayed figures are fighting for the possibility of overlapping another.



In the scene used, there are enough places where z-fighting is noticeable: the containers are specifically located at the same height as the floor, ensuring that the floor and the bottom of the container are in the same plane. This also means that the depth values ​​for both planes are equal, which makes it impossible to use the depth buffer to resolve the order of these planes.



If you stick the camera in one of the containers, that effect will appear in all its glory. You can see how fragments of the floor plane constantly slip through the bottom of the box, creating an annoying ragged pattern: Z-fighting is a common problem when using the depth buffer and, typically, is more noticeable for remote objects (since at a distance the accuracy of the buffer decreases). We cannot completely avoid this phenomenon, but there are several approaches in the developer’s arsenal to reduce or completely get rid of z-fighting in a particular scene.

Coping methods

The first and perhaps most important piece of advice would never be to place objects too close to each other, with the risk of overlapping triangles . By adding a small, invisible to the user, the offset between the objects, you will ensure your freedom from z-fighting. In our case with a plane and containers, it would be enough just to shift the containers in the direction of the positive semiaxis Y. A sufficiently small offset would be invisible, but sufficient to get rid of the artifact. However, this method requires manual scene modification and thorough testing to ensure that there are no z-fighting manifestations in the scene.



Another approach is to define the near cut plane as far as possible . As noted above, considerable accuracy is provided near the zNear plane. Therefore, if we move the near plane away from the observer, we will provide with greater accuracy the entire volume of the pyramid of visibility. However, it is worth remembering that excessive displacement of the near plane can lead to a noticeable truncation of objects in the vicinity. So this approach requires a certain amount of trial and adjustment in order to successfully select the value of zNear.



The third method simply suggests using the depth buffer format with greater precision , for which you will have to pay a fraction of the performance. In most cases, 24-bit precision buffers are used, but modern video cards also allow 32-bit precision for the depth buffer. Additional accuracy will reduce the effect of z-fighting, but it will cost you speed.



These three techniques for getting rid of z-fighting are the most common and easy to implement. There are other ways that are more laborious, but still do not guarantee complete relief from the problem. Indeed, z-fighting is a typical problem, but with careful use of these techniques, you probably won't have to deal with the manifestations of this artifact at all.



PS : one of the commentators of the original article gives a hint about two methods of eliminating z-fighting from 100%: using the stencil buffer when rendering in several approaches; and using the SGIX_reference_plain extension.