Not a simple coordinate system, but a gold one.
In one of the Penrose mosaics, only two diamonds with different angles are used. From these elements it is possible to build an aperiodic mosaic of any size. To display it, I tried to present the coordinates analytically.

The distribution of angles in a diamond in one is 1: 4, 36 °: 144 °, in the other 2: 3, 72 °: 108 °. Diamond angles are multiples of one-tenth of a full turn, 36 °.
Determine the coordinates of the corners of a regular decagon.
')
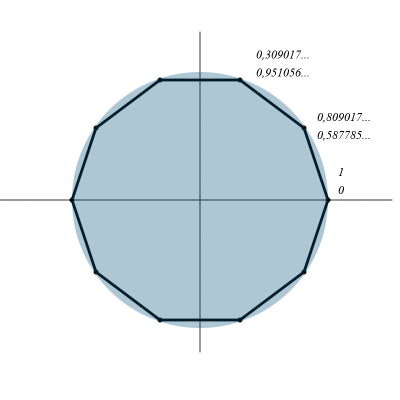
The rest are symmetrical, only the sign changes.
It is immediately noticeable that the cosines of the angles 36 ° and 72 ° differ by 0.5. And this is a very significant fact!
The absolute values of the coordinates are exactly three pieces, both for the abscissa and ordinate coordinates. All three can be represented as two coefficients with integer multipliers.
For the abscissa coordinates, it is simple: among the values are zero, which is represented by zero multipliers. Among the ordinate coordinates, the third — one — is not commensurate with the other two. But, since the difference in coordinates is 0.5, this difference may become one of the coefficients, and the second coefficient will be a smaller value. A value of 1 is obtained by a factor of 2.
And that means there is an integer coordinate system.
The coefficients differ in pairs by the same factor, this is the coefficient of the golden section.
You can display an exact representation for the coefficients.
Then the magic of the golden section:
From here a set of laws:
Trivial:
Due to the equality of the ratio of the coefficients:
Squares of coefficients:
Composition:
Based on these properties, you can create a matrix for integer multiplication of vectors:
And all multiplication is reduced to
The vector unit in this system is expressed as {2,0,0,0}. After a simple change of such units, we get {4,0,0,0}. So, the division into two, which was in each formula for the coefficients, is carried out separately, as normalization:
The peculiarity of this coordinate system is that it covers the entire plane with any given accuracy. You can repeat any number of steps, choosing any of the ten directions and still remain in integer coordinates.
But not all combinations of coordinates determine the place reachable from the initial position.
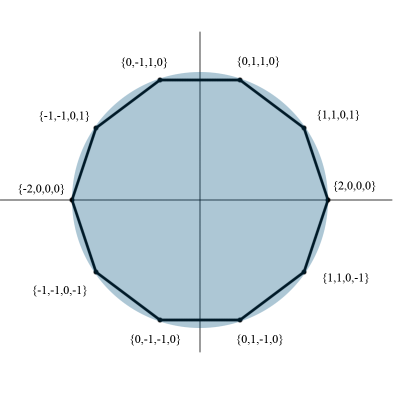
For one step, the coordinates are as follows: {2,0,0,0}, {1,1,0,1}, {0,1,1,0}, {0, -1,1,0}, { -1, -1,0,1}, {-2,0,0,0}, {-1, -1,0, -1}, {0, -1, -1,0}, {0, 1, -1.0}, {1,1,0, -1}. Any combination of these steps is valid.
Together with a single step {2,0,0,0} combinations
{0,1,1,0} - {0,1, -1,0} = {0,0,2,0},
{1,1,0,1} - {1,1,0, -1} = {0,0,0,2},
{1,1,0,1} + {1,1,0, -1} - {2,0,0,0} = {0,2,0,0}
This means that any single coordinate can be shifted by 2, which means that only group parity of coordinates affects reachability. There are four achievable combinations: zero: {0,0,0,0}, from single steps: {1,1,0,1}, {0,1,1,0}, and their combination: {1,0, 1.1}.
As can be seen, the group parity of the abcissal coordinates is uniquely interrelated with the group parity of the ordinate coordinates. This means that the vertical coordinates are divided into four types, the horizontal coordinates are also divided into 4 types, and the coordinate system contains points only with their correct combination.

To approach an arbitrary point, you need to decompose each coordinate into suitable integer factors, taking into account group parity.
In general, there is a coordinate system that combines an integer coordinate value and turns of 36 °. When I brought her out, I was surprised that I did not know about her before. But now about her there is an article on Habré.

The distribution of angles in a diamond in one is 1: 4, 36 °: 144 °, in the other 2: 3, 72 °: 108 °. Diamond angles are multiples of one-tenth of a full turn, 36 °.
Determine the coordinates of the corners of a regular decagon.
| degree | cos | sin |
|---|---|---|
| 0 | one | 0 |
| 36 | 0,809017 | 0.587785 |
| 72 | 0,309017 | 0.951056 |
')

The rest are symmetrical, only the sign changes.
It is immediately noticeable that the cosines of the angles 36 ° and 72 ° differ by 0.5. And this is a very significant fact!
The absolute values of the coordinates are exactly three pieces, both for the abscissa and ordinate coordinates. All three can be represented as two coefficients with integer multipliers.
For the abscissa coordinates, it is simple: among the values are zero, which is represented by zero multipliers. Among the ordinate coordinates, the third — one — is not commensurate with the other two. But, since the difference in coordinates is 0.5, this difference may become one of the coefficients, and the second coefficient will be a smaller value. A value of 1 is obtained by a factor of 2.
| * 36 ° | x | y | ||
| C xa = 0,5 | C xb = 0.309017 | C ya = 0.951056 | C xb = 0,587785 | |
| 0 | 2 | 0 | 0 | 0 |
| one | one | one | 0 | one |
| 2 | 0 | one | one | 0 |
| 3 | 0 | -one | one | 0 |
| four | -one | -one | 0 | one |
| five | -2 | 0 | 0 | 0 |
| 6 | -one | -one | 0 | -one |
| 7 | 0 | -one | -one | 0 |
| eight | 0 | one | -one | 0 |
| 9 | one | one | 0 | -one |
And that means there is an integer coordinate system.

The coefficients differ in pairs by the same factor, this is the coefficient of the golden section.
You can display an exact representation for the coefficients.
Then the magic of the golden section:
From here a set of laws:
Trivial:
Due to the equality of the ratio of the coefficients:
Squares of coefficients:
Composition:
Based on these properties, you can create a matrix for integer multiplication of vectors:
const crd vmul[16] = { { 1, 0, 0, 0}, { 0, 1, 0, 0}, { 0, 0, 1, 0}, { 0, 0, 0, 1}, { 0, 1, 0, 0}, { 1,-1, 0, 0}, { 0, 0, 0, 1}, { 0, 0, 1,-1}, { 0, 0, 1, 0}, { 0, 0, 0, 1}, {-3,-1, 0, 0}, {-1,-2, 0, 0}, { 0, 0, 0, 1}, { 0, 0, 1,-1}, {-1,-2, 0, 0}, {-2, 1, 0, 0} }; And all multiplication is reduced to
int* vm = (int*)vmul; for(int i = 0; i < 4; i++) for(int j = 0; j < 4; j++) for(int k = 0; k < 4; k++) v3[k] += v1[i] * v2[j] * vm[(i * 4 + j) * 4 + k]; The vector unit in this system is expressed as {2,0,0,0}. After a simple change of such units, we get {4,0,0,0}. So, the division into two, which was in each formula for the coefficients, is carried out separately, as normalization:
for(int i = 0; i < 4; i++) v3[i] /= 2; The peculiarity of this coordinate system is that it covers the entire plane with any given accuracy. You can repeat any number of steps, choosing any of the ten directions and still remain in integer coordinates.
But not all combinations of coordinates determine the place reachable from the initial position.
For one step, the coordinates are as follows: {2,0,0,0}, {1,1,0,1}, {0,1,1,0}, {0, -1,1,0}, { -1, -1,0,1}, {-2,0,0,0}, {-1, -1,0, -1}, {0, -1, -1,0}, {0, 1, -1.0}, {1,1,0, -1}. Any combination of these steps is valid.
Together with a single step {2,0,0,0} combinations
{0,1,1,0} - {0,1, -1,0} = {0,0,2,0},
{1,1,0,1} - {1,1,0, -1} = {0,0,0,2},
{1,1,0,1} + {1,1,0, -1} - {2,0,0,0} = {0,2,0,0}
This means that any single coordinate can be shifted by 2, which means that only group parity of coordinates affects reachability. There are four achievable combinations: zero: {0,0,0,0}, from single steps: {1,1,0,1}, {0,1,1,0}, and their combination: {1,0, 1.1}.
As can be seen, the group parity of the abcissal coordinates is uniquely interrelated with the group parity of the ordinate coordinates. This means that the vertical coordinates are divided into four types, the horizontal coordinates are also divided into 4 types, and the coordinate system contains points only with their correct combination.

To approach an arbitrary point, you need to decompose each coordinate into suitable integer factors, taking into account group parity.
In general, there is a coordinate system that combines an integer coordinate value and turns of 36 °. When I brought her out, I was surprised that I did not know about her before. But now about her there is an article on Habré.
Source: https://habr.com/ru/post/342556/
All Articles