Planning tasks and constraint programming
When you have in stock a lot of popular tools like JAVA, Python, Ruby, PHP, C #, C ++ and others, you feel almost omnipotent. The standard approach in the development of taxis. But only until you come across a certain type of tasks.
Think about how to write a program that is optimal ...
• solves a sudoku-type puzzle or the eight queens problem;
• distribute tasks between a specific set of resources;
• calculate the schedule of classes;
• determine the effective route of traffic;
• make a schedule of duty, etc.
')
If programming in constraints and solving complex combinatorial planning problems is not your strongest side, then this article is for you.

Take as an example one of the tasks of scheduling - the calculation of the duty roster. What difficulties can a programmer have when choosing a schedule calculation algorithm? At first glance, everything is very simple. You can use a simple algorithm. Randomly or better consistently evenly distribute duty among employees.
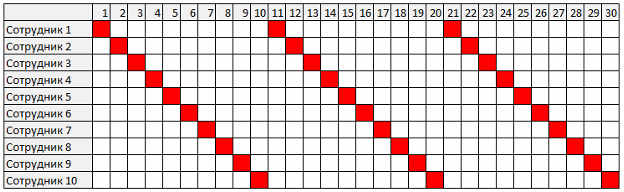
This is the perfect option. However, in real life is much more complicated. Usually there are many additional conditions that must be taken into account. Employees go on vacation or transfer days and, as a result, shifts appear. It becomes even more difficult if you want to take into account the wishes of employees, the duties are divided into several shifts, or the choice of a person depends on the level of his qualifications and so on. At some point, a simple algorithm stops working. You can try to go the other way - to find the optimal solution among the set of all possible combinations. However, there is another problem.
What is the difficulty? Planning tasks are related to the combinatorics mathematics section. Typically, this kind of task is not one, but many solutions and sometimes very large. A simple example. In how many ways can you create a duty schedule for a period of 30 days, when every day one employee out of 10 is on duty? It turns out 10 to 30 degrees (nonillion) ways. If the conditions are similar, but the day is divided into three shifts (one employee per shift), we get in 30 degree options. Finding the best option among such a large number of combinations using the exhaustive search method is beyond the power of even the most powerful computer itself.
Another difficulty: most planning tasks are part of the complex NP-hard combinatorial problems. The bad news is that for NP-hard problems there is no effective universal ( polynomial ) algorithm that allows one to find a provably optimal solution in a reasonable time.
The good news: despite the lack of a magic pill or silver bullet, there is a way out. There are various approaches that allow you to find a near-optimal solution for this type of problem in a reasonable time.
For the convenience of solving a combinatorial problem, it can be represented as a problem of satisfaction of constraints (CPS). A CSP consists of a simple descriptive scheme: a list of variables (variables), each of which is given a set of possible values (domains), and a list of constraints (constraints) that the variables must satisfy. The solution in the CSP is to find all the possible values that the variables can take in accordance with the conditions of the specified constraints.
Simple CSP Example
CSP does not define specific solution algorithms. There are many different approaches. Some of them can be presented as follows ...
Often, specialized CSP solutions are used, for example, a search tree together with a search algorithm with a return .
In the field of planning and scheduling, a constraint programming technology (CP) is appropriate and often used. Computer implementation of algorithms for the effective solution of large combinatorial problems. Unlike the usual form of imperative programming , CP uses declarative . This simplifies the work: it is enough just to describe the problem, all the calculations and the search for values are performed by the solver (Solver), which contains efficient calculation algorithms.
Restriction programming is inextricably linked with the task of satisfying constraints. Therefore, the CSP described earlier as an example is very easy to imagine as a program.
For example, in the MiniZinc language, it will look like this:
After completion of the program, the program will display all valid values of the variables in accordance with the specified restrictions:
For programming in constraints, both separate programming environments with CP support and plug-in libraries in conventional programming languages are used.
Link libraries:
Separate programming environments:
Take as an example the problem of calculating the duty schedule. Imagine it as a CSP model. The conditions of the problem will be obviously simplified and carry only for informational purposes.
Legend
1. Baseline
2. Variables (VARIABLES)
We define a set of variables X as a two-dimensional matrix. The order of variables in each row corresponds to the days of duty for a particular employee.
Domain of valid values for variables:
3. Restrictions (CONSTRAINTS)
Every day only one employee can be the main person on duty.
Every day, only one employee can be a standby officer.
The number of main duties for each employee for the entire time period must be greater than or equal to three.
We define a deterministic finite automaton . We describe the order of distribution of duty. After the main duty the employee takes the standby duty, followed by one or more days of rest. Transitions between the states are indicated: main = 1 — main duty, reserve = 2 — reserve duty, off = 3 — day of rest.
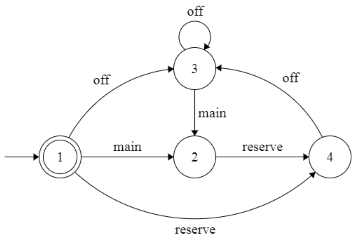
Description of the states of the automaton in the form of a transition table:
And now perhaps the most interesting. Let's write a real program that calculates the duty schedule according to the specified CSP conditions. We will use MiniZinc as a constraint programming environment.
We will rewrite the CSP duty schedule model in the MiniZinc program code, execute the program and solve the problem.
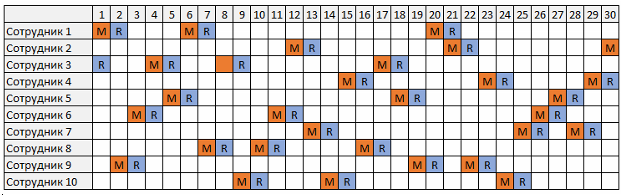
After completion of the program, we obtain one of the possible options for the duty schedule. The sequence of distribution of duty for each employee (horizontal lines), where M (Main) is the main duty, R (Reserve) is the reserve duty, "-" - the employee is not on duty.
Or if it is presented in a more understandable form, then:
If vacation dates are known in advance when an employee should not be on duty, or, conversely, one should fix the duty of a specific employee on a specific date, this can be done through additional restrictions. For example, in order for the fifth employee to be the main duty officer of the first number, and the second employee would not be on duty for the sixth, we set the restriction:
constraint X [5,1] = 1 / \ X [2,6] = 3;
A happy owner of a hammer may have the illusion that the tool is suitable for solving any problems. But the hammer is not universal, and in some cases its advantages are not at all obvious. And there are many such cases. Similarly, in programming, some problems are solved incorrectly or suboptimally, unless specialized approaches are used. Restriction programming is a powerful tool, another paradigm that helps to effectively solve a large number of practical combinatorial problems.
A lot of useful information on constraint programming can be found on the Hakan Kjellerstrand blog , as well as a large number of MiniZinc task examples here or here .
Related Links:
Nurse scheduling problem
Satisfaction of limitations
Constraint programming
MiniZinc Home Page
MiniZinc tutorial
The MiniZinc Challenge
Think about how to write a program that is optimal ...
• solves a sudoku-type puzzle or the eight queens problem;
• distribute tasks between a specific set of resources;
• calculate the schedule of classes;
• determine the effective route of traffic;
• make a schedule of duty, etc.
')
If programming in constraints and solving complex combinatorial planning problems is not your strongest side, then this article is for you.

Take as an example one of the tasks of scheduling - the calculation of the duty roster. What difficulties can a programmer have when choosing a schedule calculation algorithm? At first glance, everything is very simple. You can use a simple algorithm. Randomly or better consistently evenly distribute duty among employees.

This is the perfect option. However, in real life is much more complicated. Usually there are many additional conditions that must be taken into account. Employees go on vacation or transfer days and, as a result, shifts appear. It becomes even more difficult if you want to take into account the wishes of employees, the duties are divided into several shifts, or the choice of a person depends on the level of his qualifications and so on. At some point, a simple algorithm stops working. You can try to go the other way - to find the optimal solution among the set of all possible combinations. However, there is another problem.
By itself, the problem of optimal distribution of attendants with all restrictions is not new. There is already more than 40 years and is known as the Nurse scheduling problem (NSP).
What is the difficulty? Planning tasks are related to the combinatorics mathematics section. Typically, this kind of task is not one, but many solutions and sometimes very large. A simple example. In how many ways can you create a duty schedule for a period of 30 days, when every day one employee out of 10 is on duty? It turns out 10 to 30 degrees (nonillion) ways. If the conditions are similar, but the day is divided into three shifts (one employee per shift), we get in 30 degree options. Finding the best option among such a large number of combinations using the exhaustive search method is beyond the power of even the most powerful computer itself.
Another difficulty: most planning tasks are part of the complex NP-hard combinatorial problems. The bad news is that for NP-hard problems there is no effective universal ( polynomial ) algorithm that allows one to find a provably optimal solution in a reasonable time.
Although theoretically such an algorithm may exist, the question still remains open (see Equality of the classes P and NP ). The price of the question is $ 1,000,000 (see Millennium Problems ).
The good news: despite the lack of a magic pill or silver bullet, there is a way out. There are various approaches that allow you to find a near-optimal solution for this type of problem in a reasonable time.
Combinatorial problem as a problem of satisfying constraints
For the convenience of solving a combinatorial problem, it can be represented as a problem of satisfaction of constraints (CPS). A CSP consists of a simple descriptive scheme: a list of variables (variables), each of which is given a set of possible values (domains), and a list of constraints (constraints) that the variables must satisfy. The solution in the CSP is to find all the possible values that the variables can take in accordance with the conditions of the specified constraints.
Simple CSP Example
- Variables:
- Limitations:
- Decision:
CSP does not define specific solution algorithms. There are many different approaches. Some of them can be presented as follows ...
- Integer programming techniques (Integer programming):
- Gomory algorithm (Cutting-plane method);
- Branch and bound method .
- Algorithms of local search (Local search):
- Algorithm for simulating annealing (Simulated annealing);
- Threshold accepting algorithm;
- Search with bans ( Tabu search );
- Genetic algorithms (Genetic algorithms);
- Min-conflicts algorithm.
- Neural networks.
Often, specialized CSP solutions are used, for example, a search tree together with a search algorithm with a return .
CSP and constraint programming
In the field of planning and scheduling, a constraint programming technology (CP) is appropriate and often used. Computer implementation of algorithms for the effective solution of large combinatorial problems. Unlike the usual form of imperative programming , CP uses declarative . This simplifies the work: it is enough just to describe the problem, all the calculations and the search for values are performed by the solver (Solver), which contains efficient calculation algorithms.
Restriction programming is inextricably linked with the task of satisfying constraints. Therefore, the CSP described earlier as an example is very easy to imagine as a program.
For example, in the MiniZinc language, it will look like this:
% VARIABLES var {1,2,3}: X; var {1,2}: Y; var {1,2,3}: Z; % CONSTRAINTS constraint X != Y; constraint X = Z; constraint Y < Z; % SOLVER solve satisfy; % OUTPUT output ["X=", show(X), " Y=", show(Y), " Z=", show(Z)]; After completion of the program, the program will display all valid values of the variables in accordance with the specified restrictions:
X=2 Y=1 Z=2
----------
X=3 Y=1 Z=3
----------
X=3 Y=2 Z=3
----------
For programming in constraints, both separate programming environments with CP support and plug-in libraries in conventional programming languages are used.
Link libraries:
- Google Optimization Tools (OR-Tools) (C ++, Python, .Net, Java)
- Gecode (C ++, Gecode_Interfaces )
- Chuffed (C ++)
- COIN-OR CBC (C ++)
- OptaPlanner (Java)
- JaCoP (java)
- Choco (java)
- CHIP V5 (C ++)
- Microsoft Solver Foundation (.Net)
Separate programming environments:
- MiniZinc
- IBM ILOG CPLEX
- AIMMS
- ECLiPSe Constraint Programming System
- Babelsberg
- The Mozart Programming System
- HAL
- Common Lisp Screamer
- Curry
- Constraint Handling Rules (CHR)
- The Elf Meta-Language
Duty Schedule in CSP Format
Take as an example the problem of calculating the duty schedule. Imagine it as a CSP model. The conditions of the problem will be obviously simplified and carry only for informational purposes.
Legend
- It is necessary to calculate the duty schedule for 10 people for a period of 30 days.
- Every day there are two employees on duty, one in charge of the main duty officer and the second in standby.
- Each employee for the entire time period, the total number of main duties should be more or exactly three.
- The next day after the main duty, the officer takes over as a standby officer, followed by one or more days of rest.
1. Baseline
- n is the number of days in the billing period (n = 30)
- m - the number of duty (m = 10)
- d - day index (d = 1, ..., n)
- e - employee index (e = 1, ..., m)
2. Variables (VARIABLES)
We define a set of variables X as a two-dimensional matrix. The order of variables in each row corresponds to the days of duty for a particular employee.
Domain of valid values for variables:
3. Restrictions (CONSTRAINTS)
Every day only one employee can be the main person on duty.
Square brackets - designation in Iverson notation
Every day, only one employee can be a standby officer.
The number of main duties for each employee for the entire time period must be greater than or equal to three.
We define a deterministic finite automaton . We describe the order of distribution of duty. After the main duty the employee takes the standby duty, followed by one or more days of rest. Transitions between the states are indicated: main = 1 — main duty, reserve = 2 — reserve duty, off = 3 — day of rest.

Description of the states of the automaton in the form of a transition table:

The task could be formulated in different ways. For example, to present a set of X values in the form of a three-dimensional matrix with a domain of values one and zero (the third dimension for the three types of duties). Or, for each type of duty, define a separate variable.
Practical implementation of duty schedule on MiniZinc
And now perhaps the most interesting. Let's write a real program that calculates the duty schedule according to the specified CSP conditions. We will use MiniZinc as a constraint programming environment.
MiniZinc is a high-level, open source restriction modeling language. Unlike other CP programming environments, it is completely independent of solvers (solver-independent). On MiniZinc, it is easy to build models of different complexity and experiment with them on third-party solvers. The arsenal of the language contains a library with a large number of global constraints ( Global constraints MiniZinc ), and it is also possible to create custom constraints (predicates). This greatly simplifies the modeling of application problems.
Independence from solvers is achieved by translating MiniZinc programs into the lower-level FlatZinc code. FlatZinc through interfaces is supported by a large number of solvers .
MiniZinc is available for use on most platforms (Windows, Mac OS, Linux), and also has a separate IDE .
For a more detailed acquaintance with the MiniZinc language, it is strongly recommended to read the MiniZinc Tutorial manual, where all the features of the language are described in a very clear form and there are many examples.
We will rewrite the CSP duty schedule model in the MiniZinc program code, execute the program and solve the problem.
include "regular.mzn"; %-------------------------------------------------- % 1. INITIAL DATA. %-------------------------------------------------- int: n = 30; int: m = 10; set of int: D = 1..n; set of int: E = 1..m; % array[1..4, 1..3] of int: dfa_states = [|2, 4, 3 |0, 4, 0 |2, 0, 3 |0, 0, 3 |]; %------------------------------------------------- % 2. VARIABLES. %------------------------------------------------- array[E, D] of var 1..3: X; %------------------------------------------------- % 3. CONSTRAINTS. %------------------------------------------------- % 3.1 % 3.2 % /\ constraint forall(d in D)( sum(e in E)( bool2int( X[e, d] = 1 )) = 1 /\ sum(e in E)( bool2int( X[e, d] = 2 )) = 1 ); % 3.3 , constraint forall(e in E)( sum(d in D)( bool2int( X[e, d] = 1 )) >= 3 /\ regular( [X[e, d] | d in D], 4, 3, dfa_states, 1, 1..4 ) % regular - , (dfa_states) ); %------------------------------------------------- % SOLVE %------------------------------------------------- solve satisfy; %------------------------------------------------- % OUTPUT %------------------------------------------------- array[1..3] of string: rest_view = ["M", "R", "-"]; output [ rest_view[fix(X[e, d])] ++ " " ++ if d = n then "\n" else "" endif | e in E, d in D ]; After completion of the program, we obtain one of the possible options for the duty schedule. The sequence of distribution of duty for each employee (horizontal lines), where M (Main) is the main duty, R (Reserve) is the reserve duty, "-" - the employee is not on duty.
MR - - - - - - MR - - - - MR - - - - - - - - - - - - - -
R - - - - MR - - - MR - - - - - - - - - MR - - - - - - -
- - - - - - - MR - - - - - - MR - - - - - - - MR - - - -
- - - - - - MR - - - - - - - - MR - - - - - - - - MR - -
- MR - - - - - - - - - - - - - - - - - MR - MR - - - - -
- - MR - - - - - MR - - - - - - - - - - - MR - - - - - -
- - - - - - - - - - - - MR - - - - - MR - - - - - - MR -
- - - - MR - - - - - MR - - - - - - - - - - - - - - - MR
- - - - - - - - - - - - - MR - - - MR - - - - - - - - - M
- - - MR - - - - - - - - - - - - MR - - - - - - MR - - -
Or if it is presented in a more understandable form, then:

If vacation dates are known in advance when an employee should not be on duty, or, conversely, one should fix the duty of a specific employee on a specific date, this can be done through additional restrictions. For example, in order for the fifth employee to be the main duty officer of the first number, and the second employee would not be on duty for the sixth, we set the restriction:
constraint X [5,1] = 1 / \ X [2,6] = 3;
A slightly more complicated version of the program (Hakan Kjellerstrand) can be found here.
Conclusion
A happy owner of a hammer may have the illusion that the tool is suitable for solving any problems. But the hammer is not universal, and in some cases its advantages are not at all obvious. And there are many such cases. Similarly, in programming, some problems are solved incorrectly or suboptimally, unless specialized approaches are used. Restriction programming is a powerful tool, another paradigm that helps to effectively solve a large number of practical combinatorial problems.
A lot of useful information on constraint programming can be found on the Hakan Kjellerstrand blog , as well as a large number of MiniZinc task examples here or here .
Related Links:
Nurse scheduling problem
Satisfaction of limitations
Constraint programming
MiniZinc Home Page
MiniZinc tutorial
The MiniZinc Challenge
Source: https://habr.com/ru/post/342550/
All Articles