Brilliance and misery of Artificial Intelligence
On the example of a simple task with a simple neural network. Inspired by this article and the network is taken without changes. Just executing the code was uninteresting and an inquiring mind decided to make changes to the object of recognition. Namely, you need to take and mix the points at 28x28 and see.
Here is the code from the article with some changes and please pay special attention to the “permutations” block - there we will introduce and satisfy our curiosity.
Read the original pictures (What kind of pictures and why - please read the original article)
And they chose randomly 10 pieces from Train and Test for display. Pictures are like pictures, if you don’t change anything in them (perm = np.arange (28 * 28)) the network gives 98% or more. Fine.
You can check it yourself.
')
But now randomly shuffle pictures. Accidentally, it is accidental, but all the pictures are interfered equally.
We look at the pictures and launch the network.
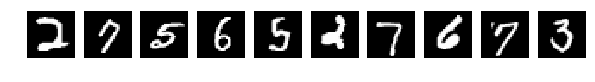
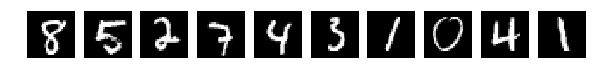
The original, randomly selected by 10 pictures, and now after mixing the same.
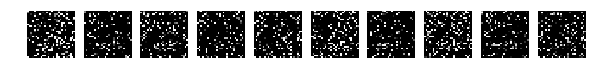
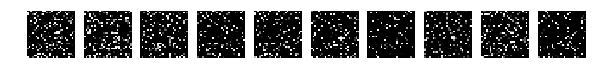
Let me remind you that all the pictures were mixed equally.
But then oh! mystic, the network easily copes with such pictures and I get [0.082131341451834983, 0.98219999999999996].
No one will ever cope with such a task in such mixed pictures. This shine !!! This is phenomenal compared to man. Looking for a big bear and archer need thousands of years.
But the inquisitive mind does not stop at this and is now trying to shake up. More precisely apply another code:
Not points are intermixed, but point values. You can mix it again randomly, but the main thing is the same all over the pictures, but you can choose one very widely known mixing in narrow circles:
And the result of the network (the same code without changes) immediately alerted:
[1.0329392189979554, 0.64970000000000006]
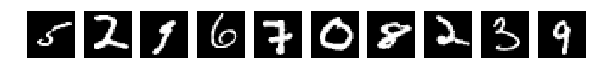
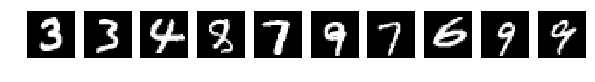
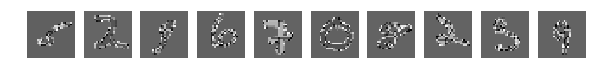

With an eye you can easily understand where the numbers are, but the result of the network’s work is depressing. Agitation significantly worsened the result.
And finally, a spoon of tar.
If a
it is all very bad.
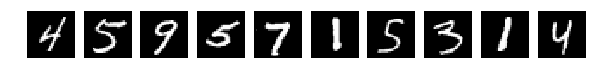
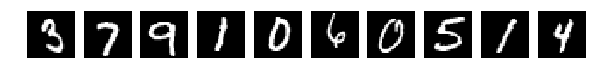
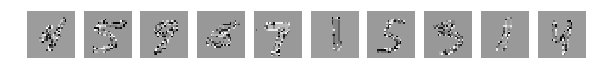
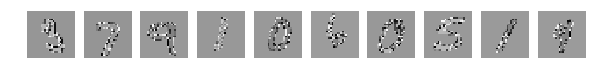
With my eyes you can see everything, but the network gives out
[2.301039520263672, 0.1135]
Conclusion: “Stir, but do not stir.”
Ps. The article leaves a sense of incompleteness. I had to write
continuation about monsters and blondes
Here is the code from the article with some changes and please pay special attention to the “permutations” block - there we will introduce and satisfy our curiosity.
from keras.datasets import mnist from keras.models import Model from keras.layers import Input, Dense from keras.utils import np_utils import numpy as np %matplotlib inline import matplotlib.pyplot as plt batch_size = 128 num_epochs = 16 hidden_size_1 = 512 hidden_size_2 = 512 height, width, depth = 28, 28, 1 # MNIST images are 28x28 and greyscale num_classes = 10 # there are 10 classes (1 per digit) (X_train, y_train), (X_test, y_test) = mnist.load_data() # fetch MNIST data num_train, width, depth = X_train.shape num_test = X_test.shape[0] num_classes = np.unique(y_train).shape[0] # there are 10 image classes #Visualizing I_train = list() I_test = list() fig, axes = plt.subplots(1,10,figsize=(10,10)) for k in range(10): i = np.random.choice(range(len(X_train))) I_train.append(i) axes[k].set_axis_off() axes[k].imshow(X_train[i:i+1][0], cmap='gray') fig, axes = plt.subplots(1,10,figsize=(10,10)) for k in range(10): i = np.random.choice(range(len(X_test))) I_test.append(i) axes[k].set_axis_off() axes[k].imshow(X_test[i:i+1][0], cmap='gray') X_train = X_train.reshape(num_train, height * width) X_test = X_test.reshape(num_test, height * width) XX_test = np.copy(X_test) XX_train = np.copy(X_train) Read the original pictures (What kind of pictures and why - please read the original article)
And they chose randomly 10 pieces from Train and Test for display. Pictures are like pictures, if you don’t change anything in them (perm = np.arange (28 * 28)) the network gives 98% or more. Fine.
You can check it yourself.
')
But now randomly shuffle pictures. Accidentally, it is accidental, but all the pictures are interfered equally.
# perm = np.random.permutation((28*28)) # for j in xrange(X_test.shape[1]): for i in xrange(X_test.shape[0]): X_test[i][j] = XX_test[i][perm[j]] for i in xrange(X_train.shape[0]): X_train[i][j] = XX_train[i][perm[j]] # We look at the pictures and launch the network.
X_train = X_train.reshape(num_train, height, width) X_test = X_test.reshape(num_test, height, width) #Visualizing fig, axes = plt.subplots(1,10,figsize=(10,10)) for k in range(10): i = I_train[k] axes[k].set_axis_off() axes[k].imshow(X_train[i:i+1][0], cmap='gray') fig, axes = plt.subplots(1,10,figsize=(10,10)) for k in range(10): i = I_test[k] axes[k].set_axis_off() axes[k].imshow(X_test[i:i+1][0], cmap='gray') X_train = X_train.reshape(num_train, height * width) # Flatten data to 1D X_test = X_test.reshape(num_test, height * width) # Flatten data to 1D X_train = X_train.astype('float32') X_test = X_test.astype('float32') X_train /= np.max(X_train) # Normalise data to [0, 1] range X_test /= np.max(X_test) # Normalise data to [0, 1] range Y_train = np_utils.to_categorical(y_train, num_classes) # One-hot encode the labels Y_test = np_utils.to_categorical(y_test, num_classes) # One-hot encode the labels inp = Input(shape=(height * width,)) # Our input is a 1D vector of size 784 hidden_1 = Dense(hidden_size_1, activation='relu')(inp) # First hidden ReLU layer hidden_2 = Dense(hidden_size_2, activation='relu')(hidden_1) # Second hidden ReLU layer out = Dense(num_classes, activation='softmax')(hidden_2) # Output softmax layer model = Model(input=inp, output=out) # To define a model, just specify its input and output layers model.compile(loss='categorical_crossentropy', # using the cross-entropy loss function optimizer='adam', # using the Adam optimiser metrics=['accuracy']) # reporting the accuracy model.fit(X_train, Y_train, # Train the model using the training set... batch_size=batch_size, nb_epoch=num_epochs, verbose=1, validation_split=0.1) # ...holding out 10% of the data for validation model.evaluate(X_test, Y_test, verbose=1) # Evaluate the trained model on the test set! 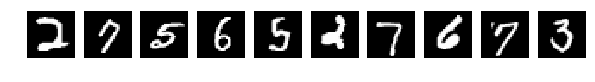
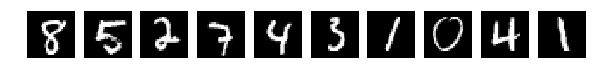
The original, randomly selected by 10 pictures, and now after mixing the same.
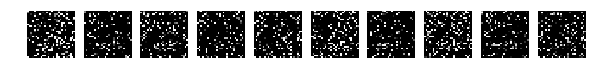
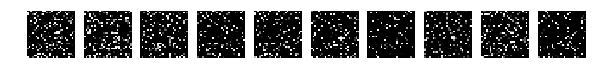
Let me remind you that all the pictures were mixed equally.
But then oh! mystic, the network easily copes with such pictures and I get [0.082131341451834983, 0.98219999999999996].
No one will ever cope with such a task in such mixed pictures. This shine !!! This is phenomenal compared to man. Looking for a big bear and archer need thousands of years.
But the inquisitive mind does not stop at this and is now trying to shake up. More precisely apply another code:
for j in xrange(X_test.shape[1]): for i in xrange(X_test.shape[0]): X_test[i][j] = perm[XX_test[i][j]] for i in xrange(X_train.shape[0]): X_train[i][j] = perm[XX_train[i][j]] Not points are intermixed, but point values. You can mix it again randomly, but the main thing is the same all over the pictures, but you can choose one very widely known mixing in narrow circles:
perm = np.array([ 0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76, 0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0, 0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15, 0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75, 0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84, 0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf, 0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8, 0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2, 0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73, 0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb, 0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79, 0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08, 0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a, 0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e, 0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf, 0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16]) And the result of the network (the same code without changes) immediately alerted:
[1.0329392189979554, 0.64970000000000006]
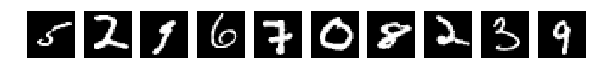
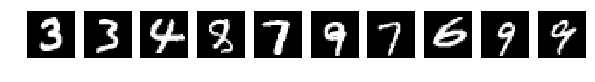
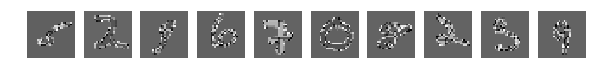

With an eye you can easily understand where the numbers are, but the result of the network’s work is depressing. Agitation significantly worsened the result.
And finally, a spoon of tar.
If a
perm = np.array([ 153, 17, 7, 148, 191, 15, 73, 109, 180, 129, 2, 218, 122, 151, 227, 167, 40, 248, 66, 212, 197, 101, 211, 139, 234, 133, 168, 174, 53, 207, 219, 37, 246, 194, 239, 255, 107, 90, 22, 44, 215, 84, 102, 201, 61, 176, 72, 125, 56, 99, 156, 161, 226, 6, 238, 52, 27, 50, 216, 231, 71, 5, 25, 34, 62, 29, 166, 253, 220, 3, 24, 225, 130, 196, 113, 86, 150, 209, 65, 195, 1, 200, 41, 81, 69, 163, 33, 147, 230, 202, 232, 112, 241, 137, 47, 187, 203, 175, 229, 39, 160, 186, 152, 222, 14, 85, 21, 77, 210, 108, 193, 250, 54, 45, 92, 141, 94, 208, 110, 192, 228, 115, 91, 143, 26, 88, 96, 170, 78, 87, 132, 172, 247, 178, 205, 165, 177, 144, 83, 49, 11, 67, 82, 134, 245, 100, 18, 48, 136, 213, 105, 162, 199, 103, 252, 214, 158, 189, 149, 95, 164, 111, 233, 181, 142, 249, 9, 236, 38, 173, 243, 57, 28, 128, 55, 32, 116, 59, 145, 97, 35, 106, 43, 206, 198, 60, 135, 74, 23, 76, 251, 120, 240, 75, 20, 169, 179, 121, 80, 217, 123, 235, 126, 114, 16, 155, 146, 119, 19, 8, 51, 98, 42, 185, 127, 93, 190, 104, 224, 171, 244, 124, 89, 68, 0, 4, 117, 182, 70, 64, 159, 157, 242, 188, 10, 30, 36, 58, 138, 118, 204, 184, 221, 13, 254, 31, 12, 140, 63, 223, 79, 46, 154, 183, 131, 237]) it is all very bad.
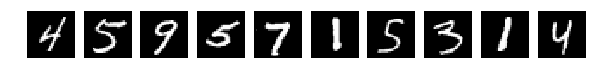
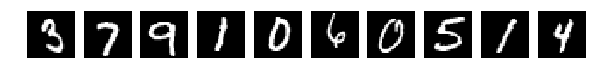
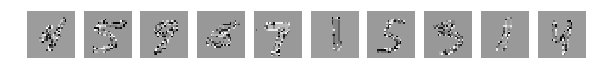
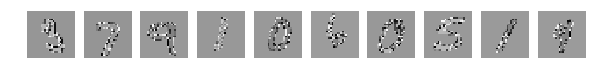
With my eyes you can see everything, but the network gives out
[2.301039520263672, 0.1135]
Conclusion: “Stir, but do not stir.”
Ps. The article leaves a sense of incompleteness. I had to write
continuation about monsters and blondes
Source: https://habr.com/ru/post/342176/
All Articles