Simulator cars Breitenberg
Just wanted to write a simulator of Breitenberg machines. The roots of this thing grow from the ideas of building unpretentious robots, but it is also interesting from the point of view of the development of complex systems.

So what is this?
(Be careful, there are a lot of pictures and animations in the article!)
The Breitenberg typewriter is an automatic machine, on the simplest logic of the minimum number of elements, which, however, demonstrates complex behavior that an external observer can take as reasonable (a simple one looks like a complex, "ponty" of robots).
They are described in 6 types, based on some construction called a neurode . A neurode can receive a braking or accelerating signal that affects the number of pulses at the output. A neural network of such neurodes (even the simplest: 2-8 elements) can create several basic behaviors. The principle of operation is as follows:
')
Sensors (react to light) -> network of neurodes -> actuators (motors)
The first type of behavior is the simplest - when there are no neurodes and the sensor signal goes directly to the motor. Then the left eye turns the left motor the stronger, the more illuminated, and the same with the right one. Such a system will "run away" from the light.
If you cross the conductors (left eye to the right motor and vice versa), we get a light-loving robot, it will go, accelerating, to the light bulb. About other types in more detail as they are modeled.
It was supposed (Breitenberg) to put a swarm of such 6 typewriters into a room with light bulbs, and then the observer (hypothetical robot-psychologist) would see complex behavior in their movements. See whether such complexity you - see. The article will have many gifs with simulations =)
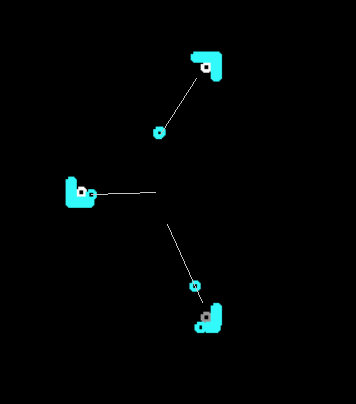
Pozhayluy immediately show a room with a few cars
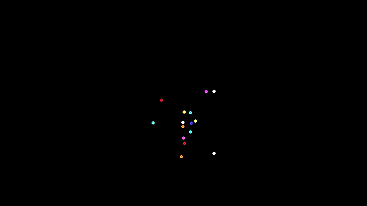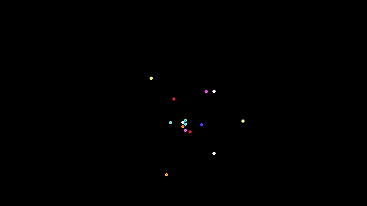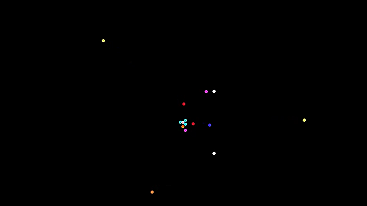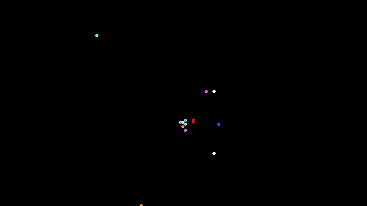
White circles - light bulbs. Colored - automatic machines of different types.
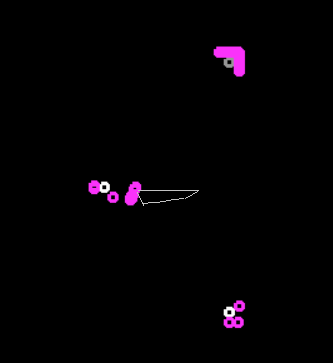
Sometimes a demonstration with the trajectory of each machine gun is more beautiful:
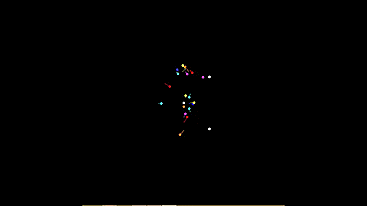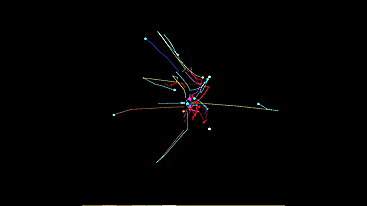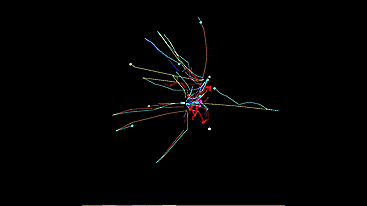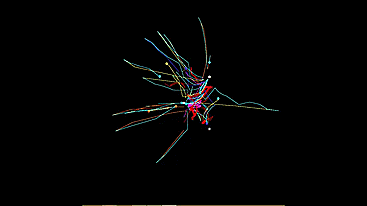
So let's get started . I was the first to implement the light-loving type. There is no need to model the whole system. At first it seemed to me that I could simply divide the power of the light sources by the square of the distance to them, fold the vector and transmit to the machine the resulting vector “direction to the light” as a motion vector. But it turns out quite differently.
Firstly, in the Breitenberg system, the typewriter has two light-sensitive elements. If they are implemented as directional sensors, then they look forward, and if they are undirected, they should not distinguish between forward and backward directions. So I took a plane perpendicular to the motion vector, and reflected “direction to the light” if it pointed back. It turned out such ears, which do not distinguish where the sound came from - in front or behind, but only to the right or left, and what kind of power.
Secondly, the set on wheels cannot move perpendicularly to the side, it has a maximum angle of rotation (per unit of distance traveled), maximum speed and inertia. I added all this by cutting off the angle of the vector of motion relative to the direction vector of the automaton to a certain maximum, cutting it modulo it, and having previously vectorially added them: V_new = Inertia * V_old + (1 - Inertia) * LightDir.
Result:

As a result, features became noticeable - for example, it can be seen that cars passing exactly in the middle between two light bulbs continue to move. Everything is good, we can create a new type based on this.
Now there will be a fear of the light. To do this, you need to do everything too, but reflect the motion vector relative to the current orientation of the machine (not a reflection relative to its coordinate! Otherwise, you will again get a physically unreal apparatus).
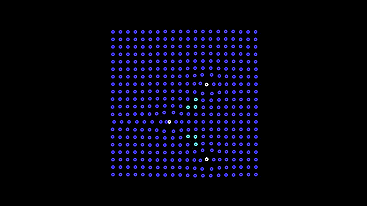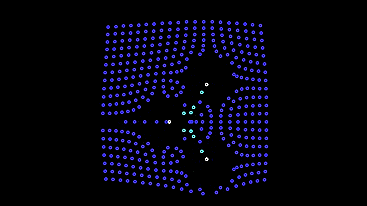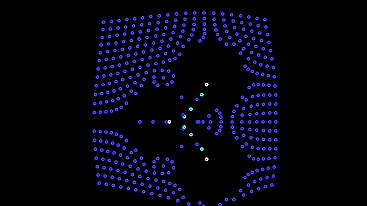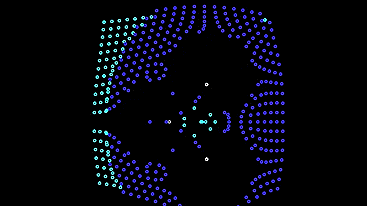
The only negative is that such automata escape from the screen and leave behind an empty field. We put them a protective mechanism against runaway - in low light, they will change their behavior to the first model until they return to the light bulbs.
Now let's set up cars with a couple of neurodes. The first will repeat the model of the light-loving machine, but with embedded neurods on the lines. From the sensor, a braking signal will go to the neurode, and from the neurode, the signal will go to the motor. Now the more we light on the sensor, the less signals to the motor - the slower the car goes. Such a system will have the wiring as the first model, but behave more like the second - to run away from the light. But if the speed of the first one decreases with distance from the source, then this will be the opposite: it will accelerate. Correct the code to calculate the motion vector modulus accordingly and voila:

When I made this machine for the first time it seemed to me that it works correctly, but something was wrong ... This is the first version where I mixed up some kind of sign.

It’s more beautiful to watch them in the track recording mode - they draw something like an eye.

Now the next machine. Again we cross wires, but with neurodes on them (in the code - we remove the last reflection of the vector):
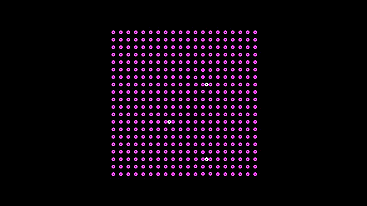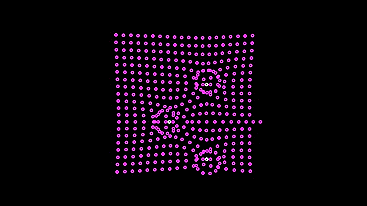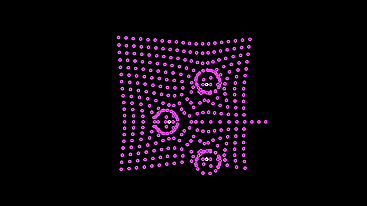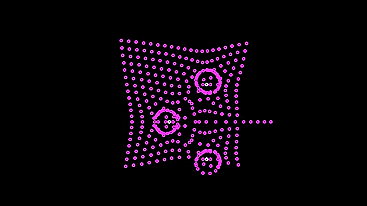
This machine is wiser, it does not break to the light, at the risk of breaking a light bulb (and it would be so in a real model), but stops at a distance when enough light strikes the sensors so that the braking signal completely stops generating signals for the motor.
Number five. Machine with a complex system of neurodes. For a description, you can visit this article , but for now I'll tell you how this is done in simple ways - a barrier in the amount of light is added, and the sign in the reflection operation changes depending on whether the light level is lower than the threshold value, or lower. A real machine should run away like a third when there is little light, and go into the light like a fourth when there is a lot of it. Somewhere there will also be an inner circle, where it will stop altogether - I chose the coefficients for a long time, I often changed them, but I did not achieve a beautiful runaway from the “light edge from the fire”. Anyway, the inner circle of the stop should be wide enough (to occupy more than half of the area) - this is due to the realization of the quadratic light attenuation with increasing distance, so physics is to blame, not me =)

And the last one . This one should change its models according to the opposite principle - to reach for the light when it is not enough, and to run away when there is a lot. Azimov admirers will immediately understand that such a machine will constantly run in a circle on an equipotential line (lines of a constant level of illumination). And if we continue the direct “sensorless” model that I have used so far, the machine will simply reach this line and stop. In the real world, her running in a circle will be due to the fact that one of the eyes is inside the circle, and the other outside, and the internal neurogenic structure will create a new case for the movement algorithm - will make it move perpendicular to the direction of light. In order to simulate this type of automaton, I had to add a real description of two sensors, and in order for one of them to have a value of illumination at some moments below the threshold, when on the other, it was necessary to place them at some distance. The physical distance between sensors is called parallax (for example, between a person’s eyes, or two telescopes in one system). Here is the machine after my dopilov (eyes on gui did not draw).

Changing the parallax causes a change in accuracy

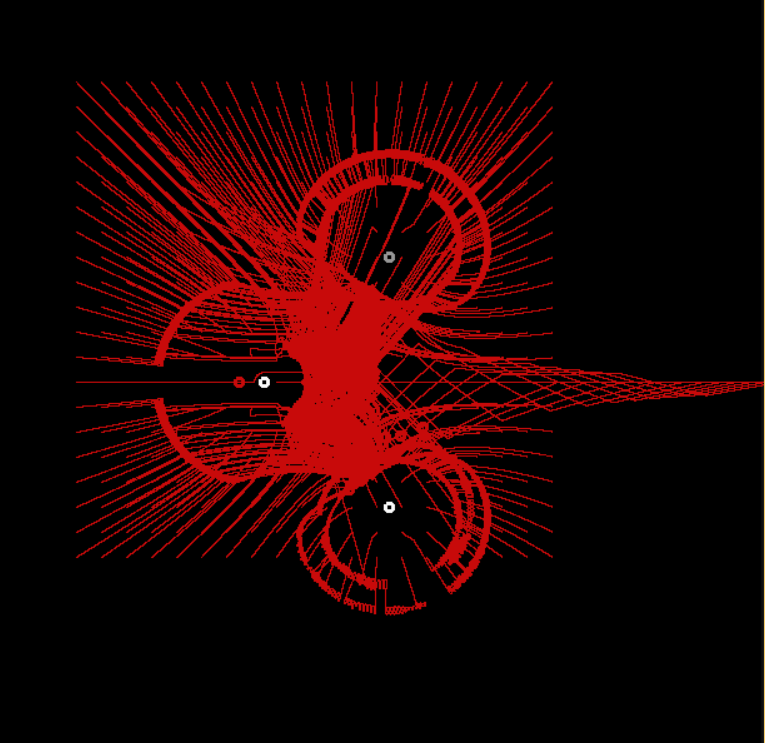
For some values, the automaton moves almost in even arcs, while for others, it moves along wavy paths, constantly approaching and then moving away. Similar behavior for robots in a race on the line.
Now let's throw a family of different types of automata on the field.

The first version at the beginning of the article seemed to me somewhat boring, so I first made some light bulbs to go out and light from time to time ... And then I did a mixing algorithm , which once in a while changed the type of machine to some other one, so so that it goes through "all incarnations":

Without all this, you can look at the grid of all types in one field.

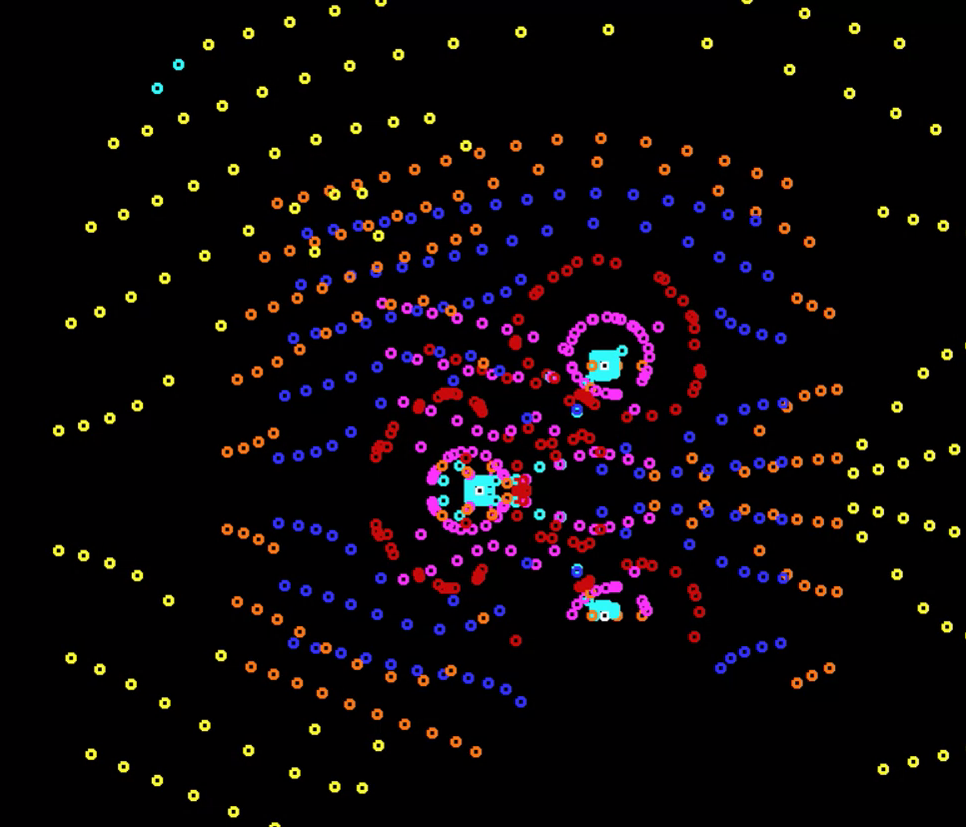
After that, I thought about the machines having a physical size (so that they would not pass through each other), but calculating collisions is a difficult task for a computer, especially with such a large number of participants, so I just took a couple of shots and turned off the mode

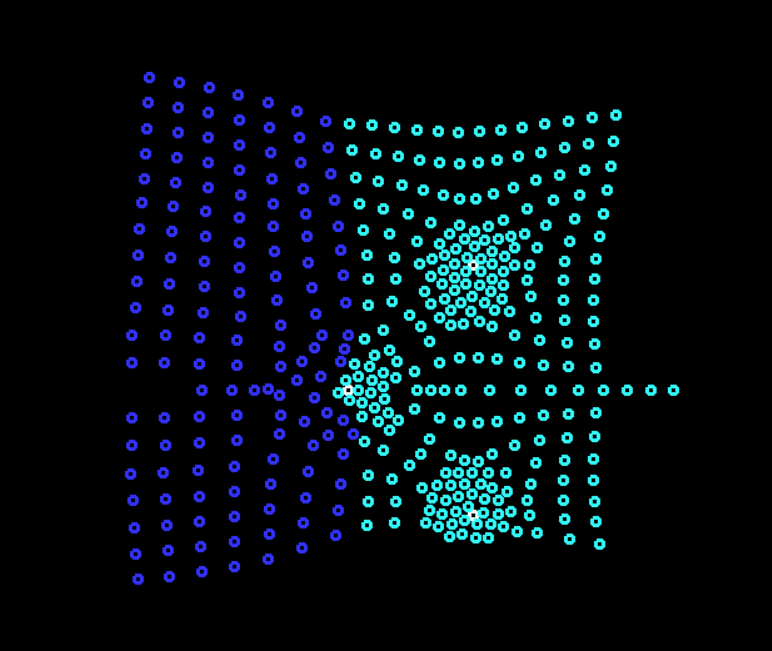
In principle, it was all the same, only the machines pushed around their asymptotic trajectories, and were not exactly on them, that's all. Let's return to the world without collisions)
Consider now the system on a long exposure - what does it want?
The switching mode of the light bulbs does not allow the system to remain a static picture, but the light fans have tried very hard - they are hooked to their lamps and do not have time to run away from them during the period when they are turned off.
Their wiser version is in time, and as a result there is a flock that moves along a cyclic path between the three lamps.
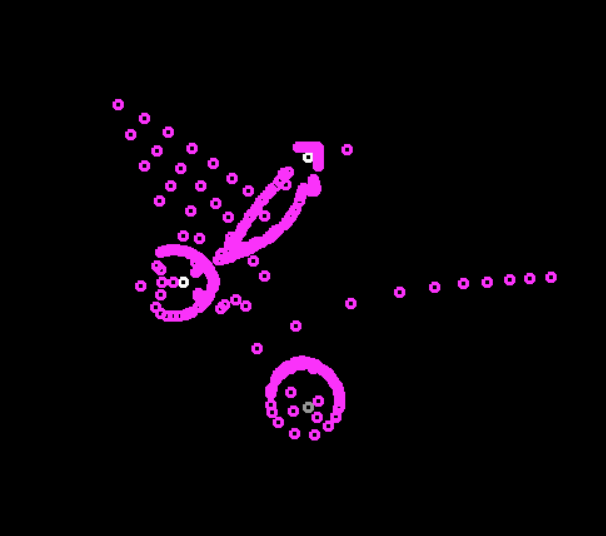
Photoplastic work differently. Since the protection system returns them at the same speed as their removal rate - at each level, they form an even noise, about half of the machines are slowly removed, the other half returns in protection mode.

With their version pumped by neurodes, the situation is different - they quickly fly away, but slowly gather back. I expected that they will eventually form an even narrowing circle, but no. They retain asymmetrical shape, and sometimes give beautiful pictures

Sometimes they look like the same chaos:

The changing machine most often behaves the same way. But in the end, they stumble into very small groups that travel quite a lot from the light bulb and to the light bulb along such rails.
In addition to several machines that caught "their own wave" and spinning on the right side of the room. I waited for them to join one of the three clans, but after 2 hours of simulation this did not happen, it seems that this is the case of strange dynamically stable trajectories, like that asteroid that flies around the gravitational well of the earth, then to the right or to the left.
Cyclic automatons showed a telephone receiver (or a smiling face?), Lumped together, and began to turn and unfold the tentacles in turns to the lamps currently in operation.
Rozhitsa
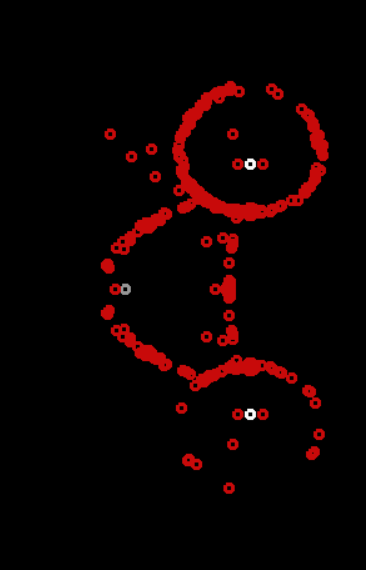
Stable mode

In the meantime, while the long-running simulations were going, I thought about other options and added three more non-standard types . They are guided not by light, but by other automata.
The first of them is waiting for automata to appear in the neighborhood, and is trying to follow the nearest one. The rest of the time it is worth and sad.
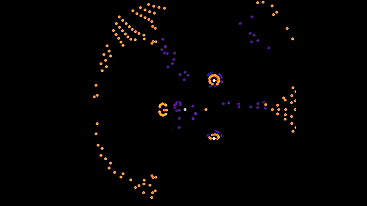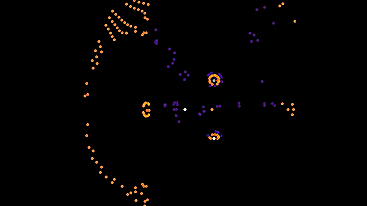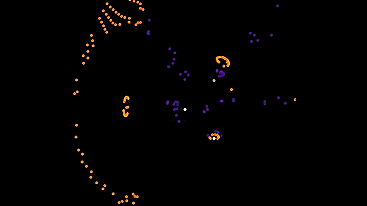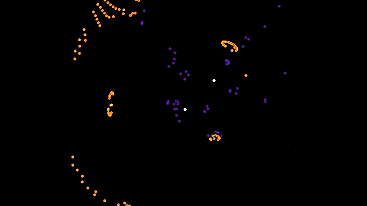
You can call them dogs, because they need owners. I put them on the field with the 5th type, otherwise they would all just stand.
Another type - averages the coordinates of many automata and runs into the crowd - "extrovert."

His antipode is an introvert who tries to keep his distance.

At the beginning, the grid has a translational symmetry and the central automata have no place to go - in any direction they would approach the neighbors, so they wait for the extreme ones to scatter. It looks interesting in the track mode - a shaggy IC is obtained.
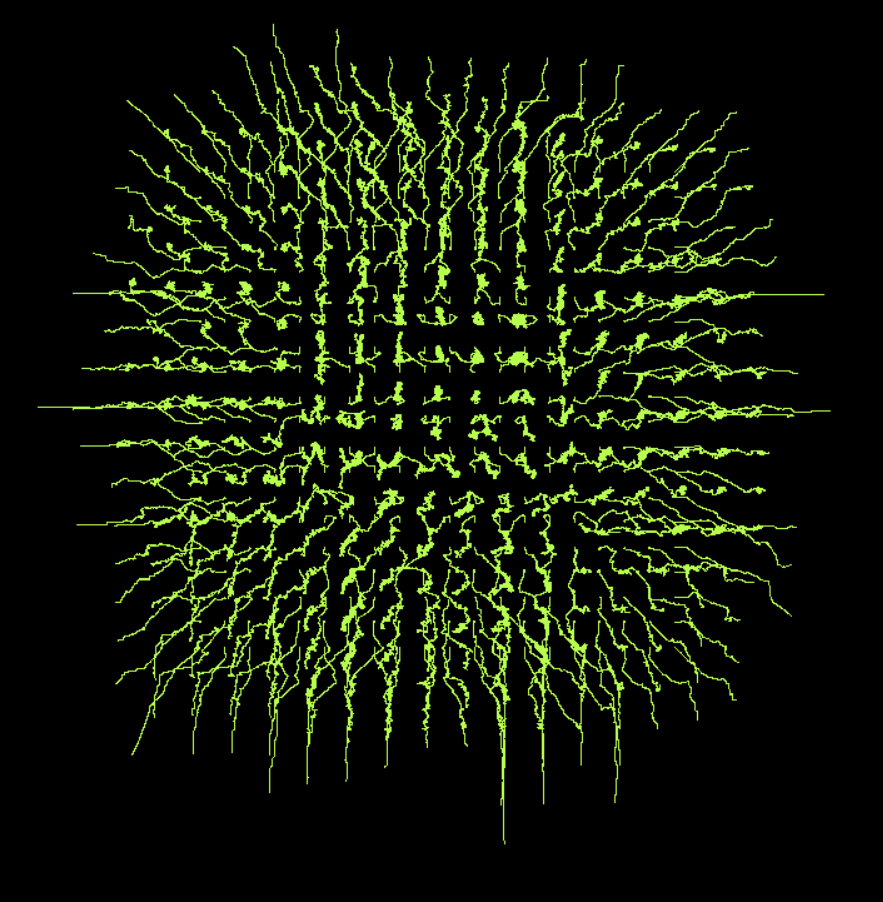
Now put all 9 types (including new ones) and look at the grid. (type mixing included)
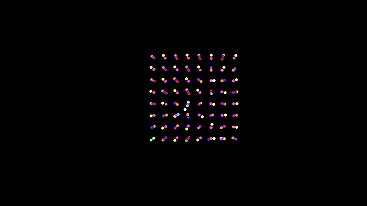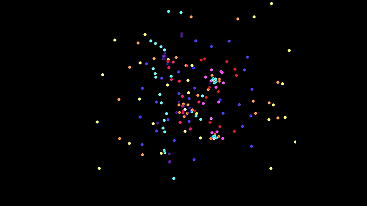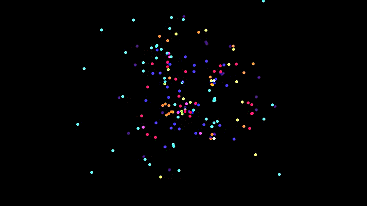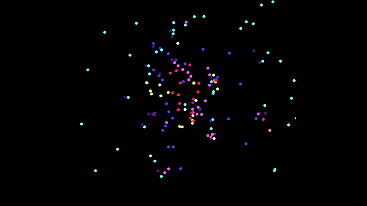
And in the track mode, they draw a dandelion

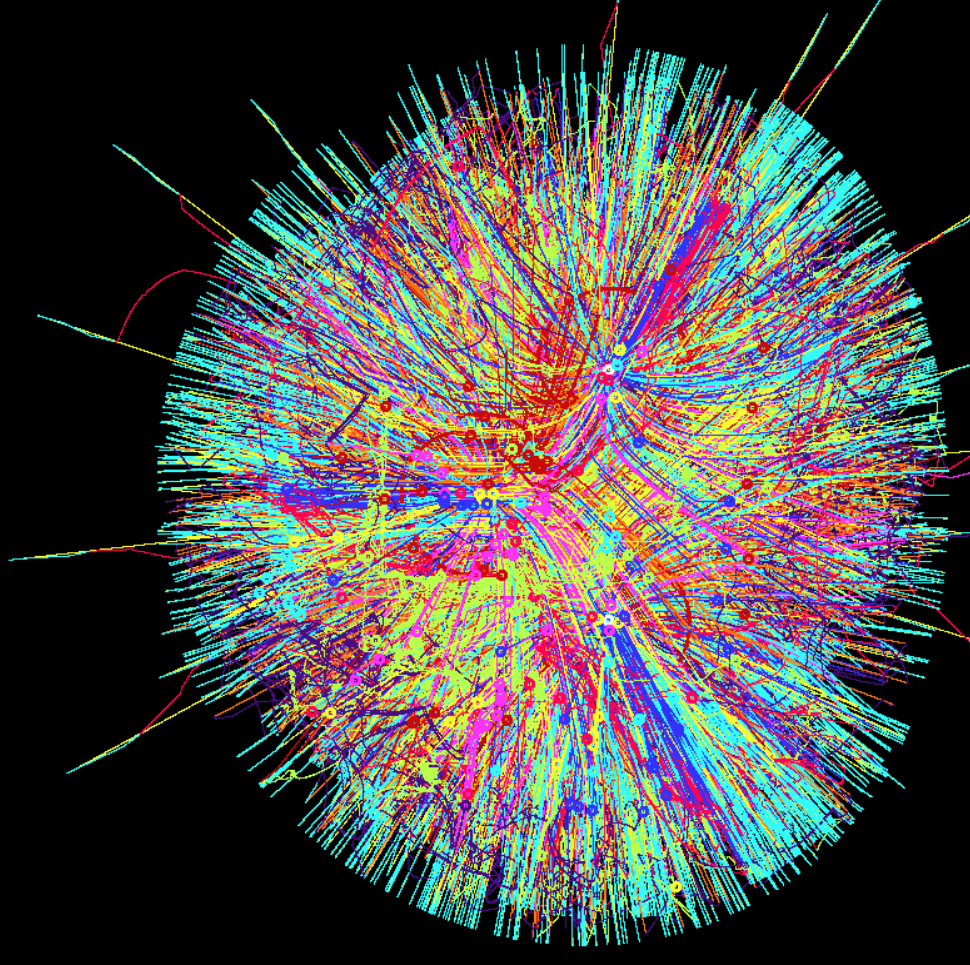
In the center I placed a light source with a negative power value. I don’t know what I expected, but the anti-light though lures the usually fleeing automata, but their behavior does not become similar to the “crossed” analogues of light lovers, but it turns out something third, more complex.
More dandelions that turned out.




So, too, it turns dandelion. I became interested when I saw the drawing of the “cobweb” in the corner of one of the simulations - the fugitives fled into the distance with rays, and the dogs did not have time for them, and moved from one to the other with half-arches. I thought that if you do it so massively, you get a cobweb, as it is always painted. Therefore, I threw into the room only these two types of machine guns - but something went wrong. In any configuration, the system is unstable and the dogs collapse in some direction, as a result, just another dandelion comes out - and no cobwebs.

Added another lamp.


But ... Um ... Porcupine?

In general, the behavior, as for my taste, is really quite complicated. But let's move on. Let's try to show nonlinearity . A runaway version works well for this. The divergence from the sphere (which is an equipotential in illumination surface around the bulb) almost guarantees the appearance of deterministic chaos.
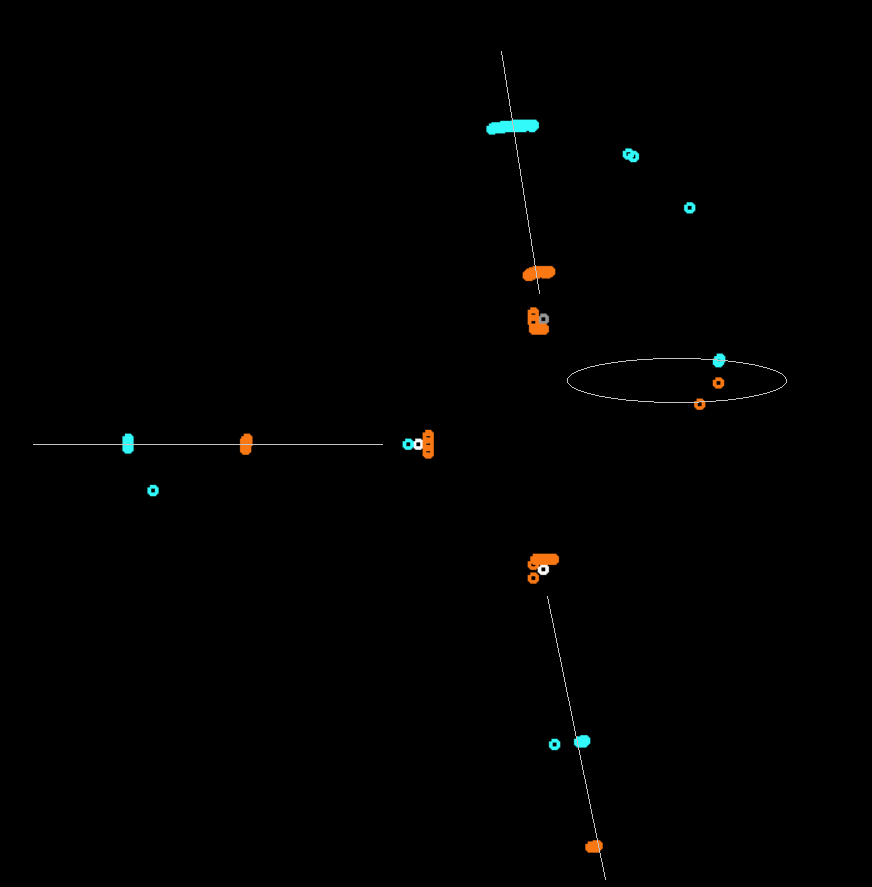
Let's run the same grid, but very small in size - so that the initial conditions for the machines differ only slightly (automata leave almost from one point), and see how the system develops and what it will show us.
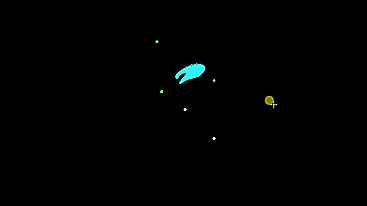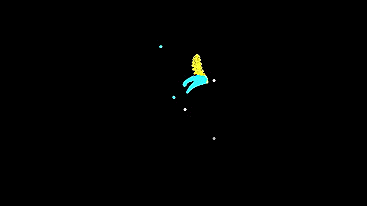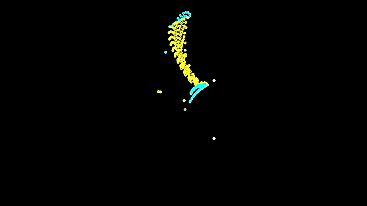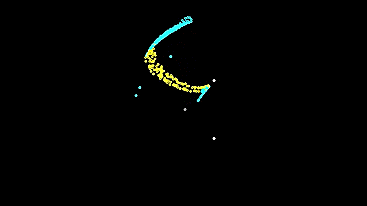
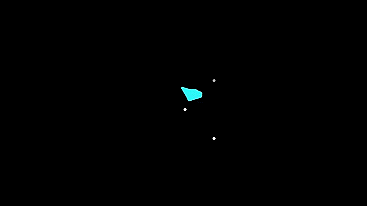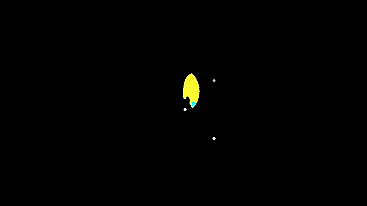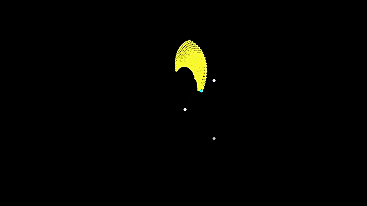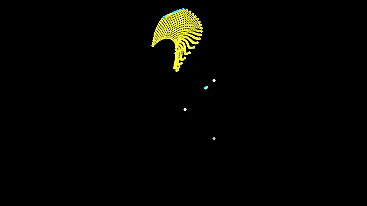
Now let's run the same small grid, but with different types of machines and enabled type mixing.

Such interesting pictures are obtained ... For a change, you can change the visualization model , say, connect all the cars with lines (as if they would pull one long string). So it is more convenient to observe exactly how the algorithm crumples the initially flat grid of machines, and where it sends its different parts - how they migrate around their world.
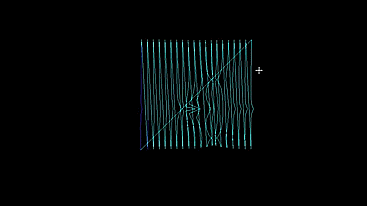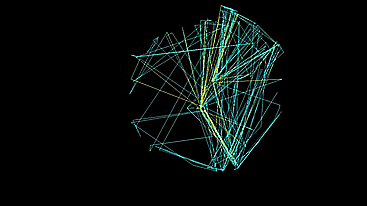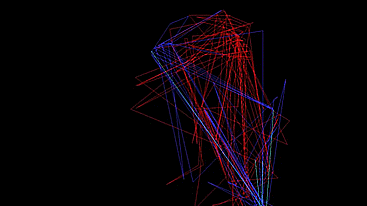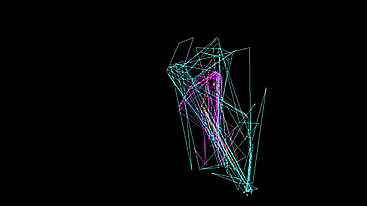
Get stuck like the one in the media player.
Sometimes interesting shapes appear.


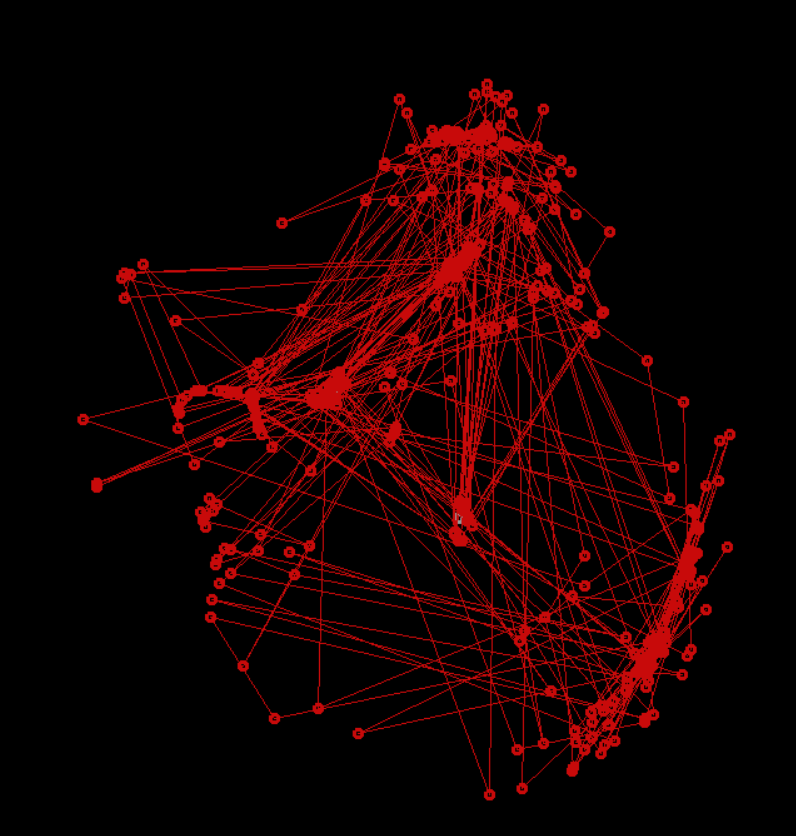

In general , such a simulator. Feel free to offer your ideas and suggestions in the comments, what else can you add, or what experiment to put. Personally, I think the resulting piece is a convenient demonstration for the theory of nonlinear systems - in it you can look for assymptotics, divergences, curious patterns, showing the complexity of simple systems ... People can use the concept both in automation and beginners in building BEAM robots - to understand the essence, and in general - see color pictures.
All good, robotopsihologi. It's all.

So what is this?
(Be careful, there are a lot of pictures and animations in the article!)
The Breitenberg typewriter is an automatic machine, on the simplest logic of the minimum number of elements, which, however, demonstrates complex behavior that an external observer can take as reasonable (a simple one looks like a complex, "ponty" of robots).
They are described in 6 types, based on some construction called a neurode . A neurode can receive a braking or accelerating signal that affects the number of pulses at the output. A neural network of such neurodes (even the simplest: 2-8 elements) can create several basic behaviors. The principle of operation is as follows:
')
Sensors (react to light) -> network of neurodes -> actuators (motors)
The first type of behavior is the simplest - when there are no neurodes and the sensor signal goes directly to the motor. Then the left eye turns the left motor the stronger, the more illuminated, and the same with the right one. Such a system will "run away" from the light.
If you cross the conductors (left eye to the right motor and vice versa), we get a light-loving robot, it will go, accelerating, to the light bulb. About other types in more detail as they are modeled.
It was supposed (Breitenberg) to put a swarm of such 6 typewriters into a room with light bulbs, and then the observer (hypothetical robot-psychologist) would see complex behavior in their movements. See whether such complexity you - see. The article will have many gifs with simulations =)
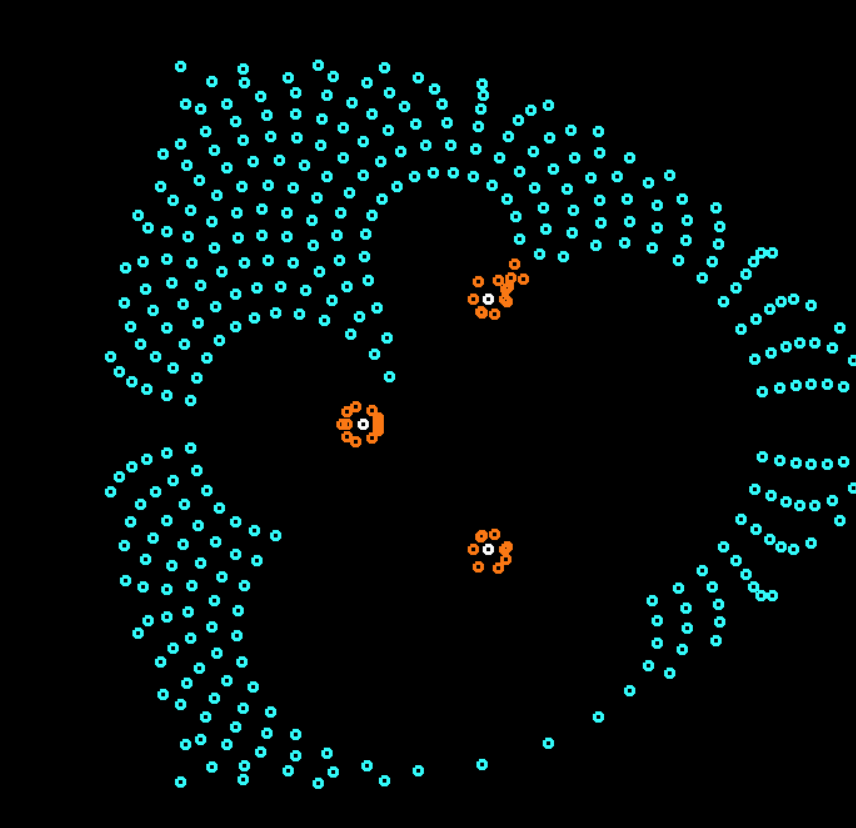
Pozhayluy immediately show a room with a few cars
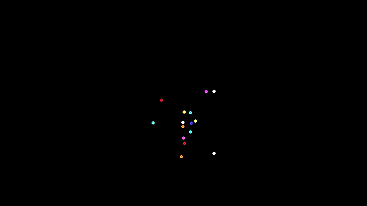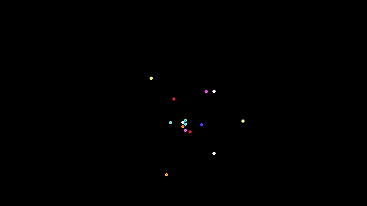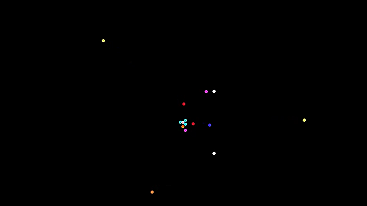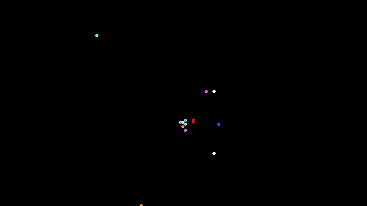
White circles - light bulbs. Colored - automatic machines of different types.
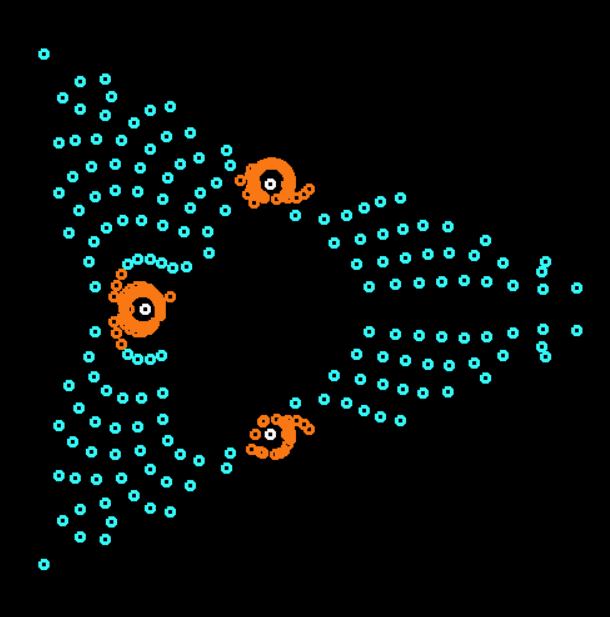
Sometimes a demonstration with the trajectory of each machine gun is more beautiful:
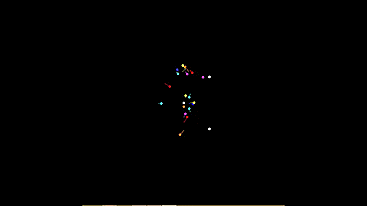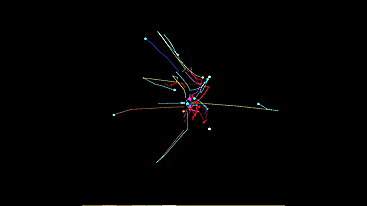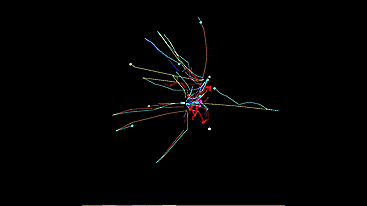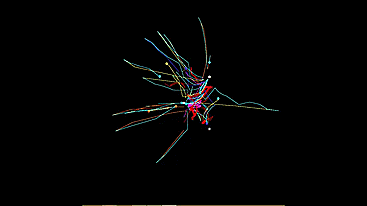
So let's get started . I was the first to implement the light-loving type. There is no need to model the whole system. At first it seemed to me that I could simply divide the power of the light sources by the square of the distance to them, fold the vector and transmit to the machine the resulting vector “direction to the light” as a motion vector. But it turns out quite differently.
Firstly, in the Breitenberg system, the typewriter has two light-sensitive elements. If they are implemented as directional sensors, then they look forward, and if they are undirected, they should not distinguish between forward and backward directions. So I took a plane perpendicular to the motion vector, and reflected “direction to the light” if it pointed back. It turned out such ears, which do not distinguish where the sound came from - in front or behind, but only to the right or left, and what kind of power.
Secondly, the set on wheels cannot move perpendicularly to the side, it has a maximum angle of rotation (per unit of distance traveled), maximum speed and inertia. I added all this by cutting off the angle of the vector of motion relative to the direction vector of the automaton to a certain maximum, cutting it modulo it, and having previously vectorially added them: V_new = Inertia * V_old + (1 - Inertia) * LightDir.
Something like this (C #):
... switch (TypeOfAu) { case 1: calcangle(); // cos sin GetLights(); // ' turn(true); // { lightX = Math.Abs(lightX); // SetMod(); // ( ) if (light > BackToNormalAfterProtectionClarion) Switch("state"); CutMod(); // CutAng(ref lightX, ref lightY); // } turn(false); // break; ... } vx = (1 - inertia) * lightX * Vv + inertia * vx; vy = (1 - inertia) * lightY * Vv + inertia * vy; // Vv - , Result:

As a result, features became noticeable - for example, it can be seen that cars passing exactly in the middle between two light bulbs continue to move. Everything is good, we can create a new type based on this.
Now there will be a fear of the light. To do this, you need to do everything too, but reflect the motion vector relative to the current orientation of the machine (not a reflection relative to its coordinate! Otherwise, you will again get a physically unreal apparatus).
Code Changes
... case 2: ... turn(true); // { ... lightY = -lightY; // } turn(false); break; ... 
The only negative is that such automata escape from the screen and leave behind an empty field. We put them a protective mechanism against runaway - in low light, they will change their behavior to the first model until they return to the light bulbs.
Now let's set up cars with a couple of neurodes. The first will repeat the model of the light-loving machine, but with embedded neurods on the lines. From the sensor, a braking signal will go to the neurode, and from the neurode, the signal will go to the motor. Now the more we light on the sensor, the less signals to the motor - the slower the car goes. Such a system will have the wiring as the first model, but behave more like the second - to run away from the light. But if the speed of the first one decreases with distance from the source, then this will be the opposite: it will accelerate. Correct the code to calculate the motion vector modulus accordingly and voila:

When I made this machine for the first time it seemed to me that it works correctly, but something was wrong ... This is the first version where I mixed up some kind of sign.

It’s more beautiful to watch them in the track recording mode - they draw something like an eye.

Now the next machine. Again we cross wires, but with neurodes on them (in the code - we remove the last reflection of the vector):
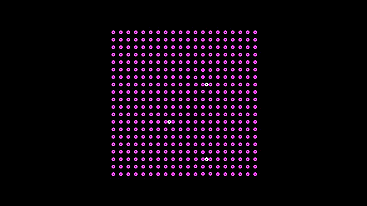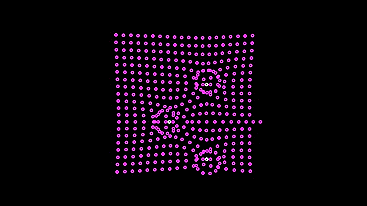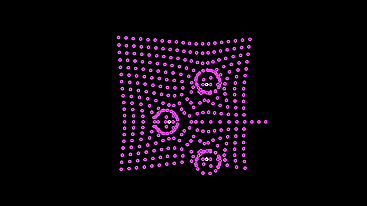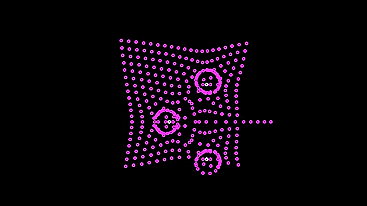
This machine is wiser, it does not break to the light, at the risk of breaking a light bulb (and it would be so in a real model), but stops at a distance when enough light strikes the sensors so that the braking signal completely stops generating signals for the motor.
Number five. Machine with a complex system of neurodes. For a description, you can visit this article , but for now I'll tell you how this is done in simple ways - a barrier in the amount of light is added, and the sign in the reflection operation changes depending on whether the light level is lower than the threshold value, or lower. A real machine should run away like a third when there is little light, and go into the light like a fourth when there is a lot of it. Somewhere there will also be an inner circle, where it will stop altogether - I chose the coefficients for a long time, I often changed them, but I did not achieve a beautiful runaway from the “light edge from the fire”. Anyway, the inner circle of the stop should be wide enough (to occupy more than half of the area) - this is due to the realization of the quadratic light attenuation with increasing distance, so physics is to blame, not me =)

And the last one . This one should change its models according to the opposite principle - to reach for the light when it is not enough, and to run away when there is a lot. Azimov admirers will immediately understand that such a machine will constantly run in a circle on an equipotential line (lines of a constant level of illumination). And if we continue the direct “sensorless” model that I have used so far, the machine will simply reach this line and stop. In the real world, her running in a circle will be due to the fact that one of the eyes is inside the circle, and the other outside, and the internal neurogenic structure will create a new case for the movement algorithm - will make it move perpendicular to the direction of light. In order to simulate this type of automaton, I had to add a real description of two sensors, and in order for one of them to have a value of illumination at some moments below the threshold, when on the other, it was necessary to place them at some distance. The physical distance between sensors is called parallax (for example, between a person’s eyes, or two telescopes in one system). Here is the machine after my dopilov (eyes on gui did not draw).

Code
... case 6: calcangle(); double paralax = 0.01; GetLights((angless) * paralax, (anglecs) * paralax); SetMod(); double tempL = light; // - GetLights((-angless) * paralax, (-anglecs) * paralax); double CicleMaxSpeed = 4; int sw = 0; SetMod(); // - , ... Changing the parallax causes a change in accuracy


For some values, the automaton moves almost in even arcs, while for others, it moves along wavy paths, constantly approaching and then moving away. Similar behavior for robots in a race on the line.
Now let's throw a family of different types of automata on the field.

The first version at the beginning of the article seemed to me somewhat boring, so I first made some light bulbs to go out and light from time to time ... And then I did a mixing algorithm , which once in a while changed the type of machine to some other one, so so that it goes through "all incarnations":

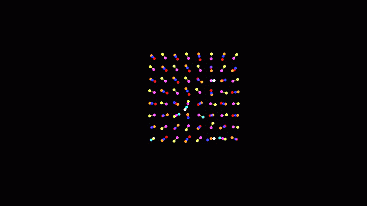
Without all this, you can look at the grid of all types in one field.


After that, I thought about the machines having a physical size (so that they would not pass through each other), but calculating collisions is a difficult task for a computer, especially with such a large number of participants, so I just took a couple of shots and turned off the mode


In principle, it was all the same, only the machines pushed around their asymptotic trajectories, and were not exactly on them, that's all. Let's return to the world without collisions)
Consider now the system on a long exposure - what does it want?
The switching mode of the light bulbs does not allow the system to remain a static picture, but the light fans have tried very hard - they are hooked to their lamps and do not have time to run away from them during the period when they are turned off.

Their wiser version is in time, and as a result there is a flock that moves along a cyclic path between the three lamps.


Photoplastic work differently. Since the protection system returns them at the same speed as their removal rate - at each level, they form an even noise, about half of the machines are slowly removed, the other half returns in protection mode.

With their version pumped by neurodes, the situation is different - they quickly fly away, but slowly gather back. I expected that they will eventually form an even narrowing circle, but no. They retain asymmetrical shape, and sometimes give beautiful pictures

Sometimes they look like the same chaos:

The changing machine most often behaves the same way. But in the end, they stumble into very small groups that travel quite a lot from the light bulb and to the light bulb along such rails.

In addition to several machines that caught "their own wave" and spinning on the right side of the room. I waited for them to join one of the three clans, but after 2 hours of simulation this did not happen, it seems that this is the case of strange dynamically stable trajectories, like that asteroid that flies around the gravitational well of the earth, then to the right or to the left.
Cyclic automatons showed a telephone receiver (or a smiling face?), Lumped together, and began to turn and unfold the tentacles in turns to the lamps currently in operation.
Rozhitsa

Stable mode

In the meantime, while the long-running simulations were going, I thought about other options and added three more non-standard types . They are guided not by light, but by other automata.
The first of them is waiting for automata to appear in the neighborhood, and is trying to follow the nearest one. The rest of the time it is worth and sad.

You can call them dogs, because they need owners. I put them on the field with the 5th type, otherwise they would all just stand.
Another type - averages the coordinates of many automata and runs into the crowd - "extrovert."

His antipode is an introvert who tries to keep his distance.

At the beginning, the grid has a translational symmetry and the central automata have no place to go - in any direction they would approach the neighbors, so they wait for the extreme ones to scatter. It looks interesting in the track mode - a shaggy IC is obtained.

Now put all 9 types (including new ones) and look at the grid. (type mixing included)
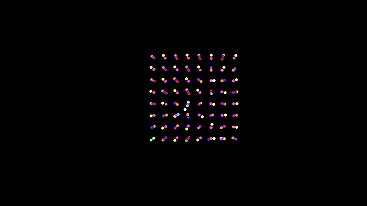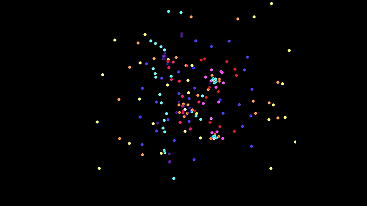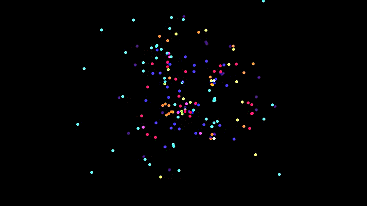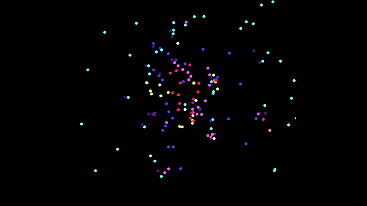
And in the track mode, they draw a dandelion


In the center I placed a light source with a negative power value. I don’t know what I expected, but the anti-light though lures the usually fleeing automata, but their behavior does not become similar to the “crossed” analogues of light lovers, but it turns out something third, more complex.
More dandelions that turned out.




So, too, it turns dandelion. I became interested when I saw the drawing of the “cobweb” in the corner of one of the simulations - the fugitives fled into the distance with rays, and the dogs did not have time for them, and moved from one to the other with half-arches. I thought that if you do it so massively, you get a cobweb, as it is always painted. Therefore, I threw into the room only these two types of machine guns - but something went wrong. In any configuration, the system is unstable and the dogs collapse in some direction, as a result, just another dandelion comes out - and no cobwebs.

Added another lamp.


But ... Um ... Porcupine?

In general, the behavior, as for my taste, is really quite complicated. But let's move on. Let's try to show nonlinearity . A runaway version works well for this. The divergence from the sphere (which is an equipotential in illumination surface around the bulb) almost guarantees the appearance of deterministic chaos.
Let's run the same grid, but very small in size - so that the initial conditions for the machines differ only slightly (automata leave almost from one point), and see how the system develops and what it will show us.


Now let's run the same small grid, but with different types of machines and enabled type mixing.

Such interesting pictures are obtained ... For a change, you can change the visualization model , say, connect all the cars with lines (as if they would pull one long string). So it is more convenient to observe exactly how the algorithm crumples the initially flat grid of machines, and where it sends its different parts - how they migrate around their world.

Get stuck like the one in the media player.
Sometimes interesting shapes appear.




In general , such a simulator. Feel free to offer your ideas and suggestions in the comments, what else can you add, or what experiment to put. Personally, I think the resulting piece is a convenient demonstration for the theory of nonlinear systems - in it you can look for assymptotics, divergences, curious patterns, showing the complexity of simple systems ... People can use the concept both in automation and beginners in building BEAM robots - to understand the essence, and in general - see color pictures.
All good, robotopsihologi. It's all.



Source: https://habr.com/ru/post/342154/
All Articles