Integrating the equations of motion

A physics simulation makes small predictions based on the laws of physics. These predictions are actually quite simple, something like “if an object is right here and it moves with such speed in this direction, then in a short period of time it will be right here.” We create such predictions using a mathematical technique called integration.

The topic of this article will be the implementation of such integration.
')

Integrating the equations of motion

You may remember from a high school or university course that force is equal to the product of mass and acceleration.

$$

$$F = ma$$

Let us transform this equation and see that the acceleration is equal to the force divided by the mass. This is in line with our intuitive expectations, because heavy objects are harder to throw.

$$

$$a = f / ma = f / m$$

Acceleration is the rate of change of speed over time:

$$

$$dv / dt = a = F / m$$

Similarly, speed is the rate of change of position over time:

$$

$$dx / dt = v$$

This means that if we know the current position and speed of the object, as well as the forces applied to it, we can integrate to find its position and speed at a certain point in time.

Numerical integration

If you have not studied the differential equations at the university, then you can breathe easy - you are almost in the same situation as those who studied them, because we will not solve differential equations analytically. Instead, we will seek a solution by numerical integration .

Here's how numerical integration works: first, let's start from the starting position and speed, then take a small step forward to find the speed and position in the future. Then we repeat this, moving forward in small steps, using the result of previous calculations as the starting point of the following.

But how do we find the change in speed and position at each step?

The answer lies in the equations of motion .

Let's call our current time t , and the time step dt or "delta time".

Now we can present the equations of motion in a form that everyone understands:

  acceleration = force / mass
     position change = speed * dt
     speed change = acceleration * dt 

Intuitively, this is understandable: if you are in a car moving at a speed of 60 km / h, then in one hour you will drive 60 km. Similarly, a car accelerating at 10 km / h per second, after 10 seconds, will move 100 km / h faster.

Of course, this logic is preserved only when the acceleration and speed are constant. But even if they change, then this is a good approximation to begin with.

Let's present it in the code. We start with a stationary object weighing one kilogram and apply a constant force of 10 kN (kilonewtons) to it and take a step forward, assuming that one time step is equal to one second:

double t = 0.0; float dt = 1.0f; float velocity = 0.0f; float position = 0.0f; float force = 10.0f; float mass = 1.0f; while ( t <= 10.0 ) { position = position + velocity * dt; velocity = velocity + ( force / mass ) * dt; t += dt; } 

Here is the result:

  t=0: position = 0 velocity = 0 t=1: position = 0 velocity = 10 t=2: position = 10 velocity = 20 t=3: position = 30 velocity = 30 t=4: position = 60 velocity = 40 t=5: position = 100 velocity = 50 t=6: position = 150 velocity = 60 t=7: position = 210 velocity = 70 t=8: position = 280 velocity = 80 t=9: position = 360 velocity = 90 t=10: position = 450 velocity = 100 

As you can see, at every step we know both the position and the speed of the object. This is numerical integration.

Explicit Euler Method

The kind of integration that we just used is called the explicit Euler method .

It is named after the Swiss mathematician Leonard Euler , who first discovered this technique.

Euler integration is the simplest numerical integration technique. It is 100% accurate only when the rate of change during the time step is constant.

Since in the example above the acceleration is constant, the integration of speed is performed without errors. However, we also integrate the speed to obtain the position, and the speed increases due to acceleration. This means that an error occurs in the integrated position.

But how big is this mistake? Let's find out!

There is an analytical solution to the movement of an object with constant acceleration. We can use it to compare a numerically integrated position with the exact result:

  s = ut + 0.5at ^ 2
     s = 0.0 * t + 0.5at ^ 2
     s = 0.5 (10) (10 ^ 2)
     s = 0.5 (10) (100)
     s = 500 meters 

After 10 seconds, the object should have moved 500 meters, but the apparent Euler method gives us a result of 450. That is, an error of as much as 50 meters in just 10 seconds!

It seems that this is incredibly bad, but in games, usually for a physics step, not such a large time interval is taken. In fact, physics is usually calculated with a frequency approximately equal to the frame rate of the display.

If you set the step dt = ¹ ⁄ ₁₀₀ , then we get a much better result:

  t=9.90: position = 489.552155 velocity = 98.999062 t=9.91: position = 490.542145 velocity = 99.099060 t=9.92: position = 491.533142 velocity = 99.199059 t=9.93: position = 492.525146 velocity = 99.299057 t=9.94: position = 493.518127 velocity = 99.399055 t=9.95: position = 494.512115 velocity = 99.499054 t=9.96: position = 495.507111 velocity = 99.599052 t=9.97: position = 496.503113 velocity = 99.699051 t=9.98: position = 497.500092 velocity = 99.799049 t=9.99: position = 498.498077 velocity = 99.899048 t=10.00: position = 499.497070 velocity = 99.999046 

As you can see, this is a fairly good result, definitely enough to play.

Why Euler's explicit method is not (always) good

With a sufficiently small time step, the explicit Euler method with constant acceleration gives quite decent results, but what happens if the acceleration is not constant?

A good example of variable acceleration is the spring shock absorber system .

In this system, the mass is attached to the spring, and its movement is extinguished by something like friction. There is a force proportional to the distance to the object, which attracts it to the starting point, and a force proportional to the speed of the object, but directed in the opposite direction, which slows it down.

Here, the acceleration during a time step changes absolutely exactly, but this ever-changing function is a combination of position and speed, which themselves constantly change in a time step.

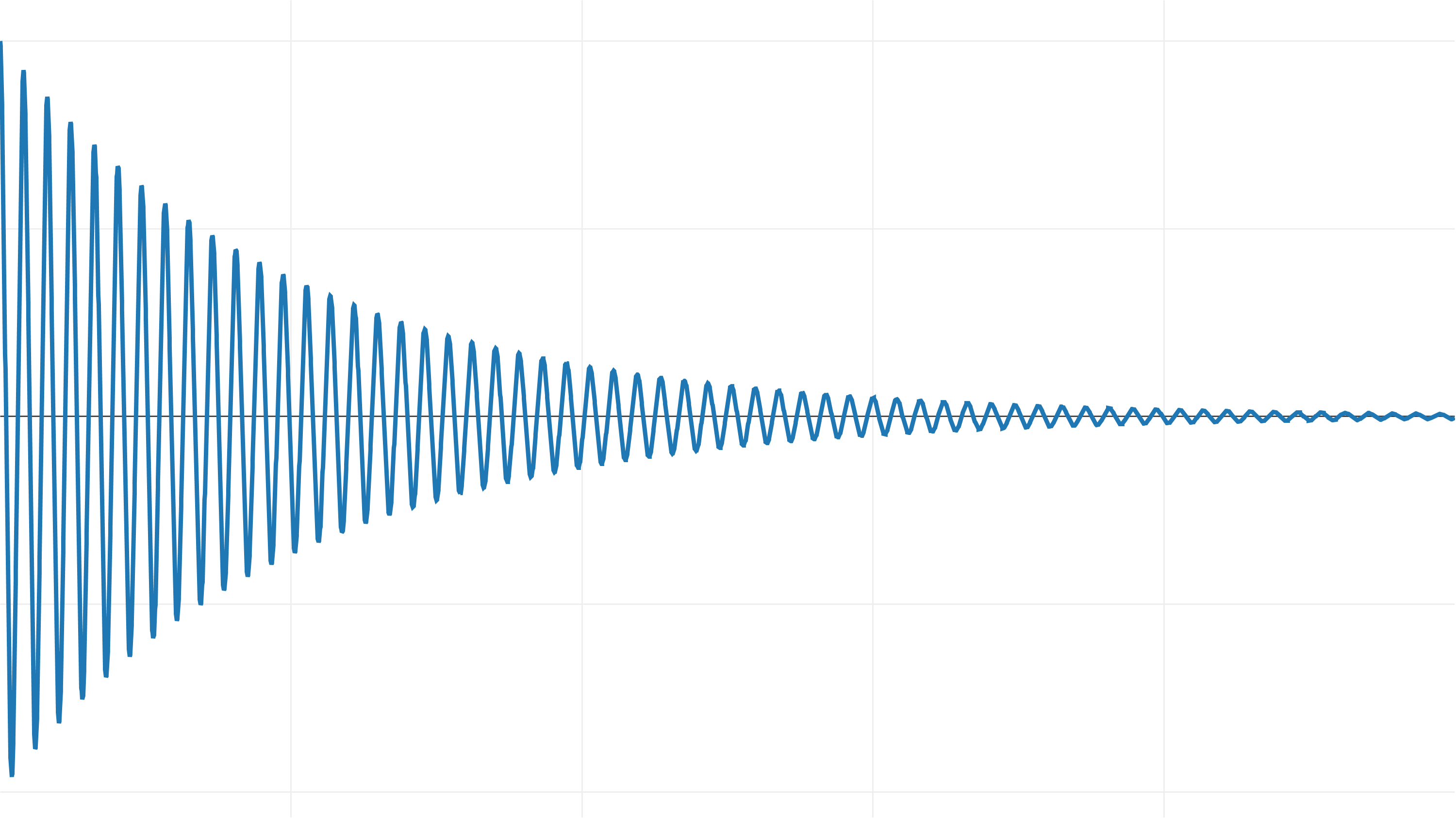
Here is an example of a harmonic oscillator with attenuation . This is a well-studied problem, and for it there is an analytical solution that can be used to verify the result of numerical integration.

Let's start with a weakly damped system, in which the mass oscillates near the starting point, gradually slowing down.

Here are the input parameters of the mass-spring system:

• Weight: 1 kilogram
• Starting position: 1000 meters from the starting point
• Coefficient of elasticity according to Hooke's law: k = 15
• Hooke's damping coefficient: b = 0.1

And here is the exact solution graph:



If for the integration of this system we apply the explicit Euler method, then we obtain the following result, which I scaled vertically:



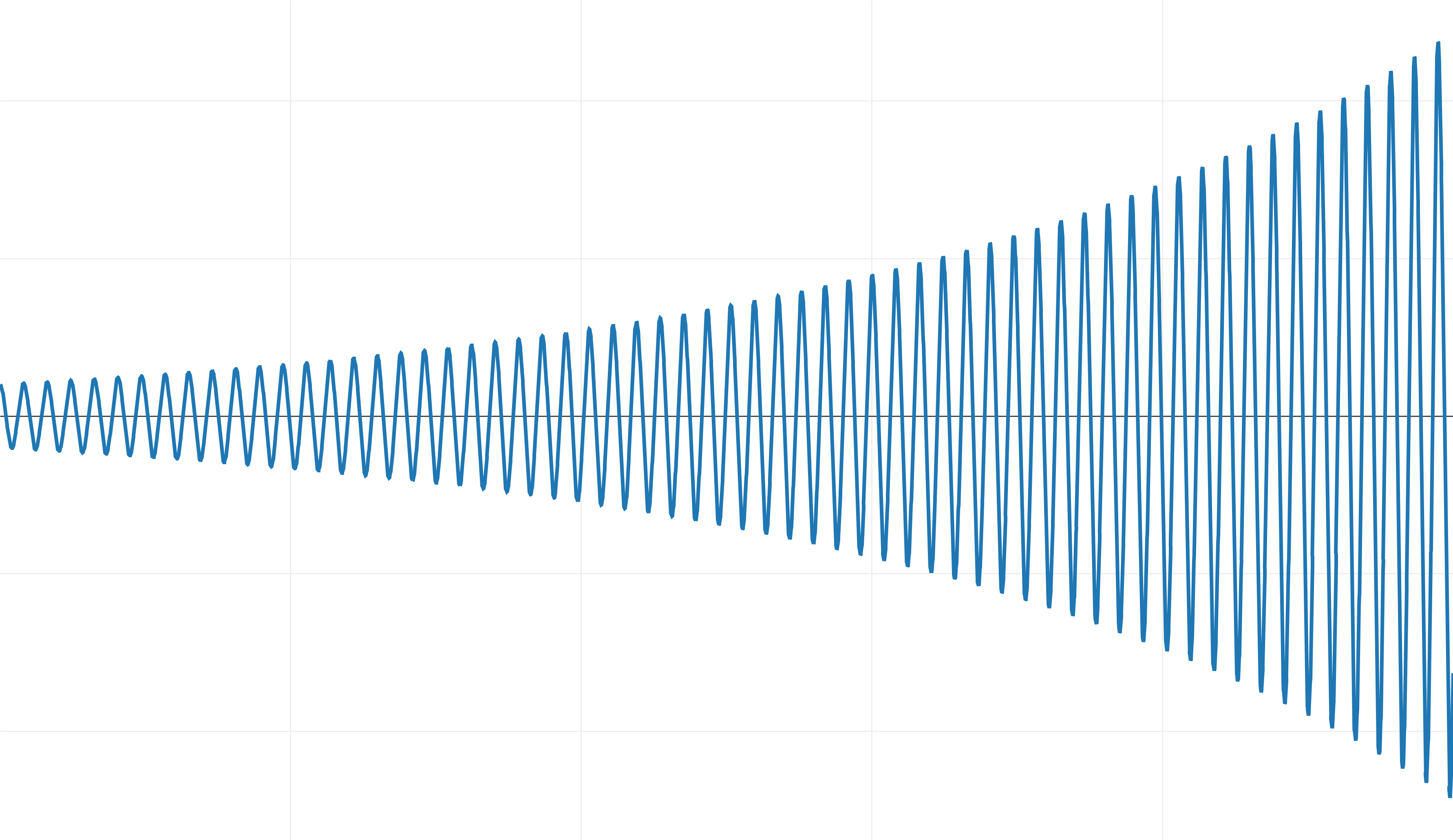
Instead of attenuation and convergence with the starting point, the system gains energy over time!

When integrating by the explicit Euler method and with dt = ¹ ⁄ _100, this system is unstable.

Unfortunately, since we are already integrating with a small time step, we do not have practical ways to increase accuracy. Even if we reduce the time step, there will always be a coefficient of elasticity k, at which we get this behavior.

Euler's Symplectic Method

We can consider another integrator, the Euler symplectic method .

Most commercial gaming physics engines use this integrator.

The transition from the explicit to the symplectic method of Euler consists only in the replacement of:

  position += velocity * dt; velocity += acceleration * dt; 

on:

  velocity += acceleration * dt; position += velocity * dt; 

Using the Euler symplectic integrator with dt = ¹ ⁄ ₁₀₀ for the spring shock absorber system gives a stable result, very close to the exact solution:



Even though the Euler symplectic method has the same degree of accuracy as the explicit method (degree 1), we get a much better result when integrating the equations of motion, because it is symplectic .

There are many other integration methods.

And now for something completely different.

The implicit Euler method is an integration method that is well suited for integrating rigid equations that become unstable with other methods. Its disadvantage is that it requires solving a system of equations at each time step.

Integration Verlet provides greater accuracy than the implicit Euler method, and requires less memory when simulating a large number of particles. This is a second degree integrator, which is also symplectic.

There is a whole family of integrators, called Runge-Kutta methods . In fact, the explicit Euler method is considered part of this family, but it includes integrators of higher order, the most classic of which is the Runge-Kutta method of order 4 (Runge Kutta order 4) or simply RK4 .

This family of integrators is named after the German physicists who discovered them: Karl Runge and Martin Kutta .

RK4 is a fourth-order integrator, that is, the accumulated error is of the order of the fourth derivative. This makes the method very accurate, much more accurate than the explicit and implicit Euler methods that have only the first order.

But although it is more accurate, one cannot say that RK4 automatically becomes the “best” integrator, or even that it is better than Euler’s symplectic method. Everything is much more complicated. However, this is a rather interesting integrator and is worth exploring.

RK4 implementation

There are already many explanations for the mathematics used in RK4. For example: here , here and here . I strongly recommend studying its derivation and understand how and why it works at the mathematical level. But I understand that the target audience of this article is programmers, not mathematicians, therefore we will consider only implementation here. So let's get started.

Before we begin, let's set the state of an object as a struct in C ++ so that it is convenient to store the position and speed in one place:

  struct State { float x; //  float v; //  }; 

We also need a structure to store the derived state values:

  struct Derivative { float dx; // dx/dt =  float dv; // dv/dt =  }; 

Now we need a function to calculate the state of physics from t to t + dt using one set of derivatives, and then to calculate the derivatives in the new state:

  Derivative evaluate( const State & initial, double t, float dt, const Derivative & d ) { State state; state.x = initial.x + d.dx*dt; state.v = initial.v + d.dv*dt; Derivative output; output.dx = state.v; output.dv = acceleration( state, t+dt ); return output; } 

The acceleration function controls the entire simulation. Let's use it in the spring shock absorber system and return the acceleration for a unit mass:

  float acceleration( const State & state, double t ) { const float k = 15.0f; const float b = 0.1f; return -k * state.x - b * state.v; } 

What needs to be written here, of course, depends on the simulation, but it is necessary to structure the simulation so that it is possible to calculate the acceleration inside this method for a given state and time, otherwise it will not work for the integrator RK4.

Finally, we get the integration procedure itself:

  void integrate( State & state, double t, float dt ) { Derivative a,b,c,d; a = evaluate( state, t, 0.0f, Derivative() ); b = evaluate( state, t, dt*0.5f, a ); c = evaluate( state, t, dt*0.5f, b ); d = evaluate( state, t, dt, c ); float dxdt = 1.0f / 6.0f * ( a.dx + 2.0f * ( b.dx + c.dx ) + d.dx ); float dvdt = 1.0f / 6.0f * ( a.dv + 2.0f * ( b.dv + c.dv ) + d.dv ); state.x = state.x + dxdt * dt; state.v = state.v + dvdt * dt; } 

The RK4 integrator samples the derivative at four points to determine the curvature. Notice how the derivative a is used in calculating b, b is used in calculating c, and c for d. This transfer of the current derivative to the next calculation gives the integrator RK4 its accuracy.

It is important that each of these derivatives a, b, c and d will be different when the rate of change in these quantities is a function of time or a function of the state itself. For example, in our spring damper system, acceleration is a function of the current position and speed, which vary in time steps.

After calculating the four derivatives, the best total derivative is calculated as a weighted sum obtained from the expansion in a Taylor series . This combined derivative is used to move the position and speed forward in time, just as we did in the explicit Euler integrator.

Comparison of the symplectic method of Euler and RK4

Let's test the integrator RK4.

Obviously, since he is a higher-order integrator (fourth versus the first), he will be visually more accurate than Euler’s symplectic method, right?



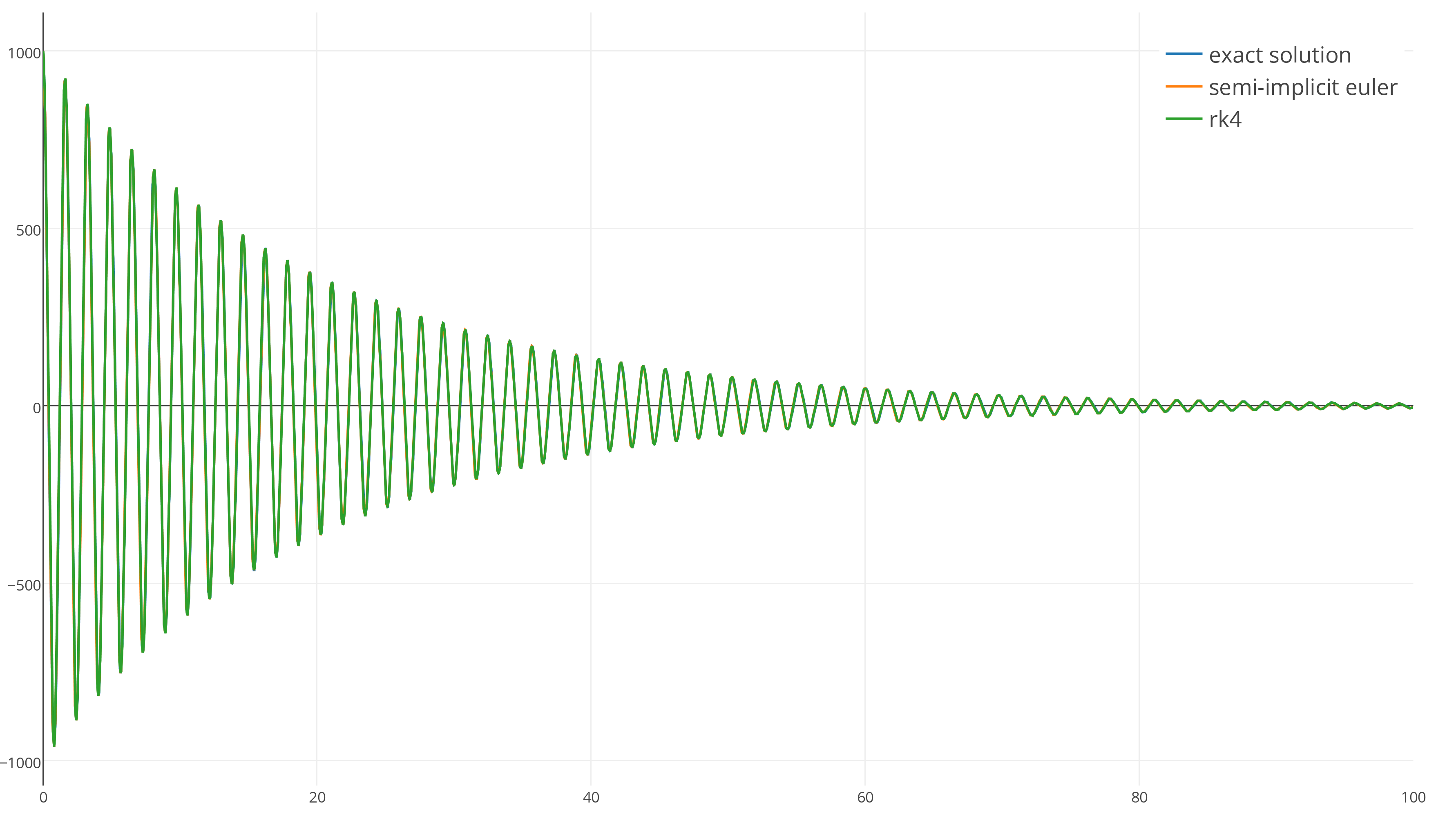
It is not true . Both integrators are so close to the exact result that with such a scale it is almost impossible to find a difference between them. Both integrators are stable and repeat the exact solution very well with dt = ¹ ₁₀₀ .


With the increase it can be seen that RK4 is indeed more accurate than the symplectic method of Euler, but is this precision worth the complexity and extra runtime of RK4? It's hard to judge.

Let's try and see if we can find a significant difference between the two integrators. Unfortunately, we will not be able to observe this system for a long time, because it quickly decays to zero, so let's move on to a simple harmonic oscillator that oscillates infinitely and without attenuation.

Here is the exact result to which we will strive:



To complicate the task of integrators, let's increase the time step to 0.1 seconds.

Now let's launch integrators for 90 seconds and zoom in:



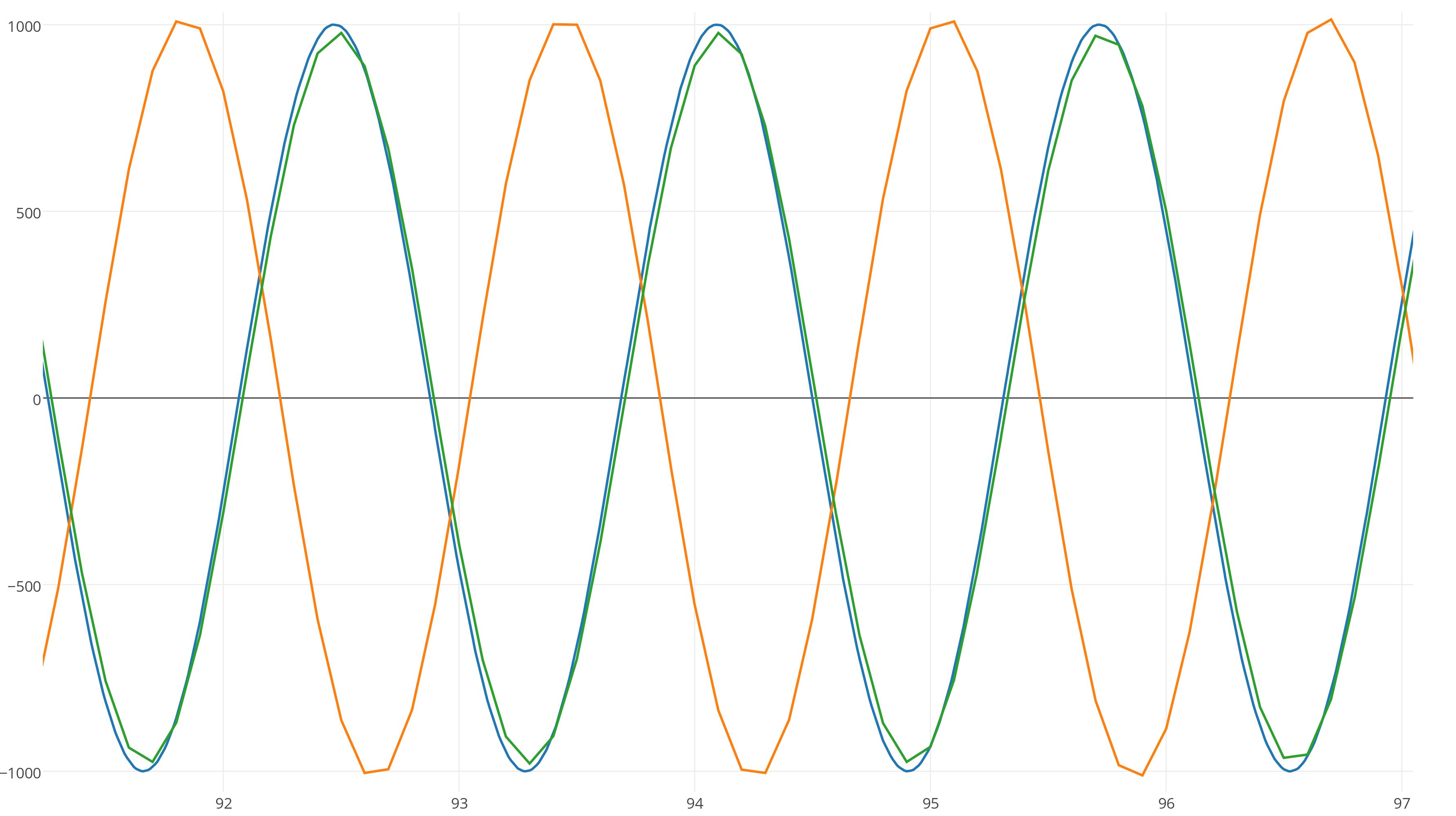
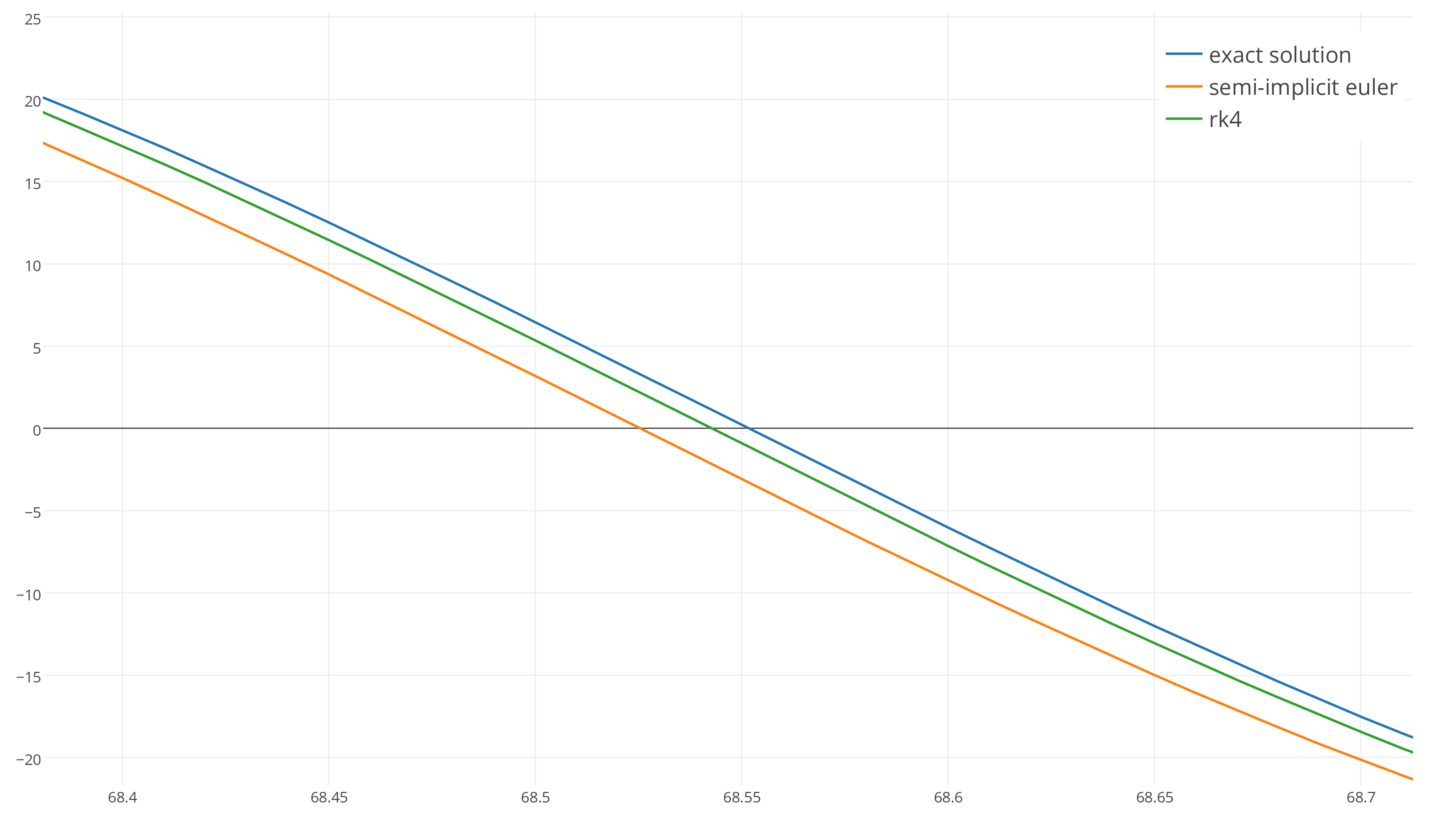
After 90 seconds, Euler's symplectic method (the orange curve) shifted in phase with respect to the exact solution, because its frequency was slightly different, while the green RK4 curve corresponds to the frequency, but it loses energy!

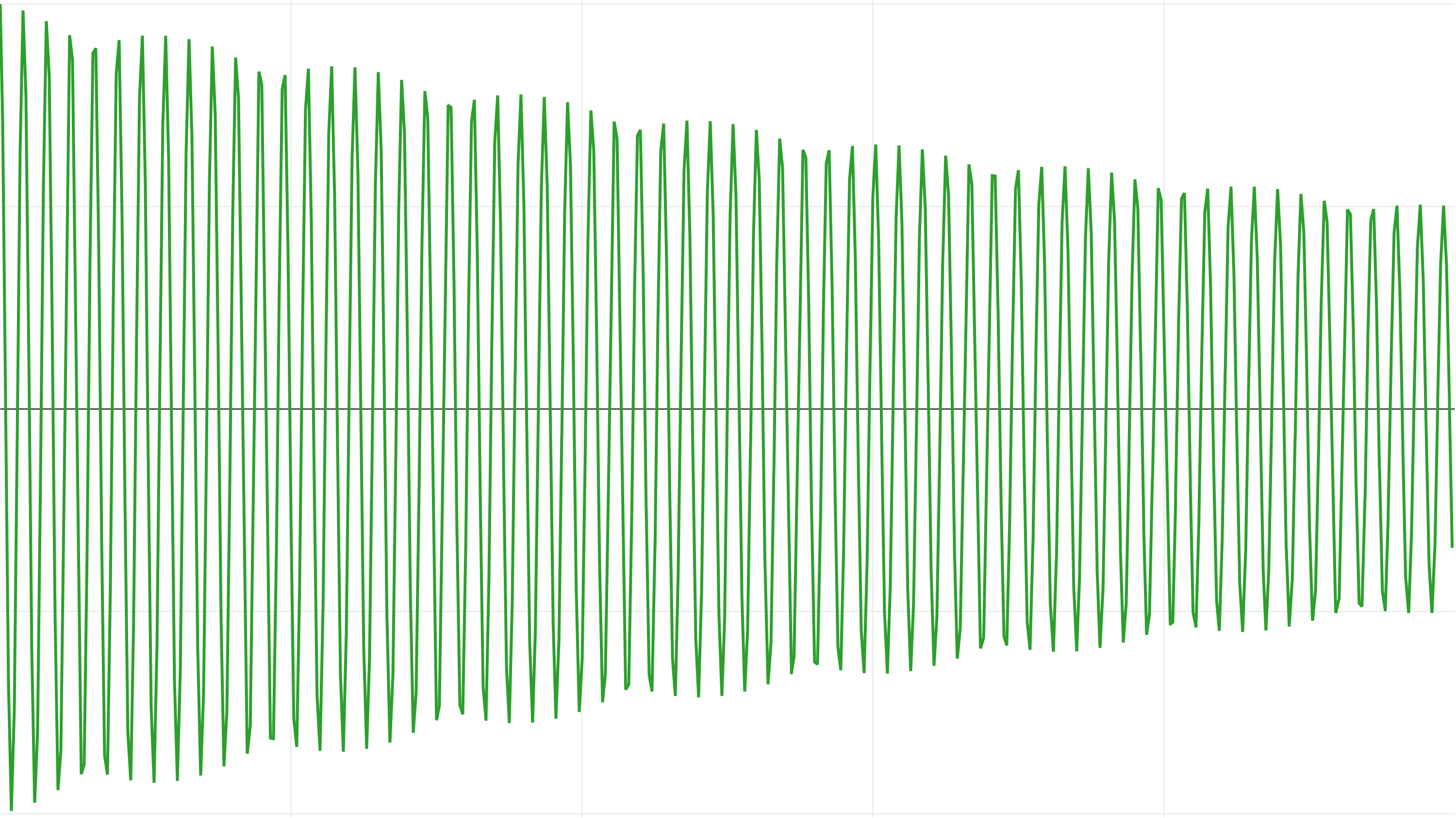
We can clearly notice this by increasing the time step to 0.25 seconds.

RK4 retains the correct frequency, but loses energy:



And the Euler symplectic method on average saves energy much better:



But from shifts from phase. What an interesting result! As you can see, if the RK4 has a higher order of accuracy, then it is not necessarily "better." There are many nuances in this matter.

Conclusion

We implemented three different integrators and compared the results.

1. Explicit Euler Method
2. Euler's Symplectic Method
3. Runge-Kutta method of order 4 (RK4)

So which integrator should be used in the game?

I recommend the Euler symplectic method . It is “cheap” and simple to implement, much more stable than the explicit Euler method and, on average, tends to conserve energy even under close to extreme conditions.

If you really need greater accuracy than the Euler symplectic method, I recommend looking at higher order symplectic integrators designed for Hamiltonian systems . In this way, you will learn more advanced high order integration techniques that are better suited for simulations than RK4.

Finally, if you still write this in the game:

  position + = velocity * dt;
     velocity + = acceleration * dt; 

Then take a second and replace these lines with:

  velocity + = acceleration * dt;
     position + = velocity * dt; 

Believe me, you'll be glad of it.