Chronology of CO level in the atmosphere of the USA (solution of the Kaggle problem using Python + Feature Engineering)
I want to share the experience of solving the problem of machine learning and data analysis from Kaggle. This article is positioned as a guide for beginners on the example of not quite a simple task.
Data retrieval
The data sample contains about 8.5 million rows and 29 columns. Here are some of the parameters:
')

Task
Import Libraries
Next, you need to check the source data for the presence of gaps
We derive the percentage ratio of the number of gaps in each of the parameters. Based on the results below, the presence of gaps in the parameters ['aqi', 'local_site_name', 'cbsa_name'] can be seen.
From the description of the attached data set, I concluded that we can ignore these parameters. Therefore, it is necessary to “cross out” these parameters from the data set.
Identify dependencies on the source dataset
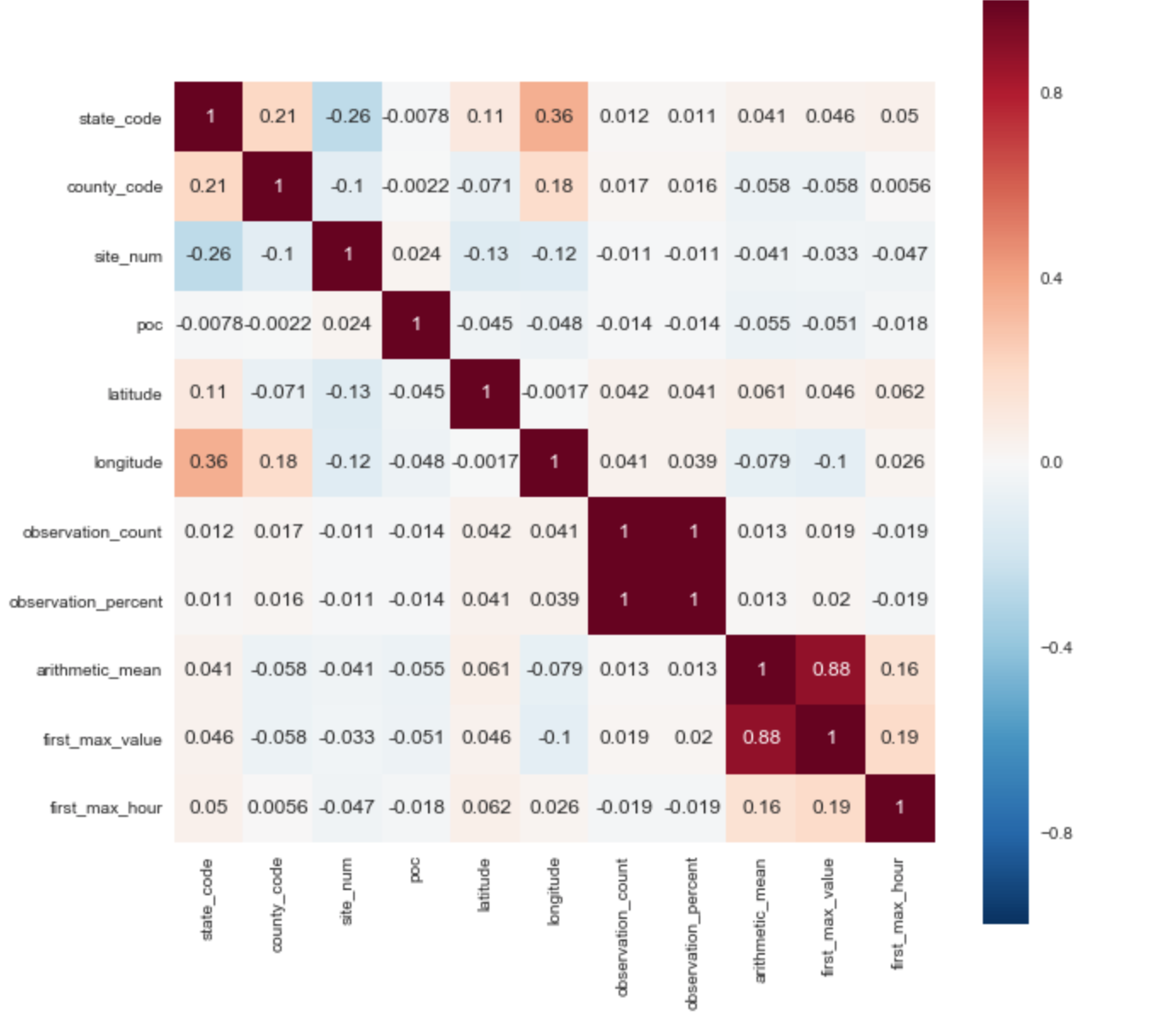
For the target variable, I selected the ['arithmetic_mean'] parameter. Based on the correlation matrix, you can immediately identify 2 positive correlations with the target parameter: ['arithmetic_mean'] and ['first_max_hour'], ['first_max_hour'].
From the description of the data set, it follows that “first_max_value” is the highest figure of the day, and “first_max_hour” is the hour when the highest indicator was recorded.
Conversion of source parameters:
For the correct operation of the algorithm, it is necessary to convert the categorical attribute into a numerical one. Several parameters are immediately apparent to the data presented above:
"Pollutant_standard", "event_type", "address".
Feature Engineering
In the data set we have the date and time. To identify new dependencies and
increase the prediction accuracy, you must enter the seasonality parameter of the seasons.
Also denote each year in the chronological chain as a separate parameter.
After transformations, the dimension of the data set was significantly increased, as the number of parameters increased from 22 to 114.
Below is the fragment (1/4 part of the correlation matrix of the final data set):

Prediction model:
As a tool for constructing a prediction hypothesis, I opted for linear regression. The prediction accuracy on the initial data set ranged from 17% to 22%. The accuracy of the prediction after the introduction of new variables and the transformation of the data set was:

Data Visualization:
USA map with points where measurements were taken:

The states with the highest average amount of CO emissions for all time (the red line indicates the maximum acceptable level for living):
Chronology of the development of the level of emissions:

Data retrieval
The data sample contains about 8.5 million rows and 29 columns. Here are some of the parameters:
')
- Latitude Latitude
- Longitude-longitude
- Sampling method-method_name
- Date and time of sampling-date_local

Task
- Find the parameters that most affect the level of CO in the atmosphere.
- Creating a hypothesis predicting the level of CO in the atmosphere.
- Create a few simple visualizations.
Import Libraries
import pandas as pd import matplotlib.pyplot as plt from sklearn import preprocessing from mpl_toolkits.basemap import Basemap import matplotlib.pyplot as plt import seaborn as sns import numpy as np from sklearn import preprocessing import warnings warnings.filterwarnings('ignore') import random as rn from sklearn.cross_validation import train_test_split from sklearn.naive_bayes import GaussianNB from sklearn.ensemble import RandomForestRegressor from sklearn.neighbors import KNeighborsClassifier from sklearn.linear_model import LogisticRegression from sklearn import svm Next, you need to check the source data for the presence of gaps
We derive the percentage ratio of the number of gaps in each of the parameters. Based on the results below, the presence of gaps in the parameters ['aqi', 'local_site_name', 'cbsa_name'] can be seen.
(data.isnull().sum()/len(data)*100).sort_values(ascending=False) method_code 50.011581 aqi 49.988419 local_site_name 27.232437 cbsa_name 2.442745 date_of_last_change 0.000000 date_local 0.000000 county_code 0.000000 site_num 0.000000 parameter_code 0.000000 poc 0.000000 latitude 0.000000 longitude 0.000000 ... From the description of the attached data set, I concluded that we can ignore these parameters. Therefore, it is necessary to “cross out” these parameters from the data set.
def del_data_func(data,columns): for column_name in columns: del data[column_name] del_list = data[['method_code','aqi','local_site_name','cbsa_name','parameter_code', 'units_of_measure','parameter_name']] del_data_func (data, del_list) Identify dependencies on the source dataset

For the target variable, I selected the ['arithmetic_mean'] parameter. Based on the correlation matrix, you can immediately identify 2 positive correlations with the target parameter: ['arithmetic_mean'] and ['first_max_hour'], ['first_max_hour'].
From the description of the data set, it follows that “first_max_value” is the highest figure of the day, and “first_max_hour” is the hour when the highest indicator was recorded.
Conversion of source parameters:
For the correct operation of the algorithm, it is necessary to convert the categorical attribute into a numerical one. Several parameters are immediately apparent to the data presented above:
"Pollutant_standard", "event_type", "address".
data['county_name'] = data['county_name'].factorize()[0] data['pollutant_standard'] = data['pollutant_standard'].factorize()[0] data['event_type'] = data['event_type'].factorize()[0] data['method_name'] = data['method_name'].factorize()[0] data['address'] = data['address'].factorize()[0] data['state_name'] = data['state_name'].factorize()[0] data['county_name'] = data['county_name'].factorize()[0] data['city_name'] = data['city_name'].factorize()[0] Feature Engineering
In the data set we have the date and time. To identify new dependencies and
increase the prediction accuracy, you must enter the seasonality parameter of the seasons.
data['season'] = data['date_local'].apply(lambda x: 'winter' if (x[5:7] =='01' or x[5:7] =='02' or x[5:7] =='12') else x) data['season'] = data['season'].apply(lambda x: 'autumn' if (x[5:7] =='09' or x[5:7] =='10' or x[5:7] =='11') else x) data['season'] = data['season'].apply(lambda x: 'summer' if (x[5:7] =='06' or x[5:7] =='07' or x[5:7] =='08') else x) data['season'] = data['season'].apply(lambda x: 'spring' if (x[5:7] =='03' or x[5:7] =='04' or x[5:7] =='05') else x) data['season'].replace("winter",1,inplace= True) data['season'].replace("spring",2,inplace = True) data['season'].replace("summer",3,inplace=True) data['season'].replace("autumn",4,inplace=True) data["winter"] = data["season"].apply(lambda x: 1 if x==1 else 0) data["spring"] = data["season"].apply(lambda x: 1 if x==2 else 0) data["summer"] = data["season"].apply(lambda x: 1 if x==3 else 0) data["autumn"] = data["season"].apply(lambda x: 1 if x==4 else 0) Also denote each year in the chronological chain as a separate parameter.
data['date_local'] = data['date_local'].map(lambda x: str(x)[:4]) data["1990"] = data["date_local"].apply(lambda x: 1 if x=="1990" else 0) data["1991"] = data["date_local"].apply(lambda x: 1 if x=="1991" else 0) data["1992"] = data["date_local"].apply(lambda x: 1 if x=="1992" else 0) data["1993"] = data["date_local"].apply(lambda x: 1 if x=="1993" else 0) data["1994"] = data["date_local"].apply(lambda x: 1 if x=="1994" else 0) data["1995"] = data["date_local"].apply(lambda x: 1 if x=="1995" else 0) data["1996"] = data["date_local"].apply(lambda x: 1 if x=="1996" else 0) data["1997"] = data["date_local"].apply(lambda x: 1 if x=="1997" else 0) data["1998"] = data["date_local"].apply(lambda x: 1 if x=="1998" else 0) data["1999"] = data["date_local"].apply(lambda x: 1 if x=="1999" else 0) data["2000"] = data["date_local"].apply(lambda x: 1 if x=="2000" else 0) data["2001"] = data["date_local"].apply(lambda x: 1 if x=="2001" else 0) data["2002"] = data["date_local"].apply(lambda x: 1 if x=="2002" else 0) data["2003"] = data["date_local"].apply(lambda x: 1 if x=="2003" else 0) data["2004"] = data["date_local"].apply(lambda x: 1 if x=="2004" else 0) data["2005"] = data["date_local"].apply(lambda x: 1 if x=="2005" else 0) data["2006"] = data["date_local"].apply(lambda x: 1 if x=="2006" else 0) data["2007"] = data["date_local"].apply(lambda x: 1 if x=="2007" else 0) data["2008"] = data["date_local"].apply(lambda x: 1 if x=="2008" else 0) data["2009"] = data["date_local"].apply(lambda x: 1 if x=="2009" else 0) data["2010"] = data["date_local"].apply(lambda x: 1 if x=="2010" else 0) data["2011"] = data["date_local"].apply(lambda x: 1 if x=="2011" else 0) data["2012"] = data["date_local"].apply(lambda x: 1 if x=="2012" else 0) data["2013"] = data["date_local"].apply(lambda x: 1 if x=="2013" else 0) data["2014"] = data["date_local"].apply(lambda x: 1 if x=="2014" else 0) data["2015"] = data["date_local"].apply(lambda x: 1 if x=="2015" else 0) data["2016"] = data["date_local"].apply(lambda x: 1 if x=="2016" else 0) data["2017"] = data["date_local"].apply(lambda x: 1 if x=="2017" else 0) After transformations, the dimension of the data set was significantly increased, as the number of parameters increased from 22 to 114.
Below is the fragment (1/4 part of the correlation matrix of the final data set):

Prediction model:
As a tool for constructing a prediction hypothesis, I opted for linear regression. The prediction accuracy on the initial data set ranged from 17% to 22%. The accuracy of the prediction after the introduction of new variables and the transformation of the data set was:

Data Visualization:
USA map with points where measurements were taken:
m = Basemap(llcrnrlon=-119,llcrnrlat=22,urcrnrlon=-64,urcrnrlat=49, projection='lcc',lat_1=33,lat_2=45,lon_0=-95) longitudes = data["longitude"].tolist() latitudes = data["latitude"].tolist() x,y = m(longitudes,latitudes) fig = plt.figure(figsize=(12,10)) plt.title("Polution areas") m.plot(x, y, "o", markersize = 3, color = 'red') m.drawcoastlines() m.fillcontinents(color='white',lake_color='aqua') m.drawmapboundary() m.drawstates() m.drawcountries() plt.show() 
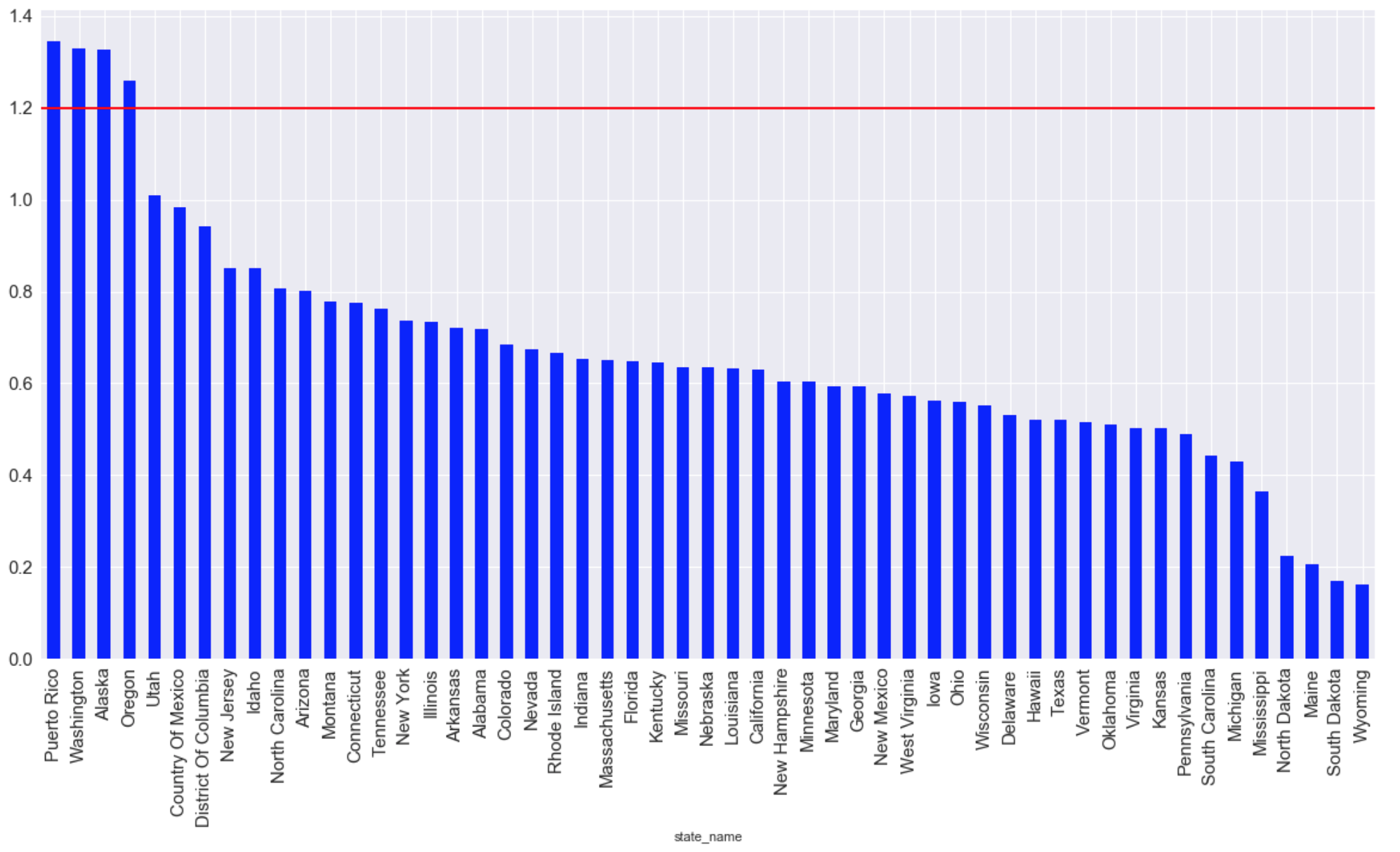
The states with the highest average amount of CO emissions for all time (the red line indicates the maximum acceptable level for living):
graph = plt.figure(figsize=(20, 10)) graph = data.groupby(['state_name'])['arithmetic_mean'].mean() graph = graph.sort_values(ascending=False) graph.plot (kind="bar",color='blue', fontsize = 15) plt.grid(b=True, which='both', color='white',linestyle='-') plt.axhline(y=1.2, xmin=2, xmax=0, linewidth=2, color = 'red', label = 'cc') plt.show (); 
Chronology of the development of the level of emissions:

Source: https://habr.com/ru/post/341130/
All Articles