Ethereum smart contract to calculate bonuses using fractional degrees

To begin with, that everyone knows. ICO is everywhere, everyone offers different projects, everyone sells tokens. And everyone has some kind of sales model with discounts, bonuses, terms, etc.
Oddly enough, the region is quite experimental, the model of bonuses is rather primitive. Simply, there are different volumes or time intervals and percentages in them. And why complicate things? And I still try. Experiment sake. New always attracts.

In addition to the issue of security, the second most important issue in the case of writing a smart contract is optimization. Each transaction consumes gas, and hence the air that is consumed during the processing of transactions. If the code is complex, it requires a lot of calculations - it will be very expensive for investors in ICO.

Now imagine that we want to make a smooth curve of bonuses depending on the amount of invested funds. And not just linear, but power.
Bonus = (Volume of Invest ^ 0.07) -1

Here is how it looks on the chart:
')


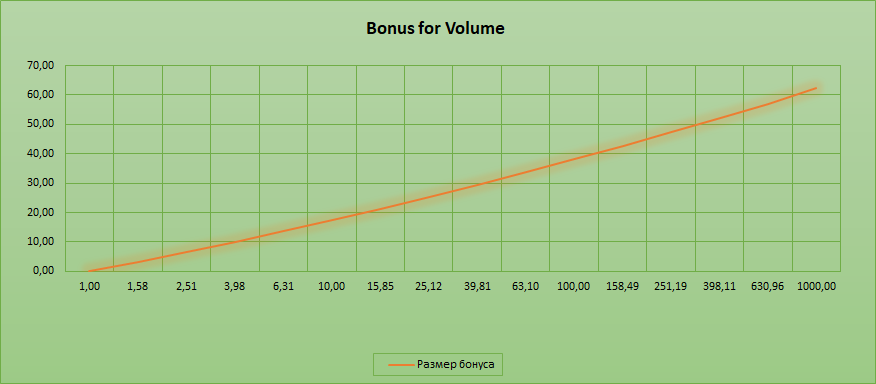
According to current statistics, the average investor invests around 5 ETH, so suppose that in the case of a volume less than 1 ETH the bonus will not be credited.

It will be necessary to calculate using only the uint type, since the float is still quite experimental and again quite expensive. And in this case we can use only multiplication, division, addition and subtraction.

Thus, we need to expand the exponentiation function into a series.

a ^ x = e ^ xlnx = 1 + xlna + (xlna) ^ 2/2! + (xlna) ^ 3/3! + ⋯ −∞ <x <∞

In turn, the logarithm of X must be calculated once, taking several key points in order to approximate it by a set of linear functions at different intervals.
Then take for example the first 4 members of the series.

Further assess the error by taking the normal calculator and the gas expended for calling the function.
You end up with something like this:

For example, calculated the values ​​for the approximation ln (1.07).

pragma solidity ^0.4.15; library SafeMath { function mul(uint256 a, uint256 b) internal constant returns (uint256) { uint256 c = a * b; assert(a == 0 || c / a == b); return c; } function div(uint256 a, uint256 b) internal constant returns (uint256) { // assert(b > 0); // Solidity automatically throws when dividing by 0 uint256 c = a / b; // assert(a == b * c + a % b); // There is no case in which this doesn't hold return c; } function sub(uint256 a, uint256 b) internal constant returns (uint256) { assert(b <= a); return a - b; } function add(uint256 a, uint256 b) internal constant returns (uint256) { uint256 c = a + b; assert(c >= a); return c; } } contract Simple { using SafeMath for uint256; uint256 m100=100000000; uint256 ln3= 109861228; uint256 ln10=230258512; uint256 ln20=299573231; uint256 ln30=340119743; uint256 ln50=391202307; uint256 ln100=460517025; uint256 ln200=529831743; uint256 ln500=621460819; uint256 ln1000=690775527; function test2(uint256 a){ test1(a); } function test1(uint256 a) constant returns (uint256 result) { uint256 lnbase; uint256 a0; if(a > m100.mul(1000)){ lnbase = ln1000; a0 = a.div(1000); }else if(a > m100.mul(500)){ lnbase=ln500; a0 = a.div(500); }else if(a > m100.mul(200)){ lnbase = ln200; a0 = a.div(200); }else if(a > m100.mul(100)){ lnbase = ln100; a0 = a.div(100); }else if(a > m100.mul(50)){ lnbase = ln50; a0 = a.div(50); }else if(a > m100.mul(30)){ lnbase = ln30; a0 = a.div(30); }else if(a > m100.mul(20)){ lnbase = ln20; a0 = a.div(20); }else if(a > m100.mul(10)){ lnbase = ln10; a0 = a.div(10); }else if(a > m100.mul(3)){ lnbase = ln3; a0 = a.div(3); }else if(a > m100){ lnbase = 0; a0 = a; }else{ return a; } uint256 x=a0.sub(m100).mul(m100).div(a0.add(m100)); uint256 y=x.add(x.mul(x).mul(x)/m100/m100/3).mul(2); y=lnbase.add(y); y=y.mul(7)/100; x=a.add(a.mul(y)/m100); x = x.add(a.mul(y).mul(y)/m100/m100/2); y = a.mul(y).mul(y).mul(y); x = x.add(y/m100/m100/m100/6); return (x); } } 

Rating:

9 ETH is multiplied by 10 ^ 8 and passed to the function:
900000000 gives 1048494787, i.e. 10.485 ETH (about 16% bonus)
on the calculator 9 ^ 1.07 = 10.496378550818314120261545161046 ETH
error: 0.001, i.e. 0.1%

Taking into account the transaction spent on translation, this error is quite comparable with the commission on the air. If you need more precision, you can certainly add 5 member series.

The cost of gas to call this function:
execution cost 9598 gas (cost only)

In the case of 1001 ETH, we get:
162102425800 in comparison with 1001 ^ 1.07 = 1623,54549 (i.e. a bonus of about 62%), this gives an accuracy of 1.0015, i.e. 0.15%
execution cost 6406 gas (Cost only

As you can see, the gas costs for the function are small (6-9k) considering that at the moment all ICOs recommend using 200k gas.
And at the same time, accuracy is within the limits of the commission for the average transaction.

If it seems to you that this is some kind of horse in a vacuum, then I would say that in the bonus system of the SINTEZ Platform project sintez.global the fractional degree and logarithm is used in the calculations.