Perfect shuffle

I have always been attracted to elementary algorithms with which you can create complex patterns. There is something fundamental in such algorithms. One of these algorithms is Perfect Shuffle. Let's look at its unusual properties, and also try to draw some impressive fractals using this algorithm.
Further there are a lot of pictures, gif-animations and some music.
Perfect Shuffle is known among gamblers-magicians. They call it Faro Shuffle. Recently, I also wanted to learn how to show card tricks. How do tricks begin? With the development of manual dexterity. After turning the pack of cards for a week, I mastered the basic ways of shuffling - “Riffle Shuffle”, “Faro Shuffle”, “Charlier Pass”. While practicing Faro Shuffle, I once arranged the deck so that all black suits are at the beginning of the deck, and the red suits are at the end. Having made Faro Shuffle several times, he paid attention to the unusual order of cards in the deck. Card postponed and sat down to program.
This algorithm changes the order of the elements in the array (shuffles the array). This algorithm is elementary:
')
1. We divide the array into two equal parts.
2. Elements from the first half of the array are placed in even positions. From the second - on the odd.
Clearly:
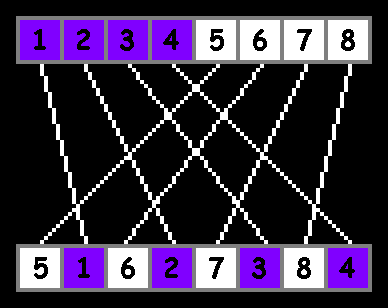
Even clearer:
Javascript:
function shuffle(array){ var half=array.length/2; // var temparray=[]; for(var i=0;i<half;i++){ temparray[i*2]=array[i+half]; // temparray[i*2+1]=array[i]; } return temparray; } var array=[1, 2, 3, 4, 5, 6, 7, 8]; array=shuffle(array); console.log(array); // [5, 1, 6, 2, 7, 3, 8, 4] Small lyrical digression
This option is the Perfect Shuffle gamblers called "in-shuffle". There is another option (“out-shuffle”) - elements from the first half of the array are placed in odd positions:
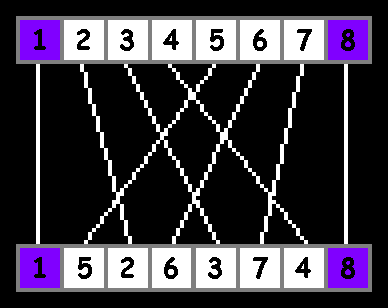
As you can see, the extreme elements remain in their positions, and the middle of the array is mixed with the same in-shuffle. Option out-shuffle is not considered further.
In addition, we do not consider the option when the number of elements in the array is odd - the last element in the array remains in its position.

As you can see, the extreme elements remain in their positions, and the middle of the array is mixed with the same in-shuffle. Option out-shuffle is not considered further.
In addition, we do not consider the option when the number of elements in the array is odd - the last element in the array remains in its position.
The algorithm has several noteworthy properties. If you mix the array several times - after n iterations, all elements will return to their original position! It is obvious. The algorithm is deterministic. For each next state of the array, there is only one unique previous state. The number of all possible states is limited by the length of the array. If we mix the array iteratively, sooner or later we will exhaust the possible states and go through the second circle. In fact, it will happen much earlier. The number of iterations required to return the array to its initial state is less (or equal) to the number of elements in the array. “Less or equal” - all that can be said about the number of iterations.
For an array of 12 elements, 12 iterations will suffice:
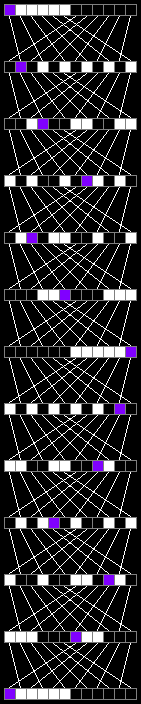
For an array of 14 elements, only 4 iterations will suffice:
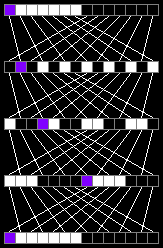
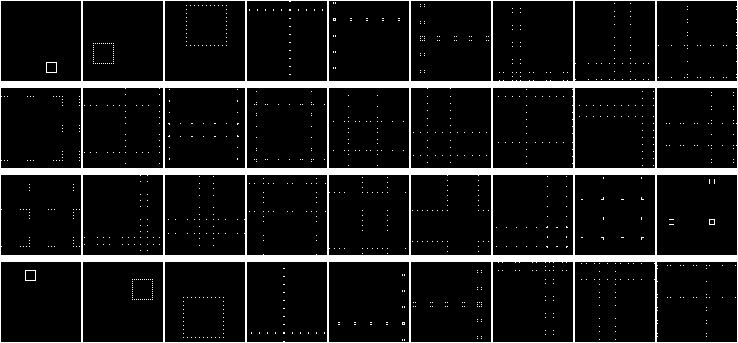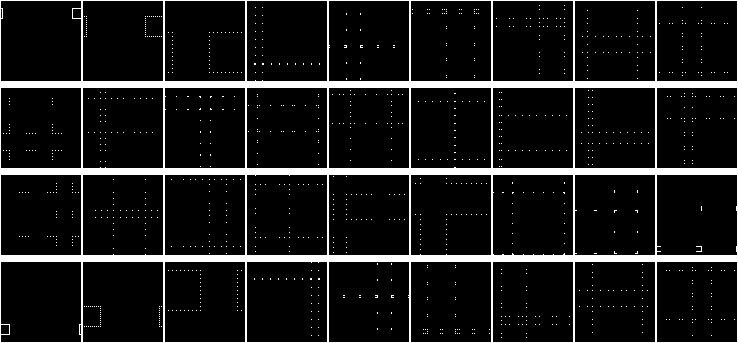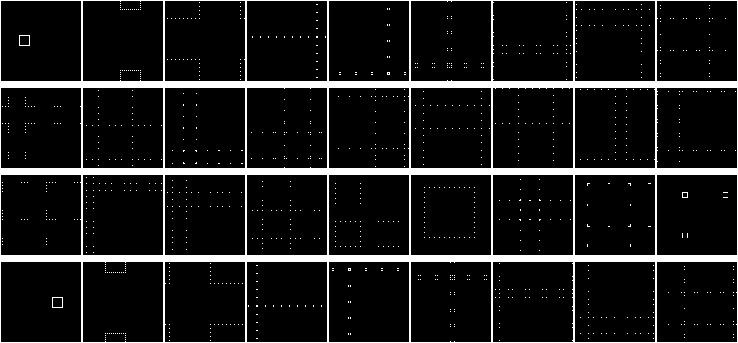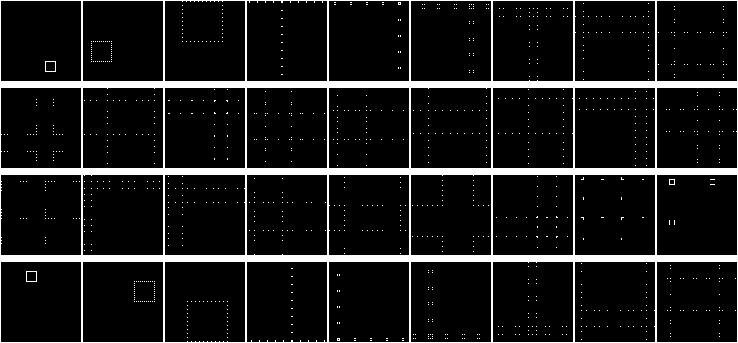
In the picture below (clickable) we mix arrays with lengths from 2 elements to 20:

(unshuffle)
The listed arrays are returned to their original state on
2, 4, 3, 6, 10, 12, 4, 8, 18, 6
iterations. Sequence A002326
Javascript
function a002326(n){ var a=1; var m=0; do{ a*=2; a%=2*n+1; m++; }while(a>1); return m; } for(var n=1;n<11;n++){ m=a002326(n); console.log(m); } Build a graph! On the graph on the X axis, we note the number of elements in the array (divided by 2). Y axis - the number of iterations. White dots denote the initial states of the arrays (the origin is the upper left corner):

Agree, the points on the chart are placed chaotically.
Another unusual property of Perfect Shuffle is that after a certain number of iterations, the order of the elements in the array may be reversed. Above in the picture we mixed an array of 12 elements. The order of the elements is reversed at the 6th iteration. Let's draw one more graph on which we will mark arrays with the reverse order of elements:

Again, the placement of points is no less chaotic.
It is very interesting to watch the movement of elements in the array! As elements from the first half of the array in the aggregate, and a specific (first) element in particular.
Fill the first half of the array with zeros, the second with units (hereafter, zeroes in the pictures are black pixels, ones are white). In the pictures below, each line ( X ) is an array state. Y - iteration.
Several arrays (142-150 elements):





Pictures are clickable
288 elements (144 * 2):

610 items:

For other array lengths
A small script that draws such wonderful pictures. We drive in the size of the array (half of the array), click "Draw".
By the way
He described one remarkable method of visualizing binary sequences in his first article.
An array of 142 elements at the 55th iteration looks like this:
0011001100011001100011001100011001100111001100111001100111001100111001100110001100110001100110001100110001100110011100110011100110011100110011
This sequence can be driven here and look at this array more clearly:

An array of 142 elements at the 55th iteration looks like this:
0011001100011001100011001100011001100111001100111001100111001100111001100110001100110001100110001100110001100110011100110011100110011100110011
This sequence can be driven here and look at this array more clearly:

A cellular automata as a wonderful look!









As you can see, here too we have total chaos. Let's observe a separate element and its trajectory in the array.
An array of 610 elements. Only the first item is filled:

In general, for a single element, it is not necessary to mix the entire array. The position of a specific element at the next iteration can be calculated by the formula:
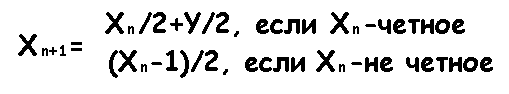
( Y is the length of the array)
The first arrays (with lengths from 2 to 22):
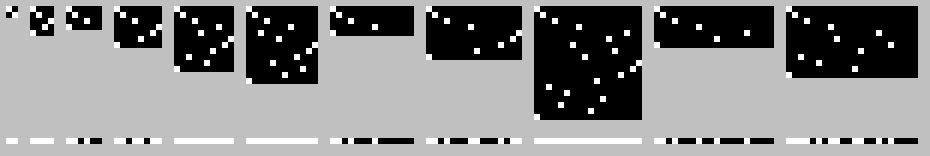
In the picture above: in the upper part of the picture is the array and the position of the element at each iteration, in the lower part of the line - all possible positions of the element. As you can see, the trajectory of the element inside the array is also not obvious. To finally verify this - from these lines we will make one more graph, adding them up as follows:
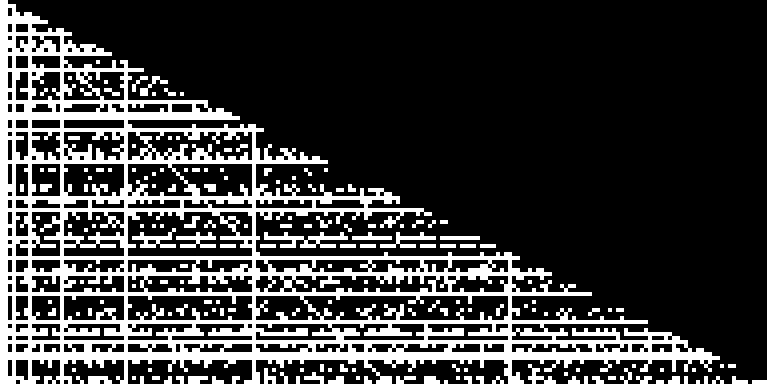
Clickable
Black pixels are those positions in the array that the first element does not fall into when mixed.
We could stop at this, but we will go even further! Observe the movement of all elements in the array. For this we go to the matrices.
But before moving on to the mixing of matrices, I will show two more foci with arrays.
In the second half of the array, we reverse the order of the elements (at each iteration):

In the second half we invert the elements:

These two operations will still be useful to us.
Let's go to the matrices!
Fill in the matrix, in the first row - the first element, in the second - the second, etc. In other words, draw a diagonal:

Shuffle the columns in the matrix using Perfect Shuffle. So we can see where all the elements fall after mixing. Matrix 80x80:
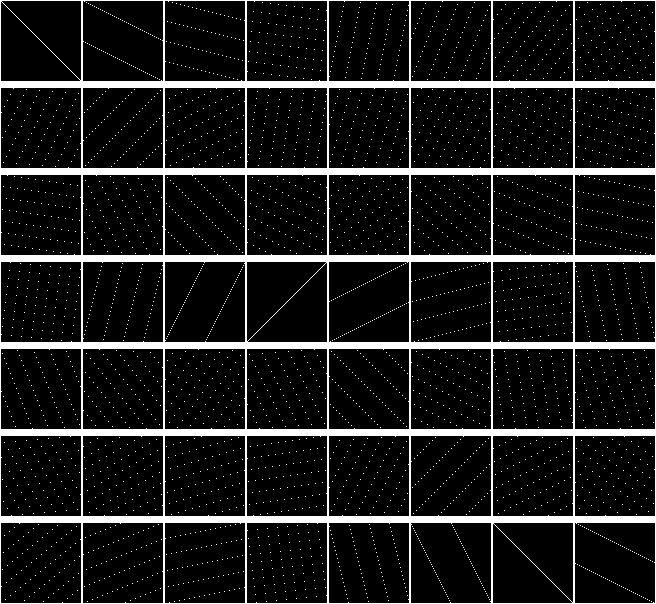
There is clearly lacking another diagonal:

A very curious moire is obtained. Matrix 242x242 from 27 to 35 iteration:

Well, if you have already started to mix columns in the matrix using Perfect Shuffle - why not mix the lines?
We modify our function a bit:
A function that mixes rows and columns in a matrix.
function shufflecr(array){ var half=array.length/2; var temparray=[]; for(var x=0;x<half;x++){ temparray[x*2]=[]; temparray[x*2+1]=[]; for(var y=0;y<half;y++){ temparray[x*2][y*2]=array[x+half][y+half]; temparray[x*2+1][y*2]=array[x][y+half]; temparray[x*2][y*2+1]=array[x+half][y]; temparray[x*2+1][y*2+1]=array[x][y]; } } return temparray; } We divide the matrix into 4 parts. Mix the columns. Mix the strings. We get a new matrix. Clearly:

The diagonals shuffle are pretty boring:

It may even seem that in the function somewhere an error and the matrix is not mixed. Shift the diagonals one pixel to the right:

Wonderful. The function works, the matrix is mixed. True, again quite boring. Let's try to fill the matrix with some kind of pattern. In a random place draw a square:

The size of the matrix 80x80 was not chosen by chance. When mixing an array of 80 elements in length, at the 27th iteration, the order of the elements is reversed.
Let's move this square!
Here you can see one very interesting property, but even better this property is visible if you draw a circle:

Pay attention to edge effects. Our matrix collapses into a torus! This is clearly seen in the second iteration.
Move:

By the way
Perfect Shuffle has a curious connection with trigonometry.
Above, we mixed the array and got some great pictures. One of them (144 * 2):

We also write it in the matrix and mix:

Or even so. Take the original pattern:

And leave pixels on it with coordinates x * 4 + i, y * 4 + j. For i = 2, j = 2:

Remove empty columns and rows:

For other i and j (actually made perfect unshuffle - divided the matrix into 16 parts):

Familiar patterns! Similar patterns can be drawn using the z = sin (n * x / y) and z = sin (n * x * y) trigonometric functions.
Graph of the function z = sin (3 * x * y). If z> = 0 - white pixel. If z <0 is black:

z = sin (13 * x * y):

Above, we mixed the array and got some great pictures. One of them (144 * 2):

We also write it in the matrix and mix:

Or even so. Take the original pattern:

And leave pixels on it with coordinates x * 4 + i, y * 4 + j. For i = 2, j = 2:

Remove empty columns and rows:

For other i and j (actually made perfect unshuffle - divided the matrix into 16 parts):

Familiar patterns! Similar patterns can be drawn using the z = sin (n * x / y) and z = sin (n * x * y) trigonometric functions.
Graph of the function z = sin (3 * x * y). If z> = 0 - white pixel. If z <0 is black:

z = sin (13 * x * y):

One of the interesting patterns:

We can make a fill to highlight closed areas:

By the way
The old, kind and well-loved donkey (Internet Explorer) does not use any clever image reduction algorithms. It simply takes and throws out every nth column and nth row of pixels from the image. If we don’t throw them away, but put them into separate matrices, we get the process (unshuffle) of the inverse Perfect Shuffle (with n = 2).
Actually, it's pretty cool! We can take this pattern:

And a little squeeze it a donkey:
Got a familiar pattern.
You can play with other templates:

Squeezed a donkey:
Actually, it's pretty cool! We can take this pattern:

And a little squeeze it a donkey:

Got a familiar pattern.
You can play with other templates:

Squeezed a donkey:

Recall the tricks (reversing the order of elements and invert).
Changing the order of the elements gives very interesting patterns! One of them:

With fill:

Other patterns are no less interesting, but we will not dwell on them. It is much more interesting to watch the inversion.
For this experiment, we have enough of an empty matrix. Divide it into 4 parts. Two of them are inverted. Stir. At the first iteration, nothing unusual:

But further curious patterns appear:

To figure out where these patterns come from, let us go back to the arrays again. Before that, we used matrices and arrays of fixed length. Let's try to change the approach a little - we will gradually increase the length:
1. Create an array of n elements.
2. Make a copy of it.
3. Shuffle the copy with the original using Perfect Shuffle. Got an array of n * 2 elements.
4. Return to step 2.
We will invert the copy each time.
Let's start with an array of two elements - 1 and 0
10 - source array
10, 01 - array and inverted copy
0110 - mixed
0110, 1001 - array and inverted copy
10010110
10010110, 01101001
0110100110010110
… etc.
Received Morse-Thue sequence ( A010060 ) - the simplest fractal!
And back to the matrices. This is where pure art begins. Before that, we divided the matrix into 4 parts and mixed these parts. Let's try to copy the matrix, perform some elementary actions on copies and mix the original with copies.
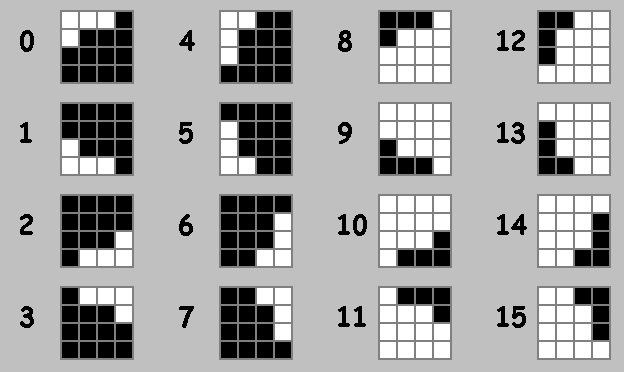
With matrices we can produce 15 elementary actions. Action 0 - no change matrix. Steps 1-7 are different ways to rotate the matrix. Steps 8-15 are invert. Clearly:
As an example, we perform 0, 0, 7, 7 actions on copies. Step 7 - rotate the matrix by 90 °.
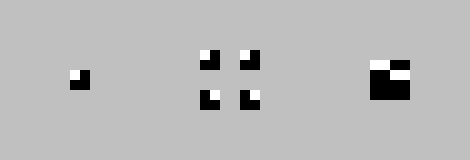
Next iteration:
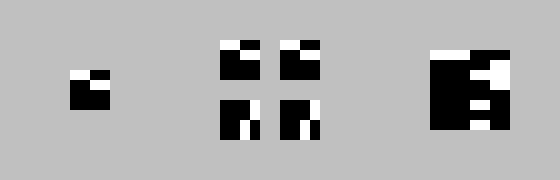
... the eighth iteration:

A very unusual fractal turned out.
By the way
A similar way to draw fractals came up as a student. Perform the same actions, but without mixing the matrix using Perfect Shuffle.
Actions 0, 0, 7, 7. First iteration:

Second iteration:
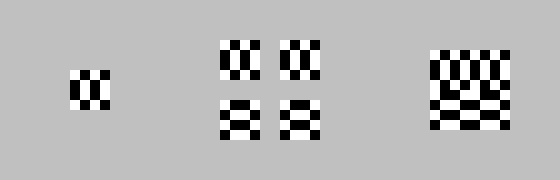
Eighth:

And now two focus.
We put on top of the copy of the image with transparent white pixels, rotate the copy by 90 °:

The copy is rotated vertically:

Actions 0, 0, 7, 7. First iteration:

Second iteration:
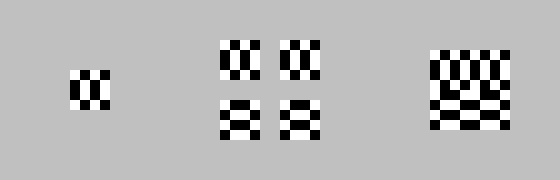
Eighth:

And now two focus.
We put on top of the copy of the image with transparent white pixels, rotate the copy by 90 °:

The copy is rotated vertically:

By combining the listed actions, you can draw 16 ^ 4 = 65536 fractals. Some of them:
Drawn in 6 iterations. Pictures are clickable (8 iterations).





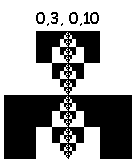

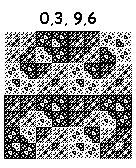


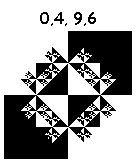














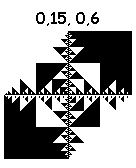






But these pull on the masterpiece:
15, 5, 9, 5:

3, 5, 9, 5:

13, 7, 11, 11:

0, 0, 7, 13:

1, 1, 4, 14:

Other fractals can be drawn here.
These are the "card tricks" turned out. I think this can be temporarily stopped (you can mix three-dimensional matrix, but more on that another time).
For those who read to this place
I tried to write a generator of melodies based on a genetic algorithm. Each tune consists of note-genes. If the genes of descendants mix randomly - it turns out cacophony. But if you mix them using Perfect Shuffle, you get curious melodies. One of them:
By the way





Source: https://habr.com/ru/post/340964/
All Articles