Algorithms for building a path for an unmanned vehicle. Yandex lecture
Yandex has been developing an unmanned vehicle for some time. Here is one of the first technical lectures on this topic. In the direction of unmanned vehicles, Yandex employees work in different cities, including Minsk. The author of the lecture, Roman Udovichenko, is from Minsk - he leads the traffic situation handling team. In September, J.Subbotnik, Roman spoke about one of the big challenges facing his group.
- My name is Roma Udovichenko, I work at Yandex in Minsk as the head of the traffic situation management team in the direction of unmanned vehicles. Today I will talk about a very small, but important part of our work - algorithms for constructing a path for an unmanned vehicle.
First, I want to understand what needs to be done to teach the car to drive independently - provided that we have hung it with sensors, hung cameras, radar and anything on it. We can do everything, it remains to write a code of assumptions.
')
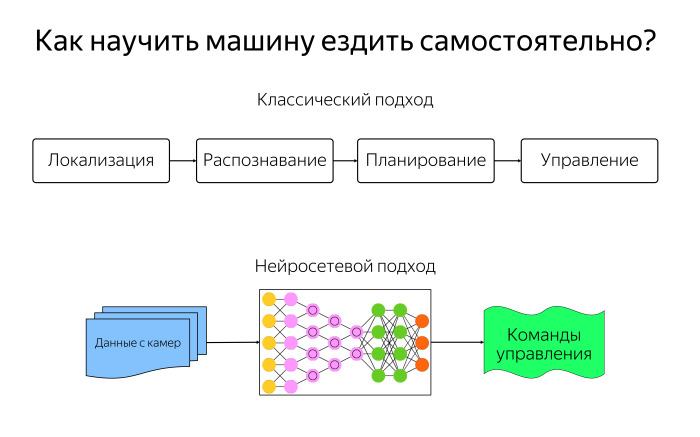
We can use the classic approach of robotics. We divide our task of independent movement into four modules. The localization module is responsible for ensuring that the machine understands where it is located. Recognition module - for being around the car. Planning module has information about what is around, and knowing where you want to come, builds a route. The control module tells you how to travel along the route in order to arrive and fulfill this trajectory.
And we can apply the modern technology of neural networks and say that we will not program anything explicitly. Let's just submit a picture from the cameras to the neural network, after having trained it on any human movements. We will train in what situations where you need to turn the steering wheel, brake, gas, take a lot of data, make a big neural network, and according to the idea it should behave well after that.
There is a lot of work being done in this direction, but in practice it seems that you still need too much data, you need too much neural network to follow everything successfully for a person in different situations. Therefore, today we will talk about the classical approach, in particular - about planning a path, building a trajectory along which we will travel.
Why is planning a path a difficult task that you cannot do in a week and go on doing something interesting? The car generally has a number of fairly significant limitations. This is not a ball in space that can roll in any direction and conditionally instantly stop and slow down. The car has the current direction, the angle of rotation of the wheels, and it can not just be two meters to the left of the current location, it is very difficult. It can go approximately forward, turning at some angle, but nevertheless, the movement is very limited. And the trajectory that we build is subject to the constraints that follow from the kinematics. For example, we can not instantly accelerate and even instantly increase our acceleration.

Today we will look at such varieties of path construction algorithms that a car can drive well. In particular, more or less classical algorithms on graphs, optimization methods using continuous mathematical optimizations, stochastic algorithms that consider random behavior, and specialized methods that solve a very particular problem, but solve it very well — better than in the general case.
The first thing to begin with is the algorithms on the graphs. The first question we need to answer in order to understand which algorithms can be applied is how to build a graph in general? Here is the car, we can understand where it stands, but in reality there is no graph, the vertices of the edges on the road are not drawn. We need to think of this graph ourselves. The first thing we can do: we divide the whole space into cells, consider small cells and say that there is our entire surface of the earth, divided into 25 cells by 25 or 50 by 50 cm. Then we connect adjacent cells with edges and we will look for a path on them. It will be quite far from the path that the car can travel, but it will give some approximation. And we will have such vertices in two-dimensional space.
We can complicate our space by adding the current angle of rotation of the machine. We will already have cells not just x and y, but the current orientation of the machine in the directions north, south, west and east, also somehow discretized. In addition to the direction, we can take into account a lot of things: current machine speed, current acceleration, current tangential acceleration, normal. All this is important to consider. But the more we complicate our space, the more complex our graph becomes.
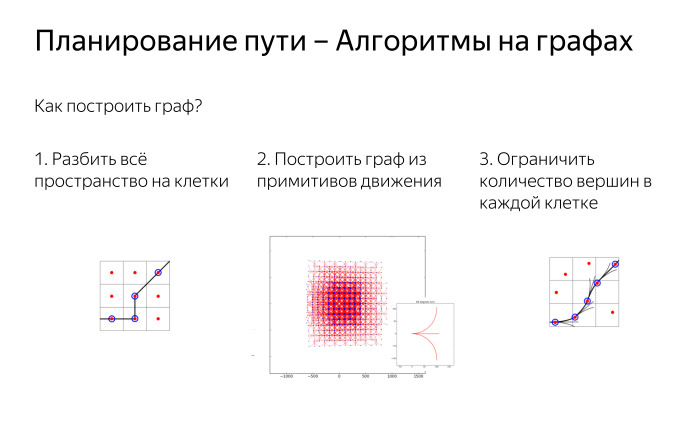
In addition to dividing the space into cells, we can say that we are able to move in small steps in the form of primitives. For example, drive 50 cm forward or drive 50 cm forward and turn left or drive 50 cm forward and turn right. And with such primitives we can pave all our space. We do not have cells in an explicit form, but if these small steps are fairly well coordinated with each other, then we have a regular grid that covers the space well and accurately.
Suppose we consider primitives that do not fit so well together - for example, let's say that turning to the left occurs at an angle of 89 degrees, and turning right at an angle of 90 degrees. Then we already have the same number of vertices, as in the previous picture, will occupy a significantly smaller area of space, since they do not fit well with each other and the density of points will be very high, and we will not be able to cover the space far.
We can combine these two approaches and say that we consider the primitive movement at any angle, drive forward, drive forward and turn 10 degrees, 15 degrees, whatever. At the same time, we still divide the space into cells and say that in one cell there cannot be more than 1, 2, ..., k vertices.
When we consider the next vertex in the graph in the process of using some kind of algorithm, we say that there is a new vertex in the cell, we process it accordingly. If it then turns out that we want to get to the specified cell at another vertex, then we will not consider it. This makes it impossible for us to build a more optimal route than if we used all the vertices. But this can significantly increase the speed and efficiency.
We have a graph, we want to apply some algorithm on it. There is an A * algorithm.

There is a Dijkstra algorithm, which is slightly more well-known than the A * algorithm, and which bypasses all the vertices in the graph in ascending order of distance from the starting vertex. Pulls them from some queue with priority in order of increasing distance. In the upper figure we see that if the starting pink top is at the beginning, then we will gradually consider all the vertices on the radius increasing from the starting one, and eventually we will arrive at the top, which is our goal.
To search more efficiently, we will consider vertices not only by increasing the distance from the start, but also add to this distance a certain heuristic estimate of how much we have to go to the end. The logic is very clear: we are not just saying that we are now standing at some peak, and therefore we are considering the next peak at some distance from the start. We are adding to this parameter some function that allows us to evaluate more promising peaks, from which, most likely, we are close to the finish line. We do not know how much to actually go from each peak to the finish, because if we knew, we would not have to look for a way either. But we can somehow evaluate it and get the picture in the lower figure. We will evaluate the vertices that somehow go in the direction of our goal, and consider a significantly smaller number of vertices than in the Dijkstra algorithm. You can tell a lot about this, but in general the idea is that for the correct operation of the algorithm, it is necessary that our heuristic, the function of estimating the distance to the final vertex, never exceeds the actual distance that we have to go. Only in this case the correct operation of the algorithm is guaranteed.

You can use different approaches as heuristic functions. This is the difficulty of applying the algorithm A *. The better heuristics you can pick up, the better it will go towards the goal, the fewer peaks it will consider and the faster it will work.
The simplest thing we can do is consider the distance to the target straight. Obviously, we cannot reach the end point faster than if we just go straight to it as a tank.
A more complex and more efficient heuristic is the distance, taking into account our kinematic constraints, but without taking into account the obstacles. Suppose there is nothing in the world, only we and the target, but the machine cannot instantly move left or right; it travels according to its laws, according to the physical model of the machine. Since there are no obstacles, we can calculate in advance the distance to the target from various places in which we can be, and use this as a heuristic function.
We can do the opposite: say that there is an obstacle, but, let's say, the car can move forward, back, left, right, somehow, quickly accelerate and quickly brake. We construct our distance taking into account the obstacles that we see. Again, we get an estimate that is lower than the actual distance we have to go.
And finally, of all the heuristics we can consider the maximum. Since each of them does not exceed our actual distance, the maximum of them, too, will not exceed the actual distance and the algorithm will work well.

What do we get? Algorithm A * allows us to find the optimal path that leads us to the goal, skirting obstacles. But if we have a space of small dimension, we consider only x, y, the orientation of the machine, and the fact that it cannot immediately accelerate, which means that all these restrictions will be taken into account. If we add a large number of parameters to our graph, it will be in a space of very high dimension. We will have 7, 8, 10 dimensional space, we will have time to consider small pieces of this space and will not be able to build a sufficiently distant route due to the very high variability of the parameters. In some situations, A * is difficult to apply, but somewhere it shows itself quite well.
The second option is optimization methods based not on a discrete, but on a more continuous approach.


The statement of the problem may be as follows: consider the trajectory of our position in time, x and y, depending on time t, that is, we will understand at what point we want to be at time t. We can determine the angle of the tangent through the arctangent of the derivatives, we can say that the optimal path in this case is the trajectory that minimizes the functional, which is the integral of time ahead of some function of the trajectory. The function of the trajectory here in some way finishes us for sharp turns, sharp accelerations, being close to obstacles, etc. Then, if we add along all our trajectories all these penalties that we invent ourselves, and try to minimize it with a standard mathematical apparatus, not related to cars in general and unmanned vehicles in particular, we will solve the problem in some general form.

What examples of penalties can we consider? For example, we can say that we do not want to drive close to obstacles, take this into account with some weight, do not want our speed to be much higher or lower than the desired speed, which we have determined for ourselves. We can penalize ourselves for the second derivative, which is an acceleration, because we do not want the car to sharply sink to the floor and slow down sharply.
We can consider the third derivative, which is a jerk, that is, we do not want the acceleration to change dramatically enough. By the way, it is precisely from the sudden change in the acceleration that people are swayed during the ride. If the acceleration is fixed and the car just accelerates all the time, then, as studies show, people are not swayed. The vestibular apparatus of the person catches and does not always respond well, if it then accelerates, it slows down. We may not want to make sharp turns, limit our angle. And there are additional restrictions that say that the car cannot physically accelerate faster than some kind of acceleration. If we all take this into account in some way, then we will be able to solve the problem using an abstract function minimization algorithm and get some result.
Separately, I want to talk about calculating distances, because in most optimization methods they like to work with smooth functions that are well differentiated and smooth. Then everything works well there. And our car is an object of rather complex shape, and the obstacles that we go around are also objects of cunning forms. Therefore, it is necessary to make some kind of simplification. For example, we can say that a car is not something complicated, but simply five circles that go back and forth.
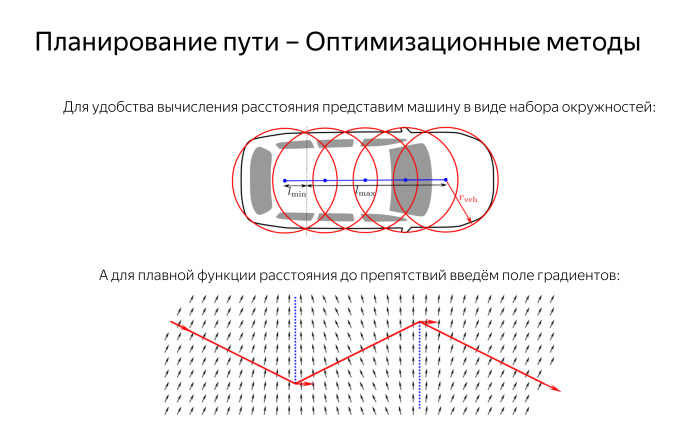
It will be like the truth, though not completely, but the approximation is good. And from the circles it is very easy to count the distances to anything, and it is very easy to check the circle for intersections with other geometric primitives. If the distance to the center is less than the radius, then here is the intersection, otherwise everything is fine.
What you need to smoothly change the distance? Our Euclidean distance to nonconvex polygons does not possess the properties we need and is poorly differentiable in places where this nonconvexity occurs. Therefore, we can construct such a pseudo-distance along the gradient field to our broken line; it is here marked in red and represents an obstacle. We can quite easily introduce the field of distances from each point to this broken line, which is directed towards the broken line and has the necessary differentiability properties - even if it is not strictly shortest. If we do all this, we will be able to build a smooth, beautiful, and neat path.

The advantages of such methods, we refer to the fact that you get a good trajectory and control space continuously. We can go on it, all restrictions in one degree or another are respected. But unfortunately, most optimization methods or even almost all somehow suffer from local minima, where their attempts to optimize something get stuck and do not find a sufficiently good solution. It is very difficult to formulate everything in the form of mathematical differentiable functions, this also does not always work.
However, there is a solution. We can apply algorithms that work in some random way, but they allow us to build some approximate route fairly quickly and conveniently. For example, we will build our graph, which is a tree, in an iterative way. At first, we will not divide anything into cells, we will not build any primitives. We just take the simulator of our car, which in general is able to simulate the movement, the most similar to how the car goes for real. And take the starting point. After that, iteratively choose a random point in space. And - we will find the node nearest to it in the current constructed tree. Construct an edge in the direction of this point using the simulation of travel in this direction.
It turns out that every time we drive from our constructed tree to a random direction and we can do vertices in this tree in a space of any dimension, that is, at each vertex we must take into account the current direction of the car, current speed, acceleration, all angles that are important to us. And then, when we take a new point, we take the vertex nearest to this point. We will drive with the help of some kind of simulation, for example, 5 meters in the direction of this point. Then take another point and drive in her direction.
What does this give us? Every time we explore space, but very aggressively. We are not looking for optimal ways to drive around an obstacle. We just go in different directions, but every time we do it from the most explored part of our space to that unknown side.

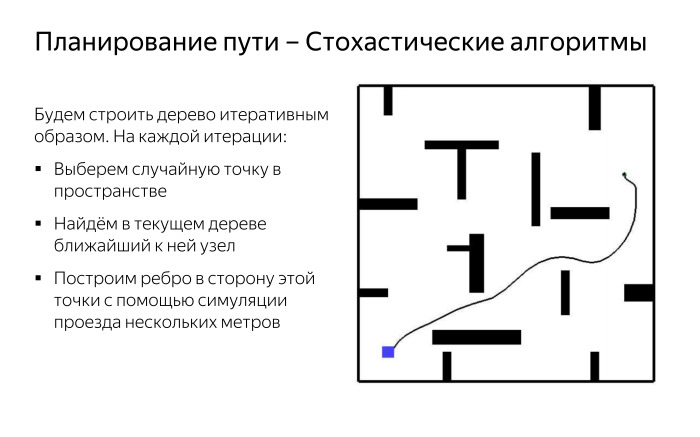
Due to this, we quickly get a picture where “tentacles” grow in different directions, which somehow cover our space. Perhaps suboptimally, but rather quickly. The square in the corner is our starting position. Then we can get some way to the goal, which may not be entirely optimal and elegant, but it is obtained in a fairly quick way.

And it turns out, the advantages are that we work very quickly in multidimensional spaces. Since we get the paths through fair simulation, we can almost directly transfer them to the control unit. Disadvantages? We have no guarantees that our points will be chosen well enough. Solutions can turn out pretty curves and not always optimal.
Specialized methods. When the car drives in the city, we have no abstract points A and B and an unstructured environment with random obstacles. In our city, everything is more or less clear: there are concrete lanes and the movement of our car almost always lies in the fact that we drive approximately in the center of the lane, sometimes we shift to the left or to the right to go around the obstacle, sometimes we rebuild to turn according to the rules of the road wherever needed. At the intersections from one lane to another we are rebuilding.

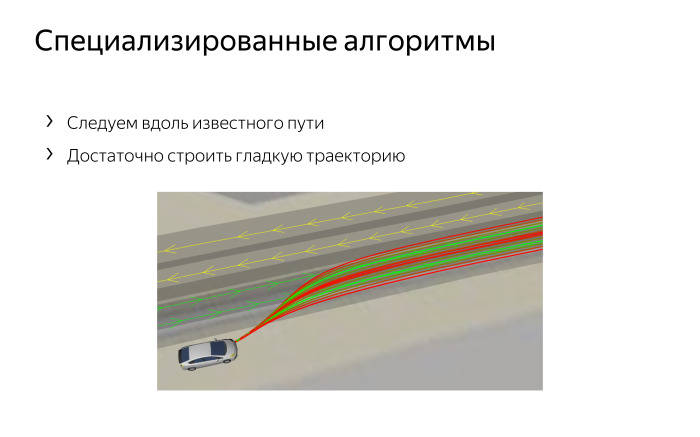
We do not always need these tricky trees to park or make difficult maneuvers. , , - , - -. , . , , , , . . , .

, . , , . , , , , . . , - , , . .
, , . .

, , . , , , . , . . , . , — , , . .

— , . — . . , — . Thank you very much.
We just take the current position of the car, look at the path that we would like to go, and smoothly turn on this path, taxi on it. It turns out quite simple. But moving in the city due to the fact that you need to follow the rules of the road.
- My name is Roma Udovichenko, I work at Yandex in Minsk as the head of the traffic situation management team in the direction of unmanned vehicles. Today I will talk about a very small, but important part of our work - algorithms for constructing a path for an unmanned vehicle.
First, I want to understand what needs to be done to teach the car to drive independently - provided that we have hung it with sensors, hung cameras, radar and anything on it. We can do everything, it remains to write a code of assumptions.
')

We can use the classic approach of robotics. We divide our task of independent movement into four modules. The localization module is responsible for ensuring that the machine understands where it is located. Recognition module - for being around the car. Planning module has information about what is around, and knowing where you want to come, builds a route. The control module tells you how to travel along the route in order to arrive and fulfill this trajectory.
And we can apply the modern technology of neural networks and say that we will not program anything explicitly. Let's just submit a picture from the cameras to the neural network, after having trained it on any human movements. We will train in what situations where you need to turn the steering wheel, brake, gas, take a lot of data, make a big neural network, and according to the idea it should behave well after that.
There is a lot of work being done in this direction, but in practice it seems that you still need too much data, you need too much neural network to follow everything successfully for a person in different situations. Therefore, today we will talk about the classical approach, in particular - about planning a path, building a trajectory along which we will travel.
Why is planning a path a difficult task that you cannot do in a week and go on doing something interesting? The car generally has a number of fairly significant limitations. This is not a ball in space that can roll in any direction and conditionally instantly stop and slow down. The car has the current direction, the angle of rotation of the wheels, and it can not just be two meters to the left of the current location, it is very difficult. It can go approximately forward, turning at some angle, but nevertheless, the movement is very limited. And the trajectory that we build is subject to the constraints that follow from the kinematics. For example, we can not instantly accelerate and even instantly increase our acceleration.

Today we will look at such varieties of path construction algorithms that a car can drive well. In particular, more or less classical algorithms on graphs, optimization methods using continuous mathematical optimizations, stochastic algorithms that consider random behavior, and specialized methods that solve a very particular problem, but solve it very well — better than in the general case.
The first thing to begin with is the algorithms on the graphs. The first question we need to answer in order to understand which algorithms can be applied is how to build a graph in general? Here is the car, we can understand where it stands, but in reality there is no graph, the vertices of the edges on the road are not drawn. We need to think of this graph ourselves. The first thing we can do: we divide the whole space into cells, consider small cells and say that there is our entire surface of the earth, divided into 25 cells by 25 or 50 by 50 cm. Then we connect adjacent cells with edges and we will look for a path on them. It will be quite far from the path that the car can travel, but it will give some approximation. And we will have such vertices in two-dimensional space.
We can complicate our space by adding the current angle of rotation of the machine. We will already have cells not just x and y, but the current orientation of the machine in the directions north, south, west and east, also somehow discretized. In addition to the direction, we can take into account a lot of things: current machine speed, current acceleration, current tangential acceleration, normal. All this is important to consider. But the more we complicate our space, the more complex our graph becomes.

In addition to dividing the space into cells, we can say that we are able to move in small steps in the form of primitives. For example, drive 50 cm forward or drive 50 cm forward and turn left or drive 50 cm forward and turn right. And with such primitives we can pave all our space. We do not have cells in an explicit form, but if these small steps are fairly well coordinated with each other, then we have a regular grid that covers the space well and accurately.
Suppose we consider primitives that do not fit so well together - for example, let's say that turning to the left occurs at an angle of 89 degrees, and turning right at an angle of 90 degrees. Then we already have the same number of vertices, as in the previous picture, will occupy a significantly smaller area of space, since they do not fit well with each other and the density of points will be very high, and we will not be able to cover the space far.
We can combine these two approaches and say that we consider the primitive movement at any angle, drive forward, drive forward and turn 10 degrees, 15 degrees, whatever. At the same time, we still divide the space into cells and say that in one cell there cannot be more than 1, 2, ..., k vertices.
When we consider the next vertex in the graph in the process of using some kind of algorithm, we say that there is a new vertex in the cell, we process it accordingly. If it then turns out that we want to get to the specified cell at another vertex, then we will not consider it. This makes it impossible for us to build a more optimal route than if we used all the vertices. But this can significantly increase the speed and efficiency.
We have a graph, we want to apply some algorithm on it. There is an A * algorithm.

There is a Dijkstra algorithm, which is slightly more well-known than the A * algorithm, and which bypasses all the vertices in the graph in ascending order of distance from the starting vertex. Pulls them from some queue with priority in order of increasing distance. In the upper figure we see that if the starting pink top is at the beginning, then we will gradually consider all the vertices on the radius increasing from the starting one, and eventually we will arrive at the top, which is our goal.
To search more efficiently, we will consider vertices not only by increasing the distance from the start, but also add to this distance a certain heuristic estimate of how much we have to go to the end. The logic is very clear: we are not just saying that we are now standing at some peak, and therefore we are considering the next peak at some distance from the start. We are adding to this parameter some function that allows us to evaluate more promising peaks, from which, most likely, we are close to the finish line. We do not know how much to actually go from each peak to the finish, because if we knew, we would not have to look for a way either. But we can somehow evaluate it and get the picture in the lower figure. We will evaluate the vertices that somehow go in the direction of our goal, and consider a significantly smaller number of vertices than in the Dijkstra algorithm. You can tell a lot about this, but in general the idea is that for the correct operation of the algorithm, it is necessary that our heuristic, the function of estimating the distance to the final vertex, never exceeds the actual distance that we have to go. Only in this case the correct operation of the algorithm is guaranteed.

You can use different approaches as heuristic functions. This is the difficulty of applying the algorithm A *. The better heuristics you can pick up, the better it will go towards the goal, the fewer peaks it will consider and the faster it will work.
The simplest thing we can do is consider the distance to the target straight. Obviously, we cannot reach the end point faster than if we just go straight to it as a tank.
A more complex and more efficient heuristic is the distance, taking into account our kinematic constraints, but without taking into account the obstacles. Suppose there is nothing in the world, only we and the target, but the machine cannot instantly move left or right; it travels according to its laws, according to the physical model of the machine. Since there are no obstacles, we can calculate in advance the distance to the target from various places in which we can be, and use this as a heuristic function.
We can do the opposite: say that there is an obstacle, but, let's say, the car can move forward, back, left, right, somehow, quickly accelerate and quickly brake. We construct our distance taking into account the obstacles that we see. Again, we get an estimate that is lower than the actual distance we have to go.
And finally, of all the heuristics we can consider the maximum. Since each of them does not exceed our actual distance, the maximum of them, too, will not exceed the actual distance and the algorithm will work well.

What do we get? Algorithm A * allows us to find the optimal path that leads us to the goal, skirting obstacles. But if we have a space of small dimension, we consider only x, y, the orientation of the machine, and the fact that it cannot immediately accelerate, which means that all these restrictions will be taken into account. If we add a large number of parameters to our graph, it will be in a space of very high dimension. We will have 7, 8, 10 dimensional space, we will have time to consider small pieces of this space and will not be able to build a sufficiently distant route due to the very high variability of the parameters. In some situations, A * is difficult to apply, but somewhere it shows itself quite well.
The second option is optimization methods based not on a discrete, but on a more continuous approach.


The statement of the problem may be as follows: consider the trajectory of our position in time, x and y, depending on time t, that is, we will understand at what point we want to be at time t. We can determine the angle of the tangent through the arctangent of the derivatives, we can say that the optimal path in this case is the trajectory that minimizes the functional, which is the integral of time ahead of some function of the trajectory. The function of the trajectory here in some way finishes us for sharp turns, sharp accelerations, being close to obstacles, etc. Then, if we add along all our trajectories all these penalties that we invent ourselves, and try to minimize it with a standard mathematical apparatus, not related to cars in general and unmanned vehicles in particular, we will solve the problem in some general form.

What examples of penalties can we consider? For example, we can say that we do not want to drive close to obstacles, take this into account with some weight, do not want our speed to be much higher or lower than the desired speed, which we have determined for ourselves. We can penalize ourselves for the second derivative, which is an acceleration, because we do not want the car to sharply sink to the floor and slow down sharply.
We can consider the third derivative, which is a jerk, that is, we do not want the acceleration to change dramatically enough. By the way, it is precisely from the sudden change in the acceleration that people are swayed during the ride. If the acceleration is fixed and the car just accelerates all the time, then, as studies show, people are not swayed. The vestibular apparatus of the person catches and does not always respond well, if it then accelerates, it slows down. We may not want to make sharp turns, limit our angle. And there are additional restrictions that say that the car cannot physically accelerate faster than some kind of acceleration. If we all take this into account in some way, then we will be able to solve the problem using an abstract function minimization algorithm and get some result.
Separately, I want to talk about calculating distances, because in most optimization methods they like to work with smooth functions that are well differentiated and smooth. Then everything works well there. And our car is an object of rather complex shape, and the obstacles that we go around are also objects of cunning forms. Therefore, it is necessary to make some kind of simplification. For example, we can say that a car is not something complicated, but simply five circles that go back and forth.

It will be like the truth, though not completely, but the approximation is good. And from the circles it is very easy to count the distances to anything, and it is very easy to check the circle for intersections with other geometric primitives. If the distance to the center is less than the radius, then here is the intersection, otherwise everything is fine.
What you need to smoothly change the distance? Our Euclidean distance to nonconvex polygons does not possess the properties we need and is poorly differentiable in places where this nonconvexity occurs. Therefore, we can construct such a pseudo-distance along the gradient field to our broken line; it is here marked in red and represents an obstacle. We can quite easily introduce the field of distances from each point to this broken line, which is directed towards the broken line and has the necessary differentiability properties - even if it is not strictly shortest. If we do all this, we will be able to build a smooth, beautiful, and neat path.

The advantages of such methods, we refer to the fact that you get a good trajectory and control space continuously. We can go on it, all restrictions in one degree or another are respected. But unfortunately, most optimization methods or even almost all somehow suffer from local minima, where their attempts to optimize something get stuck and do not find a sufficiently good solution. It is very difficult to formulate everything in the form of mathematical differentiable functions, this also does not always work.
However, there is a solution. We can apply algorithms that work in some random way, but they allow us to build some approximate route fairly quickly and conveniently. For example, we will build our graph, which is a tree, in an iterative way. At first, we will not divide anything into cells, we will not build any primitives. We just take the simulator of our car, which in general is able to simulate the movement, the most similar to how the car goes for real. And take the starting point. After that, iteratively choose a random point in space. And - we will find the node nearest to it in the current constructed tree. Construct an edge in the direction of this point using the simulation of travel in this direction.
It turns out that every time we drive from our constructed tree to a random direction and we can do vertices in this tree in a space of any dimension, that is, at each vertex we must take into account the current direction of the car, current speed, acceleration, all angles that are important to us. And then, when we take a new point, we take the vertex nearest to this point. We will drive with the help of some kind of simulation, for example, 5 meters in the direction of this point. Then take another point and drive in her direction.
What does this give us? Every time we explore space, but very aggressively. We are not looking for optimal ways to drive around an obstacle. We just go in different directions, but every time we do it from the most explored part of our space to that unknown side.


Due to this, we quickly get a picture where “tentacles” grow in different directions, which somehow cover our space. Perhaps suboptimally, but rather quickly. The square in the corner is our starting position. Then we can get some way to the goal, which may not be entirely optimal and elegant, but it is obtained in a fairly quick way.

And it turns out, the advantages are that we work very quickly in multidimensional spaces. Since we get the paths through fair simulation, we can almost directly transfer them to the control unit. Disadvantages? We have no guarantees that our points will be chosen well enough. Solutions can turn out pretty curves and not always optimal.
Specialized methods. When the car drives in the city, we have no abstract points A and B and an unstructured environment with random obstacles. In our city, everything is more or less clear: there are concrete lanes and the movement of our car almost always lies in the fact that we drive approximately in the center of the lane, sometimes we shift to the left or to the right to go around the obstacle, sometimes we rebuild to turn according to the rules of the road wherever needed. At the intersections from one lane to another we are rebuilding.


We do not always need these tricky trees to park or make difficult maneuvers. , , - , - -. , . , , , , . . , .

, . , , . , , , , . . , - , , . .
, , . .

, , . , , , . , . . , . , — , , . .

— , . — . . , — . Thank you very much.
Source: https://habr.com/ru/post/340674/
All Articles