Traveling from Moscow to Kazan through St. Petersburg or the process of developing an algorithm for finding all paths
This material is published with the expectation of novice programmers and non-specialists ...
One evening, after reading books about traveling, it seems that it was the famous “Journey from St. Petersburg to Moscow” by Radishchev and “Tarantas” by Vladimir Sollogub - I sat down to watch a lecture on the Dijkstra algorithm. I watched, drew something on a piece of paper and drew a oriented graph. After some thinking, I wondered how I would implement an algorithm for finding all paths from one starting point (a) to some other unique end point (f) on a directed graph. I already began to read about the search algorithms in depth and width , but I thought that it would be more interesting to try to "invent" the algorithm again, often because with this approach you can get an interesting modification of the already known algorithm. At the same time I set myself several conditions: 1) not to use literature; 2) use a non-recursive approach; 3) to store edges in separate arrays, without nesting. Next, I will try to describe the process of finding the algorithm and its implementation, as usual in PHP.
The graph itself turned out like this:
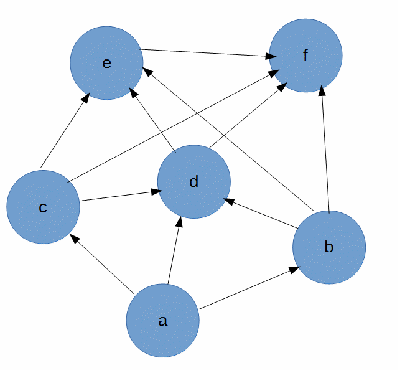
')
In general: the input is an oriented graph with six vertices, the task is to find all the paths from a to f without recursion and with minimal expenditures.
Edges are stored in several arrays, the name of the array is the top:
To get the first path, I decided to go through the zero indices of each array and merge them into one line x (the found path will be stored in this variable at each stage). But how to do it with minimal cost? It seemed to me that the simplest option would be to introduce another array - initializing.
In the array of int all the elements that are in the graph in reverse order.
Then getting the first path is very simple, just cycle through all the arrays,
add a new value to x using concatenation, and at each stage use an element from the previous array as a pointer to the next array.
This style is a bit like bash, but the code looks pretty straightforward:
And so, we got the first path x = abdef .
We can bring it to the screen and deal directly with the algorithm itself, since everything that was higher is only a preparatory part. In theory, it would be possible to get rid of it, but I leave it and publish it so that the train of thought is better understood.
We display the first path and run the first function.
The algorithm itself is actually reduced to two cycles, which are made into separate functions.
The first function takes the previously received first path x . Further in the loop, the traversal x is performed from right to left. We are looking for two elements, one of which will be
work as a pointer to an array, another (right, it’s only worth remembering that the array is upside down) as a pointer to an array element. Using array_search, find the key of the element and check if there is anything in this array after it. If there is, then we replace the element with the one found, but before that we cut off the tail (for this, substr is needed). The replacement can be organized in another way:
A condition with isset needs the interpreter not to throw a warning. It has nothing to do with the algorithm itself. If no elements were found in the arrays, the algorithm will end, but if the miracle did happen, then we move to a new function, the essence of which is extremely simple - add the tail to x , display it and ... “draw eight” or loop - return to the function from which we came, but with the new value of x :
The result of the algorithm for the graph, which is shown in the figure above:
abdef
abdf
abef
abf
acdef
acdf
acef
acf
adef
adf
UPDATE:
As a supplement, I will give a brief description of the algorithm obtained:
The edges of the oriented graph are written out in separate arrays in ascending order.
Those. the vertices of the graph and the edges are ordered. This is a prerequisite.
Before the start of the algorithm, we find the first path, which, taking into account the first condition, will be with the smallest names of the vertices. The way of finding is not particularly important.
Description for verification on paper:
At the entrance, the first found path is x = abdef:
1) Moving from right to left through the array x, select two adjacent elements
(except the last) ab d [e] f, the left (d) is used as a pointer to an array
with vertex, right (e) as a pointer to an element of this array.
We look for an element in d after e, if it exists, remove all elements in x to the right of e. We get in x = abde. Replace the right element (e) with the found element.
2) We add (by the second cycle) the right side of the element (or the index of the right element), which was replaced before the last element (f). In this cycle, it is always necessary to take arrays with a 0 index, since arrays are ordered by condition. In this case, we immediately got on the right side the last element x = abdf, so the second cycle will be idling.
3) After the formation of the right side, we return to traversing the array from right to left.
The absence of elements in the first vertex (array a) is the condition of exit from the algorithm.
The same code without functions and recursion, the first path in x is given:
PS
Array option:
A little about the methodology instead of the conclusion.
As a result, the development of such algorithms has turned out to be a rather simple method that can be useful in working with dynamic arrays.
Its general essence is to carry out preparatory actions before launching the main algorithm, in order to simplify the implementation. This should also make the algorithm more transparent and understandable, which in turn should further contribute to its optimization and simplification.
In this case, the technique is divided into three preparatory steps:
1) Determine the presence of order in the data. Ordering, if necessary.
2) Introduction of an intsializing (vector) array on ordered data.
3) Getting the initial path based on the previous step, the meaning of which also consists in simplifying the basic algorithm. In this case, the initial path must also be built taking into account the order of the data so that it does not allow any path to pass.
If there is no order on the vertices of the graph, then an additional step may be necessary, redefining the names of the vertices, actually building an isomorphic graph and creating an array of matches (for example, between real city names and letters of the alphabet). For other cases of algorithmization, the removal of the original path (vector) beyond the limits of cycles was borrowed by me from my past articles on the generation of combinatorial objects: permutations , partitions / compositions , combinations, allocations .
If we talk about specific working implementations, then of course, you should carefully study the possibilities of a particular language for working with dynamic data. In this situation, the use of "variables" to determine the value of one variable as a name for another is only a way to demonstrate the correctness of the algorithm itself. What are the risks of using this approach in the working environment, the author is unknown.
One evening, after reading books about traveling, it seems that it was the famous “Journey from St. Petersburg to Moscow” by Radishchev and “Tarantas” by Vladimir Sollogub - I sat down to watch a lecture on the Dijkstra algorithm. I watched, drew something on a piece of paper and drew a oriented graph. After some thinking, I wondered how I would implement an algorithm for finding all paths from one starting point (a) to some other unique end point (f) on a directed graph. I already began to read about the search algorithms in depth and width , but I thought that it would be more interesting to try to "invent" the algorithm again, often because with this approach you can get an interesting modification of the already known algorithm. At the same time I set myself several conditions: 1) not to use literature; 2) use a non-recursive approach; 3) to store edges in separate arrays, without nesting. Next, I will try to describe the process of finding the algorithm and its implementation, as usual in PHP.
The graph itself turned out like this:

')
In general: the input is an oriented graph with six vertices, the task is to find all the paths from a to f without recursion and with minimal expenditures.
Edges are stored in several arrays, the name of the array is the top:
$a=array('b','c','d'); $b=array('d','e','f'); $c=array('d','e','f'); $d=array('e','f'); $e=array('f'); To get the first path, I decided to go through the zero indices of each array and merge them into one line x (the found path will be stored in this variable at each stage). But how to do it with minimal cost? It seemed to me that the simplest option would be to introduce another array - initializing.
In the array of int all the elements that are in the graph in reverse order.
$int=array('f','e','d','c','b','a'); Then getting the first path is very simple, just cycle through all the arrays,
add a new value to x using concatenation, and at each stage use an element from the previous array as a pointer to the next array.
This style is a bit like bash, but the code looks pretty straightforward:
$x='a'; $z=$a[0]; while (1) { $x.=$z; $z=${$z}[0]; if ($z == 'f') {$x.=$z; break ;} } And so, we got the first path x = abdef .
We can bring it to the screen and deal directly with the algorithm itself, since everything that was higher is only a preparatory part. In theory, it would be possible to get rid of it, but I leave it and publish it so that the train of thought is better understood.
We display the first path and run the first function.
print $x; print '<br>'; search_el ($x,$a,$b,$c,$d,$e); The algorithm itself is actually reduced to two cycles, which are made into separate functions.
The first function takes the previously received first path x . Further in the loop, the traversal x is performed from right to left. We are looking for two elements, one of which will be
work as a pointer to an array, another (right, it’s only worth remembering that the array is upside down) as a pointer to an array element. Using array_search, find the key of the element and check if there is anything in this array after it. If there is, then we replace the element with the one found, but before that we cut off the tail (for this, substr is needed). The replacement can be organized in another way:
function search_el($x, $a, $b, $c, $d, $e) { $j = strlen($x); while ($j != 0) { $j--; if (isset(${$x[$j - 1]})) $key = array_search($x[$j], ${$x[$j - 1]}); if (${$x[$j - 1]}[$key + 1] != '') { $x = substr($x, 0, $j); $x.= ${$x[$j - 1]}[$key + 1]; new_way_search($x, $a, $b, $c, $d, $e); break; } } } A condition with isset needs the interpreter not to throw a warning. It has nothing to do with the algorithm itself. If no elements were found in the arrays, the algorithm will end, but if the miracle did happen, then we move to a new function, the essence of which is extremely simple - add the tail to x , display it and ... “draw eight” or loop - return to the function from which we came, but with the new value of x :
function new_way_search($x, $a, $b, $c, $d, $e) { $z = $x[strlen($x) - 1]; $z = ${$z}[0]; while (1) { $x.= $z; if ($x[strlen($x) - 1] == 'f') break; if ($z == 'f') { $x.= $z; break; } $z = ${$z}[0]; } echo $x; echo '<br />'; search_el($x, $a, $b, $c, $d, $e); } The result of the algorithm for the graph, which is shown in the figure above:
abdef
abdf
abef
abf
acdef
acdf
acef
acf
adef
adf
UPDATE:
As a supplement, I will give a brief description of the algorithm obtained:
The edges of the oriented graph are written out in separate arrays in ascending order.
Those. the vertices of the graph and the edges are ordered. This is a prerequisite.
Before the start of the algorithm, we find the first path, which, taking into account the first condition, will be with the smallest names of the vertices. The way of finding is not particularly important.
Description for verification on paper:
At the entrance, the first found path is x = abdef:
1) Moving from right to left through the array x, select two adjacent elements
(except the last) ab d [e] f, the left (d) is used as a pointer to an array
with vertex, right (e) as a pointer to an element of this array.
We look for an element in d after e, if it exists, remove all elements in x to the right of e. We get in x = abde. Replace the right element (e) with the found element.
2) We add (by the second cycle) the right side of the element (or the index of the right element), which was replaced before the last element (f). In this cycle, it is always necessary to take arrays with a 0 index, since arrays are ordered by condition. In this case, we immediately got on the right side the last element x = abdf, so the second cycle will be idling.
3) After the formation of the right side, we return to traversing the array from right to left.
The absence of elements in the first vertex (array a) is the condition of exit from the algorithm.
The same code without functions and recursion, the first path in x is given:
Spoiler header
<?php // $a=array('b','c','d'); $b=array('d','e','f'); $c=array('d','e','f'); $d=array('e'); $e=array('f'); // $x='abdef'; print $x; print '<br>'; $j=strlen($x); while($j !=0) { // $key = array_search($x[$j], ${$x[$j-1]}); // , if (${$x[$j-1]}[$key+1] != '') { $x=substr($x, 0, $j); $x.= ${$x[$j-1]}[$key+1]; $z=$x[strlen($x)-1]; $z=${$z}[0]; // c while (1) { // f, if ($x[strlen($x)-1]=='f') {$x.=$z; break ;} $x.=$z; $z=${$z}[0]; } // $j=strlen($x); echo $x; echo '<br>'; } $j--; } ?> PS
Array option:
Spoiler header
<?php error_reporting(0); $a=array('b','c','d'); $b=array('d','e','f'); $c=array('d','e','f'); $d=array('e'); $e=array('f'); $x=array('a','b','d','e','f'); print_r ( $x ); print "\n"; $j=count($x)-1; while($j !=0) { $key = array_search($x[$j], ${$x[$j-1]}); if (${$x[$j-1]}[$key+1] != '') { $x=array_slice($x, 0, $j); array_push($x, ${$x[$j-1]}[$key+1]); $z=$x[count($x)-1]; $z=${$z}[0]; while (1) { if ($x[count($x)-1]=='f') { array_push($x, $z); break ;} array_push($x, $z); $z=${$z}[0]; } $j=count($x); print_r ( $x ); echo "\n"; } $j--; } ?> A little about the methodology instead of the conclusion.
As a result, the development of such algorithms has turned out to be a rather simple method that can be useful in working with dynamic arrays.
Its general essence is to carry out preparatory actions before launching the main algorithm, in order to simplify the implementation. This should also make the algorithm more transparent and understandable, which in turn should further contribute to its optimization and simplification.
In this case, the technique is divided into three preparatory steps:
1) Determine the presence of order in the data. Ordering, if necessary.
2) Introduction of an intsializing (vector) array on ordered data.
3) Getting the initial path based on the previous step, the meaning of which also consists in simplifying the basic algorithm. In this case, the initial path must also be built taking into account the order of the data so that it does not allow any path to pass.
If there is no order on the vertices of the graph, then an additional step may be necessary, redefining the names of the vertices, actually building an isomorphic graph and creating an array of matches (for example, between real city names and letters of the alphabet). For other cases of algorithmization, the removal of the original path (vector) beyond the limits of cycles was borrowed by me from my past articles on the generation of combinatorial objects: permutations , partitions / compositions , combinations, allocations .
If we talk about specific working implementations, then of course, you should carefully study the possibilities of a particular language for working with dynamic data. In this situation, the use of "variables" to determine the value of one variable as a name for another is only a way to demonstrate the correctness of the algorithm itself. What are the risks of using this approach in the working environment, the author is unknown.
Source: https://habr.com/ru/post/340646/
All Articles