The task for today: how to determine the rotation angle of the incremental encoder?

Today, in a series of publications about the Arduino of the brain, there is a short article with a small experiment and a couple of recipes. In the comments to one of my past articles, I was accused of counting the encoder pulses with arduynoy - fu so to do:

Optically 1000 / rev encoder and ATMega not having a hardware scheme for working with an encoder (as in the STM32 series, for example) is a dead end.

Further in the comments was a lot of theorizing, which is better to skip. Let's try to test in the gland, as far as a dead end. For a start, what is an incremental encoder? Anyone who remembers the era of pre-optical mice, the answer knows for sure. Inside the encoder there is a disk with cuts, so for clarity, I made a photo of the disk with five hundred cuts:



On the one side of this disk, an LED is placed; on the other, a photodiode


')
Rotating, the disk then transmits light to the photodiode (if the slot is opposite the LED-photodiode pair), it does not pass. At a constant speed of rotation at the output of the photodiode, a beautiful sinusoid is obtained (do not forget that the flow of light may be partially blocked). If this signal is passed through a comparator, then a rectangular signal is obtained. Counting the number of pulses of the signal, we get how much the sensor shaft has turned.

How is the direction of rotation determined? Very simple: the sensor is not one, but two pairs of LED-photodiode. Let's draw our disk, points A and B show the position of photo sensors. When the encoder shaft rotates, we remove two signals from these photosensors:



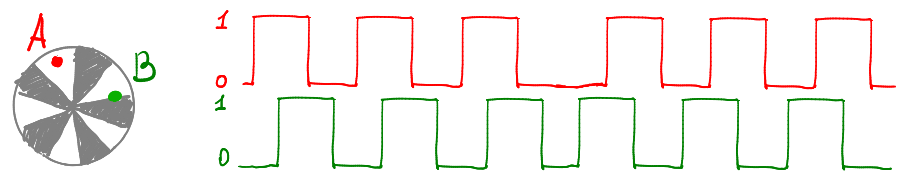
The sensors are placed at such a distance that, when rotated at a constant speed, a square wave is generated that is twisted by a quarter of the period. This means that when the photo sensor A is facing the middle of the slot, the photo sensor B is exactly on the border of the slot. When the sensor rotates (conditionally) clockwise, then at the rising edge on the signal B, the signal A is equal to one. When the sensor rotates in the opposite direction, then with an ascending front on the signal B, a is zero.

This is all great, but what do I copy in my project?

This:

volatile long angle = 0; volatile char ABprev = 0; const int increment[16] = {0,-1,1,0, 1,0,0,-1, -1,0,0,1, 0,1,-1,0}; ISR (PCINT0_vect) { // D8 or D9 has changed char AB = PINB & 3; angle += increment[AB+ABprev*4]; ABprev = AB; } void setup() { pinMode(8, INPUT); // A pinMode(9, INPUT); // B PCICR |= (1 << PCIE0); // interrupt will be fired on any change on pins d8 and d9 PCMSK0 |= 3; ABprev = PINB & 3; Serial.begin(115200); } void loop() { Serial.println(angle); delay(100); } 

Let's explain how this code works. I am testing the code on the ATmega328p (Arduino nano), the encoder outputs are set to pins d8 and d9 arduino nano. In terms of ATmega328p, this means that the lower two bits of the PINB port give the current status of the encoder. The ISR function will be called for any change in these two bits. Inside the interrupt, I save the state of the encoder to the variable AB:

  char AB = PINB & 3; // ,  digitalRead() , //      

For what? Let's look at the previous graph, in it the points of the interrupt call are marked by dashed lines (any front on any signal). For each interrupt call, the number below is the state of the variable AB:



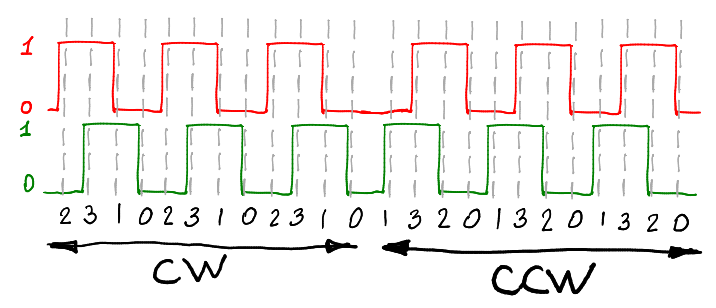
It can be seen that when rotating clockwise, the variable AB changes with a period of four values: 2310 2310 2310. When rotating counter-clockwise, the variable AB changes 0132 0132 0132.

If both photo sensors were blocked (variable AB = 0), and when the interrupt call AB becomes 2, then the sensor rotates clockwise, we add one to the counter. If AB goes from 0 to 1, then the sensor rotates counterclockwise, we subtract one from the counter. The same with other changes to the variable AB, let's create a table:



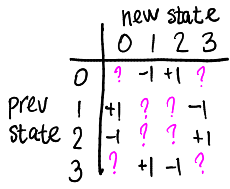
Please note that the table is not fully completed. What to insert in place of question marks? For example, in theory, the main table diagonal should never be used, the interrupt is called when the variable AB is changed, therefore the transition 0-> 0 should not happen. But life is hard, and if the microcontroller is busy, it can skip a few interrupts and still be called. In this case, I suggest not to add or take away anything, since we clearly lack the data; fill the missing cells with zeros, here is our table:

 const int increment[16] = {0,-1,1,0, 1,0,0,-1, -1,0,0,1, 0,1,-1,0}; 

Now, I hope, the code is completely clear.

As a result, four interrupts are called for one period of the signal A, which, when the sensor rotates in one direction, will increase the counter not by 1, but by 4. That is, if 2000PPR is written on the incremental encoder (two thousand slots on the disk), then its real resolution is 1/8000 turnover.

Wait, what about the bounce?

Passing a sine wave through the comparator, we will inevitably get a rattle on the fronts of our rectangular signal. Let's take a magnifying glass and look at one of the fronts:



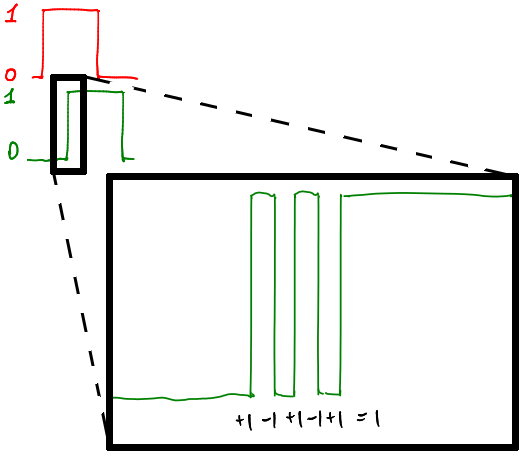
The signal A is constant, therefore, according to our plate, we add one on the rising edge of the signal B, and subtract on the downward one. As a result, if we are able to work out all the fronts of our bounce, then our algorithm will swallow it perfectly. And here it becomes interesting, and whether our arduinka can work out such charms? You can long be theorized, let's experiment.

From theory to practice

We consider pulses in three ways:

• Software on ATmega328p
• ATmega328p, interrogating the hardware counter
• BeagleBone Blue

All three methods consider pulses to be exactly the same, but, of course, hardware methods have a significantly higher signal polling rate. The encoder is used by the Omron E6B2-CWZ6C (2000PPR).

Connection

Software counter

The connection is simple, it is enough to bring two wires from the encoder to the legs of the d8 and d9 arduins.

HCTL-2032

Connecting hctl-2032 to arduine looks like this:



In order not to occupy all the legs of the Arduin, I put another 74hc165.

BeagleBone Blue

BeagleBone Blue has a built-in quadrature decoder, so 3.3V encoders can simply be connected to the appropriate connector. My encoder has 5V logic, so I added a two-way level converter on bss138 :

Experiment one

I took my stand with a pendulum, which was already described :



The carriage will not ride, just hang three counters on the pendulum encoder. Why precisely pendulum? Because gravity gives a non-escape marker: every time the pendulum calms down in the lower position, the counters should show a multiple of 8000 (I have an encoder 2000ppr).

Here are three counters connected in parallel, from top to bottom: biglbon, software counter, hctl2032. The PWM driver for the carriage engine is not used in this test:



The beginning of the test, the pendulum is fixed, two serial port monitors and a bigleon counter, launched via ssh:



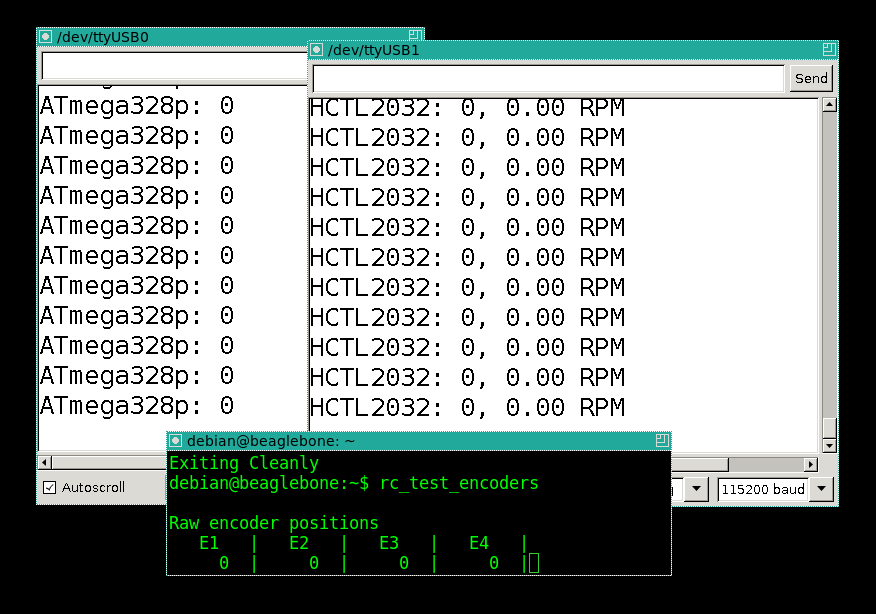
I make one full turn of the pendulum with my hand, and wait until it calms down again in the lower position:



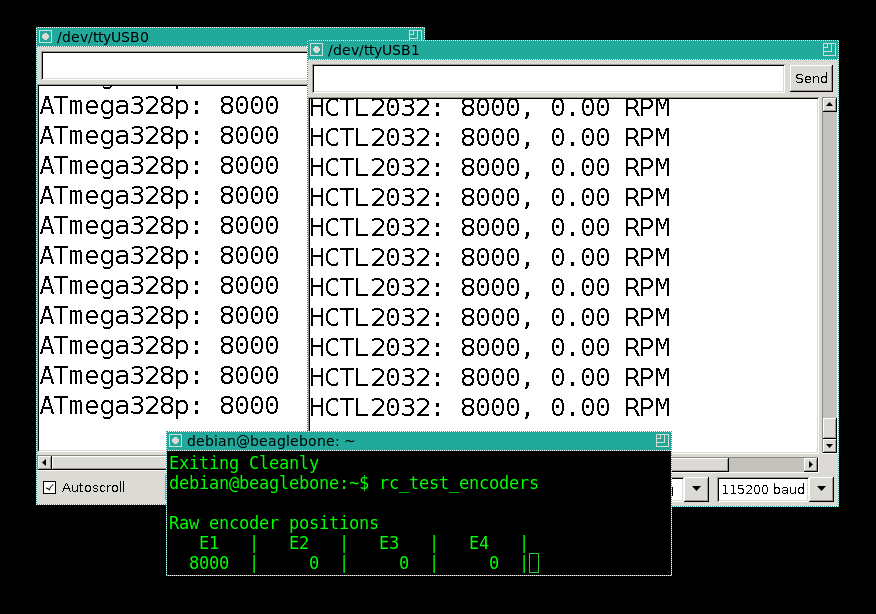
All three counters show exactly 8000, as it should be! Well, from comments we have taken out that because of a bounce the software counter should be mistaken strongly at low speeds of a pendulum. I repeat the procedure ten times: I swing the pendulum so that it makes one revolution, and then I wait until it is completely calm. Then I shake again, waiting for it to calm down. Friction is low, one iteration takes a couple of minutes, in the end, about half an hour of counters.



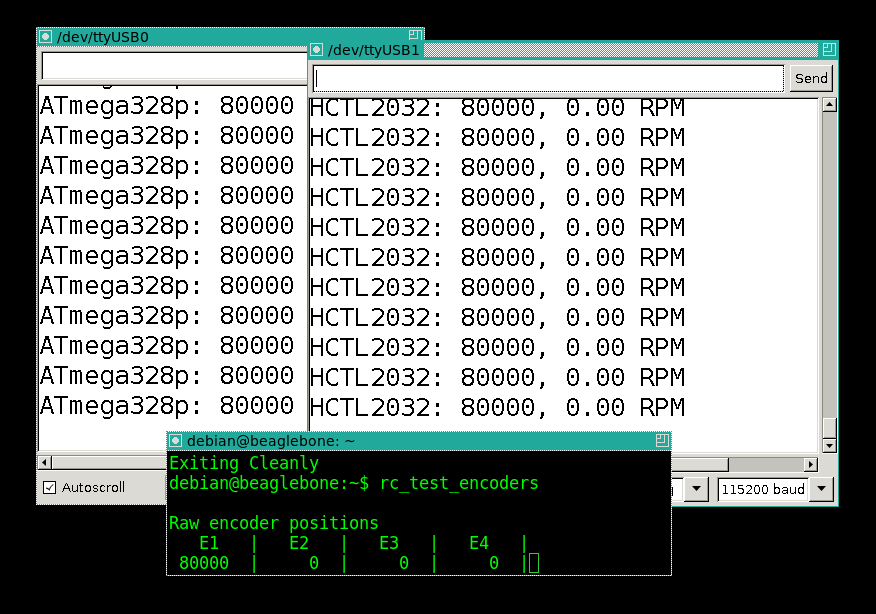
Ha, and yet again, no one was wrong!

Second experiment

So, the bounce in reality turned out to be not as scary as it seemed. I remove the pendulum, and cling to the encoder axis a screwdriver:



Then slowly increase the speed, occasionally stopping, and checking how all three counters agree with what is happening. That is why I have an estimate of the speed of rotation of the encoder shaft in one of the windows.

100 revolutions per minute - order. 500 rpm - order, complete agreement. 900 rpm: AHA! I stop the screwdriver:



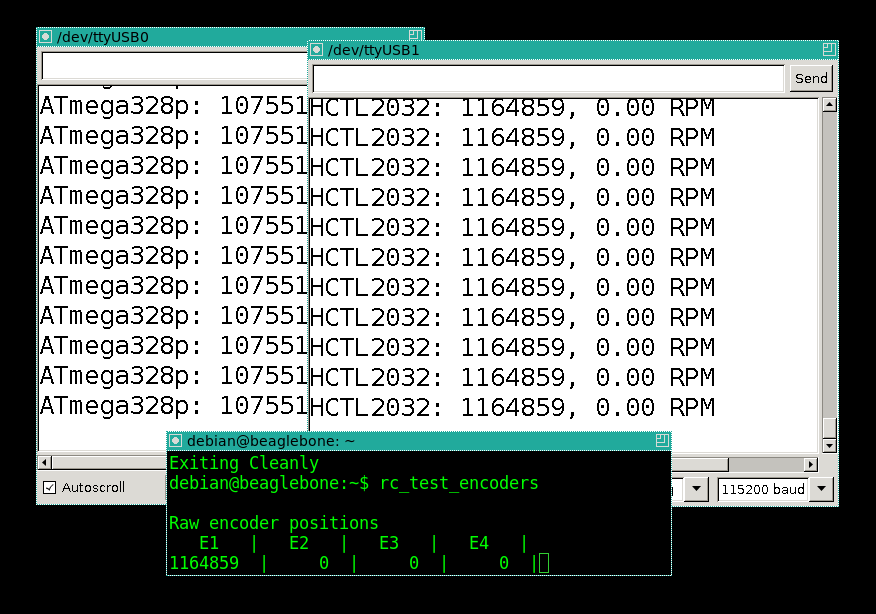
Hardware counters still agree with each other, but the software is well behind. Let's take it as far as consistent with theory. The manual on the ATmega328p says that processing (empty) interrupts is at least 10 microcontroller cycles. Working with the stack, a little code inside the interrupt - this is a total of 40 cycles per interrupt. 8,000 thousand interrupts at 900 revolutions per minute (15 revolutions per second) at 40 cycles = 4,800,000 cycles per second. In general, our estimate is very close to the clock frequency of the Arduin, that is, 1000 revolutions per minute - this is the ceiling for the high resolution encoder counter for interrupts, and for Arduin, which does nothing else.

At 2000 rpm, both hardware counters worked without discrepancies, but I cannot issue a screwdriver anymore.

Summarize:

1. It is quite possible to count on interruptions, 15 revolutions per second is still a very decent speed. But if you need to process more than one counter, everything becomes sharply worse. The choice of the encoder plays a strong role, since in good encoders the chatter suppression is inside, therefore a good encoder and a cheap 8-bit microcontroller are quite a solution.

2. Hardware counters are more reliable, but more expensive.

3. hctl2032 is significantly cheaper than BeagleBone Blue, but it is also more difficult to connect to the controller, and the biglbon and the controller itself are able to process four encoders at once. Yes, and the amplifier for the engine there is already on board, so the stand with the pendulum can be collected at all with little blood. On the other hand, even being rather exotic, the hctl-2032 costs five dollars apiece, and can save the situation when there is already a circuit with some peak or bar and you don’t want to change it much.

4. They say stm32 is cheap and has a hardware counter. But the price of entry (in the sense of time) bites into the question painfully.

In general, as usual, there is no perfect solution, everything depends on the task and on the available resources.