Mathematical Foundations of Bitcoin Blockchain
Today, bitcoin continues to gain popularity, and the industry to develop all new applications for working with cryptocurrency. One of the reasons for this popularity is the rigorous mathematical base on which bitcoin is built.
Due to this, the system functions in conditions of complete lack of trust between the network participants, excluding the impact of the human factor.
Therefore, in today's article we would like to talk about the mathematical foundations of Bitcoin blockchain - elliptic curves, ECDSA and keys.
')
 / Image of Hernán Piñera CC BY
/ Image of Hernán Piñera CC BY
The fundamental part of Bitcoin are cryptographic algorithms. In particular, the ECDSA algorithm is an Elliptic Curve Digital Signature Algorithm, which uses elliptic curves and finite fields to sign data so that a third party can confirm the authenticity of the signature by eliminating the possibility of falsification. ECDSA uses different procedures for signing and verification, consisting of several arithmetic operations.
The elliptic curve over the field K is a cubic curve over the algebraic closure of the field K, defined by a third-degree equation with coefficients from the field K and a “point at infinity”. One form of elliptic curves are Weierstrass curves.
y² = x³ + ax + b
For coefficients a = 0 and b = 7 (used in Bitcoin), the graph of the function takes the following form:
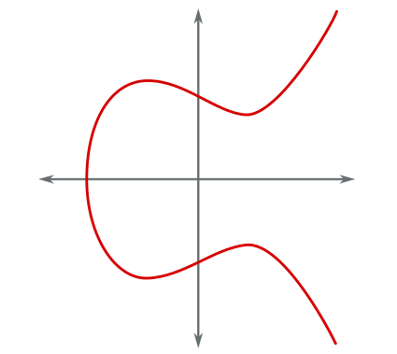
Elliptical curve
Elliptic curves have several interesting properties, for example, a non-vertical line intersecting two non-tangent points on a curve will cross a third point on a curve. The sum of two points on the P + Q curve is called the R point, which is a reflection of the -R point (constructed by continuing the straight line (P; Q) to the intersection with the curve) relative to the X axis.

The sum of two points on the curve ( source )
If we draw a straight line through two points that have coordinates of the form P (a, b) and Q (a, -b), then it will be parallel to the ordinate axis. In this case there will be no third intersection point. To solve this problem, a so-called point at infinity (point of infinity) is introduced, denoted as O. Therefore, if there is no intersection, the equation takes the following form P + Q = O.
If we want to add the point to itself (double it), then in this case the tangent to the point Q is simply drawn. The resulting intersection point is reflected symmetrically with respect to the X axis.
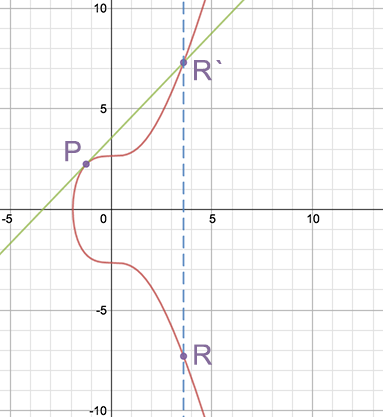
Double point ( source )
These operations allow scalar multiplication of the point R = k * P, adding the point P with itself k times. However, note that faster methods are used to work with large numbers.
In elliptical cryptography (ECC), the same curve is used, only considered over some finite field. The final field in the context of the ECC can be represented as a predefined set of positive numbers, which should be the result of each calculation.
y² = x³ + ax + b (mod p)
For example, 9 mod 7 = 2. Here we have a finite field from 0 to 6, and all operations modulo 7, no matter how many times they are carried out, will give a result that falls in this range.
All the properties mentioned above (addition, multiplication, point at infinity) for such a function remain in force, although the graph of this curve will not resemble an elliptic curve. The Bitcoin elliptic curve, y² = x³ + 7, defined on a finite field modulo 67, looks like this:

Bitcoin elliptic curve defined on a finite field modulo 67 ( source )
This is a set of points where all values of x and y are integers between 0 and 66. The straight lines drawn on this graph will now “wrap” around the field as soon as they reach barrier 67 and continue from the other end of it. while maintaining the same slope, but with a shift. For example, the addition of points (2, 22) and (6, 25) in this particular case looks like this:

Addition of points (2, 22) and (6, 25) ( source )
If you want to see what other elliptic curves look like, you can experiment on this site .
The Bitcoin protocol contains a set of parameters for an elliptic curve and its finite field, so that each user uses a well-defined set of equations. Among the fixed parameters, the equation of the curve (equation), the value of the field modulus (prime modulo), the base point on the curve (base point) and the order of the base point (order) are distinguished. About calculating the order of the base point you can read here . This parameter is chosen specifically and is a very large prime number.
In the case of bitcoin , the following values are used:
The equation of an elliptic curve: y² = x³ + 7
Simple module: 2 256 - 2 32 - 2 9 - 2 8 - 2 7 - 2 6 - 2 4 - 1 = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F
Base point:
04 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8
The bold font is the x coordinate in hexadecimal notation. It is immediately followed by the Y coordinate.
Order: FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141
This set of parameters for an elliptic curve is known as secp256k1 and is part of the SEC (Standards for Efficient Cryptography) family of standards proposed for use in cryptography. In Bitcoin, the secp256k1 curve is used in conjunction with the ECDSA (elliptic curve digital signature algorithm). In ECDSA, a secret key is a random number between one and an order value. The public key is generated based on the secret: the latter is multiplied by the value of the base point. The equation has the following form:
Public key = private key * G
This shows that the maximum number of secret keys (therefore bitcoin addresses) is, of course, equal to the order. However, the order is an incredibly large number, so it is unrealistic to accidentally or intentionally pick up another user's secret key.
The public key is calculated using the same doubling and adding points operations. This is a trivial task that an ordinary personal computer or smartphone solves in milliseconds. But the inverse problem (obtaining a secret key publicly) is a problem of discrete logarithmization , which is considered computationally complex (although there is no strict proof of this fact). The best known algorithms for its solution, like Pollard's ro , have exponential complexity. For secp256k1, to solve the problem, you need about 2,128 operations, which will require a computation time on a regular computer, comparable to the lifetime of the Universe.
When a private / public key pair is obtained, it can be used to sign data. This data can be of any length. Usually, the first step is to hash the data in order to obtain a unique value with the number of bits equal to the bit order of the curve (256). After hashing, the z data signing algorithm is as follows. Here, G is the base point, n is the order, and d is the secret key.
After receiving the data and signing it, a third party, knowing the public key, can verify it. The steps to verify the signature are as follows (Q is the public key):
Indeed,
uG + vQ = u + vdG = (u + vd) G = (zs -1 + rds -1 ) G = (z + rd) s -1 G = kG
The last equality uses the definition of s at the stage of creating a signature.
ECDSA security is related to the complexity of the secret key search task described above. In addition, the security of the original scheme depends on the “randomness” of the choice of k when creating a signature. If the same k value is used more than once, then the secret key can be extracted from the signatures, which is what happened with the PlayStation 3. Therefore, modern implementations of ECDSA, including those used in most bitcoin wallets, generate k determinedly based on the secret key and the message being signed.
PS Bitfury Group Russia in Vk and Fb .
Due to this, the system functions in conditions of complete lack of trust between the network participants, excluding the impact of the human factor.
Therefore, in today's article we would like to talk about the mathematical foundations of Bitcoin blockchain - elliptic curves, ECDSA and keys.
')
 / Image of Hernán Piñera CC BY
/ Image of Hernán Piñera CC BYThe fundamental part of Bitcoin are cryptographic algorithms. In particular, the ECDSA algorithm is an Elliptic Curve Digital Signature Algorithm, which uses elliptic curves and finite fields to sign data so that a third party can confirm the authenticity of the signature by eliminating the possibility of falsification. ECDSA uses different procedures for signing and verification, consisting of several arithmetic operations.
Elliptic curves
The elliptic curve over the field K is a cubic curve over the algebraic closure of the field K, defined by a third-degree equation with coefficients from the field K and a “point at infinity”. One form of elliptic curves are Weierstrass curves.
y² = x³ + ax + b
For coefficients a = 0 and b = 7 (used in Bitcoin), the graph of the function takes the following form:

Elliptical curve
Elliptic curves have several interesting properties, for example, a non-vertical line intersecting two non-tangent points on a curve will cross a third point on a curve. The sum of two points on the P + Q curve is called the R point, which is a reflection of the -R point (constructed by continuing the straight line (P; Q) to the intersection with the curve) relative to the X axis.

The sum of two points on the curve ( source )
If we draw a straight line through two points that have coordinates of the form P (a, b) and Q (a, -b), then it will be parallel to the ordinate axis. In this case there will be no third intersection point. To solve this problem, a so-called point at infinity (point of infinity) is introduced, denoted as O. Therefore, if there is no intersection, the equation takes the following form P + Q = O.
If we want to add the point to itself (double it), then in this case the tangent to the point Q is simply drawn. The resulting intersection point is reflected symmetrically with respect to the X axis.

Double point ( source )
These operations allow scalar multiplication of the point R = k * P, adding the point P with itself k times. However, note that faster methods are used to work with large numbers.
Elliptic curve over a finite field
In elliptical cryptography (ECC), the same curve is used, only considered over some finite field. The final field in the context of the ECC can be represented as a predefined set of positive numbers, which should be the result of each calculation.
y² = x³ + ax + b (mod p)
For example, 9 mod 7 = 2. Here we have a finite field from 0 to 6, and all operations modulo 7, no matter how many times they are carried out, will give a result that falls in this range.
All the properties mentioned above (addition, multiplication, point at infinity) for such a function remain in force, although the graph of this curve will not resemble an elliptic curve. The Bitcoin elliptic curve, y² = x³ + 7, defined on a finite field modulo 67, looks like this:

Bitcoin elliptic curve defined on a finite field modulo 67 ( source )
This is a set of points where all values of x and y are integers between 0 and 66. The straight lines drawn on this graph will now “wrap” around the field as soon as they reach barrier 67 and continue from the other end of it. while maintaining the same slope, but with a shift. For example, the addition of points (2, 22) and (6, 25) in this particular case looks like this:

Addition of points (2, 22) and (6, 25) ( source )
If you want to see what other elliptic curves look like, you can experiment on this site .
Bitcoin ECDSA
The Bitcoin protocol contains a set of parameters for an elliptic curve and its finite field, so that each user uses a well-defined set of equations. Among the fixed parameters, the equation of the curve (equation), the value of the field modulus (prime modulo), the base point on the curve (base point) and the order of the base point (order) are distinguished. About calculating the order of the base point you can read here . This parameter is chosen specifically and is a very large prime number.
In the case of bitcoin , the following values are used:
The equation of an elliptic curve: y² = x³ + 7
Simple module: 2 256 - 2 32 - 2 9 - 2 8 - 2 7 - 2 6 - 2 4 - 1 = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F
Base point:
04 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8
The bold font is the x coordinate in hexadecimal notation. It is immediately followed by the Y coordinate.
Order: FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141
This set of parameters for an elliptic curve is known as secp256k1 and is part of the SEC (Standards for Efficient Cryptography) family of standards proposed for use in cryptography. In Bitcoin, the secp256k1 curve is used in conjunction with the ECDSA (elliptic curve digital signature algorithm). In ECDSA, a secret key is a random number between one and an order value. The public key is generated based on the secret: the latter is multiplied by the value of the base point. The equation has the following form:
Public key = private key * G
This shows that the maximum number of secret keys (therefore bitcoin addresses) is, of course, equal to the order. However, the order is an incredibly large number, so it is unrealistic to accidentally or intentionally pick up another user's secret key.
The public key is calculated using the same doubling and adding points operations. This is a trivial task that an ordinary personal computer or smartphone solves in milliseconds. But the inverse problem (obtaining a secret key publicly) is a problem of discrete logarithmization , which is considered computationally complex (although there is no strict proof of this fact). The best known algorithms for its solution, like Pollard's ro , have exponential complexity. For secp256k1, to solve the problem, you need about 2,128 operations, which will require a computation time on a regular computer, comparable to the lifetime of the Universe.
When a private / public key pair is obtained, it can be used to sign data. This data can be of any length. Usually, the first step is to hash the data in order to obtain a unique value with the number of bits equal to the bit order of the curve (256). After hashing, the z data signing algorithm is as follows. Here, G is the base point, n is the order, and d is the secret key.
- Some integer k is selected from 1 to n-1
- Calculate the point (x, y) = k * G using scalar multiplication
- Is r = x mod n. If r = 0, then return to step 1
- There is s = (z + r * d) / k mod n. If s = 0, then return to step 1
- The resulting pair (r, s) is our signature.
After receiving the data and signing it, a third party, knowing the public key, can verify it. The steps to verify the signature are as follows (Q is the public key):
- Check that both r and s are in the range from 1 to n-1
- Calculated w = s -1 mod n
- Calculated u = z * w mod n
- Calculated v = r * w mod n
- Calculate the point (x, y) = uG + vQ
- If r = x mod n, then the signature is true, otherwise it is invalid.
Indeed,
uG + vQ = u + vdG = (u + vd) G = (zs -1 + rds -1 ) G = (z + rd) s -1 G = kG
The last equality uses the definition of s at the stage of creating a signature.
ECDSA security is related to the complexity of the secret key search task described above. In addition, the security of the original scheme depends on the “randomness” of the choice of k when creating a signature. If the same k value is used more than once, then the secret key can be extracted from the signatures, which is what happened with the PlayStation 3. Therefore, modern implementations of ECDSA, including those used in most bitcoin wallets, generate k determinedly based on the secret key and the message being signed.
PS Bitfury Group Russia in Vk and Fb .
Source: https://habr.com/ru/post/340378/
All Articles