A few years ago an interview was published in which they talk about artificial intelligence and, in particular, about chat bots. The respondent emphasizes that chat bots do not communicate, but imitate communication.

They contain the core of reasonable microdialogues of a completely human level and a communicative algorithm is built for keeping the conversation to this core. That’s all.

In my opinion, there is something in it ...

However, chat bots are talked about a lot on Habré. They can be very different. Popular bots based on neural network prediction, which generate the answer word for word. This is very interesting, but expensive in terms of implementation, especially for the Russian language due to the large number of word forms. I have chosen a different approach to implement the Boltoon chat bot.

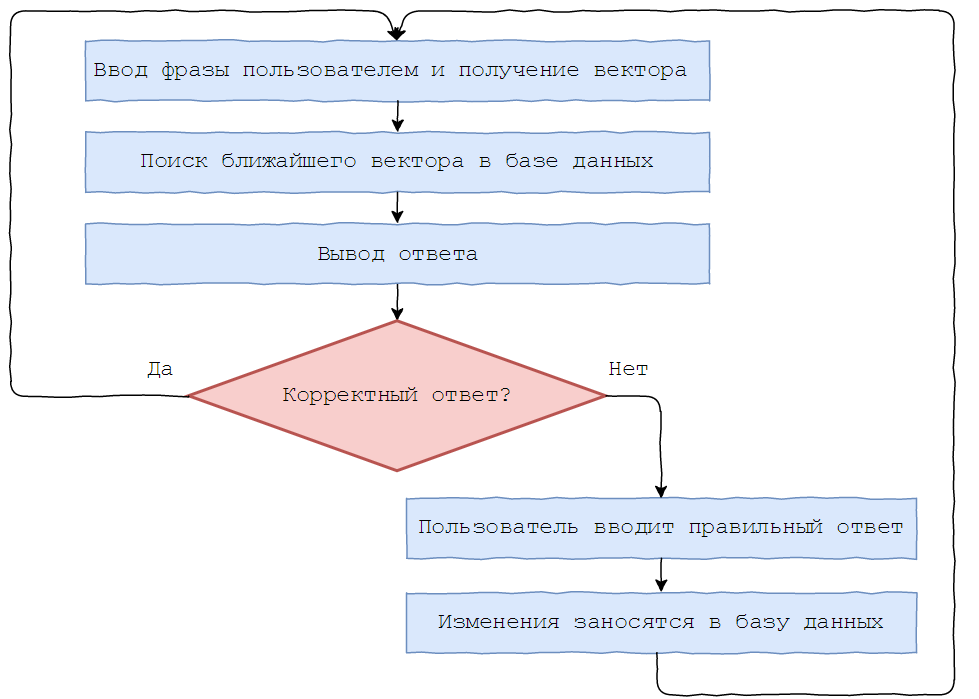
Boltoon works on the principle of selecting the most semantically close response from the proposed database with subsequent processing. This approach has several advantages:
')

• Speed ​​of work;
• Chat bot can be used for different tasks, for this you need to download a new database;
• The bot does not need additional training after updating the database.

How it works?

There is a database with questions and answers to them.



It is necessary that the bot is well aware of the meaning of the entered phrases and found similar in the database. For example, “how are you?”, “How are you?”, “How are you?” Mean the same thing. Since the computer works well with numbers, not letters, the search for matches between the entered phrase and the existing ones should be reduced to a comparison of numbers. It is required to transfer the entire column with questions from the database into numbers, or rather, into vectors of N real numbers. So all documents will receive coordinates in N-dimensional space. It is difficult to present it, but you can reduce the dimension of space to 2 for clarity.



In the same space, we find the coordinate of the phrase entered by the user, compare it with those available by the cosine metric and find the closest one. Boltoon is based on such a simple idea.



Now about everything in order and more formal language. Introduce the concept of "vector representation of the text" (word embeddings) - display $$${word \ Rightarrow \ {R ^ n}}$words from a natural language to a vector of fixed length (usually from 100 to 500 measurements, the higher this value, the more accurate the representation, but it is more difficult to calculate it).

For example, the words "science", "book" can have the following idea:

v ("science") = [0.956, -1.987 ...]
v (“book”) = [0.894, 0.234 ...]

On Habré already wrote about this (you can read in detail here ). The distributed text presentation model is most suitable for this task. Imagine that there is a certain “space of meanings” - the N-dimensional sphere, in which each word, sentence or paragraph will be a point. The question is how to build it?

In 2013, an article appeared “Efficient Estimation of Word Representations in Vector Space” by Thomas Mikolov, in which he speaks about word2vec . This is a set of algorithms for finding a distributed representation of words. Thus, each word is translated to a point in a certain semantic space, and algebraic operations in this space correspond to operations on the meaning of words (therefore, the word semantic is used).

The picture shows this very important property of the space on the example of the vector of "femininity". If we subtract the vector of the word "man" from the vector of the word "king" and add the vector of the word "woman", we get the "queen". You can find more examples in Yandex lectures , also there is an explanation of the word2vec work “for people”, without any special mathematics.



In Python, it looks like this (you need to install the gensim package).

import gensim w2v_fpath = "all.norm-sz100-w10-cb0-it1-min100.w2v" w2v = gensim.models.KeyedVectors.load_word2vec_format(w2v_fpath, binary=True, unicode_errors='ignore') w2v.init_sims(replace=True) for word, score in w2v.most_similar(positive=[u"", u""], negative=[u""]): print(word, score) 

Here, the already built word2vec model is used by the Russian Distributional Thesaurus project.

We get:

  0.856020450592041  0.8100876212120056  0.8040660619735718  0.7984248995780945  0.7981560826301575  0.7949156165122986  0.7862951159477234  0.7808529138565063  0.7741949558258057  0.7644592523574829 

Consider the words nearest to the “king” in more detail. There is a resource for searching for semantically related words, the result is displayed in the form of an ego network. Below are the 20 closest neighbors for the word "king."



The model suggested by Mikolov is very simple - it is assumed that words in similar contexts can mean the same thing. Consider the neural network architecture.



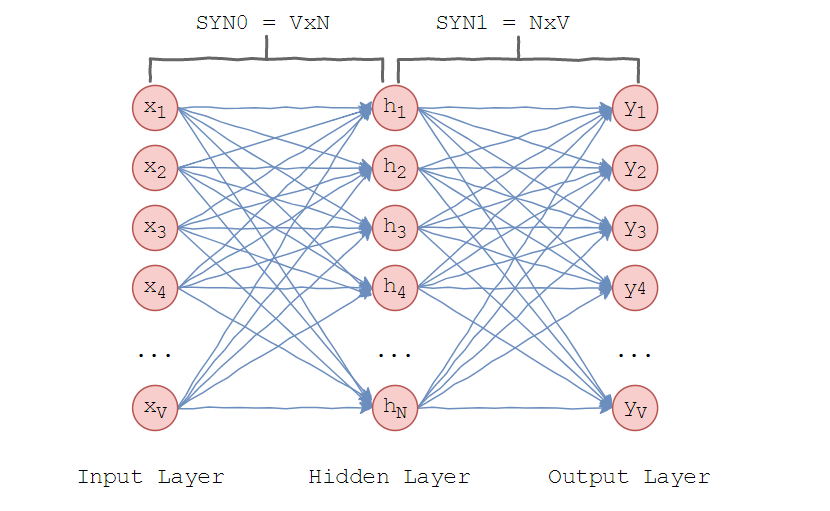
Word2vec uses one hidden layer. In the input layer there are as many neurons as there are words in the dictionary. The size of the hidden layer is the dimension of the space. The size of the output layer is the same as the input. Thus, assuming that the vocabulary for learning consists of V words and N is the dimension of the word vectors, the weights between the input and the hidden layer form a SY × N0 V × N matrix. It represents the following.



Each of the V lines is a vector N-dimensional representation of the word.

$$

$${h = {SYN0 ^ T} x}$$

Similarly, the weights between the hidden and output layers form an N × V matrix SYN1. Then at the input of the output layer will be:

$$

$${val_j = SYN1_j ^ T h}$$

Where $$$SYN1_j$- j-th column of the matrix SYN1.

Scalar product is the cosine of the angle between two points in the n-dimensional space. And this formula shows how close the word vectors are. If the words are opposite, then this value is -1. Then use softmax, the “soft maximum function,” to get the word distribution.

$$

$$y_j = \ frac {exp⁡ ^ {val_j}} {\ sum_ {k \ in V} exp⁡ ^ {val_k}} = softmax$$

Using softmax, word2vec maximizes the cosine measure between vectors of words that occur side by side and minimizes if they do not. This is the output of the neural network.

To better understand how the algorithm works, consider the building for learning, consisting of the following sentences:

"The cat saw the dog,"
"The cat chased the dog",
"White cat climbed a tree."
The corpus dictionary contains eight words: ["white", "climbed", "tree", "cat", "on", "pursued", "dog", "saw"]

After sorting alphabetically, each word can be referenced by its index in the dictionary. In this example, the neural network will have eight input and output neurons. Let there be three neurons in the hidden layer. This means that SYN0 and SYN1 are respectively 8 × 3 and 3 × 8 matrices. Before learning, these matrices are initialized with small random values, as is usually the case when learning. Let SYN0 and SYN1 be initialized as follows:



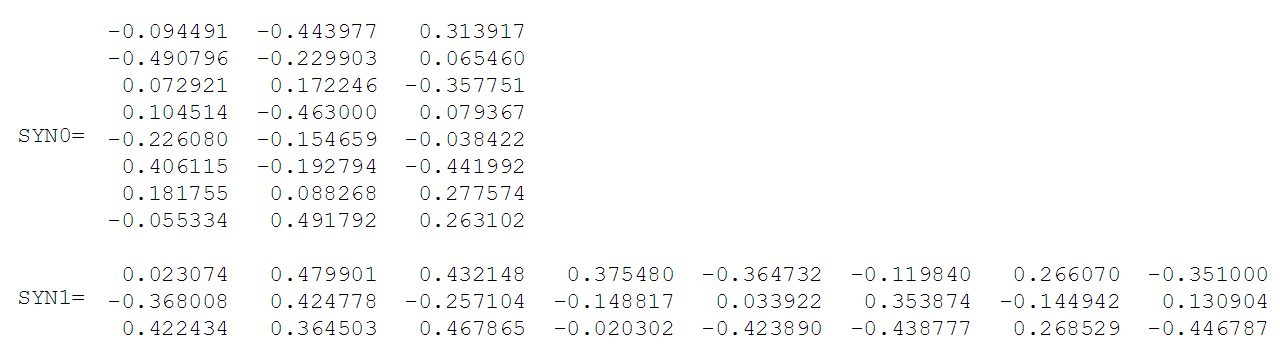
Suppose a neural network must find the relationship between the words "climbed" and "cat." That is, the network should show a high probability of the word "cat" when "climbed" is fed to the input of the network. In the terminology of computational linguistics, the word "cat" is called central, and the word "climbed" is contextual.



In this case, the input vector X will be $$$[0 1 0 0 0 0 0 0] ^ T$(because "climbed" is second in the dictionary). Vector of the word "cat" - $$$[0 0 0 1 0 0 0 0] ^ T$.

When applying to the network a vector representing "climbed", the output on the neurons of the hidden layer can be calculated as follows:

$$

$$H ^ T = X ^ T SYN0 = [- 0.490796, -0.229903, 0.065460]$$

Note that the H vector of the hidden layer is equal to the second row of the SYN0 matrix. Thus, the activation function for the hidden layer is to copy the vector of the input word into the hidden layer.

Similarly for the output layer:

$$

$$\ begin {eqnarray} {H ^ T SYN1 = [0.100934 -0.309331 -0.122361 -0.151399} \ nonumber \\ 0.143463 -0.051262 -0.079686 0.112928] \ end {eqnarray}$$

We need to get the probabilities of words on the output layer, $$$P (word_ {context} word_j)$for $$$k = \ overline {1, V}$which reflect the relation of the central word with the contextual input. To display a vector in probability, use softmax. The output of the jth neuron is calculated by the following expression:

$$$$ display $$ y_j = P (word_ {context} │word_j) = \ frac {exp⁡ ^ {val_j × val_ {context}}} {\ sum_ {k \ in V} exp⁡ ^ {val_j × val_k}} = softmax $$ display $$

Thus, the probabilities for eight words in a corpus are: [0.143073 0.094925 0.114441 0.111166 0.14492 0.122874 0.119431 0.1448800], the "cat" probability is 0.111166 (by index in the dictionary ).

So we compared each word with a vector. But we need to work not with words, but with phrases or with whole sentences, because people communicate that way. For this, there is Doc2vec (originally Paragraph Vector) - an algorithm that gets a distributed representation for parts of texts based on word2vec. Texts can be of any length: from a phrase to paragraphs. And it is very important that at the output we get a vector of fixed length.

Based on this technology Boltoon. First, we build a 300-dimensional semantic space (as mentioned above, choose the dimension from 100 to 500) based on the Russian-language Wikipedia (link to dump ).

A little more python.

 model = Doc2Vec(min_count=1, window=10, size=100, sample=1e-4, workers=8) 

We create an instance of the class for further training with the following parameters:

• min_count: the minimum frequency of occurrence of a word, if the frequency is lower than the specified one - ignore
• window: "window" in which the context is considered
• size: the dimension of the vector (space)
• sample: maximum frequency of occurrence of a word, if the frequency is higher than the specified one - ignore
• workers: number of threads

 model.build_vocab(documents) 

We build a table of dictionaries. Documents - Wikipedia dump.

 model.train(documents, total_examples=model.corpus_count, epochs=20) 

Training. total_examples - the number of documents to enter. Training takes place once. This is a resource-intensive process, building a model of 50 MB of Wikipedia dump (my laptop with 8 GB of RAM no longer pulled). Next, save the trained model, getting these files.



As mentioned above, SYN0 and SYN1 are weights matrices formed during training. These objects are saved to separate files using pickle. Their size is proportional to N × V × W, where N is the dimension of the vector, V is the number of words in the dictionary, W is the weight of one character. This resulted in such a large file size.

We return to the database with questions and answers. Find the coordinates of all the phrases in the newly constructed space. It turns out that with the expansion of the database you will not have to retrain the system, it is enough to take into account the added phrases and find their coordinates in the same space. This is the main advantage of Boltoon - quick adaptation to update data.

Now let's talk about user feedback. Find the coordinate of the question in space and the closest to it phrase that is available in the database. But here the problem arises of finding the nearest point to a given one in N-dimensional space. I propose to use KD-Tree (read more about it here ).

KD-Tree (K-dimensional tree) - a data structure that allows you to split the K-dimensional space into spaces of lower dimension by cutting off the hyperplanes.

 from scipy.spatial import KDTree def build_tree(self, ethalon): return KDTree(list(ethalon.values())) 

But it has a significant drawback: when you add an item, rebuilding the tree is done in O (NlogN) on average, which is long. Therefore, Boltoon uses a “lazy” update — rebuilds the tree every M phrase additions to the database. Search takes place in O (logN).

For the further training of Boltoon, the following functionality was introduced: after receiving the question, an answer is sent with two buttons to assess the quality.



In case of a negative answer, the user is asked to correct it, and the corrected result is entered into the database.



An example of a dialogue with Boltoon using phrases that are not in the database.



Of course, it is difficult to call it “mind,” Boltoon does not possess any mind. He is far from top bots like Siri or recent Alice, but this does not make him useless and uninteresting, after all, this is a student project as part of a summer practice created by one person. In the future, I plan to screw up the processing of responses (coordination with the interlocutor's floor, for example), memorizing the context of the conversation (within the framework of several previous messages) and processing typos. Hopefully it will turn out more reasonable Boltoon 2.0. But this is a conversation for the next article.
PS You can test Boltoon in a telegram via the @boltoon_bot link, just do not forget to evaluate each response received, otherwise your subsequent messages will be ignored. And I see all the logs, who wrote what, so let's observe the limits of decency.
PPS I want to thank my teachers PavelMSTU and ov7a for the advice and constructive criticism of this article.