If you use OOP in practice, you are well-versed in such things as “design patterns” . Do you know that there are many useful patterns that do not fit into this standard list? Unfortunately, many of them are associated with "functional programming", which, according to legend, is complex and abstruse. If you say the word "monoid" ten times, you can call the Devil.

Mark Seeman talks about functional programming quickly and easily. To do this, he began writing a series of articles on the relationship between design patterns and category theory . Any OOshnik, which has 15 minutes of free time, will be able to get into their own hands a fundamentally new set of ideas and insights related not only to the functional area, but also to the correct object-oriented design. The crucial factor is that all the examples are real C #, F #, and Haskell code . This habraposte is a translation of the very beginning of the cycle, the first three articles, merged for convenience of understanding.

In addition, you can talk with Mark live by visiting the DotNext 2017 Moscow conference, which will be held on November 12-13, 2017 in Moscow, at Slavyanskaya Radisson. Mark will read a report on the topic “From dependency injection to dependency rejection” . Tickets are available here .

Introduction. Monoids, semigroups and all-all-all

This text is part of a new series on the relationship between design patterns and category theory .
Functional programming is usually criticized for a special abstruse jargon. Terms like zygohistomorphic prepromorphism do not help to bring the essence to beginners. But before we throw stones, we must first go out of our own glass house. In object-oriented design, names such as Bridge , Visitor , SOLID , connectivity, and others are used. The words sound familiar, but can you explain or implement the Visitor pattern in the code or describe what “connectivity” is?

The word "bridge" does not in itself make object-oriented terminology any better. It may even make it worse. In the end, the word became multivalued: do we mean a real physical object, uniting two different places, or talking about a design pattern? Of course, in practice, we will understand this from the context, but this does not cancel the fact - if someone talks about the bridge pattern, you will understand absolutely nothing if you have not learned it beforehand. The fact that the word sounds familiar does not make it useful.

Many object-oriented programmers have discovered the usefulness of "an operation that returns the same type as it received as an argument." But nevertheless, such a description, such a dictionary is very inconvenient. Wouldn't it be better to describe this operation in one word? Maybe it is a monoid or a semigroup ?

Object Oriented Insights

In Domain-Driven Design, Eric Evans talks about the concept of Closure of Operations . As the name implies, this is an “operation, the return type of which coincides with the types of arguments”. In C #, this may be a method with the signature public Foo Bar(Foo f1, Foo f2) . The method takes two Foo objects as input and returns the Foo object too.

As Evans noted, objects designed in this way begin to look as if they formed arithmetic. If there is an operation that accepts Foo and returns Foo , what could it be? Maybe addition? Multiplication? Any other mathematical operation?

Some enterprise developers just want to "do business and move on," they are not at all worried about mathematics. For them, the idea of ​​making the code more “mathematical” seems very controversial. Nevertheless, even if you “dislike mathematics,” you clearly understand the meaning of addition, multiplication, etc. Arithmetic is a powerful metaphor, as all programmers understand it.

In his famous book , Test-Driven Development: By Example, Kent Beck seemed to be exploiting the same idea. Although I do not think that he wrote about this somewhere directly.

What Evans wrote about is monoids, semigroups and similar concepts from abstract algebra. In fairness, I recently spoke with him, and now he is well versed in all these things. I didn’t know if he understood them in 2003, when DDD was written, but I definitely don’t. My task here is not to poke fingers, but to show that very smart people derived principles that can be used in the PLO, long before these principles got their own names.

How is all this related

Monoids and semigroups belong to a larger group of operations called magmas. We will talk about this later, but now we start with monoids, continue with semigroups, and only then proceed to the magmas. All monoids are semigroups, the reverse is not true. In other words, monoids form a subset of semigroups.

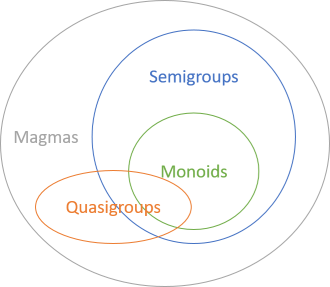
They describe binary operations in the form: an operation that takes two values ​​of Foo as input and returns a value of type Foo at the output. Both categories are described by (intuitive) laws. The difference is that the laws of monoids are stricter than the laws of semigroups. Do not hang out on terminology: the word "law" may sound as if serious complicated mathematics is involved, but these "laws" are simple and intuitive. We will talk about them in the following parts (of which there will be about 15 pieces).

Despite the fact that they are all closely related to mathematics, they are intended to, among other things, give a lot of ideas for a good object-oriented design.

Summary

For an ordinary object-oriented programmer, terms such as a monoid or semigroup a mile away smell math, academy, and ivory towers inhabited by architectural astronauts. But in fact, these are simple and convenient ideas that can be understood by anyone who feels like 15 minutes to do it.

Part 1. Monoids

The bottom line: an introduction to monoids for OOP programmers.
This section is part of a series of articles on monoids, semigroups, and related concepts . Having studied this section, you will understand what a monoid is and how it differs from a semigroup.

Monoids form a subset of semigroups. The rules by which monoids work are stricter than for semigroups. It may even be decided that it is better to first deal with semigroups and move on to monoids based on them. Strictly speaking, in terms of hierarchy, this makes sense. But I think monoids are much more intuitive. Having seen the first example of a monoid, you immediately understand that they describe things from everyday life . It is easy to find an example for a monoid, but to find a good example of a semigroup - you have to try. Therefore, we begin precisely with monoids.

The laws of the monoid

What does addition ( 40 + 2 ) and multiplication ( 6 * 7 ) have in common?
Both of these operations

• associative
• are binary operations
• have a neutral element

This is all that is needed to form a monoid. Associativity and existence of a neutral element are called “monoid laws” or “monoid laws” (in English, monoid laws ). It should be noted that a monoid is a combination of data type and operation. That is, it is not just a type, but rather a function (or method) that works on this type. For example, addition and multiplication are two different monoids working on numbers.

Binary

Let's start with the simplest. An operation is “binary” if it works on two values. Perhaps when the word “binary” is mentioned, you are primarily presented with binary data, such as 101010, but this word came from the Latin language, and means something related to “arity two”. Astronomers also sometimes talk about binary stars (binary stars), but now this word is mainly used in the context of computers: aside from binary data, you most likely have heard of binary trees. Speaking of binary operations, we mean that both incoming values ​​are of the same type, and that the return type also coincides with the incoming type. In other words, in C #, a method like this is the correct binary operation:

 public static Foo Op(Foo x, Foo y) 

Sometimes, if Op is an instance method of the Foo class, it may look like this:

 public Foo Op (Foo foo) 

On the other hand, this is no longer a binary operation:

 public static Baz Op(Foo f, Bar b) 

Although it takes two incoming arguments, they are of different types, and the return type is also different.

Since all the arguments and return values ​​are the same type, the binary operation is what Eric Evans in Domain-Driven Design called Closure of Operations .

Associativity

To form a monoid, a binary operation must necessarily be associative . It simply means that the order of the calculations is not important. For example, to add it means that:

 (2 + 3) + 4 = 2 + (3 + 4) = 2 + 3 + 4 = 9 

Similarly for multiplication:

 (2 * 3) * 4 = 2 * (3 * 4) = 2 * 3 * 4 = 24 

If we talk about the Op method described above, associativity requires that areEqual is true for the following code:

 var areEqual = foo1.Op(foo2).Op(foo3) == foo1.Op(foo2.Op(foo3)); 

On the left side, foo1.Op(foo2) calculated first, and then the result is applied to foo3 . On the right, foo2.Op(foo3) evaluated first, and the result will be the argument for foo1.Op Since the left and right sides are compared using the == operator, associativity requires that areEqual be equal to true .

In order for this whole construct to work in C #, if there is some self-made monoid Foo , it will have to reload Equals and implement the == operator.

Neutral element

The third rule of a monoid is that a neutral element must exist. Usually it is called a unit (not the most appropriate name, but better than the cumbersome "neutral element"). In the future we will call him that.

A unit is a value that "does nothing." For example, for addition it is 0 , because adding zero does nothing with the original value, does not change it:

 0 + 42 = 42 + 0 = 42 

Simple exercise: guess what the unit is for multiplication.

In the above sum entry, it is implied that the unit should be neutral and when it is used on the left and when it is used on the right. For our Foo objects, this can be written as:

 var hasIdentity = Foo.Identity.Op(foo) == foo.Op(Foo.Identity) && foo.Op(Foo.Identity) == foo; 

There are a pair of monoids working on Boolean values: all and any . What do you think, how do they work? What are their units?

You can ponder over all and any (or google them) as an exercise. In the following sections, I will show other, more interesting monoids. In this article, only strings, lists and sequences are considered - the rest of the articles are still being written.

In essence, if there is a data type that “behaves like a number,” you can most likely make a monoid of it. Addition is one of the best candidates, because it is easiest to understand, and you don’t need to get involved with things like units. For example, in the .NET Base Class Library there is a TimeSpan structure that has an Add method. Operator == she also has. On the other hand, TimeSpan does not have the Multiply method, since - what will be the result of multiplying two periods? Square time ?

Summary

A monoid (not to be confused with a monad) is a binary operation that satisfies two laws of a monoid: the operation must be associative and there must exist a neutral element (one). The main examples of a monoid are addition and multiplication, but there are many others.

(By the way, the unit for multiplication is unit (1), all is boolean and , and any is boolean or .)

Part 2. A monoid of strings, lists, and sequences.

Essence: strings, lists and sequences, in fact, are one and the same monoid.
This section is part of a series of articles about monoids .
In short, a monoid is an associative binary operation with a neutral element (known as a unit , or in English terminology, identity ).

Sequences

In C #, lazy sequences of values ​​are modeled using IEnumerable<T> . You can combine a couple of sequences by adding one to the other:

 xs.Concat(ys) 

Here, xs and ys are IEnumerable<T> instances. The Concat extension method combines sequences. It has the following signature: IEnumerable<T> Concat<T>(IEnumerable<T>, IEnumerable<T>) , therefore it is a binary operation. If we find out that it is associative and has a unit, then we prove that it is a monoid.

Sequences are associative, because the sequence of calculation does not change the result. Associativity is a property of a monoid, so one of the ways to demonstrate it is to use property-based testing .

 [Property(QuietOnSuccess = true)] public void ConcatIsAssociative(int[] xs, int[] ys, int[] zs) { Assert.Equal( xs.Concat(ys).Concat(zs), xs.Concat(ys.Concat(zs))); } 

This autotest uses FsCheck (yes, in C # it also works!) To demonstrate Concat associativity. To simplify matters, xs , ys and zs declared as arrays . This is necessary because FsCheck natively knows how to create arrays, but has no built-in support for IEnumerable<T> . Of course, you could create iEnumerable<T> yourself, using the FsCheck API, but this will complicate the example and not add anything new. The associativity property holds for other pure implementations of IEnumerable<T> . If you do not believe it, try it.

Operation Concat has a unit. A unit is an empty sequence, as evidenced by the following test:

 [Property(QuietOnSuccess = true)] public void ConcatHasIdentity(int[] xs) { Assert.Equal( Enumerable.Empty<int>().Concat(xs), xs.Concat(Enumerable.Empty<int>())); Assert.Equal( xs, xs.Concat(Enumerable.Empty<int>())); } 

In other words, if a blank sequence is glued to the beginning or end of any sequence, then the original sequence will not change.

Since Concat is an associative binary operation with a unit, it is a monoid. Proven. ◼

Linked lists and other collections

The above tests using FsCheck showed that Concat is a monoid over arrays. This property holds for all pure IEnumerable<T> implementations.

In Haskell, lazy sequences are modeled as linked lists. They are lazy because all the expressions in Haskell are those by default. The laws of monoids are fulfilled for lists in Haskell:

 λ> ([1,2,3] ++ [4,5,6]) ++ [7,8,9] [1,2,3,4,5,6,7,8,9] λ> [1,2,3] ++ ([4,5,6] ++ [7,8,9]) [1,2,3,4,5,6,7,8,9] λ> [] ++ [1,2,3] [1,2,3] λ> [1,2,3] ++ [] [1,2,3] 

In Haskell, the ++ operator is about the same as Concat in C #, but this operation is called addition or appending ( append ), and not concatenation ( concat ).

In F #, linked lists are initialized aggressively (not lazily), since all expressions in F # are default ones. Lists, however, continue to be monoids, since all the properties of a monoid are still valid:

 > ([1; 2; 3] @ [4; 5; 6]) @ [7; 8; 9];; val it : int list = [1; 2; 3; 4; 5; 6; 7; 8; 9] > [1; 2; 3] @ ([4; 5; 6] @ [7; 8; 9]);; val it : int list = [1; 2; 3; 4; 5; 6; 7; 8; 9] > [] @ [1; 2; 3];; val it : int list = [1; 2; 3] > [1; 2; 3] @ [];; val it : int list = [1; 2; 3] 

In F #, the concatenation operator is @ , not ++ , but its behavior is exactly the same as in Haskell. ◼

Strings

Have you ever wondered why text values ​​are called string in most programming languages? After all, a string in English is a rope , such a long flexible thing made of fibers.

In programming, text is usually presented in memory as a sequential block of characters. Usually the program reads such sequential blocks of memory until it reaches something that is a sign of the end of a line. Thus, the character strings are ordered. They look like sequences or lists.

In fact, in Haskell, the String type is not something tricky, but a synonym for [Char] (meaning: a list of Char values). Therefore, everything that you can do with lists of any other types can also be done with a String :

 λ> "foo" ++ [] "foo" λ> [] ++ "foo" "foo" λ> ("foo" ++ "bar") ++ "baz" "foobarbaz" λ> "foo" ++ ("bar" ++ "baz") "foobarbaz" 

Obviously, ++ for String is a monoid in Haskell.

Similarly, in .NET, System.String implements IEnumerable<char> . By analogy, you can guess that they will be monoids - and this is almost the case. Let's see, they are exactly associative:

 [Property(QuietOnSuccess = true)] public void PlusIsAssociative(string x, string y, string z) { Assert.Equal( (x + y) + z, x + (y + z)); } 

In C #, the + operator is indeed defined for string , and, as can be seen from this test on FsCheck, it is associative. And he almost has a unit. What is the equivalent of an empty list in the string world? Of course, the empty string:

 [Property(QuietOnSuccess = true)] public void PlusHasIdentity(NonNull<string> x) { Assert.Equal("" + x.Get, x.Get + ""); Assert.Equal(x.Get, x.Get + ""); } 

I had to manually explain FsCheck that you do not need to use null . As always, null inserts sticks into the wheels in any arguments about the code.

The problem here is that "" + null and null + "" return the same value - "" , and it is not equal to the incoming value ( null ). In other words, "" not a real unit for the + operator, because this special case exists. (And by the way, null also not a unit, since null + null returns ... "" ! Well, of course, it returns exactly this ...). However, this is a feature of implementation. As an exercise, try to come up with a method (extensions) in C # that would make string regular monoid, despite the presence of null . As soon as you come up with it, it will immediately show that string concatenation is a monoid in .NET in the same way as in Haskell. ◼

Free monoid

Remember how in previous articles we showed that both addition and multiplication of numbers are monoids. There is at least one more monoid over the numbers, and this is a sequence. If there is a generic sequence ( IEnumerable<T> ), it can contain anything, including numbers.

Imagine that there are two numbers, 3 and 4 , and you want to combine them, but it is not yet clear how you will combine them. To postpone a decision, you can put both numbers in a single array (in English, this is called a singleton array — a single element array, and this has nothing to do with the Singleton pattern):

 var three = new[] { 3 }; var four = new[] { 4 }; 

As we have previously proved, sequences are monoids, so you can safely combine them:

 var combination = three.Concat(four); 

The result is a sequence containing both numbers. At the moment, we have not yet lost any information, so as soon as the way to combine these numbers is clear, it will just be necessary to calculate the previously collected data. This is called a free monoid .

For example, we decided to get the sum of numbers:

 var sum = combination.Aggregate(0, (x, y) => x + y); 

(Yes, I am aware that there is a Sum method, but now our goal is to understand the details). This Aggregate takes the seed value as the first argument, and the function for the combination as the second.

And this is how you can get the product:

 var product = combination.Aggregate(1, (x, y) => x * y); 

Note that in both cases the seed value is a unit for the corresponding monoidal operation: 0 for addition, 1 for multiplication. Similarly, the aggregation function uses the binary operation that belongs to the corresponding monoid.

Interestingly, this is called a “free monoid”, similar to the “free monad” . In both cases, it is possible to collect all the data, interpreting them not immediately, but later - and then download all this data into one of the many pre-prepared “calculators”.

Summary

Many types of collections, such as sequences and arrays in .NET or lists in F # and Haskell, are monoids over concatenation. In Haskell, strings are lists, so string concatenation is automatically a monoid. In .NET, the + operator for strings is a monoid, but only if you pretend that null does not exist. However, they are all variations of the same monoid.

It's good that C # uses + for string concatenation, because, as shown in the previous section, addition is the most intuitive and “natural” of all monoids. You know school arithmetic, so you can instantly understand the metaphor of addition. However, a monoid is more than a metaphor. This is an abstraction that describes special binary operations, one of which (as it happens) is addition. This is a generalization of the concept - and this is an abstraction that you already know.

Conclusion

This concludes this article. There is still a lot of information ahead that will be published in the same way as in the original - in the form of consecutive posts on Habré, linked by backward links. Hereinafter: original articles - © Mark Seemann 2016, translations are made by the JUG.ru Group, translator - Oleg Chirukhin.

We remind you that you can talk with the author live by visiting the DotNext 2017 Moscow conference, which will be held on November 12-13, 2017 in Moscow, in “Slavyanskaya Radisson”. Mark will read a report on the topic “From dependency injection to dependency rejection” . Tickets are available here .