Crossing Task
On the Toaster sometimes there are questions about how to learn to think like a programmer. A year ago, for the sake of entertainment, I decided to write a program that solves a well-known puzzle for everyone - a puzzle about a wolf, a goat and cabbage . In English-language sources known as river crossing puzzle.
In this post I will provide you with an example of the thinking process from task to ee to an algorithmic solution.
I must admit that because of the long-term influence of the object-oriented paradigm on my brain, the first thing that occurred to me was for all entities, task participants, to write classes. Problem-oriented programming and all that. But I stopped in time, remembering the old textbooks on pascal, where they operated on the concepts of function and procedure.
In order to translate the task into the plane understood by the machine, we need to get rid of those parts of the task context that does not matter for its solution.
')
Everything that cannot be expressed in numbers does not matter. Cabbage or the ball does not matter, it is important that there are four participants. The river in front of them or the mountain - it does not matter, there are two places where participants of this task can be. On the boat, they are forwarded or on the plane - it does not matter, they can move from one point to another and vice versa, and the peasant (or “man”) is always involved in the movement - a special participant.
In full abstraction, the conditions will look something like this:
To distinguish elements and their combinations, we need to give them identifiers. The machine works best with numbers - we denote them by numbers. We want to combine elements. Combining numbers means doing arithmetic on them.
Then we encode the individual values so that the sum of the numbers uniquely indicates the combination:
0 - no one
1 - P Peasant
2 - G Goat (Goat)
4 - C Cabbage (Cabbage)
8 - W Wolf
The letters here are only for mnemonics and do not carry any load.
The fact that the peasant is designated by the number 1 is important. Because of this, the “shore configuration code” with the farmer will always be odd. So you can understand on which side he is.
We write down the possible combinations on both banks in the form of a table, and we note the permissible options for the distribution of participants along the banks of the X:
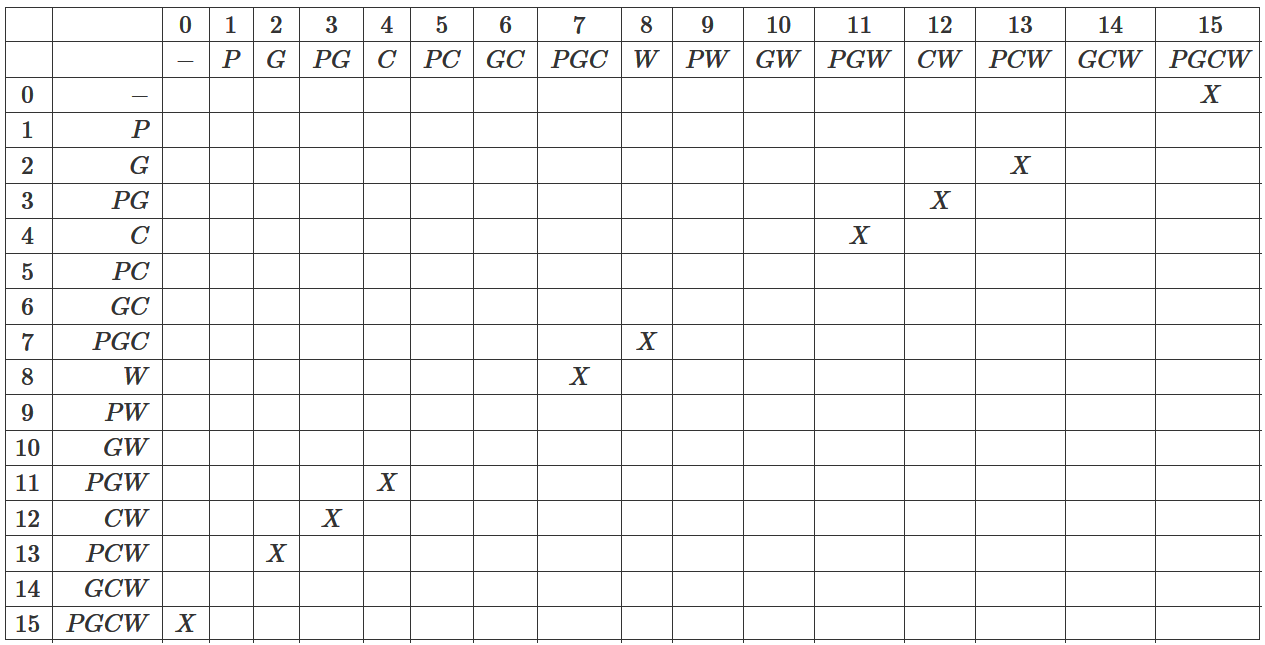
Note that possible combinations of coast configuration always give a total of 15, but not all of them are valid.
From the visual presentation in the form of a table it becomes clear that we need to move from one corner of the table to another, while passing only into admissible states.
Which bank is left and which is right is irrelevant for the task. Ie specifying the configuration code for example 11, we say that on the same bank are a peasant, a goat and a wolf. The fact that the cabbage on the other side does not need to specifically indicate. Since the sum of both banks gives 15, then 4 - cabbage, on the other side.
Let us imagine that our states are stones in water, and we, jumping from stone to stone, must move from one end to another. Reminds tape machine Turing, right?
We can move only in admissible states. Also, from the condition of the problem it is known that a peasant is always involved in the movement and that the boat fits a maximum of two. This means that we can operate with the numbers 1 (peasant), 3 (peasant and goat), 5 (peasant and cabbage), 9 (peasant and wolf).
It turns out that if we start from state 15, when everything on one bank is the only possible next state, it is 12. From state 12 we have no other choice but to return the peasant to the other bank, we do +1. We are moving to state 13. From here we can make either -5 (transport cabbage) or -9 (transport wolf). If we make -9, we’ll get to state 4, but the peasant must be returned after that. We cannot return it alone, otherwise we will be in state 5, but we can return it with a goat +3, and we will be able to 7 (goat cabbage and peasant). From here we can do either -3 (evacuate the goat) or -5 (save the cabbage). Since -3 would be a rollback to the previous action, it remains -5. We move to state 2. From here we can only make +1, and +9 (since +5 would be a rollback of the previous action, a +3 is an invalid state).
Notice, +3 is impossible here not because “the goat is on the other side” (this explanation is understandable to man), but because it is a transition to an unacceptable state (“explanation” understandable to the machine). We do +1. Go to state 3. Do -3. Is done.
But this is not the only possible solution. Note that it is difficult for a person to track all movements. For a machine, there is a set of valid and invalid states, and a set of rules.
Let's make the car find all possible solutions to the problem. Te find all possible chains of states that lead to a solution. We use recursion and python as a language.
For storing chain transitions take an array. The first state is in array 15. Let us pass it to the recursion function. Define the end of recursion condition. This is when the end element of the chain will be 0.
If the state is even (a farmer on the other side), then we perform one of the possible operations with a positive sign (+1, +3, +5 or +9).
For every possible operation, the following conditions must be met:
- it does not lead to an unacceptable state,
- it does not lead for the maximum positive border of the tape
- it does not lead to the state in which we were already.
If such an operation exists, execute it, and add a new state to the chain of states.
Pass the new chain of states to the recursive function.
If the state is odd, then we follow the same considerations, but with a minus sign.
At the output we get
Note that in the solution even and odd numbers alternate. It is the transfer of the peasant from one bank to another. No wonder the above we have designated it as a unit.
We also pay attention to the fact that the initial conditions of the problem, understandable to man, in a software solution turned into numbers and operations on them.
I hope someone this article will be useful.
PS:
If someone has an object-oriented solution, then please share it in the comments so that you can compare the paradigms.
In this post I will provide you with an example of the thinking process from task to ee to an algorithmic solution.
I must admit that because of the long-term influence of the object-oriented paradigm on my brain, the first thing that occurred to me was for all entities, task participants, to write classes. Problem-oriented programming and all that. But I stopped in time, remembering the old textbooks on pascal, where they operated on the concepts of function and procedure.
In order to translate the task into the plane understood by the machine, we need to get rid of those parts of the task context that does not matter for its solution.
')
Everything that cannot be expressed in numbers does not matter. Cabbage or the ball does not matter, it is important that there are four participants. The river in front of them or the mountain - it does not matter, there are two places where participants of this task can be. On the boat, they are forwarded or on the plane - it does not matter, they can move from one point to another and vice versa, and the peasant (or “man”) is always involved in the movement - a special participant.
In full abstraction, the conditions will look something like this:
- There is a set of three elements and one special element.
- There are forbidden combinations of elements (in the absence of a special element)
- In combination with a special element all combinations are allowed.
- It is necessary to transfer all elements from one place to another, so that forbidden combinations of elements are never formed.
- In this case, you can transfer only one element, either to one or to the other side, alternately. Those. you can not make two transfers in one direction. - Thanks to Dr_Dash for focusing on this.
To distinguish elements and their combinations, we need to give them identifiers. The machine works best with numbers - we denote them by numbers. We want to combine elements. Combining numbers means doing arithmetic on them.
Then we encode the individual values so that the sum of the numbers uniquely indicates the combination:
0 - no one
1 - P Peasant
2 - G Goat (Goat)
4 - C Cabbage (Cabbage)
8 - W Wolf
The letters here are only for mnemonics and do not carry any load.
The fact that the peasant is designated by the number 1 is important. Because of this, the “shore configuration code” with the farmer will always be odd. So you can understand on which side he is.
We write down the possible combinations on both banks in the form of a table, and we note the permissible options for the distribution of participants along the banks of the X:

Note that possible combinations of coast configuration always give a total of 15, but not all of them are valid.
From the visual presentation in the form of a table it becomes clear that we need to move from one corner of the table to another, while passing only into admissible states.
Which bank is left and which is right is irrelevant for the task. Ie specifying the configuration code for example 11, we say that on the same bank are a peasant, a goat and a wolf. The fact that the cabbage on the other side does not need to specifically indicate. Since the sum of both banks gives 15, then 4 - cabbage, on the other side.
Let us imagine that our states are stones in water, and we, jumping from stone to stone, must move from one end to another. Reminds tape machine Turing, right?
On the tape, the beginning is indicated by a black triangle on the right, and the end is indicated by an inverted triangle on the left. Possible intermediate states are indicated by black dots. Invalid states are marked with a cross.
We can move only in admissible states. Also, from the condition of the problem it is known that a peasant is always involved in the movement and that the boat fits a maximum of two. This means that we can operate with the numbers 1 (peasant), 3 (peasant and goat), 5 (peasant and cabbage), 9 (peasant and wolf).
It turns out that if we start from state 15, when everything on one bank is the only possible next state, it is 12. From state 12 we have no other choice but to return the peasant to the other bank, we do +1. We are moving to state 13. From here we can make either -5 (transport cabbage) or -9 (transport wolf). If we make -9, we’ll get to state 4, but the peasant must be returned after that. We cannot return it alone, otherwise we will be in state 5, but we can return it with a goat +3, and we will be able to 7 (goat cabbage and peasant). From here we can do either -3 (evacuate the goat) or -5 (save the cabbage). Since -3 would be a rollback to the previous action, it remains -5. We move to state 2. From here we can only make +1, and +9 (since +5 would be a rollback of the previous action, a +3 is an invalid state).
Notice, +3 is impossible here not because “the goat is on the other side” (this explanation is understandable to man), but because it is a transition to an unacceptable state (“explanation” understandable to the machine). We do +1. Go to state 3. Do -3. Is done.
But this is not the only possible solution. Note that it is difficult for a person to track all movements. For a machine, there is a set of valid and invalid states, and a set of rules.
Let's make the car find all possible solutions to the problem. Te find all possible chains of states that lead to a solution. We use recursion and python as a language.
For storing chain transitions take an array. The first state is in array 15. Let us pass it to the recursion function. Define the end of recursion condition. This is when the end element of the chain will be 0.
def f(states): s = states[-1] # , . if s==0: # print(str(states)) print("END") else: # ... print(f([15])) If the state is even (a farmer on the other side), then we perform one of the possible operations with a positive sign (+1, +3, +5 or +9).
For every possible operation, the following conditions must be met:
- it does not lead to an unacceptable state,
- it does not lead for the maximum positive border of the tape
- it does not lead to the state in which we were already.
If such an operation exists, execute it, and add a new state to the chain of states.
Pass the new chain of states to the recursive function.
if s%2 == 0: for i in [9,5,3,1]: if (s+i not in [1,5,6,9,10,14]) and (s+i<=15) and (s+i not in states): f(states+[s+i]) If the state is odd, then we follow the same considerations, but with a minus sign.
else: for i in [9,5,3,1]: if (si not in [1,5,6,9,10,14]) and (si>=0) and (si not in states): f(states+[si]) Complete code
def f(states): s = states[-1] if s==0: print(str(states)) print("END") else: if s%2 == 0: for i in [9,5,3,1]: if (s+i not in [1,5,6,9,10,14]) and (s+i<=15) and (s+i not in states): f(states+[s+i]) else: for i in [9,5,3,1]: if (si not in [1,5,6,9,10,14]) and (si>=0) and (si not in states): f(states+[si]) print(f([15])) At the output we get
[15, 12, 13, 4, 7, 2, 3, 0]
END
[15, 12, 13, 8, 11, 2, 3, 0]
END
None
Note that in the solution even and odd numbers alternate. It is the transfer of the peasant from one bank to another. No wonder the above we have designated it as a unit.
We also pay attention to the fact that the initial conditions of the problem, understandable to man, in a software solution turned into numbers and operations on them.
I hope someone this article will be useful.
PS:
If someone has an object-oriented solution, then please share it in the comments so that you can compare the paradigms.
Source: https://habr.com/ru/post/340124/
All Articles