Why DataScientists do not use errors of the first and second kind

Yesterday, I once again had to explain why DataScientists do not use errors of the first and second kind and why they introduced completeness and accuracy. We have nothing to do here directly, just to introduce new criteria.

And if the error of the second kind is expressed simply:

$$

$$O_2 = 1 - \ Pi$$

where Π is fullness;

then the first kind error is very nontrivially expressed through completeness and accuracy (see below).

But this is the lyrics. The most important question:

Why in DataScience use completeness and accuracy and almost never talk about errors of the first and second kind?

Who does not know or forgot - I ask under cat.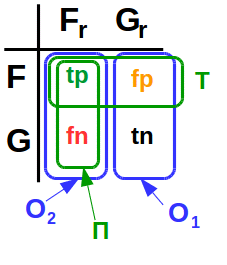

Business challenge

Since Habr is a blog of IT-Schnikov, I will try to use a minimum of mat.abstraktsii and tell immediately on an example. Suppose we solve the Fraud monitoring problem in the RBS of the conditional Roga & Copyta bank , abbreviated R & C.

Suppose that we have developed some kind of automated expert system (ES) that determines for each payment transaction: whether this transaction is fraudulent (fraud, F) or legitimate (genuine, G) .

It is necessary to define "good" criteria for assessing the quality of the system and provide formulas for calculating these criteria.

Since Roga & Copyta is a small, but still a bank, mercantile people work in it and are not interested in anything but money. Therefore, the criteria being developed should show the most transparently : how profitable is it for them to use our ES? Can it be profitable to establish an ES of competitors?

Events and probabilities

Four events can be defined for each transaction:

1. F _r (fraud real) - the probability that the transaction will actually be fraudulent;
2. G _r (genuine real) - the probability that the transaction will actually be legitimate;
3. F is the probability that the ES will “identify” the transaction as fraudulent;
4. G is the probability that the ES will "determine" the transaction as legitimate

Obviously, F _r and G _r are incompatible events ; similarly, F and G are incompatible. For this reason, it is reasonable to consider four probabilities:

$$

$$tn = P (G G_r); ~~ fn = P (GF_r); ~~ fp = P (FG_r); ~~ tp = P (FF_r)$$

Abbreviations read like this:

1. tn - true negative
2. fn - false negative
3. fp - false positive
4. tp - true positive

We can consider conditional probabilities :

$$

$$P (G | G_r); ~~ P (G | F_r); ~~ P (F | G_r); ~~ P (F | F_r)$$

We will also be interested in "reverse" conditional probabilities:

$$$$ display $$ P (G_k | G); ~~ P (G_k | F); ~~ P (F_r | G); ~~ P (F_r | F) $$ display $$

For example, the probability $$$P (F_r | F)$ means the following:

What is the probability that the transaction will indeed be fraudulent if the EC “identified” this event as fraudulent?

It does not follow $$$P (F_r | F)$ confused with $$$P (F | F_r)$ which can be defined by the words:

What is the probability that an ES will call a fraudulent transaction if this transaction is truly fraudulent?

Similarly, you can define words and other conditional probabilities.

Recall the definitions

In statistics, they like to talk about the null hypothesis (H ₀ ) and the alternative (H ₁ ) hypothesis . Usually, the "natural" state is defined under the null hypothesis. In the case of fraud monitoring, the "natural" state is that the transaction is legitimate. This is really reasonable, if only for the reason that the number of fraudulent transactions is much less than the number of legitimate transactions.

Therefore, for the null hypothesis, we take G _r , and for the alternative F _r .

Errors of the first (O ₁ ) and second (O ₂ ) sorts are defined as:

$$

$$O_1 \ stackrel {\ mathrm {def}} {=} P (F | G_r); ~~~~ O_2 \ stackrel {\ mathrm {def}} {=} P (G | F_r)$$

Note : often the error of the first kind is called false positives and the error of the second kind as false negatives. In particular, these are the definitions in Wikipedia . This is true in essence. But $$$fp = P (FG_r) \ neq P (F | G_r) = O_1$ and $$$fn = P (GF_r) \ neq P (G | F_r) = O_2$ . Many newcomers to DataScience make such a mistake and get confused.

Completeness (P) and accuracy (T) by definition:

$$

$$\ Pi \ stackrel {\ mathrm {def}} {=} P (F | F_r); ~~~~ T \ stackrel {\ mathrm {def}} {=} P (F_r | F)$$

Those. Completeness is the likelihood that an ES will “detect” a fraudulent transaction, provided that it is truly fraudulent. And accuracy is the probability that the transaction is really fraudulent, provided that the ES "determined" the transaction as fraudulent.

Completeness and accuracy can be expressed through tp , fp , fn as follows:

$$

$$\ Pi = \ frac {tp} {tp + fn}; ~~ T = \ frac {tp} {tp + fp}$$

It should be noted that these formulas are very often given as a definition of completeness and accuracy. Here the question is in taste. We can say that a square is a rectangle in which all sides are equal and prove that a rhombus with a right angle is a square. And you can do the opposite. For example, when I was in school, my square was defined as a rhombus with a right angle and proved that a rectangle with equal sides is a square.

But still the definition of completeness is $$$\ Pi \ stackrel {\ mathrm {def}} {=} P (F | F_r)$ and accuracy as T $$$\ stackrel {\ mathrm {def}} {=} P (F_r | F)$ seems to me more correct. It is immediately clear what the physical meaning of these quantities is. It is clear why they are needed.

Business sense of completeness and accuracy

Suppose that for Roga & Copyta we created a system with a full 80% and an accuracy of 10% .
Suppose that without an ES, a bank loses 1 billion MNT (₮) a year in fraud. This means that thanks to the ES they will be able to prevent the theft of 800 million. There will be another 200 million - this is damage to the bank (or bank customers), which could not prevent the ES.

And what about 10% accuracy? This value means that only 10 out of 100 ES operation will hit the target, and in other cases we will suspend legitimate transactions. Is it good or bad?

First, when the transaction is stopped, the bank performs any actions. For example calls customers asking for confirmation of operations.

Second, blocking legitimate transactions is not always a good idea either. Imagine that you are sitting with a girl in a restaurant, asking for an invoice, paying with a card ... And then bang ... ES mistakenly calculated that you are a crook ... Probably it will not be very convenient to the young lady ... But we will not over complicate while we lower this problem.

So, suppose one call costs 1000. Also suppose that the average check of a hacker in our country is 100 thousand.

Since we prevent fraud in the amount of 800 million , then on average we will have 8,000 correct fraud draws. But 8000 is, judging by the accuracy, only 10%; hence we’ll call 80,000 times. Multiply this figure by the cost of one call (1000 ₮) and get as much as 80 million!

The total damage per year for a R & C bank is: 200 + 80 = 280 million. But without an ES, the bank would lose one billion. Hence the benefit of R & C is 720 million tugriks.

Business sense of errors of the first and second kind

The error of the second kind is elementarily derived through completeness:

$$

$$O_2 = 1 - \ Pi$$

Formula derivation is elementary (see next paragraph)

Therefore, what to consider - completeness or missed fraud (the error of the second kind) does not represent a particular difference.

And what about the errors of the first kind?

$$

$$O_1 \ stackrel {\ mathrm {def}} {=} P (F | G_r)$$

This is the likelihood that the ES will call a fraudulent transaction a transaction, provided that it is legitimate. The problem is that legitimate transactions are significantly more fraudulent. There are banks in which more than 50 payment transactions per second ... And this is not the limit.

R & C is a small bank, there are only five payment transactions per second. Let's calculate how much it is per day:

$$

$$5 \ cdot 60 \ cdot 60 \ cdot 24 = $ 432,00$$

In the last paragraph, we learned that in the R & C there are 80,000 drawdowns per year, this means that on average, 80,000 / 365 = 219,17 drawdowns per day. Of these, only 10% hit the target (this is the accuracy), that is, 22. So the rest are genuine: 432,000 - 22 = 431978 .

Since the completeness is 80% , of these 22 we will only miss 4.4 .
So the error of the first kind:

$$

$$O_1 = \ frac {4.4} {431978} = 0.000010186$$

Too small! Business does not like such numbers. It is also more difficult than for accuracy to calculate the benefits and damage to the business. And there is another problem:

through an error of the first kind, you can indirectly understand the volume of payment transactions in the bank!

As for accuracy, there is no such problem. Specialists from the R & C security department are aware of fraud volumes. They learn about the permissible load on the contact center from the most important girl + ask the bank management about the desired completeness. Knowing the absolute load, the desired completeness and volume of fraud, you can easily calculate the acceptable accuracy. These two numbers fit into the technical task (or tender).

The developer is given a sample of fraudulent and legitimate transactions. If the sample is representative , this data is sufficient.

"Wrong" accuracy in terms of pure mathematics

If the transaction volume doubles, then accuracy will decrease. If the volume of fraud doubles, the accuracy will also be greater ... With the error of the first kind there is no such problem, therefore from the point of view of "pure mathematics", this value is much more "correct" ...

But in practice, if the amount of fraud increases dramatically, then as a rule this is a fraud of a new type and the EC is simply not trained to catch it ... Accuracy will remain the same (but the fullness will decrease, because fraud will appear, which we do not know how to catch). As for the increase in the number of legitimate transactions, this increase is gradual and there will be no "jerks".

Therefore, in practice, accuracy is a wonderful, understandable for business criterion for assessing the quality of an ES.

The conclusion of the errors of the first kind and the second kind of completeness and accuracy

But maybe there is an elegant formula for finding errors of the first kind through accuracy?
With the error of the second kind, everything is beautiful:

$$

$$O_2 = 1 - \ Pi$$

Unfortunately with O ₁ so gracefully will not work. Here is the ratio through accuracy (T) and completeness (P):

$$

$$O_1 = \ frac {P (F_r)} {P (G_r)} \ cdot \ Pi \ cdot \ left (\ frac {1} {T} - 1 \ right)$$

Conclusion

Accuracy and completeness are "not worse" and "not better" than errors of the first and second kind. It all depends on the task. We do not eat a tablespoon of cake, and tea soup? Although it is possible.

Accuracy and completeness more understandable quality criteria. They are easier to operate. Using them, it is easy to calculate the prevented damage in the fraud monitoring task.

_{If you find a slip or grammatical error - please write in a personal.}