When it is better not to use deep learning
I understand that it is strange to start a blog with a negative, but over the past few days a wave of discussions has risen, which correlates well with some topics that I have been thinking about lately. It all started with Jeff Lick's post on the Simply Stats blog with caution about using in-depth training on a small sample size. He argues that with a small sample size (which is often observed in biology), linear models with a small number of parameters work more efficiently than neural networks, even with a minimum of layers and hidden blocks.
Further, it shows that a very simple linear predictor with the ten most informative features works more efficiently than a simple neural network in the task of classifying zeros and ones in the MNIST data set, using only about 80 samples. This article encouraged Andrew Bima to write a refutation in which a properly trained neural network was able to surpass a simple linear model, even on a very small number of samples.
Such disputes are taking place against the background of the fact that more and more researchers in the field of biomedical informatics are applying in-depth training on various tasks. Is excitement justified, or are linear models enough for us? As always, there is no definite answer. In this article I want to consider cases of machine learning where the use of deep neural networks does not make sense at all. And also to talk about common prejudices that, in my opinion, interfere with the really effective use of deep learning, especially among beginners.
First, let's talk about some prejudices. It seems to me that they are present in the majority of specialists who are not very knowledgeable in the subject of deep learning, but in fact are half-truths. There are two very common and one slightly more technical prejudice - we’ll dwell on them. It is in some way a continuation of the magnificent chapter of “Delusion” in the article by Andrew Beam .
')
In-depth training has become famous for efficient processing of a large amount of input data (remember that the first Google Brain project involved loading a large number of YouTube videos into a neural network), and has since been constantly described as complex algorithms that work on a large amount of data. Unfortunately, this pair of big data and depth learning somehow led people to the opposite thought: the myth that depth learning cannot be used on small samples.
If you have only a few samples, launching a neural network with a high ratio of parameters to a sample at first glance may seem like a direct way to retraining. However, simply taking the sample size and dimension into account for this particular problem, when training with a teacher or without a teacher, is something like modeling data in a vacuum, without context. But you need to consider that in such cases you have relevant data sources or convincing preliminary data that an expert in this field can provide, or the data is structured in a very specific way (for example, in the form of a graph or image). In all of these cases, it is likely that in-depth training will benefit — for example, you can encode useful representations of larger, related data sets and use them in your task. A classic example of such a situation is often found in natural language processing, where you can learn information about the inclusion of individual words in a large dictionary building such as Wikipedia, and then use the information about the inclusion of words on a smaller, narrow body when teaching with a teacher.
In the extreme case, you may have several neural networks that together assimilate the representation and the effective way of its reuse on small sets of samples. This is called one-shot learning from the first time, and it is successfully used in various fields with multidimensional data, including computer vision and the discovery of new drugs.
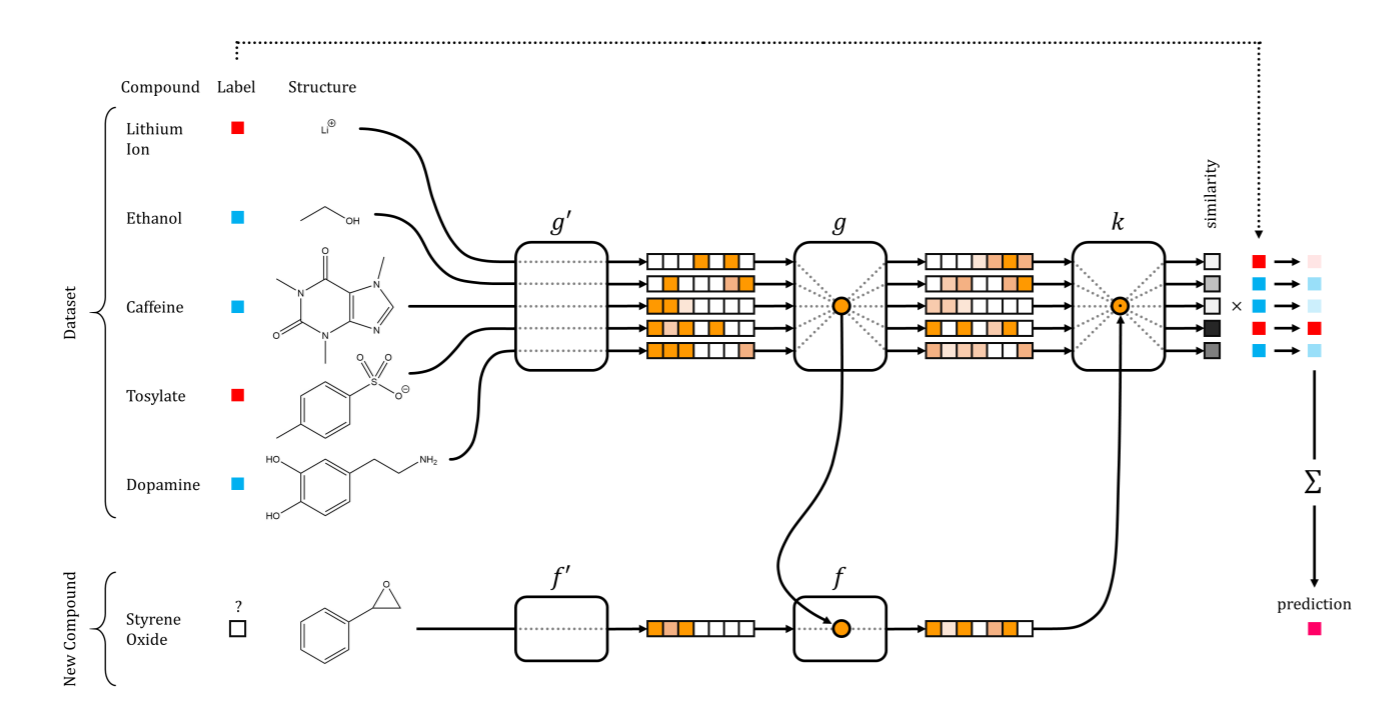
Learning networks from the first time in the discovery of new drugs. Illustration from the article Altae-Tran et al. ACS Cent. Sci. 2017
The second misconception that one often hears is a real hyip. Many experts who begin to practice, expect that the deep-seated nets will give them a fabulous jump in productivity gains just because it happens in other areas. Others are impressed by the tremendous success of in-depth training in modeling and manipulating images, sound and linguistics - in the three types of data that are closest to humans - and they plunge into this area, trying to educate the latest trendy architecture of concurrent neural networks. This hype is manifested in different ways.
In-depth training has become an undeniable force in machine learning and an important tool in the arsenal of any data model developer. Its popularity has led to the creation of important frameworks, such as TensorFlow and PyTorch, which are incredibly useful even beyond the depth of learning. The story of his transformation from an underdog into a superstar inspired researchers to revise other methods previously considered obscure, such as evolutionary strategies and reinforced learning. But this is by no means a panacea. In addition to considerations about the absence of freebies, in principle, I can say that models of in-depth training can have important nuances, require careful handling, and sometimes a very costly search for hyperparameters, tuning and testing (for more details, see later in the article). In addition, there are many cases where in-depth training simply does not make sense from a practical point of view, and simpler models work much better.
Deep learning is more than
There is another aspect of depth learning models that, according to my observations, is misunderstood from the point of view of other areas of machine learning. Most textbooks and introductory materials on depth learning describe these models as composed of hierarchically connected layers of nodes, where the first layer receives an input signal, and the last layer produces an output signal, and you can teach them using some form of stochastic gradient descent. Sometimes it can be briefly mentioned how the stochastic gradient descent works and what is the reverse error propagation. But the lion's part of the explanation is devoted to the rich variety of types of neural networks (convolutional, recurrent, etc.). The optimization methods themselves receive little attention, and this is very bad, because they represent an important (if not the most important) part of the work of any network of in-depth training and because knowledge of these specific methods (read, for example, this post by Ferenc Hujar and his scientific the article that is mentioned there), and knowing how to optimize the parameters of these methods and how to share the data for their effective use is extremely important for obtaining good convergence in a reasonable time.
Why exactly stochastic gradients are so important is still unknown, but experts here and there make different assumptions on this matter. One of my favorites is the interpretation of these methods as part of the Bayesian output calculation. In fact, every time you perform some kind of numerical optimization, you expect a Baisso conclusion with certain assumptions. After all, there is a whole region called probability number , which literally grew out of such an interpretation.
The stochastic gradient descent (SGD) is no different, and recent scientific work suggests that this procedure is actually a Markov chain, which, under certain assumptions, demonstrates a stationary distribution, and it can be considered as a kind of variational approximation to the a posteriori probability. So if you stop your SGD and accept the final parameters, you will in reality get samples from this approximate distribution.
This idea seemed very bright to me. It explains a lot, because the parameters of the optimizer (in this case, the speed of learning) now get much more sense. Such an example: how you can change the learning rate parameter in a stochastic gradient descent, so the Markov chain becomes unstable until it finds a wide local minimum covering samples in a large area; thus, you increase the variance of the procedure. On the other hand, if the learning rate is reduced, the Markov chain slowly approaches a narrower local minimum until it converges in a very narrow area; thus, you increase the bias to a certain area.
Another parameter in SGD, batch size, also controls which type of domain the algorithm converges: in wider areas for small packages or in sharper areas with larger packages.

SGD prefers a wide or narrow local minimum, depending on learning speed or packet size.
Such complexity means that the optimizers of deep neural networks come to the fore: this is the core of the model, just as important as the architecture of the layers. In many other models of machine learning this is not. Linear models (even regularization, such as LASSO) and SVM are convex optimization problems that do not have such subtleties and there is only one solution. That is why specialists who came from other areas and / or use tools like scikit-learn cannot understand why it is impossible to find a very simple API with the
So, when is deep learning not the most optimal way to solve a problem? From my point of view, here are the main scenarios where in-depth training will most likely be a hindrance.
Neural networks are very flexible models with many architectures and types of nodes, optimizers and regularization strategies. Depending on the application, your model may have convolutional layers (how wide? With which pooling?) Or a recurrent structure (with or without gates?). It can be really deep (Hourglass, Siamese or one of many other architectures) or with just a few hidden layers (how many blocks to use?). It may contain linear rectification units or other activation functions. It can turn off part of the neurons during training through the drop-out (in which layers? How many neurons is turned off?) And it is necessary, perhaps, to order the weights (l1, l2 or something more strange?). This is not a complete list, there are many other types of nodes, links, and even loss functions - all this can be tested.
It will take a lot of time to experience such a large number of possible hyper-parameters and architectures, even when training a single instance of a large neural network. Google recently boasted that its AutoML pipeline is capable of automatically selecting the most optimal architecture, which is very impressive, but it requires around-the-clock work of more than 800 GPUs in a few weeks, and this is not available to everyone. The bottom line is that learning deep neural networks is expensive, both in computing and in debugging. Such costs do not make sense to solve everyday forecasting problems, so the ROI of setting up a neural network for such problems may be too small, even when setting up small neural networks. Even if you have a large budget and an important task, there is no reason not to try first the alternative methods as an initial level. You may be pleasantly surprised that linear SVM is all you really need.
Depth neural networks are also notoriously known as “black boxes” with high prediction efficiency, but low interpretability. Although in recent times a lot of tools have been created, like salinity cards and differences in activation . They work well in some areas, but not all applications are applicable. Basically, these tools are useful when you want to verify that a neural network is not deceiving you by remembering a dataset or processing certain dummy attributes. But it is still difficult to interpret the contribution of each feature to the overall solution of the neural network.
In such conditions, nothing can compare with linear models, since there the learned coefficients are directly related to the result. This is especially important when it is necessary to explain such interpretations to a wide audience that will make important decisions based on them. For example, physicians need to integrate all kinds of different data to get a diagnosis. The simpler and clearer the link between the variable and the result, the better the physician can take into account this variable, eliminating the possibility of underestimating or overestimating its value. Moreover, there are cases when interpretability is more important than the accuracy of the model (usually deep learning has no equal in accuracy). Thus, legislators may be interested in what effect some demographic variables have, for example, on mortality. And they may be more interested in direct approximation, rather than prediction accuracy. In both cases, depth learning is inferior to simpler, more transparent networks.
The extreme case of model interpretability is when we try to define a mechanistic model, that is, a model that actually captures the phenomenon behind the data. A good example would be to try to predict how two molecules (for example, drugs, proteins, nucleic acids, etc.) react in a certain cellular environment. Or hypothesize how a certain marketing strategy will affect sales. According to experts in this field, in reality there is nothing that can compete with the good old Bayesian methods. This is the best (though not perfect) way to present and draw conclusions about cause-effect relationships. Vicarious recently published a good scientific paper . It shows why this more principled approach gives better generalizations than in-depth training in tasks with video games.
Perhaps this is a controversial point. I found out that there is one area in which in-depth training is great. This is a search for useful data representations for a specific task. A very nice illustration is the above mentioned inclusions of words. Natural language has a rich and complex structure, it can be approximated using neural networks that take into account the context: each word is represented as a vector encoding the context in which the word is used most often. Using information about the inclusions of words obtained as a result of training on a large corpus of words, the processing of natural language can sometimes show much greater efficiency in a specific task on another corpus of words. However, this model may be completely useless if the case is not structured at all.
Let's say you're trying to classify objects by studying unstructured keyword lists. Since keywords are not used in any particular structure (like sentences), it is unlikely that the inclusion of words here will greatly help. In this case, the data is a word bag model. Such a presentation would probably be quite enough to complete the task. However, it can be argued here that word inclusions are calculated relatively simply if you use pre-trained models, and they can better capture the similarity of keywords. However, I would still prefer to start with a bag of words and see if she can make good predictions. In the end, each dimension of a bag of words is easier to interpret than the corresponding layer of the inclusion of the word.
The field of in-depth training is on the rise, well-funded and stunningly growing. By the time you read a scientific article published at the conference, it is likely that two or three iterations of improved models will be released on the basis of this article, which can already be considered obsolete. This is an important warning to all the arguments that I expressed above: in fact, in the near future, in-depth training may be super-useful for all the scenarios mentioned. Tools for interpreting depth learning models for images and individual sentences are getting better. The latest software, like Edward, combines Bayesian modeling and deep neural network frameworks, allowing you to quantify the uncertainty of the parameters of neural networks and make simple Bayesian inference using probabilistic programming and automated variational inference. In the longer term, we can expect a reduction in the dictionary for modeling: it will capture the salient properties that a neural network can have, and thus reduce the space of those parameters that should be tried. So don't forget to look into your arXiv feed, this article of mine may become outdated in a month or two.

Edward combines probabilistic programming with TensorFlow, allowing for the creation of models that simultaneously use depth learning and Bayesian methods. Illustration: Tran et al. ICLR 2017
Further, it shows that a very simple linear predictor with the ten most informative features works more efficiently than a simple neural network in the task of classifying zeros and ones in the MNIST data set, using only about 80 samples. This article encouraged Andrew Bima to write a refutation in which a properly trained neural network was able to surpass a simple linear model, even on a very small number of samples.
Such disputes are taking place against the background of the fact that more and more researchers in the field of biomedical informatics are applying in-depth training on various tasks. Is excitement justified, or are linear models enough for us? As always, there is no definite answer. In this article I want to consider cases of machine learning where the use of deep neural networks does not make sense at all. And also to talk about common prejudices that, in my opinion, interfere with the really effective use of deep learning, especially among beginners.
Destruction of deep learning prejudices
First, let's talk about some prejudices. It seems to me that they are present in the majority of specialists who are not very knowledgeable in the subject of deep learning, but in fact are half-truths. There are two very common and one slightly more technical prejudice - we’ll dwell on them. It is in some way a continuation of the magnificent chapter of “Delusion” in the article by Andrew Beam .
')
Deep learning can really work on small sample sizes.
In-depth training has become famous for efficient processing of a large amount of input data (remember that the first Google Brain project involved loading a large number of YouTube videos into a neural network), and has since been constantly described as complex algorithms that work on a large amount of data. Unfortunately, this pair of big data and depth learning somehow led people to the opposite thought: the myth that depth learning cannot be used on small samples.
If you have only a few samples, launching a neural network with a high ratio of parameters to a sample at first glance may seem like a direct way to retraining. However, simply taking the sample size and dimension into account for this particular problem, when training with a teacher or without a teacher, is something like modeling data in a vacuum, without context. But you need to consider that in such cases you have relevant data sources or convincing preliminary data that an expert in this field can provide, or the data is structured in a very specific way (for example, in the form of a graph or image). In all of these cases, it is likely that in-depth training will benefit — for example, you can encode useful representations of larger, related data sets and use them in your task. A classic example of such a situation is often found in natural language processing, where you can learn information about the inclusion of individual words in a large dictionary building such as Wikipedia, and then use the information about the inclusion of words on a smaller, narrow body when teaching with a teacher.
In the extreme case, you may have several neural networks that together assimilate the representation and the effective way of its reuse on small sets of samples. This is called one-shot learning from the first time, and it is successfully used in various fields with multidimensional data, including computer vision and the discovery of new drugs.

Learning networks from the first time in the discovery of new drugs. Illustration from the article Altae-Tran et al. ACS Cent. Sci. 2017
Deep learning is not a universal solution to all problems.
The second misconception that one often hears is a real hyip. Many experts who begin to practice, expect that the deep-seated nets will give them a fabulous jump in productivity gains just because it happens in other areas. Others are impressed by the tremendous success of in-depth training in modeling and manipulating images, sound and linguistics - in the three types of data that are closest to humans - and they plunge into this area, trying to educate the latest trendy architecture of concurrent neural networks. This hype is manifested in different ways.
In-depth training has become an undeniable force in machine learning and an important tool in the arsenal of any data model developer. Its popularity has led to the creation of important frameworks, such as TensorFlow and PyTorch, which are incredibly useful even beyond the depth of learning. The story of his transformation from an underdog into a superstar inspired researchers to revise other methods previously considered obscure, such as evolutionary strategies and reinforced learning. But this is by no means a panacea. In addition to considerations about the absence of freebies, in principle, I can say that models of in-depth training can have important nuances, require careful handling, and sometimes a very costly search for hyperparameters, tuning and testing (for more details, see later in the article). In addition, there are many cases where in-depth training simply does not make sense from a practical point of view, and simpler models work much better.
Deep learning is more than .fit()
There is another aspect of depth learning models that, according to my observations, is misunderstood from the point of view of other areas of machine learning. Most textbooks and introductory materials on depth learning describe these models as composed of hierarchically connected layers of nodes, where the first layer receives an input signal, and the last layer produces an output signal, and you can teach them using some form of stochastic gradient descent. Sometimes it can be briefly mentioned how the stochastic gradient descent works and what is the reverse error propagation. But the lion's part of the explanation is devoted to the rich variety of types of neural networks (convolutional, recurrent, etc.). The optimization methods themselves receive little attention, and this is very bad, because they represent an important (if not the most important) part of the work of any network of in-depth training and because knowledge of these specific methods (read, for example, this post by Ferenc Hujar and his scientific the article that is mentioned there), and knowing how to optimize the parameters of these methods and how to share the data for their effective use is extremely important for obtaining good convergence in a reasonable time.
Why exactly stochastic gradients are so important is still unknown, but experts here and there make different assumptions on this matter. One of my favorites is the interpretation of these methods as part of the Bayesian output calculation. In fact, every time you perform some kind of numerical optimization, you expect a Baisso conclusion with certain assumptions. After all, there is a whole region called probability number , which literally grew out of such an interpretation.
The stochastic gradient descent (SGD) is no different, and recent scientific work suggests that this procedure is actually a Markov chain, which, under certain assumptions, demonstrates a stationary distribution, and it can be considered as a kind of variational approximation to the a posteriori probability. So if you stop your SGD and accept the final parameters, you will in reality get samples from this approximate distribution.
This idea seemed very bright to me. It explains a lot, because the parameters of the optimizer (in this case, the speed of learning) now get much more sense. Such an example: how you can change the learning rate parameter in a stochastic gradient descent, so the Markov chain becomes unstable until it finds a wide local minimum covering samples in a large area; thus, you increase the variance of the procedure. On the other hand, if the learning rate is reduced, the Markov chain slowly approaches a narrower local minimum until it converges in a very narrow area; thus, you increase the bias to a certain area.
Another parameter in SGD, batch size, also controls which type of domain the algorithm converges: in wider areas for small packages or in sharper areas with larger packages.

SGD prefers a wide or narrow local minimum, depending on learning speed or packet size.
Such complexity means that the optimizers of deep neural networks come to the fore: this is the core of the model, just as important as the architecture of the layers. In many other models of machine learning this is not. Linear models (even regularization, such as LASSO) and SVM are convex optimization problems that do not have such subtleties and there is only one solution. That is why specialists who came from other areas and / or use tools like scikit-learn cannot understand why it is impossible to find a very simple API with the
.fit() method (although there are some tools like skflow that try to reduce simple neural networks to signature .fit() , but this approach seems to me a bit wrong, because the meaning of deep learning is its flexibility).When not to use depth learning
So, when is deep learning not the most optimal way to solve a problem? From my point of view, here are the main scenarios where in-depth training will most likely be a hindrance.
Low budget or minor problems
Neural networks are very flexible models with many architectures and types of nodes, optimizers and regularization strategies. Depending on the application, your model may have convolutional layers (how wide? With which pooling?) Or a recurrent structure (with or without gates?). It can be really deep (Hourglass, Siamese or one of many other architectures) or with just a few hidden layers (how many blocks to use?). It may contain linear rectification units or other activation functions. It can turn off part of the neurons during training through the drop-out (in which layers? How many neurons is turned off?) And it is necessary, perhaps, to order the weights (l1, l2 or something more strange?). This is not a complete list, there are many other types of nodes, links, and even loss functions - all this can be tested.
It will take a lot of time to experience such a large number of possible hyper-parameters and architectures, even when training a single instance of a large neural network. Google recently boasted that its AutoML pipeline is capable of automatically selecting the most optimal architecture, which is very impressive, but it requires around-the-clock work of more than 800 GPUs in a few weeks, and this is not available to everyone. The bottom line is that learning deep neural networks is expensive, both in computing and in debugging. Such costs do not make sense to solve everyday forecasting problems, so the ROI of setting up a neural network for such problems may be too small, even when setting up small neural networks. Even if you have a large budget and an important task, there is no reason not to try first the alternative methods as an initial level. You may be pleasantly surprised that linear SVM is all you really need.
Interpretation and explanation of the model parameters and characteristics for a wide audience
Depth neural networks are also notoriously known as “black boxes” with high prediction efficiency, but low interpretability. Although in recent times a lot of tools have been created, like salinity cards and differences in activation . They work well in some areas, but not all applications are applicable. Basically, these tools are useful when you want to verify that a neural network is not deceiving you by remembering a dataset or processing certain dummy attributes. But it is still difficult to interpret the contribution of each feature to the overall solution of the neural network.
In such conditions, nothing can compare with linear models, since there the learned coefficients are directly related to the result. This is especially important when it is necessary to explain such interpretations to a wide audience that will make important decisions based on them. For example, physicians need to integrate all kinds of different data to get a diagnosis. The simpler and clearer the link between the variable and the result, the better the physician can take into account this variable, eliminating the possibility of underestimating or overestimating its value. Moreover, there are cases when interpretability is more important than the accuracy of the model (usually deep learning has no equal in accuracy). Thus, legislators may be interested in what effect some demographic variables have, for example, on mortality. And they may be more interested in direct approximation, rather than prediction accuracy. In both cases, depth learning is inferior to simpler, more transparent networks.
Determination of cause-effect relationships
The extreme case of model interpretability is when we try to define a mechanistic model, that is, a model that actually captures the phenomenon behind the data. A good example would be to try to predict how two molecules (for example, drugs, proteins, nucleic acids, etc.) react in a certain cellular environment. Or hypothesize how a certain marketing strategy will affect sales. According to experts in this field, in reality there is nothing that can compete with the good old Bayesian methods. This is the best (though not perfect) way to present and draw conclusions about cause-effect relationships. Vicarious recently published a good scientific paper . It shows why this more principled approach gives better generalizations than in-depth training in tasks with video games.
Training on "unstructured" features
Perhaps this is a controversial point. I found out that there is one area in which in-depth training is great. This is a search for useful data representations for a specific task. A very nice illustration is the above mentioned inclusions of words. Natural language has a rich and complex structure, it can be approximated using neural networks that take into account the context: each word is represented as a vector encoding the context in which the word is used most often. Using information about the inclusions of words obtained as a result of training on a large corpus of words, the processing of natural language can sometimes show much greater efficiency in a specific task on another corpus of words. However, this model may be completely useless if the case is not structured at all.
Let's say you're trying to classify objects by studying unstructured keyword lists. Since keywords are not used in any particular structure (like sentences), it is unlikely that the inclusion of words here will greatly help. In this case, the data is a word bag model. Such a presentation would probably be quite enough to complete the task. However, it can be argued here that word inclusions are calculated relatively simply if you use pre-trained models, and they can better capture the similarity of keywords. However, I would still prefer to start with a bag of words and see if she can make good predictions. In the end, each dimension of a bag of words is easier to interpret than the corresponding layer of the inclusion of the word.
Future is depth
The field of in-depth training is on the rise, well-funded and stunningly growing. By the time you read a scientific article published at the conference, it is likely that two or three iterations of improved models will be released on the basis of this article, which can already be considered obsolete. This is an important warning to all the arguments that I expressed above: in fact, in the near future, in-depth training may be super-useful for all the scenarios mentioned. Tools for interpreting depth learning models for images and individual sentences are getting better. The latest software, like Edward, combines Bayesian modeling and deep neural network frameworks, allowing you to quantify the uncertainty of the parameters of neural networks and make simple Bayesian inference using probabilistic programming and automated variational inference. In the longer term, we can expect a reduction in the dictionary for modeling: it will capture the salient properties that a neural network can have, and thus reduce the space of those parameters that should be tried. So don't forget to look into your arXiv feed, this article of mine may become outdated in a month or two.

Edward combines probabilistic programming with TensorFlow, allowing for the creation of models that simultaneously use depth learning and Bayesian methods. Illustration: Tran et al. ICLR 2017
Source: https://habr.com/ru/post/339840/
All Articles