The graphs are large and small: an intellectual solution to the problem of choosing a representation
(Study for programmers or application for Internet search of a new type)

A program that makes an elephant out of a fly (hereinafter referred to as the MC program) showed that the undirected graph of nouns with a given number of letters even contains thousands of vertices, but at the same time it is rather “skinny” (that is, it has relatively few edges) and to the full graph he is far away (see Example 1). Following Charles Wetherell (Charles Wetherell) , the author of the well-known book "Etudes for Programmers" , he chose the genre of etude to present various ways of representing such graphs. (And to draw conclusions from this for automating the choice of presentation — up to, perhaps, to an Internet search of a new type).
')
Example 1. Characteristics of a noun graph with a length of 8 letters.
“Representing performances” - sounds, to say the least, rough, but such roughness, in my opinion, most corresponds to the genre of etude, which outlines several different variations (in Wetherella's expression). Targeting, but not offering a final complete solution for all possible cases. We will not dwell on minor technical details of the implementation, and in order not to overload the study, I will give only the most significant for the essence code fragments. As in the mentioned MS program (including for reasons of code reuse), I will use the old OO Pascal Delphi-7, hoping that such a simple and widely known language is the easiest to understand and, if desired, can be easily translated into more modern universal languages programming. I will not dwell on the fundamentals of graph theory - they, like the others, used below, concepts and terms can be clarified in Wikipedia - in some cases I will give references. But at the same time I completely refuse responsibility for the correctness of wiki articles: in each article, according to the wiki rules, there should be references to authoritative sources, these sources should be used for final clarification.
It is also worth noting that the “lean” graphs that will be discussed are needed not only for games with words, but also for more serious tasks. For example, in computer (mathematical) organic chemistry, chemical molecules are represented as a graph, in which vertices correspond to atoms, and chemical bonds to edges. Such a representation (sometimes called the formal-logical approach) corresponds to the classical structural theory of organic chemistry, which traditionally uses structural formulas and ball-bearing models . And although every modern chemist knows for sure that atoms are not like balls, and the connections between them are not like rods, these models continue to be widely and successfully used in chemistry. The skeletons of organic molecules are mainly composed of tetravalent carbon, thus the degrees of the vertices of the graphs representing them will not exceed four. True, exceptions are possible, so, in the graph of the ferrocene molecule, the vertex corresponding to the iron atom will be of degree 10. The carbon graph skeleton of cyclopropane will be the only complete graph, the others will be strongly incomplete. This study is unlikely to be useful for constant high-volume work with graphs, but I hope that it can be useful for solving situational tasks such as games. And in any case, this simple example will allow us to illustrate the idea of an intellectual solution to the problem of choosing a representation (including using AI).
As in the MC program, in each of our representations we will look for the shortest path between a given pair of vertices of the graph. Let's start with the definition of the TGraph class:
Protected (protected) abstract methods will be needed to replace descendants. For example:
Note that in the dynamic arrays used, indexing starts from zero, while in many books on graph theory the numbering of vertices and edges starts from one. Since we do not need the graph to be connected, when entering (which will be discussed below), we can allow an isolated zero vertex by default and enter the graph from the first vertex from the book.
Representation of a graph using an adjacency matrix (adjMatrix) is perhaps one of the most common and universal representations. In the general case, this matrix can be represented as a directed graph in which the edge (v, u) corresponds to the element adjMatrix [v, u] = true (initialization writes false to all elements). Such a graph can be defined as follows:
The same class can be used for undirected graphs. In this case, the edge of an undirected graph incident to a pair of vertices (v, u) will correspond to the edge (v, u) and (u, v) of the digraph. So we will do. Therefore, the add edge method (addEdgeA) is defined as:
If there are relatively few edges, then the adjacency matrix will be sparse. Work with such matrices is described in detail in the book by S. Pissanecki, Technology of sparse matrices, M .: Mir, 1988 . Here we will not try to apply the rather sophisticated techniques described there, but simply “half out” this matrix using only its lower triangular submatrix - since we do not consider graphs with loops, then we do not need the main diagonal. Define another class:
for which you can use the following initialization method:
In this case, the add edge method (addEdgeA) will look different than for the digraph:
Similarly, isEdgeA methods are implemented differently:
And now let's think about how to deal with very large graphs - for example, in a million vertices? - Even a triangular adjacency matrix of such dimensions can be too big! We make the following definitions:
Considering that we work with “skinny” graphs, in which there are relatively few edges, we will memorize a pair of vertices incident to the edge in the edge edges vector:
Such an approach corresponds to one of the most economical representations of a graph in the form of an adjacency list. In particular, it is very convenient for manual input of graphs. You can use the following format for edge recording:
where v, u are vertices incident to the edge.
Entries are made into a string and separated from each other by commas. Even in simple cases, it is more convenient to enter a string:
than to dial the 3x3 adjacency matrix.
However, as is often the case, saving on the amount of memory can turn out to be time consuming if the program works directly with the edge edges. Indeed, in the isEdgeA method, it may be necessary to iterate over all edges. You can, of course, sort this vector and search by division in half, but for small degrees of each vertex, you can use the faster method. In the vector nbVertex we write the neighbors of each vertex. The number of neighbors for a vertex corresponds to its degree, so the neighbors of the zero vertex will be written as follows:
Further, the neighbors of the first vertex will be written in the same way. The index for each first neighbor of each vertex will be remembered in the nbStart vector:
This indexing is performed by the method using the auxiliary vector nbCount:
The isEdgeA method for a pair of vertices (v, u) will require a search through no more than deg (v) of nbVertex elements:
Note that such a search can be conducted independently from several positions within the specified limits, therefore, if in our very large graph vertices with large degrees will appear, then the search can be easily parallelized. In some algorithms, it may be necessary to add and remove edges. This is easily done in the above representations, but not in the latter case, which is obviously its disadvantage. However, for our goal - finding the shortest path - adding and deleting edges is not required.
Let us turn to the search for the shortest path. The used BFS algorithm is classic, described in detail in many books, retold in Wikipedia, so we omit its description, and give the implementation:
The described classes for three different graph representations were implemented in a separate module for debugging and testing (as well as for demonstration in this study) of which the program was written - let's call it program T. The screenshot with the window of this program is shown in the figure.
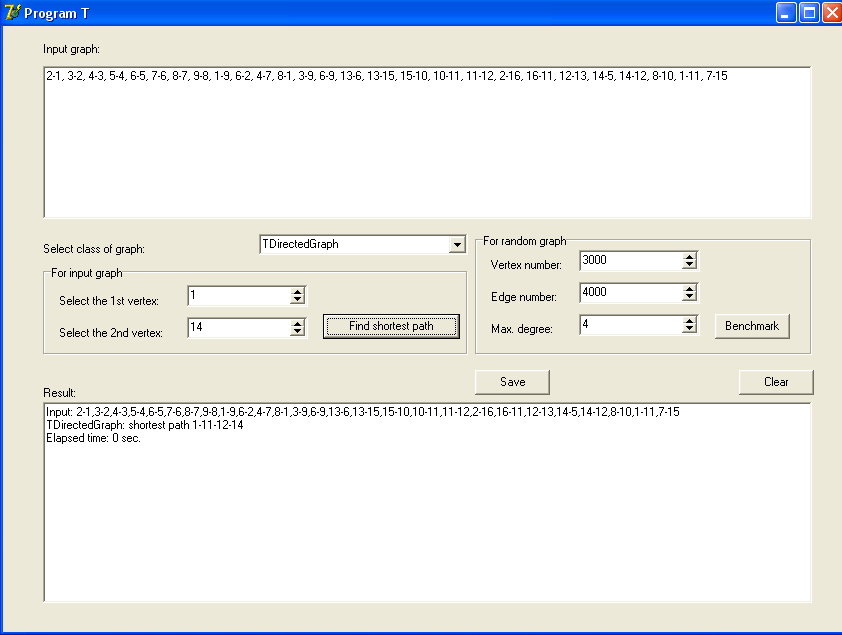
In the Input graph field, you can type a list of the adjacency of the graph in the format described above. In the Result field, the program displays messages and the result of the work. This output can be saved to a text file with the Save button, and the field can be cleared with the Clear button. The drop-down list Select class of graph allows you to select one of the described views. There are not many of them and it would be possible to fill it in by hand during development (in design time), but it is possible that other views will be added in the future, so let the list be filled in during the execution of the program (in run time). To do this, let's do the following simple event handler for creating the main form:
With the graphs created here (dg, ug, bg) the program will continue to work. Parsing and translation of the adjacency list is trivial, so we will not waste readers' attention on their description. Let us go better to the second main test of the program - finding the shortest path between a random pair of vertices (test vertices) in a random graph with user-specified parameters. To generate such a graph, add the following simple method to our parent class. Method parameters - the number of vertices and the maximum degree of the vertex:
To copy the generated graph, you can use the following simple method:
The search for test peaks also did not complicate (for detailed non-etude research on the Internet, you can find many good procedures for generating random graphs):
The maxGen constant took 10, and then how lucky - not all generations are suitable. I will give one of the typical results:
In other distributions, the time difference is even smaller, but the overall trend is
Where t - time.
Thus, it can be assumed that, on the one hand, a change of presentation (from among those used) may not particularly affect speed, but, on the other hand, it is worth testing different ideas for a specific task and for the expected type of graphs. Specially emphasized the word "assume", because the results are too weak for more categorical recommendations. Another task can show qualitatively different results. It is probably impossible to make a choice of any one presentation for all cases. In connection with this, the following thought appears. Usually, programs like the described T program are used in the development of the library and at the final testing stage, but they do not reach the users. At the same time, in many large libraries you can find functions that do the same thing, but with data of different structure and different methods. I think that in such cases it will be very useful if developers apply tools to the libraries to help the user make an informed and informed choice. The next progressive step can be a program that, having received parameters from the user to generate the necessary tests, will make a choice of algorithms and data structures based on the results of these tests and give the user recommendations on the use of library resources. Depending on the task and on the support capabilities, tests can not only be generated, but also downloaded from a local database, from a support site or as a result of a global search on the Internet. In the test sample there may be columns with a feature that is not obvious to the customer. The tests automatically take into account this feature. It will be an intellectual (AI, maybe AI + natural intelligence) solution to the problem of choosing a representation, marked in the title of this etude.
Further more. Now, in order to find the right library, we type in the search engine something like “search for the shortest path in the graph”. Next, we hope for a miracle that will help of hundreds of thousands of links to find the most suitable for our case. If the libraries are equipped with T-programs with a standardized network protocol (you may need new protocols), the user could send a test suite to the search engine, and the T-program servers would run these tests. The search engine would analyze the results and, in response to a request, would provide links to the libraries most appropriate for the given case. At the same time, by sending requests, the search engine can take into account the results of similar previous requests. This will be a search for a new type. Now libraries receive ratings by the number of downloads, and in the case of such a search they will receive ratings on the satisfaction of users' test tasks. Ratings will be highly differentiated: in one group of requests there will be a priority of maximum performance, and in the other, memory savings, and in the third there may be an additional requirement of references only to free libraries, etc. Of course, a comparison of the results obtained on different servers will be very approximate, even with the use of correction factors for the computing capabilities of the server. A final comparison of the pre-selected options will need to be done on the client computer.
Now on the Internet you can find a bunch of various online calculators and file format converters - so it seems that you can count and convert anything online. , offline .
, , , . , ( «» ) . , :
1 , , 8 . , Cardinal (4 ), :
.., .., , 38- « — 2014», . : , 2014, C. 432 . bsf (bit scan forward) CPU 17 . GPU (. ).
— :
: – . . , , , Delphi (maxVertNum) . . , . , , Pascal 8000 OS 360/370 – forall:
:
, – .

A program that makes an elephant out of a fly (hereinafter referred to as the MC program) showed that the undirected graph of nouns with a given number of letters even contains thousands of vertices, but at the same time it is rather “skinny” (that is, it has relatively few edges) and to the full graph he is far away (see Example 1). Following Charles Wetherell (Charles Wetherell) , the author of the well-known book "Etudes for Programmers" , he chose the genre of etude to present various ways of representing such graphs. (And to draw conclusions from this for automating the choice of presentation — up to, perhaps, to an Internet search of a new type).
')
Start for word length 8
6016 words loaded from dictionary file: ..\Dictionary\ORF3.txt
Graph was made: edges number = 871Example 1. Characteristics of a noun graph with a length of 8 letters.
“Representing performances” - sounds, to say the least, rough, but such roughness, in my opinion, most corresponds to the genre of etude, which outlines several different variations (in Wetherella's expression). Targeting, but not offering a final complete solution for all possible cases. We will not dwell on minor technical details of the implementation, and in order not to overload the study, I will give only the most significant for the essence code fragments. As in the mentioned MS program (including for reasons of code reuse), I will use the old OO Pascal Delphi-7, hoping that such a simple and widely known language is the easiest to understand and, if desired, can be easily translated into more modern universal languages programming. I will not dwell on the fundamentals of graph theory - they, like the others, used below, concepts and terms can be clarified in Wikipedia - in some cases I will give references. But at the same time I completely refuse responsibility for the correctness of wiki articles: in each article, according to the wiki rules, there should be references to authoritative sources, these sources should be used for final clarification.
It is also worth noting that the “lean” graphs that will be discussed are needed not only for games with words, but also for more serious tasks. For example, in computer (mathematical) organic chemistry, chemical molecules are represented as a graph, in which vertices correspond to atoms, and chemical bonds to edges. Such a representation (sometimes called the formal-logical approach) corresponds to the classical structural theory of organic chemistry, which traditionally uses structural formulas and ball-bearing models . And although every modern chemist knows for sure that atoms are not like balls, and the connections between them are not like rods, these models continue to be widely and successfully used in chemistry. The skeletons of organic molecules are mainly composed of tetravalent carbon, thus the degrees of the vertices of the graphs representing them will not exceed four. True, exceptions are possible, so, in the graph of the ferrocene molecule, the vertex corresponding to the iron atom will be of degree 10. The carbon graph skeleton of cyclopropane will be the only complete graph, the others will be strongly incomplete. This study is unlikely to be useful for constant high-volume work with graphs, but I hope that it can be useful for solving situational tasks such as games. And in any case, this simple example will allow us to illustrate the idea of an intellectual solution to the problem of choosing a representation (including using AI).
As in the MC program, in each of our representations we will look for the shortest path between a given pair of vertices of the graph. Let's start with the definition of the TGraph class:
TGraph = class(TObject) protected procedure initA (vNum, eNum : integer); virtual; abstract; procedure addEdgeA (v,u : integer); virtual; abstract; function isEdgeA (v,u : integer) : Boolean; virtual; abstract; private vertNum : integer; // edgeNum : integer; // adjMatrix : array of array of Boolean; // degVector : array of integer; // predV : array of integer; // path : array of integer; // pathLen : integer; // ( 1) public testPairV1, testPairV2 : integer; // constructor create; destructor free; function getVertNum : integer; // function getEdgeNum : integer; // function deg (v : integer) : integer; // procedure init (vNum, eNum : integer); // procedure addEdge (v,u : integer); // (v,u) function isVertex (v : integer) : Boolean; // true, 0<=v< vertNum function isEdge (v,u : integer) : Boolean; // true, (v,u) procedure make (eNum,maxDeg : integer); // procedure copy (g : TGraph); // g function BFSsp(v,u : integer) : Boolean; // BFS procedure getShortestPath (v,u : integer); // path function pathToStr {(v : integer)} : string; // path string function getShortestPathStr (v,u :integer) : string; // function findTestPair : string; // end; Protected (protected) abstract methods will be needed to replace descendants. For example:
procedure TGraph.addEdge (v,u : integer); begin addEdgeA (v,u); end; Note that in the dynamic arrays used, indexing starts from zero, while in many books on graph theory the numbering of vertices and edges starts from one. Since we do not need the graph to be connected, when entering (which will be discussed below), we can allow an isolated zero vertex by default and enter the graph from the first vertex from the book.
Representation of a graph using an adjacency matrix (adjMatrix) is perhaps one of the most common and universal representations. In the general case, this matrix can be represented as a directed graph in which the edge (v, u) corresponds to the element adjMatrix [v, u] = true (initialization writes false to all elements). Such a graph can be defined as follows:
TDirectedGraph = class(TGraph) protected procedure initA (vNum,eNum : integer); override; procedure addEdgeA (v,u : integer); override; function isEdgeA (v,u : integer) : Boolean; override; end; The same class can be used for undirected graphs. In this case, the edge of an undirected graph incident to a pair of vertices (v, u) will correspond to the edge (v, u) and (u, v) of the digraph. So we will do. Therefore, the add edge method (addEdgeA) is defined as:
procedure TDirectedGraph.addEdgeA (v,u : integer); var i,j : integer; begin if not adjMatrix [v,u] then begin adjMatrix [v,u] := true; adjMatrix [u,v] := true; inc (edgeNum); // 1 inc(degVector [v]); // 1 v inc(degVector [u]); // 1 u end; end; If there are relatively few edges, then the adjacency matrix will be sparse. Work with such matrices is described in detail in the book by S. Pissanecki, Technology of sparse matrices, M .: Mir, 1988 . Here we will not try to apply the rather sophisticated techniques described there, but simply “half out” this matrix using only its lower triangular submatrix - since we do not consider graphs with loops, then we do not need the main diagonal. Define another class:
TUndirectedGraph = class(TGraph) protected procedure initA (vNum,eNum : integer); override; procedure addEdgeA (v,u : integer); override; function isEdgeA (v,u : integer) : Boolean; override; public procedure clear; end; for which you can use the following initialization method:
procedure TUndirectedGraph.initA (vNum, eNum : integer); var i,j : integer; begin degVector := nil; predV := nil; path := nil; vertNum := vNum; setLength (adjMatrix,vertNum-1); setLength (degVector,vertNum); for i:=0 to vertNum-2 do begin degVector [i] := 0; setLength (adjMatrix [i], i+1); for j := 0 to i do adjMatrix [i,j] := false; end; degVector [vertNum-1] := 0; end; In this case, the add edge method (addEdgeA) will look different than for the digraph:
procedure TUndirectedGraph.addEdgeA (v,u : integer); var i,j : integer; begin if v>u then begin i := v-1; // i := max (v,u)-1; j := u; // j := min (v,u); end else if v<u then begin i := u-1; j := v; end else exit; if not adjMatrix [i,j] then begin adjMatrix [i,j] := true; inc (edgeNum); inc(degVector [i]); inc(degVector [j]); end; end; Similarly, isEdgeA methods are implemented differently:
function TDirectedGraph.isEdgeA (v,u : integer) : Boolean; begin Result := adjMatrix [v,u]; end; function TUndirectedGraph.isEdgeA (v,u : integer) : Boolean; begin if u<v then Result := adjMatrix [v-1,u] else if u>v then Result := adjMatrix [u-1,v] else Result := false; end; And now let's think about how to deal with very large graphs - for example, in a million vertices? - Even a triangular adjacency matrix of such dimensions can be too big! We make the following definitions:
TEdgeRec = record v1,v2 : integer; end; TBigUndirectedGraph = class(TGraph) protected procedure initA (vNum,eNum : integer); override; procedure addEdgeA (v,u : integer); override; function isEdgeA (v,u : integer) : Boolean; override; private edgeIndex : integer; edges : array of TEdgeRec; nbVertex : array of integer; // nbStart : array of integer; // nbCount : array of integer; // public destructor free; procedure calcNb; // end; Considering that we work with “skinny” graphs, in which there are relatively few edges, we will memorize a pair of vertices incident to the edge in the edge edges vector:
procedure TBigUndirectedGraph.addEdgeA (v,u : integer); begin with edges [edgeIndex] do begin v1 := v; v2 := u; end; inc (edgeIndex); inc(degVector [v]); inc(degVector [u]); end; Such an approach corresponds to one of the most economical representations of a graph in the form of an adjacency list. In particular, it is very convenient for manual input of graphs. You can use the following format for edge recording:
vuwhere v, u are vertices incident to the edge.
Entries are made into a string and separated from each other by commas. Even in simple cases, it is more convenient to enter a string:
1-2,2-3,3-1than to dial the 3x3 adjacency matrix.
However, as is often the case, saving on the amount of memory can turn out to be time consuming if the program works directly with the edge edges. Indeed, in the isEdgeA method, it may be necessary to iterate over all edges. You can, of course, sort this vector and search by division in half, but for small degrees of each vertex, you can use the faster method. In the vector nbVertex we write the neighbors of each vertex. The number of neighbors for a vertex corresponds to its degree, so the neighbors of the zero vertex will be written as follows:
NbVertex [0], …, nbVertex[deg(0)-1]Further, the neighbors of the first vertex will be written in the same way. The index for each first neighbor of each vertex will be remembered in the nbStart vector:
nbStart[0]=0, nbStart[1]= deg(0),…This indexing is performed by the method using the auxiliary vector nbCount:
procedure TBigUndirectedGraph.calcNb; var i,n : integer; begin n := 0; for i:=0 to vertNum-1 do begin nbStart [i] := n; nbCount [i] := n; inc (n, degVector [i]); end; for i:=0 to edgeNum-1 do begin nbVertex [nbCount[edges [i].v1]] := edges [i].v2; inc (nbCount[edges [i].v1]); nbVertex [nbCount[edges [i].v2]] := edges [i].v1; inc (nbCount[edges [i].v2]); end; end; The isEdgeA method for a pair of vertices (v, u) will require a search through no more than deg (v) of nbVertex elements:
function TBigUndirectedGraph.isEdgeA (v,u : integer) : Boolean; var i,n,d : integer; begin d := deg (v); if d>0 then begin n := nbStart [v]; for i:=0 to d-1 do begin Result := nbVertex[n+i]=u; if Result then exit; end; end else Result := false; end; Note that such a search can be conducted independently from several positions within the specified limits, therefore, if in our very large graph vertices with large degrees will appear, then the search can be easily parallelized. In some algorithms, it may be necessary to add and remove edges. This is easily done in the above representations, but not in the latter case, which is obviously its disadvantage. However, for our goal - finding the shortest path - adding and deleting edges is not required.
Let us turn to the search for the shortest path. The used BFS algorithm is classic, described in detail in many books, retold in Wikipedia, so we omit its description, and give the implementation:
function TGraph.BFSsp(v,u : integer) : Boolean; // BFS var Qu : array of integer; first, last : integer; i,p : integer; newV : array of Boolean; begin p := v; setLength (predV,vertNum); setLength (newV,vertNum); for i:= 0 to vertNum-1 do newV [i] := true; setLength (Qu,vertNum); first := 0; last := 1; Qu [last] := p; newV [p] := false; while (first<last) and (p<>u) do begin inc (first); p := Qu [first]; for i:=0 to vertNum-1 do if isEdge (p,i) and newV [i] then begin inc (last); Qu [last] := i; newV [i] := false; predV [i] := p; end; end; Result := p = u; Qu := nil; newV := nil; end; // BFSsp procedure TGraph.getShortestPath (v,u : integer); var i,p : integer; begin setLength (path,vertNum); p := u; i := 0; path [0] := p; while p<>v do begin inc (i); p := predV [p]; path [i] := p; end; // inc (i); pathLen := i+1; setLength (path,pathLen); end; // getShortestPath The described classes for three different graph representations were implemented in a separate module for debugging and testing (as well as for demonstration in this study) of which the program was written - let's call it program T. The screenshot with the window of this program is shown in the figure.

In the Input graph field, you can type a list of the adjacency of the graph in the format described above. In the Result field, the program displays messages and the result of the work. This output can be saved to a text file with the Save button, and the field can be cleared with the Clear button. The drop-down list Select class of graph allows you to select one of the described views. There are not many of them and it would be possible to fill it in by hand during development (in design time), but it is possible that other views will be added in the future, so let the list be filled in during the execution of the program (in run time). To do this, let's do the following simple event handler for creating the main form:
procedure TMainForm.FormCreate(Sender: TObject); begin dg := TDirectedGraph.create; ug := TUndirectedGraph.create; bg := TBigUndirectedGraph.create; ComboBoxClass.AddItem(dg.ClassName,dg); ComboBoxClass.AddItem(ug.ClassName,ug); ComboBoxClass.AddItem(bg.ClassName,bg); ComboBoxClass.ItemIndex := 0; end; With the graphs created here (dg, ug, bg) the program will continue to work. Parsing and translation of the adjacency list is trivial, so we will not waste readers' attention on their description. Let us go better to the second main test of the program - finding the shortest path between a random pair of vertices (test vertices) in a random graph with user-specified parameters. To generate such a graph, add the following simple method to our parent class. Method parameters - the number of vertices and the maximum degree of the vertex:
procedure TGraph.make (eNum, maxDeg : integer); var n,i,j : integer; begin randomize; n := 0; repeat i := random (vertNum); // 1- j := random (vertNum); // 2- if (i<>j)and (deg(i)<maxDeg) and (deg(j)<maxDeg) then begin addEdge (i,j); inc (n); end; until n= eNum; end; To copy the generated graph, you can use the following simple method:
procedure TGraph.copy (g : TGraph); // g var i,j : integer; begin for i:=1 to vertNum-1 do for j := 0 to i-1 do if g.isEdge (i,j) then addEdge (i,j); end; The search for test peaks also did not complicate (for detailed non-etude research on the Internet, you can find many good procedures for generating random graphs):
function TGraph.findTestPair : string; var i,j,maxV1,maxV2 : integer; maxLen : integer; begin maxLen := 0; maxV1 := 0; maxV2 := 0; for i := 1 to maxGen do begin testPairV1 := random (vertNum); // 1- j := 0; repeat testPairV2 := random (vertNum); // 2- inc (j); until ((testPairV1<>testPairV2) and (not isEdge (testPairV1, testPairV2))) or (j=maxGen); if BFSsp(testPairV1, testPairV2) then begin getShortestPath (testPairV1, testPairV2); if pathLen > maxLen then begin maxLen := pathLen; maxV1 := testPairV1; maxV2 := testPairV2; end; path := nil; end end; testPairV1 := maxV1; testPairV1 := maxV2; Result := 'Test vertex pair '+intToStr(testPairV1)+', '+ intToStr(testPairV2)+' Path length '+ intToStr(maxLen); end; The maxGen constant took 10, and then how lucky - not all generations are suitable. I will give one of the typical results:
--- Benchmark ---------
Vertex number: 3000 Edge number: 4000 Max degree: 4
TDirectedGraph: Test vertex pair 2671, 853 Path length 12
TDirectedGraph: shortest path 2671-2629-2646-1658-499-2625-354-1027-626-733-2641-853
Elapsed time: 0.0160002149641514 sec.
TUndirectedGraph: shortest path 2671-2629-2646-1658-499-2625-354-1027-626-733-2641-853
Elapsed time: 0.030999630689621 sec.
TBigUndirectedGraph: shortest path 2671-2629-2646-1658-499-2625-354-1027-626-733-2641-853
Elapsed time: 0.0470004742965102 sec.In other distributions, the time difference is even smaller, but the overall trend is
tTDirectedGraph leqslanttTUndirectedGraph leqslanttTBigUndirectedGraph,
Where t - time.
Thus, it can be assumed that, on the one hand, a change of presentation (from among those used) may not particularly affect speed, but, on the other hand, it is worth testing different ideas for a specific task and for the expected type of graphs. Specially emphasized the word "assume", because the results are too weak for more categorical recommendations. Another task can show qualitatively different results. It is probably impossible to make a choice of any one presentation for all cases. In connection with this, the following thought appears. Usually, programs like the described T program are used in the development of the library and at the final testing stage, but they do not reach the users. At the same time, in many large libraries you can find functions that do the same thing, but with data of different structure and different methods. I think that in such cases it will be very useful if developers apply tools to the libraries to help the user make an informed and informed choice. The next progressive step can be a program that, having received parameters from the user to generate the necessary tests, will make a choice of algorithms and data structures based on the results of these tests and give the user recommendations on the use of library resources. Depending on the task and on the support capabilities, tests can not only be generated, but also downloaded from a local database, from a support site or as a result of a global search on the Internet. In the test sample there may be columns with a feature that is not obvious to the customer. The tests automatically take into account this feature. It will be an intellectual (AI, maybe AI + natural intelligence) solution to the problem of choosing a representation, marked in the title of this etude.
Further more. Now, in order to find the right library, we type in the search engine something like “search for the shortest path in the graph”. Next, we hope for a miracle that will help of hundreds of thousands of links to find the most suitable for our case. If the libraries are equipped with T-programs with a standardized network protocol (you may need new protocols), the user could send a test suite to the search engine, and the T-program servers would run these tests. The search engine would analyze the results and, in response to a request, would provide links to the libraries most appropriate for the given case. At the same time, by sending requests, the search engine can take into account the results of similar previous requests. This will be a search for a new type. Now libraries receive ratings by the number of downloads, and in the case of such a search they will receive ratings on the satisfaction of users' test tasks. Ratings will be highly differentiated: in one group of requests there will be a priority of maximum performance, and in the other, memory savings, and in the third there may be an additional requirement of references only to free libraries, etc. Of course, a comparison of the results obtained on different servers will be very approximate, even with the use of correction factors for the computing capabilities of the server. A final comparison of the pre-selected options will need to be done on the client computer.
Now on the Internet you can find a bunch of various online calculators and file format converters - so it seems that you can count and convert anything online. , offline .
, , , . , ( «» ) . , :
adjMatrix : array of array of Byte; 1 , , 8 . , Cardinal (4 ), :
adjMatrix : array of array of Cardinal; .., .., , 38- « — 2014», . : , 2014, C. 432 . bsf (bit scan forward) CPU 17 . GPU (. ).
— :
adjMatrix : array [1..maxVertNum] of set of 1.. maxVertNum; : – . . , , , Delphi (maxVertNum) . . , . , , Pascal 8000 OS 360/370 – forall:
forall i in aSet do:
for i:=minI to maxI do if i in aSet then , – .
Source: https://habr.com/ru/post/339752/
All Articles