Expansion of analytical capabilities of the linear programming method with Python tools

Introduction

On linear programming with Python tools, I in the article [1] considered the solution of the optimization problem with the function of an alternative to the main goal. As was shown in the article, the reception with the introduction of new functions of the goal when considering a single general optimization problem significantly expands the analytical capabilities of the method. Therefore, it is logical to choose and consider an example in which when solving a general optimization problem one can formulate several alternative goal functions.

Formulation of the problem

Using the example of the optimal diet problem, consider the formation of various alternative goal functions with the necessary initial conditions. In addition, to develop a simple and uniform interface for solving such problems with the output of results that are understandable to the end user.

Formation of the objective function and initial conditions to minimize the cost of the diet

To maintain normal life, a person needs to consume at least 118 g of proteins, 56 g of fat, 500 g of carbohydrates and 28 g of mineral salts per day. These nutrients are contained in different quantities and different foods.
')
The table shows the amount of nutrients in various products in g / kg and the conditional price of these products for 1 kg. It is necessary to make a daily ration containing the minimum daily rate of nutrients at their minimum cost .



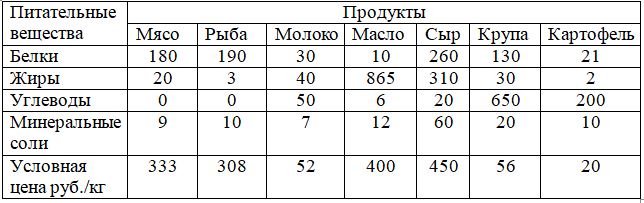
Denoting by: X1 is the amount of meat; X2 is the number of fish; X3 is the amount of milk; X4 is the amount of oil; X5 is the amount of cheese; X6 is the amount of cereals; X7 - the number of potatoes consumed by man per day. We can make an equation for the total cost of F nutrition per day:

F = 333 * X1 + 308 * X2 + 52 * X3 + 400 * X4 + 450 * X5 + 56 * X6 + 25 * X7

We need to find a minimum of F.

The total amount of proteins in the human diet should not be less than 118 g. Hence:

180 * X1 + 190 * X2 + 30 * X3 + 10 * X4 + 260 * X5 + 130 * X6 + 21 * X7≥118

We make the same inequalities for fats, carbohydrates and salts. We have:

20 * X1 + 3 * X2 + 40 * X3 + 865 * X4 + 310 * X5 + 30 * X6 + 2 * X7≥56
50 * X3 + 6 * X4 + 20 * X5 + 650 * X6 + 200 * X7≥500
9 * X1 + 10 * X2 + 7 * X3 + 12 * X4 + 60 * X5 + 20 * X6 + 10 * X7≥28

Solve the problem

from cvxopt.modeling import variable, op import time start = time.time() x = variable(7, 'x') z=(333*x[0] + 308*x[1] +52* x[2] +400*x[3] +450*x[4] +56* x[5]+20*x[6]) mass1 =(- (180*x[0] + 190*x[1] +30* x[2] +10*x[3] +260*x[4] +130* x[5]+21*x[6]) <= -118) mass2 =(- (20*x[0] + 3*x[1] +40* x[2] +865*x[3] +310*x[4] +30* x[5]+2*x[6]) <= -56) mass3 =(- (50* x[2] +6*x[3] +20*x[4] +650* x[5]+200*x[6]) <= -500) mass4 =(- (9*x[0] + 10*x[1] +7* x[2] +12*x[3] +60*x[4] +20* x[5]+10*x[6]) <= -28) x_non_negative = (x >= 0) problem =op(z,[mass1,mass2,mass3,mass4 ,x_non_negative]) problem.solve(solver='glpk') problem.status print(":") print(round(1000*x.value[0],1),'- ,  -',round(x.value[0]*333,1),'.') print(round(1000*x.value[1],1),'- ,  -',round(x.value[1]*308,1),'.') print(round(1000*x.value[2],1),'- ,  -',round(x.value[2]*52,1),'.') print(round(1000*x.value[3],1),'- ,  -',round(x.value[3]*400,1),'.') print(round(1000*x.value[4],1),'- ,  -',round(x.value[4]*450,1),'.') print(round(1000*x.value[5],1),'- ,  -',round(x.value[5]*56,1),'.') print(round(1000*x.value[6],1),'- ,  -',round(x.value[6]*25,1),'.') print(round(problem.objective.value()[0],1),"-      ") stop = time.time() print (" :",round(stop-start,3)) 

It should be noted some features of writing a program using the cvxopt module . Modeling: all variables are saved in lists, and list indices do not start from 1 , but from 0 ; in conditions that are written as non-strict inequalities, the upper limit must be set , therefore, to go from the lower limit, both parts of the inequalities are multiplied by -1 .

Result:

0.0-gram meat, costs - 0.0 rub.
0.0-gram of fish, costs - 0.0 rub.
0.0-milliliters of milk, costs - 0.0 rub.
38.0 - grams of oil, costs - 15.2 rubles.
-0.0 - gram cheese, costs - -0.0 rub.
679.3 - gram of cereals, costs - 38.0 rubles.
1395.9 - a gram of potatoes, costs - 34.9 rubles.
81.1 - the cost of one person per day
Time: 0.09

Formation of the objective function and initial conditions to minimize the calorie diet

For definiteness, let us suppose that we consider bread, meat, cheese, bananas, cucumbers, tomatoes, and grapes as the initial products — seven products in total. As nutrients - proteins, fat, carbohydrates.

The caloric value of one weight unit of each product is as follows: c1 = 2060, c2 = 2430, c3 = 3600, c4 = 890, c5 = 140, c6 = 230, c7 = 650.

The nutrient content in food is placed in the following table.



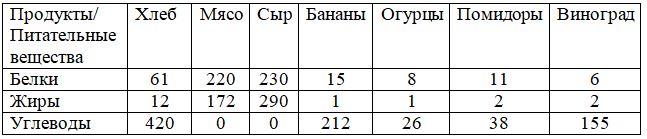
The minimum daily human need for nutrients is as follows: b1 = 100 in proteins, b2 = 70 in fats, b3 = 400 in carbohydrates.

Without reducing the generality of the problem to be solved, we can assume that the caloric content of food is measured in kilocalories / kg, the daily need for nutrients is in grams, and the nutrient content in foods is in grams / kg. Under these conditions, it becomes possible to perform additional verification of the formed conditions of the problem based on consideration of the physical dimension of the objective function and constraints.

Denoting by: x1 –the amount of bread; x2 is the amount of meat; x3 is the amount of cheese; x4 is the number of bananas; x5 is the number of cucumbers; x6 is the number of tomatoes; x7 is the amount of grapes consumed by man per day in kilograms.

We can make the equation of the total caloric intake F nutrition per day:

F = 2060 * x1 + 2430 * x2 + 3600 * x3 + 890 * x4 + 140 * x5 + 230 * x6 + 650 * x7

We need to find a minimum of F.

The total amount of proteins in the human diet should not be less than 100 g. Hence:

61 * x1 + 220 * x2 + 230 * x3 + 15 * x4 + 8 * x5 + 11 * x6 + 6 * x7 ≥100

We make the same inequalities for fats and carbohydrates. We have:

12 * x1 + 172 * x2 + 290 * x3 + 1 * x4 + 1 * x5 + 2 * x6 + 2 * x7 ≥70
420 * x1 + 0 * x2 + 0 * x3 + 212 * x4 + 26 * x5 + 38 * x6 + 155 * x7 ≥400

Solve the problem

 from cvxopt.modeling import variable, op import time start = time.time() x = variable(7, 'x') z=(333*x[0] + 308*x[1] +52* x[2] +400*x[3] +450*x[4] +56* x[5]+20*x[6]) mass1 =(- (180*x[0] + 190*x[1] +30* x[2] +10*x[3] +260*x[4] +130* x[5]+21*x[6]) <= -118) mass2 =(- (20*x[0] + 3*x[1] +40* x[2] +865*x[3] +310*x[4] +30* x[5]+2*x[6]) <= -56) mass3 =(- (50* x[2] +6*x[3] +20*x[4] +650* x[5]+200*x[6]) <= -500) mass4 =(- (9*x[0] + 10*x[1] +7* x[2] +12*x[3] +60*x[4] +20* x[5]+10*x[6]) <= -28) x_non_negative = (x >= 0) problem =op(z,[mass1,mass2,mass3,mass4 ,x_non_negative]) problem.solve(solver='glpk') problem.status print(":") print(round(1000*x.value[0],1),'- ') print(round(1000*x.value[1],1),'- ') print(round(1000*x.value[2],1),'- ') print(round(1000*x.value[3],1),'- ') print(round(1000*x.value[4],1),'- ') print(round(1000*x.value[5],1),'- ') print(round(1000*x.value[6],1),'- ') print(round(problem.objective.value()[0],1),"-     ") stop = time.time() print (" :",round(stop-start,3)) 

Result:

0.0 grams of bread
211.5 - grams of meat
109.4 grams of cheese
1886.8 - a gram of bananas
0.0 gram of cucumber
0.0-gram tomatoes
0.0 gram of grapes
2587.1 -kilokaloriya-calorie diet of one person per day
Time: 0.06

Formation of the objective function and initial conditions for minimizing the caloric content of the diet when recruiting products according to user preferences

We make a conditional set of products, for example only. We take the initial conditions for the caloric content of products from the solution of the previous problem.

The solution of the problem

 from cvxopt.modeling import variable, op import time start = time.time() x = variable(7, 'x') z=( x[0] + x[1] +x[2] +x[3] +x[4] +x[5]+x[6]) mass1 =(- (61*x[0] + 220*x[1] +230* x[2] +15*x[3] +8*x[4] +11* x[5]+6*x[6]) <= -100) mass2 =(- (12*x[0] +172*x[1] +290* x[2] +1*x[3] +1*x[4] +2* x[5]+2*x[6]) <= -70) mass3 =(- (420*x[0] +0*x[1] +0* x[2] +212*x[3] +26*x[4] +38* x[5]+155*x[6]) <= -400) mass4 =(-( 2060*x[0] + 2430*x[1] +3600* x[2] +890*x[3] +140*x[4] +230* x[5]+650*x[6]) <= -3000) x_non_negative = (x >= 0) problem =op(z,[mass1,mass2,mass3, mass4,x_non_negative]) problem.solve(solver='glpk') problem.status print(":") print(round(1000*x.value[0],1),'- ') print(round(1000*x.value[1],1),'- ') print(round(1000*x.value[2],1),'- ') print(round(1000*x.value[3],1),'- ') print(round(1000*x.value[4],1),'- ') print(round(1000*x.value[5],1),'- ') print(round(1000*x.value[6],1),'- ') print(round(problem.objective.value()[0],1),"--    \n     ") stop = time.time() print (" :",round(stop-start,3)) 

Result:

952.4 - grams of bread
0.0-gram meat
288.4 grams of cheese
0.0 grams of bananas
0.0 gram of cucumber
0.0-gram tomatoes
0.0 gram of grapes
1.2-kilogram-the total mass of products from
one person’s diet per day
Time: 0.051

I don’t comment on the results of problem solving due to obviousness. In addition, the initial data are conditional, and in the latter problem are individual.

Practical conclusions or why all this is necessary

The program interface is so simple and intuitive that it does not require any additional skills. It is enough to download and install the latest version of Python, for example, from the site [2], and the cvxopt library from the site [3]. Then create a file with the extension py and place in it any of the programs listed in the article, after modifying it for your task with the new goal function and restrictions.

Links

1. Solving the direct and dual problems of linear programming with Python tools.
2. Python.
3. Unofficial Windows Binaries for Python Extension Packages.