Mathematical model of a liquid tachometer in Python

Introduction

In the technique of the phenomenon of the formation of the surface of a rotating fluid in the form of rotation close to the surface of a paraboloid, it is used mainly in separating centrifuges to separate suspensions into fractions [1].

I was interested in the so-called liquid tachometer. The principle of operation of the device is to control the level of the upper edge of the liquid in a rotating cylindrical glass.
The liquid level depends on the speed of rotation of the glass and can be controlled by a simple optical tracking system.

Consideration of the mathematical model of such a device is not only informative, but also of practical interest, taking into account its implementation by means of the freely distributed general-purpose language Python.
')

Theory - simple and short

The vectors of forces acting on a fluid particle in a rotating cylindrical cup are shown in the following figure.



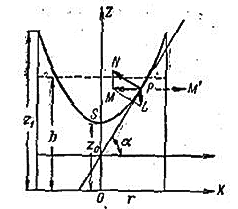
Consider the section of the surface of revolution by the coordinate plane ZX and find the tangent at the point P (x, z) of this section. The particle Q located at the point P is acted upon by gravity mg depicted as a vector PL.

The fluid pressure is depicted as a PN vector directed normally to the surface of the fluid. Forces PM and PM 'for steady motion are equal. A particle of fluid moves around a circle of radius x its acceleration PM is directed to the center of rotation and is equal to m * w ** 2 * x .

In the above formulas, w, m, g are the angular frequency, mass, and acceleration of gravity. In the right-angled triangle NMP, the angle at the vertex N is equal to the derivative dz / dx (we will use the Python syntax when writing formulas).

dz / dx = MP / NP = m * w ** 2 * x / mg = w ** 2 * x / g (1)

Integrating (1) we obtain the equation for the surface of the liquid in the section ZX. To integrate (1), we use the symbolic calculation of the indefinite integral using the SymPy module:

from sympy import * x,z,w,g = symbols('xzw g') print('z=',integrate(w**2*x/g, x),'+C') 

Under the “sign” of the indefinite integral, integrate (f (x), x) is the function f (x) = w ** 2 * x / g of the variable x. The remaining parts of the equality including the integration constant C are simply written as string variables.

Will get

z = w ** 2 * x ** 2 / (2 * g) + C (2)

The integration constant C is determined by substituting in (2) - x = 0 and z = z0, we obtain C = z0. On the upper edge of the rotating fluid x = R, where R is the radius of the cylinder, we rewrite (2) in the form:

z-z0 = w ** 2 * R ** 2 / (2 * g) (3)

In the stationary state, the fluid level is H, and its volume is V = pi * R ** 2 * H. When the fluid begins to rotate and after the motion becomes steady, the volume of the fluid does not change, and it will be equal to the volume counted from the upper edge of the fluid - pi * R ** 2 * z1 minus the volume occupied by the paraboloid of rotation.

This volume is equal to the product of the number pi by a definite integral in the range from z0 to z1 from the relation x ** 2 = 2 * g (z-z0) / w ** 2, obtained from (3) by the inverse substitution x = R.

We use the symbolic computation of a definite integral using the SymPy module:

  from sympy import * z,z0,z1,w,g = symbols('z z0 z1 w g') print ('pi*R**2*H=pi*R**2*z1 -pi*', factor(simplify(integrate(2*g*(z-z0)/w**2,(z,z0,z1))))) 

Under the “sign” of a definite integral, integrate (f (z), (z, z0, z1)) is the function f (z) = (2 * g * (z-z0) / w ** 2 and the tuple is (z, z0 , z1) with variable z and integration limits – z0, z1. Simplify the function to simplify the expression, and factor to collect in a full square. The remaining parts of the equation are simply written as string variables.

Will get

pi * R ** 2 * H = pi * R ** 2 * z1 -pi * g * (z0 - z1) ** 2 / w ** 2 (4)

After substitution (3) in (4) we get:
H = (z1 + z0) / 2 (5)
Solving (3) relative to the circular frequency of rotation w and eliminating, taking into account (5) the variable z0, we obtain the equation for the theoretical characteristic of the water tachometer:
w = 2 * sqrt (g * (z1-H)) / R (6)

The relation (6) shows only the nature of the dependence, the real characteristic is obtained during calibration.

R = 0.11 m., H = 0.09, we construct the theoretical characteristics of a liquid tachometer for the range z1 = 0.1 ÷ 0.16.

 from mpmath import * w=lambda z1: 2*sqrt (9.8*(z1-0.09))/0.1 plot (w,[0.1,0.16]) 

Using the mpmath function simplifies the visualization of numeric data.

Will get

3D Tachometer Model

The surface of a rotating fluid can be described by a paraboloid of rotation. In general, it is an elliptic paraboloid. It is determined by the following dependence of the coordinates of surface points on two parameters u and v:

x = a * u * cos v, y = b * u * cos v, z = 0.5 * u ** 2

In our case, the fluid is in a cylindrical cup, so a = b .

Result

The surface of a cylinder is determined by the following dependence of the coordinates of surface points on two parameters u and v:
x = a * cos v, y = a * sin v, z = u

Result

Place the paraboloid of rotation in the cylinder, so that the upper edge of the cylinder coincides with the edge of the paraboloid. In this case, with an increase in the frequency of rotation of the cylinder, the level of the upper edge of the liquid rises. Consider the operation of the liquid tachometer. We introduce the coefficient K , as a characteristic of the speed of rotation of the fluid in the next program.

  #!/usr/bin/env python #coding=utf8 import pylab from numpy import (zeros,arange,ones,pi,sin,cos) from mpl_toolkits.mplot3d import Axes3D def paraboloid(k): a=2 v = arange(0, 2.05*pi, 0.05*pi) u= zeros([len(v),1]) for i in arange(0,len(v)): u[i,0]=list(arange(0,2.05,0.05))[i] x=a*u*cos(v) y=a*u*sin(v) z=k*u**2*ones(len(v)) p=z[len(v)-1,len(v)-1] a=2*a u= zeros([len(v),1]) for i in arange(0,len(v)): u[i,0]=list(arange(-2.1,2.1,0.1))[i] X = a*ones(len(u))*cos(v) Y =a*ones(len(u))*sin(v) Z = u*ones(len(v)) q=Z[len(v)-1,len(v)-1] d=pq-0.1 Z = u*ones(len(v))+d fig = pylab.figure(num='     ') axes = Axes3D(fig) axes.set_xlabel('x') axes.set_ylabel('y') axes.set_zlabel('z') axes.plot_surface(x, y, z, rstride=1, cstride=1,color='red') axes.plot_surface(X, Y, Z, rstride=1, cstride=1, color='blue') pylab.show() for k in arange(0.2,0.7,0.2): print('k=',k) paraboloid (k) 

To connect the cylinder and the paraboloid of rotation, the following lines of the program for redefining the coordinate of the cylinder Z according to the coordinate of the paraboloid z are used:

 q=Z[len(v)-1,len(v)-1] d=pq-0.1 Z = u*ones(len(v))+d 

Result

k = 0.2


k = 0.4


k = 0.6

In addition to the coefficient K, the model allows you to set the required radius of the cylinder R and the level of liquid in the cylinder H.

findings

The resulting mathematical model can be applied not only in the design of a liquid tachometer, but also in the development of an automatic dispenser, since the volume of liquid displaced by a paraboloid of rotation can merge through the holes in the cylinder. In addition, the use of Python will expand the use of the mathematical model.

Links

1. Centrifuge. Centrifuging process.