Numbers - Douglas Crockford’s paper on number systems in life and in programming
Now computers solve almost any problems. They work and benefit in almost all industries. But let's see what a computer is. This is a machine that manipulates numbers. Such manipulations are practically all that they can do. Therefore, the fact that they solve so many problems just by manipulating numbers seems almost magical.
Let's see where the numbers came from, where they can lead and how they work.
')
The article is based on the report of Douglas Crockford (Douglas Crockford) from the June conference of HolyJS 2017 in St. Petersburg (the presentation of the report can be found here )
Let's start with the fingers. Fingers are much older than numbers. The man has developed fingers to better climb trees and collect fruit. And he was really happy doing this for millions of years.
But the climate has changed, the trees began to disappear. The man had to go down to the ground, go over the grass and look for other sources of food. And fingers were needed to manipulate tools, such as a stick. With its help, it was possible to dig the ground to find tubers. Another example of a tool is a stone that allows you to bang tubers to make them soft enough to eat (our little monkey teeth do not allow us to eat everything; to survive, we were forced to learn how to cook).
Over time, people gained experience in handling tools. And the tools influenced our evolution, so we continued to update them. Soon we learned how to make knives of volcanic glass, and eventually learned how to control the fire. Now, man knew how to plant seeds in the ground and grow his own food. With new knowledge, people began to gather in larger communities. We have moved from families and clans to cities and nations.
Society grew, and the problem of tracking all human activity. To solve it, a man had to come up with an account.
As it turned out, our brain does not remember a lot of numbers very well. But the more complex the society became, the more it was necessary to memorize. Therefore, man learned to make notches on wood and graffiti. There were ideas to string nuts on strings. But we still forgot what exactly these numbers are. Therefore it was necessary to invent writing.
Today we use writing to solve many problems: for letters, for laws, for literature. But first they were manuscripts. I consider the invention of writing to be the most important discovery ever made by man, and it happened three times.
The first traces of writing were found in the Middle East. Many smart people believe that this happened in Mesopotamia. I think it happened in Egypt. In addition, writing was invented in China and in America. Unfortunately, the last of these civilizations did not survive the Spanish invasion.
Let's take a closer look at some historical number systems.
It looked like the numbers in Egypt.

The Egyptians had a decimal system. For each degree 10 they had their own hieroglyph. The stick represented a unit, a piece of rope - 100, a finger - 10,000, and a guy with his hands up - a million (this demonstrates some mathematical sophistication, because they had a symbol denoting an abstract concept of "many", but exactly "million" no more, no less).
The Egyptians came up with many other things: a 3-by-4-by-5 triangle with a right angle (they knew why this angle was needed), a really smart system for working with fractions. They had an approximation for the number Pi and a lot more.
The Egyptians taught their system to the Phoenicians, who lived in the territory of modern Lebanon. They were very good navigators and traders — they sailed all over the Mediterranean and parts of the Atlantic. Having adopted a rather complicated number system from the Egyptians, they simplified it. Using writing consisting only of consonants, they reduced the character set from the thousands that the Egyptians had to a couple of dozen, which was much easier to use. And they taught their system to the people with whom they traded, in particular, the Greeks.
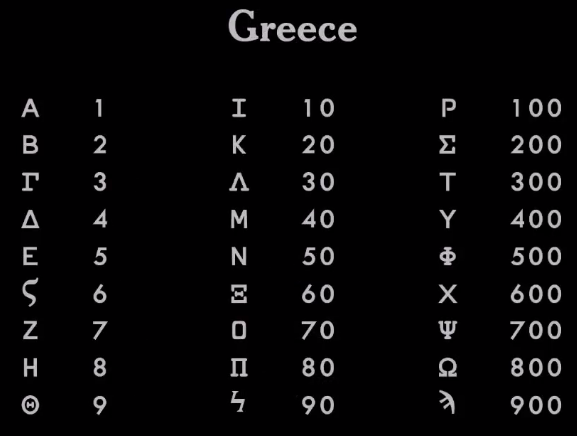
The Greeks took the Phoenician system and improved it by adding vowels. So now they could correctly spell all the words. Since then, the Greek alphabet contains 27 letters.
The Greeks used the same set of characters to write numbers. They took the first 9 letters of the alphabet to designate numbers 1 through 9, the next 9 letters for tens from 10 to 90, and another 9 letters for hundreds from 100 to 900. They transferred their system to the Romans.

But the Romans continued to use the Egyptian system as their basis. Although they adopted the Greek approach - the use of letters instead of hieroglyphs. They also added some innovations to make the numbers a bit more compact.
One of the problems of the Egyptian system was that writing a number 99 required a sequence of 18 characters. The Romans wanted to shorten the record. To do this, they came up with symbols representing half a ten or half a hundred (thousands). One of them was represented by the symbol I (or a stick), 10 - X (a bundle of sticks joined together), and 5 - V, which is only X in half.
Another innovation was the addition of subtraction to the number system. Until now, systems have been additive. The number was the sum of all the characters. But the Romans realized the idea that certain characters (in certain positions) could reduce the number.
Meanwhile, really interesting things were happening in China.
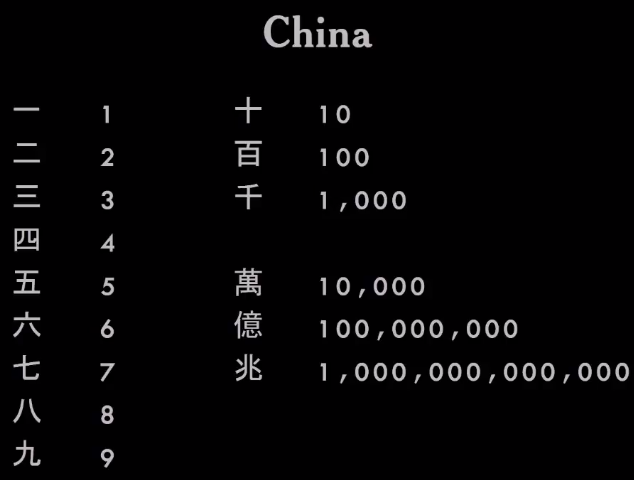
They had another system that used symbols from 1 to 9 and a set of multipliers or modifiers. So it was possible to record numbers of any size and complexity, just making up the hieroglyphs together. Very elegant system.
The biggest jump occurred in India.

Mathematicians in India came up with the idea of zero - a number that represented nothing. And they guessed to use it on a positional basis. Only 10 characters were used to display numbers, but they could be combined to create any number. This was a really important idea.
The Indians transferred their system to the Persians. Those called it Indian numbers. And from the Persians, the idea came to the Arabs. In turn, the Arabs handed it over to the Europeans, who called this method of writing Arabic numerals. This is the basic number system that most of the world uses today.
Really great is that no matter what language you speak, you can understand these numbers. Writing a number is as versatile as human communication.
Here is the same number recorded in all the systems mentioned.

And all these systems worked. They have been used by key nations and empires for centuries. Therefore, it is difficult to argue that one of these systems is better than the other.
The only advantage that the Indian system had over all the others was that it was possible to take a column of numbers and put them together without using scores - with just a pen, paper and a slightly trained brain. It was not easy to do in any other system.
Today it doesn't matter, since we have computers. Therefore, there is no clear answer to why we still use this system. Perhaps there are some advantages of its use, which I can not imagine, for example, in dialing a phone number. It seems that with the use of Roman numerals it will be quite difficult to do. But I do not remember when I last dialed the phone number. So perhaps it doesn't matter anymore.
An important idea is that the Indian numbers taught us mathematics.

This is a positional system. You can take the numbers and put them on the number line, and then add up the numbers in each position, multiplying them by 10 to the power corresponding to the number of this position. It turns out that Indian numbers are abbreviations for polynomials. A polynomial is a really important concept in mathematics. We got a way to write numbers. It was not in other systems.
This system also allowed for negative numbers.

We could write down the number with a minus sign, presenting negative things. This concept was meaningless in other number systems. We could not talk about the negative in Egypt, it did not make sense. But we can do it in the Indian system. And it turns out there are a lot of interesting things happening with negative numbers.
We can take a number series and continue it in the opposite direction to infinity. Using such a record, we get real numbers.

Other number systems could also work with fractions. But these have always been special cases. With the Indian system, we can write fractions in the same way as whole numbers — only a small discipline in managing decimal places is needed.
The original Indian entry indicated the position of the delimiter using the line on top.

But over the years, the separator symbol has changed.
Different countries have their own agreements on how to write. In some cultures, a decimal point is used, in others - a comma. And it didn't matter for a long time. You were in your country and could write numbers right or wrong. But it becomes a problem when you have the Internet, because now the numbers are everywhere. The number you write can be seen anywhere. And everyone will see different things - confusion may arise.

For example, depending on where you are and how you studied, you can read the first number in the picture as 2048 or 2 and 48 thousandths. And this may be a really serious mistake, especially when it comes to finances.
Therefore, I predict that the world will sooner or later find a way to choose one of the recording options. Because there is no value in this confusion. However, the difficulty in choosing one of the options is that none of them is clearly the best. How will the world choose?
I predict that you decide. And you choose the decimal point because your programming language uses it. And all the numbers in the world ultimately pass through computer programs. In the end, you just decide to simplify it.
All the above systems have a base of 10. So recorded numbers in the Middle East and China. They did not communicate with each other, but took the base 10.
How did this happen? They simply counted the fingers on both hands. And it worked.
But there are other cultures that recorded numbers differently. For example, in America there was a number system with a base of 20. Do you know how they thought of it? I think this is obvious: they counted the fingers not only on the arms, but also on the legs. And it worked too. They had a developed civilization. They did a lot of calculations, but they used base 20.
Some cultures used base 12. And we can still see their footprints in our world. For example, our watch has a base of 12. We still have 12 inches in feet. We have learned this from the British and still can not refuse to use such complications.
The Sumerians used base 60. Yes, and we still stick to base 60, right? We consider our time this way and make geographical measurements. Geographical applications have to use a coordinate system based on the number system with a base of 60. This adds unnecessary complexity.
How did base 60 come about? I think when the cities grew, they absorbed many small settlements, combining them into large ones. At some point, they tried to unite the community that used base 10 with the community that took as base 12. Surely there was some kind of king or committee — someone had to decide how to unite them. The correct option was to use base 10. The second option was to develop with base 12. But instead they chose the worst possible option - they used a base that is the least common multiple. The reason this decision was made is that the committee could not decide which of the options is better. They came to a compromise, which, in their opinion, is similar to what everyone wanted. But it's not about who wants what.
It should be noted that the committees still make such decisions every time standards are issued.
The really interesting thing about the base is the appearance of the binary system. We can take the Indian system and simply replace 10 with 2.

So we can represent everything with the help of bits. And it was a really important step forward, because it allowed me to invent a computer.
If we start talking about computers using binary format, we need to remember about the sign of the number. Record and display the sign in three ways:
Each of the options has its drawbacks, in particular, some additional numbers. I think we should take this additional number (negative 0 or additional negative number from the second addition) and turn it into a signal that this is not a number at all. Thus, it will allow us to avoid a problem that manifests itself in Java: if we use the indexOf method to find a string in another string, and if it does not find it, Java cannot signal it. Because this stupid system can only return an int, and an int can only represent integers.
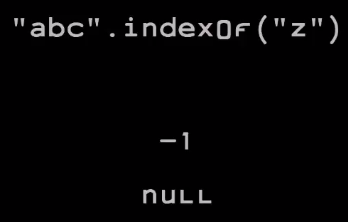
To get around this problem, they invented a dubious compromise: return minus one. But unfortunately, if you just take the return value and put it in a different formula, you can get the wrong result. If the method returned a null value, this could be detected in the downstream, and we were less likely to get a bad result of the calculation.
Let's take a closer look at the types used in our languages.
We have many languages where there is an int32 under different names. If we add two int32 numbers, which type will the result be? The answer is int33, because as a result of the addition you can get a number that is slightly larger than int32.
Java is wrong here. Java says it is an int32.
Another example is the multiplication of int32 by int32. What do we get as a result? It looks like int63.

When, as a result of the usual calculation, a result is obtained that goes beyond the type, we get an overflow. And our CPUs know about it. For example, in the Intel architecture, there is a carry flag in the CPU that contains this 33rd bit. Also on Intel architecture, if you multiply 32-bit numbers, you get a 64-bit result. Those. a register is provided that contains the “extra” 32 bits you need. And there is an overflow flag that is set if you want to ignore the high order of multiplication. He reports that an error has occurred. Unfortunately, Java does not allow you to receive this information. She simply discards everything that is a problem.
What should happen in case of overflow? There are several options for action:
If you intend to maximize the number of possible errors, you simply discard the most important bits without notice. This is what Java and most of our programming languages do. Those. they are intended to increase the number of errors.
The first computers worked with integers. But the machines were built and programmed by mathematicians, and they wanted to work with real numbers. Therefore, arithmetic was developed, where a real number is represented as an integer multiplied by a certain scale factor.
If you have two numbers with the same scaling factors, you can simply add them, and if they have different scale factors, to perform the simplest operations you will have to change at least one of them. Therefore, before performing any operations, it is necessary to compare the scale factor. And the recording became a bit more difficult, because at the end you had to put an excess scale factor. And the division has become more complicated because you have to consider the scaling factor. As a result, people began to complain that it made programming really difficult, very error-prone. In addition, it was difficult to find the optimal scale factor for any application.
As a solution to these problems, someone suggested making floating-point numbers that could display approximated real numbers using two components: the number itself and a record of where the decimal separator is located inside it.
Using such a record, it is relatively easy to do addition and multiplication. So you get the best results that the machine can provide, using far less programming. It was a great achievement.
The first form of writing a floating-point number looks like this: we have a number, the value of which is increased by 10 to the power of the logarithm of the scale factor.

This approach was implemented in the software of the first machines. He worked, but extremely slowly. The cars themselves were very slow, and all these transformations only worsened the situation. Not surprisingly, there is a need to integrate it into iron. The next generation of machines already at the hardware level understood floating point computations, albeit for binary numbers. The transition from decimal to binary system was caused by a performance loss due to division by 10 (which must sometimes be done to normalize numbers). In the binary system, instead of dividing, it was enough just to move the separator - it is practically “free”.
Here is the binary standard for floating-point computing:
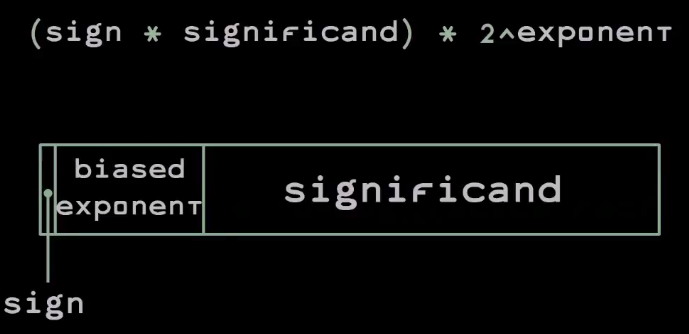
The number is written with a bit of the sign of the mantissa, which is 0 if the number is positive, and 1 if negative, the mantissa itself, as well as the biased exponent. The offset in this case plays the role of a small optimization - due to it, you can perform an integer comparison of two floating point values to see which one is greater.
However, there is a problem with this record: in it, 0.1 + 0.2 is not equal to 0.3.

The result is close, but it is wrong.
Let's see what happens.

Imagine a numerical series. 0.1 is approximately 1/16 + 1/32, but a bit more, so we will need a few more bits. As we move along the number row, we get an infinitely repeating series 0011, similar to what happens with 1/3 in decimal.

This is great if you have an infinite number of bits in stock. If you continue this sequence to infinity, get exactly what you need. But we do not have an infinite number of bits. At some point we have to cut off this tail. And from where you cut, will depend on the final error.
If you cut off before 0, you will lose all subsequent bits. Therefore, your result will be slightly less than necessary. If you cut off before 1, according to the rounding rules, you must move the unit, then the result will be slightly more.

And you can hope that in the course of the calculations you will make a little mistake in one and the other direction, and as a result the errors will be balanced. But this is not happening. Instead, the error accumulates - the more calculations we do, the worse the result.
Whenever we represent a constant in a program written in some language or in data as a decimal, we do not get that particular number. We get an approximation of this number, because we work with a numerical system that cannot accurately represent decimals. And this violates the associative law.
Associative law is really important in the course of algebraic manipulation of expressions in programs. But it is not respected if the inputs / outputs and intermediate results of the calculations cannot be accurately represented.
And since none of our numbers are represented exactly, all calculations are wrong! This means that (A + B) + C is not the same as A + (B + C), and the order in which you perform the calculations can change the result.
This problem is not new. It was known when the floating-point calculations in the binary system were developed — the developers thus made a compromise.
At that time there were two schools of computation:

Computers are getting cheaper, and now they solve almost any problems, but we are still stuck in this template with two different worlds.
Another problem in representing a floating point number in binary format is the complexity of text conversion. Take a piece of text and turn it into a number; then take a number and convert it back to a piece of text. This should be done correctly, efficiently and without surprises, using as few numbers as possible. It turns out that such a record is a very difficult problem, expensive in terms of performance.
In most modern programming languages there is confusion due to erroneous data types. For example, if you write in Java, each time creating a variable, property or parameter, you need to choose the right type from Bite, Char, Short, Int, Long, Float, Double. And if you choose wrong, the program may not earn. And the error does not appear immediately, and in the tests it will not be visible. It will show itself in the future when overflow occurs and the bad things associated with it.
What can happen? One of the most impressive examples was the failure of the Aryan 5. This is a rocket sent by the European Space Agency. She strongly deviated from the course, and then exploded a few seconds after the start. The reason for this was a bug in software written in Hell. Here I translated the error to Java:

They had a variable defining the horizontal offset. And she was transferred to Short, which overflowed. The result, caught in Short, was wrong. But he was sent to the guidance system and completely confused, so that the course could not be restored. This error is estimated at about half a billion dollars.
I believe that you have not yet made mistakes that would cost half a billion dollars. But could (technically it is still possible). Therefore, we should try to create recording systems and languages to avoid such problems.
From the point of view, the choice of data type when declaring JavaScript variables is much better - this language has only one numeric type. This means that a whole class of errors can be automatically avoided. The only problem is that this type is incorrect, as these are floating point binary numbers. And we need floating-point decimal numbers, since sometimes we add up the money and we want the result to make sense.
I propose to correct this type. My correction is called DEC64, which is a modern entry for decimal floating point numbers. I recommend DEC64 as the only numerical type in future application languages. Because if you only have one numeric type, you cannot make a mistake by choosing the wrong type (I think this will provide much more value, something that we can get by having several types).
The hardware implementation of DEC64 allows you to add numbers in one cycle, which reduces the importance of performance when using the old types. The advantage of DEC64 is that in this recording, the basic operations on numbers work the way people are used to. And eliminating numeric confusion reduces errors. In addition, converting DEC64 numbers to text and vice versa is simple, efficient, and free of surprises. In fact, it is a bit more complicated than converting integers to text and back - you just need to keep track of where the decimal point is, and you can remove excess zeros from both ends, and not just from one.
DEC64 can accurately represent decimal fractions containing up to 16 digits, which is enough for most of our applications. You can represent numbers from 1 * 10 -27 to 3 with 143 zeros.
DEC64 is very similar to floating point source numbers developed in the 40s. The number is represented as two numbers that are packed into a 64-bit word. The ratio is represented by 56 bits, and the rate is 8 bits.
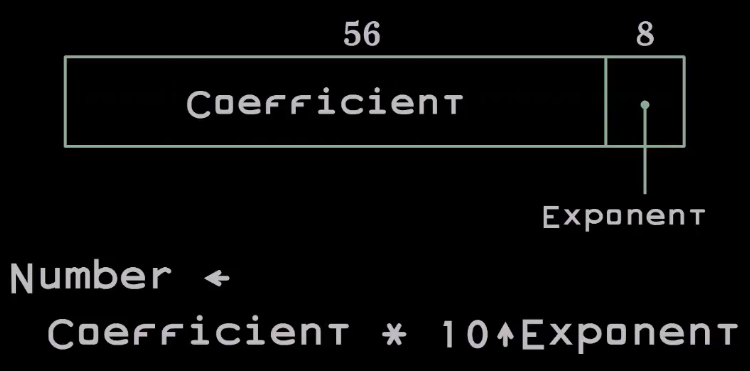
The reason why the exhibitor is at the end is that, in the Intel architecture, we can unpack this number almost for free. This helps in the implementation of the software.
If you want to look at the software implementation of DEC64, you can find it on GitHub . , DEC64 .
DEC64 JavaScript, . , , . DEC64 ( , JavaScript — ; - ).
= .
0/0?
, 0 * n n.
, 0. , , 0, . . , , , n NaN, 0 x NaN .
?
, : , , — , - .
, . , . , , , . . , (), — 0 1, ( ). , , . 0 (, , ) .
DEC64, .
, .

. XII , — , , . , 1202 . . , , .

, . , , 2 . , . .

— , , — true false. .

— . : -, , . . -, , , . : , .. .

, , . , , .
. — -, , , . .
, . . , . . .
? , . -, , . , . -, , . , .
— . .
, HolyJS 2017 Moscow , 10 11 .
Let's see where the numbers came from, where they can lead and how they work.
')
The article is based on the report of Douglas Crockford (Douglas Crockford) from the June conference of HolyJS 2017 in St. Petersburg (the presentation of the report can be found here )
Fingers
Let's start with the fingers. Fingers are much older than numbers. The man has developed fingers to better climb trees and collect fruit. And he was really happy doing this for millions of years.
Instruments
But the climate has changed, the trees began to disappear. The man had to go down to the ground, go over the grass and look for other sources of food. And fingers were needed to manipulate tools, such as a stick. With its help, it was possible to dig the ground to find tubers. Another example of a tool is a stone that allows you to bang tubers to make them soft enough to eat (our little monkey teeth do not allow us to eat everything; to survive, we were forced to learn how to cook).
Over time, people gained experience in handling tools. And the tools influenced our evolution, so we continued to update them. Soon we learned how to make knives of volcanic glass, and eventually learned how to control the fire. Now, man knew how to plant seeds in the ground and grow his own food. With new knowledge, people began to gather in larger communities. We have moved from families and clans to cities and nations.
Society grew, and the problem of tracking all human activity. To solve it, a man had to come up with an account.
Score
As it turned out, our brain does not remember a lot of numbers very well. But the more complex the society became, the more it was necessary to memorize. Therefore, man learned to make notches on wood and graffiti. There were ideas to string nuts on strings. But we still forgot what exactly these numbers are. Therefore it was necessary to invent writing.
Writing
Today we use writing to solve many problems: for letters, for laws, for literature. But first they were manuscripts. I consider the invention of writing to be the most important discovery ever made by man, and it happened three times.
The first traces of writing were found in the Middle East. Many smart people believe that this happened in Mesopotamia. I think it happened in Egypt. In addition, writing was invented in China and in America. Unfortunately, the last of these civilizations did not survive the Spanish invasion.
Let's take a closer look at some historical number systems.
Egypt
It looked like the numbers in Egypt.

The Egyptians had a decimal system. For each degree 10 they had their own hieroglyph. The stick represented a unit, a piece of rope - 100, a finger - 10,000, and a guy with his hands up - a million (this demonstrates some mathematical sophistication, because they had a symbol denoting an abstract concept of "many", but exactly "million" no more, no less).
The Egyptians came up with many other things: a 3-by-4-by-5 triangle with a right angle (they knew why this angle was needed), a really smart system for working with fractions. They had an approximation for the number Pi and a lot more.
Phenicia
The Egyptians taught their system to the Phoenicians, who lived in the territory of modern Lebanon. They were very good navigators and traders — they sailed all over the Mediterranean and parts of the Atlantic. Having adopted a rather complicated number system from the Egyptians, they simplified it. Using writing consisting only of consonants, they reduced the character set from the thousands that the Egyptians had to a couple of dozen, which was much easier to use. And they taught their system to the people with whom they traded, in particular, the Greeks.
Greece

The Greeks took the Phoenician system and improved it by adding vowels. So now they could correctly spell all the words. Since then, the Greek alphabet contains 27 letters.
The Greeks used the same set of characters to write numbers. They took the first 9 letters of the alphabet to designate numbers 1 through 9, the next 9 letters for tens from 10 to 90, and another 9 letters for hundreds from 100 to 900. They transferred their system to the Romans.
Rome

But the Romans continued to use the Egyptian system as their basis. Although they adopted the Greek approach - the use of letters instead of hieroglyphs. They also added some innovations to make the numbers a bit more compact.
One of the problems of the Egyptian system was that writing a number 99 required a sequence of 18 characters. The Romans wanted to shorten the record. To do this, they came up with symbols representing half a ten or half a hundred (thousands). One of them was represented by the symbol I (or a stick), 10 - X (a bundle of sticks joined together), and 5 - V, which is only X in half.
Another innovation was the addition of subtraction to the number system. Until now, systems have been additive. The number was the sum of all the characters. But the Romans realized the idea that certain characters (in certain positions) could reduce the number.
China
Meanwhile, really interesting things were happening in China.

They had another system that used symbols from 1 to 9 and a set of multipliers or modifiers. So it was possible to record numbers of any size and complexity, just making up the hieroglyphs together. Very elegant system.
India
The biggest jump occurred in India.

Mathematicians in India came up with the idea of zero - a number that represented nothing. And they guessed to use it on a positional basis. Only 10 characters were used to display numbers, but they could be combined to create any number. This was a really important idea.
Idea replication
The Indians transferred their system to the Persians. Those called it Indian numbers. And from the Persians, the idea came to the Arabs. In turn, the Arabs handed it over to the Europeans, who called this method of writing Arabic numerals. This is the basic number system that most of the world uses today.
Really great is that no matter what language you speak, you can understand these numbers. Writing a number is as versatile as human communication.
Record numbers and math
Here is the same number recorded in all the systems mentioned.

And all these systems worked. They have been used by key nations and empires for centuries. Therefore, it is difficult to argue that one of these systems is better than the other.
The only advantage that the Indian system had over all the others was that it was possible to take a column of numbers and put them together without using scores - with just a pen, paper and a slightly trained brain. It was not easy to do in any other system.
Today it doesn't matter, since we have computers. Therefore, there is no clear answer to why we still use this system. Perhaps there are some advantages of its use, which I can not imagine, for example, in dialing a phone number. It seems that with the use of Roman numerals it will be quite difficult to do. But I do not remember when I last dialed the phone number. So perhaps it doesn't matter anymore.
An important idea is that the Indian numbers taught us mathematics.

This is a positional system. You can take the numbers and put them on the number line, and then add up the numbers in each position, multiplying them by 10 to the power corresponding to the number of this position. It turns out that Indian numbers are abbreviations for polynomials. A polynomial is a really important concept in mathematics. We got a way to write numbers. It was not in other systems.
Whole numbers
This system also allowed for negative numbers.

We could write down the number with a minus sign, presenting negative things. This concept was meaningless in other number systems. We could not talk about the negative in Egypt, it did not make sense. But we can do it in the Indian system. And it turns out there are a lot of interesting things happening with negative numbers.
Real Numbers
We can take a number series and continue it in the opposite direction to infinity. Using such a record, we get real numbers.

Other number systems could also work with fractions. But these have always been special cases. With the Indian system, we can write fractions in the same way as whole numbers — only a small discipline in managing decimal places is needed.
The original Indian entry indicated the position of the delimiter using the line on top.

But over the years, the separator symbol has changed.
Different countries have their own agreements on how to write. In some cultures, a decimal point is used, in others - a comma. And it didn't matter for a long time. You were in your country and could write numbers right or wrong. But it becomes a problem when you have the Internet, because now the numbers are everywhere. The number you write can be seen anywhere. And everyone will see different things - confusion may arise.

For example, depending on where you are and how you studied, you can read the first number in the picture as 2048 or 2 and 48 thousandths. And this may be a really serious mistake, especially when it comes to finances.
Therefore, I predict that the world will sooner or later find a way to choose one of the recording options. Because there is no value in this confusion. However, the difficulty in choosing one of the options is that none of them is clearly the best. How will the world choose?
I predict that you decide. And you choose the decimal point because your programming language uses it. And all the numbers in the world ultimately pass through computer programs. In the end, you just decide to simplify it.
Base
All the above systems have a base of 10. So recorded numbers in the Middle East and China. They did not communicate with each other, but took the base 10.
How did this happen? They simply counted the fingers on both hands. And it worked.
But there are other cultures that recorded numbers differently. For example, in America there was a number system with a base of 20. Do you know how they thought of it? I think this is obvious: they counted the fingers not only on the arms, but also on the legs. And it worked too. They had a developed civilization. They did a lot of calculations, but they used base 20.
Some cultures used base 12. And we can still see their footprints in our world. For example, our watch has a base of 12. We still have 12 inches in feet. We have learned this from the British and still can not refuse to use such complications.
Compromises: 60
The Sumerians used base 60. Yes, and we still stick to base 60, right? We consider our time this way and make geographical measurements. Geographical applications have to use a coordinate system based on the number system with a base of 60. This adds unnecessary complexity.
How did base 60 come about? I think when the cities grew, they absorbed many small settlements, combining them into large ones. At some point, they tried to unite the community that used base 10 with the community that took as base 12. Surely there was some kind of king or committee — someone had to decide how to unite them. The correct option was to use base 10. The second option was to develop with base 12. But instead they chose the worst possible option - they used a base that is the least common multiple. The reason this decision was made is that the committee could not decide which of the options is better. They came to a compromise, which, in their opinion, is similar to what everyone wanted. But it's not about who wants what.
It should be noted that the committees still make such decisions every time standards are issued.
Binary system
The really interesting thing about the base is the appearance of the binary system. We can take the Indian system and simply replace 10 with 2.

So we can represent everything with the help of bits. And it was a really important step forward, because it allowed me to invent a computer.
If we start talking about computers using binary format, we need to remember about the sign of the number. Record and display the sign in three ways:
- Signed magnitude representation. In this case, we simply add an extra binary bit to the number and decide in which of the states this bit corresponds to a positive number and in which to a negative one. It doesn't matter if we put this bit in front or behind (this is just a matter of convention). The disadvantage of this method is the presence of two zeros: positive and negative, which does not make sense, since zero has no sign.
- The first addition (One's complement) in which we perform the bitwise operation is not for the number to make it negative. In addition to the two zeros (positive and negative - as in the previous version), this representation has a transfer problem: in the usual addition of two numbers presented in this way, to get the correct result, you need to add 1 bit at the end. But otherwise it works.
- The second addition (Two's complement), which managed to get around the problem of transfer. Negative N is not a bit-negative negation of positive N, but + 1. In addition to the absence of a transfer problem, we get only one zero, which is very good. But at the same time we get an additional negative number. And this is a problem, because you cannot get the absolute value of this number — instead you get the same negative number. This is a potential source of error.
Each of the options has its drawbacks, in particular, some additional numbers. I think we should take this additional number (negative 0 or additional negative number from the second addition) and turn it into a signal that this is not a number at all. Thus, it will allow us to avoid a problem that manifests itself in Java: if we use the indexOf method to find a string in another string, and if it does not find it, Java cannot signal it. Because this stupid system can only return an int, and an int can only represent integers.

To get around this problem, they invented a dubious compromise: return minus one. But unfortunately, if you just take the return value and put it in a different formula, you can get the wrong result. If the method returned a null value, this could be detected in the downstream, and we were less likely to get a bad result of the calculation.
Types
Let's take a closer look at the types used in our languages.
int
We have many languages where there is an int32 under different names. If we add two int32 numbers, which type will the result be? The answer is int33, because as a result of the addition you can get a number that is slightly larger than int32.
Java is wrong here. Java says it is an int32.
Another example is the multiplication of int32 by int32. What do we get as a result? It looks like int63.

When, as a result of the usual calculation, a result is obtained that goes beyond the type, we get an overflow. And our CPUs know about it. For example, in the Intel architecture, there is a carry flag in the CPU that contains this 33rd bit. Also on Intel architecture, if you multiply 32-bit numbers, you get a 64-bit result. Those. a register is provided that contains the “extra” 32 bits you need. And there is an overflow flag that is set if you want to ignore the high order of multiplication. He reports that an error has occurred. Unfortunately, Java does not allow you to receive this information. She simply discards everything that is a problem.
What should happen in case of overflow? There are several options for action:
- we can keep the value null, which I think is very reasonable;
- or the maximum possible part (saturation - saturation). This may be reasonable in signal processing and in computer graphics. However, you do not want to do so in financial applications;
- it is possible to give an error - the machine should raise an exception or something should happen. The software should understand that there was confusion in the calculations and the need to rectify the situation;
- some say the program should stop. This is a rather harsh reaction, but this option would work if the machine did not just stop, but somehow reported that something was wrong.
If you intend to maximize the number of possible errors, you simply discard the most important bits without notice. This is what Java and most of our programming languages do. Those. they are intended to increase the number of errors.
Splitting numbers into values from different registers
The first computers worked with integers. But the machines were built and programmed by mathematicians, and they wanted to work with real numbers. Therefore, arithmetic was developed, where a real number is represented as an integer multiplied by a certain scale factor.
If you have two numbers with the same scaling factors, you can simply add them, and if they have different scale factors, to perform the simplest operations you will have to change at least one of them. Therefore, before performing any operations, it is necessary to compare the scale factor. And the recording became a bit more difficult, because at the end you had to put an excess scale factor. And the division has become more complicated because you have to consider the scaling factor. As a result, people began to complain that it made programming really difficult, very error-prone. In addition, it was difficult to find the optimal scale factor for any application.
As a solution to these problems, someone suggested making floating-point numbers that could display approximated real numbers using two components: the number itself and a record of where the decimal separator is located inside it.
Using such a record, it is relatively easy to do addition and multiplication. So you get the best results that the machine can provide, using far less programming. It was a great achievement.
The first form of writing a floating-point number looks like this: we have a number, the value of which is increased by 10 to the power of the logarithm of the scale factor.

This approach was implemented in the software of the first machines. He worked, but extremely slowly. The cars themselves were very slow, and all these transformations only worsened the situation. Not surprisingly, there is a need to integrate it into iron. The next generation of machines already at the hardware level understood floating point computations, albeit for binary numbers. The transition from decimal to binary system was caused by a performance loss due to division by 10 (which must sometimes be done to normalize numbers). In the binary system, instead of dividing, it was enough just to move the separator - it is practically “free”.
Here is the binary standard for floating-point computing:

The number is written with a bit of the sign of the mantissa, which is 0 if the number is positive, and 1 if negative, the mantissa itself, as well as the biased exponent. The offset in this case plays the role of a small optimization - due to it, you can perform an integer comparison of two floating point values to see which one is greater.
However, there is a problem with this record: in it, 0.1 + 0.2 is not equal to 0.3.

The result is close, but it is wrong.
Let's see what happens.

Imagine a numerical series. 0.1 is approximately 1/16 + 1/32, but a bit more, so we will need a few more bits. As we move along the number row, we get an infinitely repeating series 0011, similar to what happens with 1/3 in decimal.

This is great if you have an infinite number of bits in stock. If you continue this sequence to infinity, get exactly what you need. But we do not have an infinite number of bits. At some point we have to cut off this tail. And from where you cut, will depend on the final error.
If you cut off before 0, you will lose all subsequent bits. Therefore, your result will be slightly less than necessary. If you cut off before 1, according to the rounding rules, you must move the unit, then the result will be slightly more.

And you can hope that in the course of the calculations you will make a little mistake in one and the other direction, and as a result the errors will be balanced. But this is not happening. Instead, the error accumulates - the more calculations we do, the worse the result.
Whenever we represent a constant in a program written in some language or in data as a decimal, we do not get that particular number. We get an approximation of this number, because we work with a numerical system that cannot accurately represent decimals. And this violates the associative law.
Associative law is really important in the course of algebraic manipulation of expressions in programs. But it is not respected if the inputs / outputs and intermediate results of the calculations cannot be accurately represented.
And since none of our numbers are represented exactly, all calculations are wrong! This means that (A + B) + C is not the same as A + (B + C), and the order in which you perform the calculations can change the result.
This problem is not new. It was known when the floating-point calculations in the binary system were developed — the developers thus made a compromise.
At that time there were two schools of computation:
- those who were engaged in scientific work wrote in Fortran using floating-point numbers in the binary system;
- those who did business wrote on Cobol using binary-decimal code (binary coded decimal, BCD). The binary-decimal code allocates 4 bits for each number and conducts the usual decimal counting (using ordinary arithmetic).

Computers are getting cheaper, and now they solve almost any problems, but we are still stuck in this template with two different worlds.
Another problem in representing a floating point number in binary format is the complexity of text conversion. Take a piece of text and turn it into a number; then take a number and convert it back to a piece of text. This should be done correctly, efficiently and without surprises, using as few numbers as possible. It turns out that such a record is a very difficult problem, expensive in terms of performance.
Problem with types
In most modern programming languages there is confusion due to erroneous data types. For example, if you write in Java, each time creating a variable, property or parameter, you need to choose the right type from Bite, Char, Short, Int, Long, Float, Double. And if you choose wrong, the program may not earn. And the error does not appear immediately, and in the tests it will not be visible. It will show itself in the future when overflow occurs and the bad things associated with it.
What can happen? One of the most impressive examples was the failure of the Aryan 5. This is a rocket sent by the European Space Agency. She strongly deviated from the course, and then exploded a few seconds after the start. The reason for this was a bug in software written in Hell. Here I translated the error to Java:

They had a variable defining the horizontal offset. And she was transferred to Short, which overflowed. The result, caught in Short, was wrong. But he was sent to the guidance system and completely confused, so that the course could not be restored. This error is estimated at about half a billion dollars.
I believe that you have not yet made mistakes that would cost half a billion dollars. But could (technically it is still possible). Therefore, we should try to create recording systems and languages to avoid such problems.
DEC64
From the point of view, the choice of data type when declaring JavaScript variables is much better - this language has only one numeric type. This means that a whole class of errors can be automatically avoided. The only problem is that this type is incorrect, as these are floating point binary numbers. And we need floating-point decimal numbers, since sometimes we add up the money and we want the result to make sense.
I propose to correct this type. My correction is called DEC64, which is a modern entry for decimal floating point numbers. I recommend DEC64 as the only numerical type in future application languages. Because if you only have one numeric type, you cannot make a mistake by choosing the wrong type (I think this will provide much more value, something that we can get by having several types).
The hardware implementation of DEC64 allows you to add numbers in one cycle, which reduces the importance of performance when using the old types. The advantage of DEC64 is that in this recording, the basic operations on numbers work the way people are used to. And eliminating numeric confusion reduces errors. In addition, converting DEC64 numbers to text and vice versa is simple, efficient, and free of surprises. In fact, it is a bit more complicated than converting integers to text and back - you just need to keep track of where the decimal point is, and you can remove excess zeros from both ends, and not just from one.
DEC64 can accurately represent decimal fractions containing up to 16 digits, which is enough for most of our applications. You can represent numbers from 1 * 10 -27 to 3 with 143 zeros.
DEC64 is very similar to floating point source numbers developed in the 40s. The number is represented as two numbers that are packed into a 64-bit word. The ratio is represented by 56 bits, and the rate is 8 bits.

The reason why the exhibitor is at the end is that, in the Intel architecture, we can unpack this number almost for free. This helps in the implementation of the software.
If you want to look at the software implementation of DEC64, you can find it on GitHub . , DEC64 .
DEC64 JavaScript, . , , . DEC64 ( , JavaScript — ; - ).
= .
0/0?
- , , , — (JavaScript Undefined ). , . , - , - ( , — - ).
- , , 0 0, . , . - , .
- — null - , , . And this is reasonable.
- , . , , - . 0 , 0, ? 0?
- , 1 , N / N = 1.
- - , 2 . , — . 0/0 2. Control Data Corporation. - : «, !». « ?». « - 0 0, 2!». : «… . . , , .. , , , , . . - , - 0 0».
, 0 * n n.
, 0. , , 0, . . , , , n NaN, 0 x NaN .
?
, : , , — , - .
, . , . , , , . . , (), — 0 1, ( ). , , . 0 (, , ) .
DEC64, .
Instead of conclusion
, .

. XII , — , , . , 1202 . . , , .

, . , , 2 . , . .

— , , — true false. .

— . : -, , . . -, , , . : , .. .

, , . , , .
. — -, , , . .
, . . , . . .
? , . -, , . , . -, , . , .
— . .
, HolyJS 2017 Moscow , 10 11 .
- The Post JavaScript Apocalypse — , , JS , ES6.
- Managing Asynchronicity with RQ — , , .
Source: https://habr.com/ru/post/338832/
All Articles