Data geometry 2. Definition of di- and bi-coordinates
In the first article, a metric basis on elements is defined, - a set of vertices of a simplex or graph with known values of scalar products (Gramian) or connections (Laplacian) between them. Here we consider how to determine the coordinates of elements on such a basis.
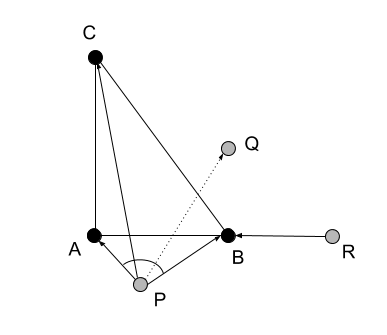
Remote coordinates are the values of scalar products of an element and reference points - the vertices of the base. We will call them di-coordinates .
The number of components of the di-coordinates is one more than the number of base vertices. l and two units more than the dimension of the basis space m = l - 1 . An example of the di-coordinates is a row (or column) of a remote metric tensor (DMT).
The remote coordinates of the element will be denoted as d m , in tensor form - subscript indicating the basis: d m a . If you need to specify which element exactly the coordinates belong to, then use brackets: d m ( P ) .
')
The complete basis includes the space normal (is a major), respectively, in the di-coordinates, you can select a scalar unit (the product of the element and the normal) and a set of scalar products of the element and the vertices of the base d :
d m = [ 1 ; d ] .
Scalar set d will also be called minor components.
We give examples of the values of the distance coordinates. Suppose there are three more points near our base triangle with known distances to the vertices of the triangle — P , Q, and R (see figure). To calculate the distances we use the Cartesian coordinates of the points on the plane ( XY ), which we present for control and verification:
The tuple of distances from point P to points A , B , C here is: [ 2 , 5 , 26 ] . Accordingly, the di-coordinates of the point will be as follows: d m ( P ) = [ 1 ; - 1.0 , - 2.5 , - 13.0 ] . For all points in space, the value of the scalar component of the di-coordinates is the same (in the framework of this series of articles).
Di-coordinates of points Q and R :
dm(Q)=[1;−6.5,−2.0,−6.5]
dm(R)=[1;−12.5,−2.0,−20.5]
The difference of elements sets the vector . In the di-coordinates of the vector, the scalar component is zero - on this basis the vector vecPQ can be distinguished from the item.
The geometry in which the description of the coordinates of points and vectors differs is called affine . In this geometry, the vector can be added to any element (point) and get a new element. For vectors, addition and subtraction operations are defined (the value of the scalar component remains zero). But usually there is no point in the operation of addition of elements.
It is easy to show that the metric tensor for distance coordinates is the Laplacian (LMT). To determine the square of the distance (distance) between the elements of P and Q, it is necessary to find the vector of the difference of elements vecpq and calculate its rate . The norm of the vector is determined through the bilinear form - the multiplication of the coordinates of the vector to the left and right and the metric tensor. For remote coordinates, this is written as:
q′(P,Q)=|| vecPQ||=dm(P−Q) Lm dm(P−Q) quad(2.1)
Where dm(P−Q)=dm(P)−dm(Q) - di-coordinates of the vector, Lm - Laplace metric tensor.
We are checking. Coordinates of the desired vector: dm(P−Q)=[1;−6.5,−2.0,−6.5]−[1;−1.0,−2.5,−13.0]=[0;−5.5,0.5,6.5] . We multiply these coordinates from two sides to the Laplace metric tensor (LMT) and get the answer: q′P,Q=13 . You can consult with the calculation of the distance through the distance in Cartesian coordinates: q(P,Q)=32+22=13 . The answers matched, the metric works.
Simplex of l vertex determines m=l−1 -dimensional space mathbbRl . The base triangle defines the base plane mathbbR2 . The number of remote components in the di-coordinates of the element is one more than the space dimensionality. This means that the di-coordinates allow you to specify elements that go beyond the base space and belong to mathbbRn . In our example, elements can lie not only in the plane of the base triangle, but also on (under) it.
The coordinates of the element do not allow to determine which side of the base space the element is located (if it is located outside). In the example with a triangle, the elements located above and below the plane of the triangle will have the same coordinates.
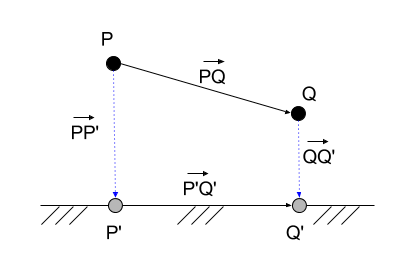
If the element does not belong to the base space, then the position of the element should be distinguished. P and its projections onto space P′ . The distance formula between elements (2.1) works only in the base space (therefore, the distance in it is marked with a dash), that is, determines the square of the distance between the projections of the elements (and not between the elements themselves):
q′(P,Q)=qa(P′,Q′) quad(2.1′)
Here through the index a marked basis, on the space of which the distance between the elements is projected. In Cartesian (and similar) coordinates there is no way to specify the coordinates of the elements beyond it. Therefore, there are no such nuances in the Cartesian coordinate system.
Opening the brackets in formula (2.1), we obtain the "cosine theorem for elements". In form, it is similar to the usual , only here we have the coordinates of the elements (and not vectors). Therefore, there are no corners or cosines. But we get the definitions of the norms of elements relative to the basis:
q(P′,Q′)=n(P)+n(Q)−2g(P,Q) quad(2.2)
n(P)=dm(P) Lm dm(P) quad(2.3)
g(P,Q)=dm(P) Lm dm(Q) quad(2.4)
Scalar n(p) will be called the norm of the element, and the scalar g(P,Q) - the scalar product of elements. Here the dot product is expressed in terms of the bilinear form.
Calculate the rate of the element P shown in the picture. Multiplying the di-coordinates of an element twice by the LMT metric tensor, we get zero: n(P)=0 . What does it mean?
The element rate characterizes its position relative to the base space, - is equal to the negative distance from the element to the space :
n(P)=−q(P,P′) quad(2.4.1) .
The value of the norm allows determining whether an element belongs to the space of a basis or not, and if not, how far it is from it.
Elements with zero norm are conveniently called points of space - these are local elements. Elements with non-zero norm are non-local with respect to a basis space.
The geometric meaning of the scalar product of vectors is well known — it reflects the cosine of the angle between their directions.
To interpret the scalar product of elements, we turn to formula (2.2), (see also the figure of the projections). Having regrouped the terms, we obtain, taking into account (2.4.1):
g(P,Q)=−(q(P′,Q′)+q(P,P′)+q(Q,Q′)/2 quad(2.5)
We see that the doubled scalar product is the sum of the distances from the elements to the base space and the distance between the projections of the elements in the base space.
Denote by g(PP′,QQ′) following combination of distances:
g(PP′,QQ′)=−(q(P,Q)+q(P′,Q′)−q(P,Q′)−q(P′,Q))/2 quad(2.5.1)
This expression is a scalar product of ordered pairs. (P,p′) and (Q,Q′) normals of elements to space. Now we can express the product of elements through the distance between them and the product of normals:
g(P,Q)=−q(P,Q)/2−g(PP′,QQ′) quad(2.6)
This formula allows you to determine the distance to the elements outside the space of the base.
If the normal scalar product is zero g(PP′,QQ′)=0 (for example, one of the elements belongs to the space of the basis), then the distance between the elements is determined by their scalar product:
q(P,Q)=−2g(P,Q) quad(2.6.1)
Formula (2.6.1) reveals the meaning of the scalar product of elements - it reflects the square of the distance between elements with a coefficient (-1/2).
If the elements are outside the base space, then in order to determine the exact distance between them, in addition to the coordinates, additional information is required - namely, the value of the scalar product of the normals to the space g(PP′,QQ′) . This scalar product can be calculated under the condition that the elements belong to the same superspace. In this case, the scalar product between the normals of elements is simply the product of their lengths. Then the “magic” formula for calculating the distance between non-local elements will be as follows:
q(P,Q)/(−2)=g(P,Q)+sign(P,Q) sqrtn(P) n(Q) quad(2.7)
Scalar value sign(P,Q) equals 1 if the elements are located on one side of the space and -1 if they are different. This formula is simply a special (but important) case of identity (2.6). In many applications, the location of elements is always one-sided, so the formula (2.7) can be used to determine the distance between objects (being, for example, in the air) if their di-coordinates are known relative to reference points (radars on the ground).
It is not easy to imagine that, for example, a 3-dimensional space also has a side, but mathematics says it does. In Cartesian coordinates, the side to which the element belongs is determined by the sign of the value of the nth component, which is not included in the baseline. If the tetrahedron is given in Cartesian coordinates x, y, z, and there is still one component (for example, t is time), then we can assume that the plane t = 0 divides the base space into two sides. Elements with a component t> 0 lie on one side of the base space, and those with t <0 on the other.
Mutual with respect to distance coordinates are the bi-coordinates of the element. The term is connected with the fact that bi-coordinates actually represent an extension of the barycentric coordinates. The metric tensor for bi-coordinates is the distance tensor.
Element bi-coordinates are denoted in superscript tensor form. bma . The transition from di-coordinates to bi-coordinates (and back) is performed by multiplying by the corresponding metric basis tensor:
bmi=Lmijdmj, quaddmi=Gmijbmj quad(2.8)
Calculate the bi-coordinates of the element P relative to the vertices of our triangle. Performing the multiplication LMT on the di-coordinates of the element, we get:
bmi=Lmijdmj=[−3/2;11/12,1/3,−1/4]
The peculiarity of the barycentric coordinates is that the sum of their components is 1 (in our example 11/12 + 1/3 - 1/4 = 1). Each barycentric component is the contribution (weight) of the vertex of the base to the coordinate of the element. The greater the value of the component, the closer the element is to the base vertex.
The structure of bi-coordinates can be written as: bm=[w;b] .
Here b - barycentric coordinates, and w - orbital element. The orbital reflects the scalar product of the element and the basic sphere Z :
w(P)=P cdotZ quad(2.9)
In geometry, there is the concept of the degree of a point m(P) - the position of a point relative to a given sphere. Set as the difference between the distance from the point to the center of the sphere q(P,O) and radius of sphere r :
m(P,O)=q(P,O)−r(O) quad(2.9.1)

The figure is the square of the length of the leg |PT| triangle POT (from point to tangency of the sphere) is equal to the value of the degree of the point P. The points M and N in the figure demonstrate the useful property of a degree, namely that its value is equal to the product of the lengths of the segments |Pm| and |Mn| .
The orbital of the element can be expressed in terms of the degree of the element relative to the sphere of the base:
w(P)=−m(P,Z′)/2=−(r(P)−rs)/2 quad(2.9.2) .
If the orbital is greater than zero, the element lies inside the sphere of the base; if it is smaller, it lies outside. Barycentric coordinates b characterize the position of the projection of the element in the space of the base simplex, and the scalar component defines the spatial position relative to the sphere.
The orbital of the basis vertices is zero (since the elements of the basis belong to the sphere). The bi-coordinates of the basis vertices are unit coordinates (with a unit in its base component and zero in the rest - usually denoted by e ). For example, the bi-coordinates of the vertex A of a triangle will be equal to [0; 100].
If the element does not belong to the space of the basis, then its distance to the center of the sphere r(P) equal to the sum of the distances from the element to its projection q(P,P′) and distances from projection to center r(P′) . The first is equal to the rate of the element with the opposite sign. Then you can express the orbital of the element through the orbital of its projection wP′ and rate n(p) :
w(P)=w(P′)−n(P)/2 quad(2.9.3)
In turn, the orbital of the projection can be determined through the bi-linear form of the barycentric coordinates of the element and the minor Gramian of the basis G :
w(P′)=−bi(P)Gijbj(P)/2 quad(2.9.4)
In the 5th part we show that the concept of the orbitals of an element relative to a sphere can be generalized to the definition of the mutual orbitals of elements. Which in turn is associated with the concept of the scalar product of vectors.
As in the case of di-coordinates, one should distinguish the bi-coordinates of an element from the bi-coordinates of the vector of the difference of elements (affine geometry). However, the criterion for distinguishing the two types of coordinates in this system is different. The sum of the barycentric components of the element is 1, and the sum of the components of the vector will be 0 (since the difference) is the balance vectors . (Balance vectors are used in accounting transactions). The rest is similar. Bi-vectors can be added and subtracted - while the result remains in the space of vectors.
The orbital (the scalar component of the bi-coordinate) of the vector reflects the magnitude of the projection of the center of the sphere of the basis on the vector. It does not depend on the norm (square of the radius) of the sphere.
The bi-coordinates of the center of the base sphere are bordered by the Laplace metric tensor. Recalling that the sum of the components of the Laplacian is zero, we can conclude that the rows (columns) of the Laplacian of the basis reflect the bi-coordinates of certain vectors. These are vectors of the dual basis ; we do not dwell on them here in detail.
The scalar component adds a metric to the barycentric coordinates. With the known metric tensor (DMT), it is possible to calculate the distances between the elements belonging to the base space. Everything is standard - through the bilinear form of multiplying the difference of coordinates by the metric tensor. Formulas are similar to expressions in di-coordinates with the replacement of the metric tensor. Lm on Gm and di coordinates dm on bi-coordinates bm . Denoting the bi-coordinates of the difference vector of elements as bm(Q−P)=bm(Q)−bm(P) we get:
Distance between projections: q′(P,Q)=bm(Q−P) Gm bm(Q−P) quad(2.10.1)
Item Rate: n(P)=bm(P) Gm bm(P) quad(2.10.2)
Scalar product: g(P,Q)=bm(P) Gm bm(Q) quad(2.10.3)
Knowing the bi-coordinates of the elements and their position relative to the base space also allows you to calculate the distance between the elements outside the base space by the formula (2.6). And that's cool. It is usually assumed that the barycentric coordinates specify only the relative position of the elements. It turns out that if we add to them a scalar component in the form of an orbital, then it is possible to determine the spatial position of not only the element itself, but also the distances between the elements outside the base space.
As already noted, the full (major) set of elements of the basis includes the space normal vector mathbfz . Di-coordinates of the normal have the form: [0; eleven,...]. Accordingly, the bi-coordinates of the normal are mutually inverse: [1; 0, 0, ...]. The di-coordinates of the normal vector are included in the structure of the remote metric tensor.
The fact that the normal is a vector is indicated by the value of zero in the scalar component of the di-coordinates and the equality to zero of the sum of the barycentric coordinates.
The normal norm (the convolution of the di- and bi-coordinates) is always zero, since the projection of the normal to any space will always be a point.
As a consequence, the space normal can be added to the elements. Such an operation changes the norm of the element, but not its position in space. Knowing the coordinates of the projection element P′ and rate n(p) , you can always determine the coordinates of the element itself P . To do this, multiply the normal vector by the element's seminorm and add the resulting vector to the projection coordinates.
P=P′+n(P)/2 mathbfz quad(2.11)
If in the relationship formula of di- and bi-coordinates (2.8) to reveal the structure of multiplying matrices and vectors, then we can obtain useful identities for the scalar and minor components of the coordinates. For bi-coordinates we have:
Lm \ space dm = bm \ space \ Rightarrow \ space \ begin {pmatrix} rs & s ^ j \\ s ^ i & L ^ {ij} \ end {pmatrix} \ begin {pmatrix} 1 \\ d_j \ end {pmatrix} = \ begin {pmatrix} rs + s ^ j d_j \\ s ^ i + L ^ {ij} d_j \ end {pmatrix} = \ begin {pmatrix} w \\ b ^ i \ end {pmatrix} \ quad (2.12)
Here dj,bi - minor di- and bi-coordinates of elements. In this way:
Lijdj=bi−si quad(2.12.1)
sidi=w−rs quad(2.12.2)
Expression (2.12.1) demonstrates that the result of the action of the Laplacian on a vector can be interpreted as the vector of the difference between the element and the center of the sphere.
The identity (2.12.2) (in the derivation also used (2.9) and (2.10)) shows how, knowing the minor component of the di-coordinates, to get its degree and distance to the center of the sphere.
Let us turn to the structure of di-coordinates:
Gm \ space bm = dm \ space \ Rightarrow \ space \ begin {pmatrix} 0 & 1_j \\ 1_i & G_ {ij} \ end {pmatrix} \ begin {pmatrix} w \\ b ^ i \ end {pmatrix} = \ begin {pmatrix} 1_j b ^ j \\ w 1_i + G_ {ij} b ^ j \ end {pmatrix} = \ begin {pmatrix} 1 \\ d_i \ end {pmatrix} \ quad (2.13)
From
1 j b j = 1 q u a d ( 2.13.1 )
d i = w 1 i + G i j b j q u a d ( 2.13.2 )
The first identity shows that the sum of the barycentric components is equal to 1, and this was already known (but this shows why - because we use the unit vector as the border of the distance matrix).
The second shows the role of the orbitals in remote coordinates. Distance vector d i consists of the weight sum of the distance vectors of the vertices of the base G i j b j and the normal vector to the base space, the value of which is given by the orbital of the element. If the element lies on the sphere of the basis, then no additional bias towards the normal is required.
Using the scalar product of the coordinates of both types (bi- and di-), you can get rid of the metric tensors in the formulas.
Distance between projections: q′(P,Q)=bmi(Q−P) dmi(Q−P) quad(2.14.1)
Item Rate: n(P)=dmi(P) bmi(P) quad(2.14.2)
Scalar product: g ( P , Q ) = d m i ( P ) b m i ( Q ) = d m i ( Q ) b m i ( P ) q u a d ( 2.14.3 )
Let us briefly list the main definitions.
d m i - the di-coordinates of the element, the set of scalar products of the element and the basis frames,
b m i - the bi-coordinates of the element, the coefficients of the linear decomposition of the element in terms of basis points,Changing the type of coordinates (from di- to bi- and back) (“juggling indices”) is performed by multiplying by the corresponding metric tensor
b m i = d m j L m i j , d m i = b m j G m i j Scalar product of elements:
g = d m i L m i j d m j = b m i G m i j b m j = b m i d m i
→ P Q =Q-Pis a vector, the difference of the elements, theNorm of the difference vector is the distance between the projections of the elements on the basis space:
q ( P ′ , Q ′ ) = n ( → P Q ) = b m i ( Q - P ) d m i ( Q - P )( 2.17.3 )
___
In the next article, we consider the scalar product of ordered pairs.
Table of contents
1. Simplexes and graphs
2. Definition of di- and bi-coordinates
3. Scalar product pairs
4. The space of the graph
5. Base conversion
6. Count star
2. Definition of di- and bi-coordinates
3. Scalar product pairs
4. The space of the graph
5. Base conversion
6. Count star

Remote coordinates
Remote coordinates are the values of scalar products of an element and reference points - the vertices of the base. We will call them di-coordinates .
The number of components of the di-coordinates is one more than the number of base vertices. l and two units more than the dimension of the basis space m = l - 1 . An example of the di-coordinates is a row (or column) of a remote metric tensor (DMT).
The remote coordinates of the element will be denoted as d m , in tensor form - subscript indicating the basis: d m a . If you need to specify which element exactly the coordinates belong to, then use brackets: d m ( P ) .
')
The complete basis includes the space normal (is a major), respectively, in the di-coordinates, you can select a scalar unit (the product of the element and the normal) and a set of scalar products of the element and the vertices of the base d :
d m = [ 1 ; d ] .
Scalar set d will also be called minor components.
We give examples of the values of the distance coordinates. Suppose there are three more points near our base triangle with known distances to the vertices of the triangle — P , Q, and R (see figure). To calculate the distances we use the Cartesian coordinates of the points on the plane ( XY ), which we present for control and verification:
Matrix of Cartesian coordinates of points:
\ begin {array} {c | cccccc}
XY & A & B & C & P & Q & R \\
\ hline
X & 0 & 3 & 0 & 1 & 3 & 5 \\
Y & 0 & 0 & 4 & -1 & 2 & 0 \\
\ end {array}
XY & A & B & C & P & Q & R \\
\ hline
X & 0 & 3 & 0 & 1 & 3 & 5 \\
Y & 0 & 0 & 4 & -1 & 2 & 0 \\
\ end {array}
The tuple of distances from point P to points A , B , C here is: [ 2 , 5 , 26 ] . Accordingly, the di-coordinates of the point will be as follows: d m ( P ) = [ 1 ; - 1.0 , - 2.5 , - 13.0 ] . For all points in space, the value of the scalar component of the di-coordinates is the same (in the framework of this series of articles).
Di-coordinates of points Q and R :
dm(Q)=[1;−6.5,−2.0,−6.5]
dm(R)=[1;−12.5,−2.0,−20.5]
Elements and Vectors
The difference of elements sets the vector . In the di-coordinates of the vector, the scalar component is zero - on this basis the vector vecPQ can be distinguished from the item.
The geometry in which the description of the coordinates of points and vectors differs is called affine . In this geometry, the vector can be added to any element (point) and get a new element. For vectors, addition and subtraction operations are defined (the value of the scalar component remains zero). But usually there is no point in the operation of addition of elements.
The term <vector> is overloaded.
In the world of (linear) algebra, usually vector space is understood as a certain linear space in which elements are characterized by a set of numbers, and addition and subtraction operations are defined.
In such a space there is no difference between elements and vectors - “all vector”.
In our space it is not.
In such a space there is no difference between elements and vectors - “all vector”.
In our space it is not.
Distance between elements
It is easy to show that the metric tensor for distance coordinates is the Laplacian (LMT). To determine the square of the distance (distance) between the elements of P and Q, it is necessary to find the vector of the difference of elements vecpq and calculate its rate . The norm of the vector is determined through the bilinear form - the multiplication of the coordinates of the vector to the left and right and the metric tensor. For remote coordinates, this is written as:
q′(P,Q)=|| vecPQ||=dm(P−Q) Lm dm(P−Q) quad(2.1)
Where dm(P−Q)=dm(P)−dm(Q) - di-coordinates of the vector, Lm - Laplace metric tensor.
We are checking. Coordinates of the desired vector: dm(P−Q)=[1;−6.5,−2.0,−6.5]−[1;−1.0,−2.5,−13.0]=[0;−5.5,0.5,6.5] . We multiply these coordinates from two sides to the Laplace metric tensor (LMT) and get the answer: q′P,Q=13 . You can consult with the calculation of the distance through the distance in Cartesian coordinates: q(P,Q)=32+22=13 . The answers matched, the metric works.
To check the calculations, we give the value of our base LMT from the previous article.
\ begin {array} {c | cccc}
Lm (A, B, C) & * & A & B & C \\
\ hline
* & 6.25 & 0 & 0.5 & 0.5 \\
A & 0 & 25/144 & -16/144 & -9/144 \\
B & 0.5 & -16/144 & 16/144 & 0 \\
C & 0.5 & -9/144 & 0 & 9/144 \\
\ end {array}
Lm (A, B, C) & * & A & B & C \\
\ hline
* & 6.25 & 0 & 0.5 & 0.5 \\
A & 0 & 25/144 & -16/144 & -9/144 \\
B & 0.5 & -16/144 & 16/144 & 0 \\
C & 0.5 & -9/144 & 0 & 9/144 \\
\ end {array}
Element and its projection on the base space
Simplex of l vertex determines m=l−1 -dimensional space mathbbRl . The base triangle defines the base plane mathbbR2 . The number of remote components in the di-coordinates of the element is one more than the space dimensionality. This means that the di-coordinates allow you to specify elements that go beyond the base space and belong to mathbbRn . In our example, elements can lie not only in the plane of the base triangle, but also on (under) it.
The coordinates of the element do not allow to determine which side of the base space the element is located (if it is located outside). In the example with a triangle, the elements located above and below the plane of the triangle will have the same coordinates.

If the element does not belong to the base space, then the position of the element should be distinguished. P and its projections onto space P′ . The distance formula between elements (2.1) works only in the base space (therefore, the distance in it is marked with a dash), that is, determines the square of the distance between the projections of the elements (and not between the elements themselves):
q′(P,Q)=qa(P′,Q′) quad(2.1′)
Here through the index a marked basis, on the space of which the distance between the elements is projected. In Cartesian (and similar) coordinates there is no way to specify the coordinates of the elements beyond it. Therefore, there are no such nuances in the Cartesian coordinate system.
The element rate and distance to the base space
Opening the brackets in formula (2.1), we obtain the "cosine theorem for elements". In form, it is similar to the usual , only here we have the coordinates of the elements (and not vectors). Therefore, there are no corners or cosines. But we get the definitions of the norms of elements relative to the basis:
q(P′,Q′)=n(P)+n(Q)−2g(P,Q) quad(2.2)
n(P)=dm(P) Lm dm(P) quad(2.3)
g(P,Q)=dm(P) Lm dm(Q) quad(2.4)
Scalar n(p) will be called the norm of the element, and the scalar g(P,Q) - the scalar product of elements. Here the dot product is expressed in terms of the bilinear form.
Calculate the rate of the element P shown in the picture. Multiplying the di-coordinates of an element twice by the LMT metric tensor, we get zero: n(P)=0 . What does it mean?
The element rate characterizes its position relative to the base space, - is equal to the negative distance from the element to the space :
n(P)=−q(P,P′) quad(2.4.1) .
The value of the norm allows determining whether an element belongs to the space of a basis or not, and if not, how far it is from it.
Elements with zero norm are conveniently called points of space - these are local elements. Elements with non-zero norm are non-local with respect to a basis space.
Scalar product of elements
The geometric meaning of the scalar product of vectors is well known — it reflects the cosine of the angle between their directions.
To interpret the scalar product of elements, we turn to formula (2.2), (see also the figure of the projections). Having regrouped the terms, we obtain, taking into account (2.4.1):
g(P,Q)=−(q(P′,Q′)+q(P,P′)+q(Q,Q′)/2 quad(2.5)
We see that the doubled scalar product is the sum of the distances from the elements to the base space and the distance between the projections of the elements in the base space.
Denote by g(PP′,QQ′) following combination of distances:
g(PP′,QQ′)=−(q(P,Q)+q(P′,Q′)−q(P,Q′)−q(P′,Q))/2 quad(2.5.1)
This expression is a scalar product of ordered pairs. (P,p′) and (Q,Q′) normals of elements to space. Now we can express the product of elements through the distance between them and the product of normals:
g(P,Q)=−q(P,Q)/2−g(PP′,QQ′) quad(2.6)
This formula allows you to determine the distance to the elements outside the space of the base.
If the normal scalar product is zero g(PP′,QQ′)=0 (for example, one of the elements belongs to the space of the basis), then the distance between the elements is determined by their scalar product:
q(P,Q)=−2g(P,Q) quad(2.6.1)
Formula (2.6.1) reveals the meaning of the scalar product of elements - it reflects the square of the distance between elements with a coefficient (-1/2).
Distance between elements outside the base space
If the elements are outside the base space, then in order to determine the exact distance between them, in addition to the coordinates, additional information is required - namely, the value of the scalar product of the normals to the space g(PP′,QQ′) . This scalar product can be calculated under the condition that the elements belong to the same superspace. In this case, the scalar product between the normals of elements is simply the product of their lengths. Then the “magic” formula for calculating the distance between non-local elements will be as follows:
q(P,Q)/(−2)=g(P,Q)+sign(P,Q) sqrtn(P) n(Q) quad(2.7)
Scalar value sign(P,Q) equals 1 if the elements are located on one side of the space and -1 if they are different. This formula is simply a special (but important) case of identity (2.6). In many applications, the location of elements is always one-sided, so the formula (2.7) can be used to determine the distance between objects (being, for example, in the air) if their di-coordinates are known relative to reference points (radars on the ground).
It is not easy to imagine that, for example, a 3-dimensional space also has a side, but mathematics says it does. In Cartesian coordinates, the side to which the element belongs is determined by the sign of the value of the nth component, which is not included in the baseline. If the tetrahedron is given in Cartesian coordinates x, y, z, and there is still one component (for example, t is time), then we can assume that the plane t = 0 divides the base space into two sides. Elements with a component t> 0 lie on one side of the base space, and those with t <0 on the other.
Bi-coordinates
Mutual with respect to distance coordinates are the bi-coordinates of the element. The term is connected with the fact that bi-coordinates actually represent an extension of the barycentric coordinates. The metric tensor for bi-coordinates is the distance tensor.
Element bi-coordinates are denoted in superscript tensor form. bma . The transition from di-coordinates to bi-coordinates (and back) is performed by multiplying by the corresponding metric basis tensor:
bmi=Lmijdmj, quaddmi=Gmijbmj quad(2.8)
Calculate the bi-coordinates of the element P relative to the vertices of our triangle. Performing the multiplication LMT on the di-coordinates of the element, we get:
bmi=Lmijdmj=[−3/2;11/12,1/3,−1/4]
The peculiarity of the barycentric coordinates is that the sum of their components is 1 (in our example 11/12 + 1/3 - 1/4 = 1). Each barycentric component is the contribution (weight) of the vertex of the base to the coordinate of the element. The greater the value of the component, the closer the element is to the base vertex.
Element orbital
The structure of bi-coordinates can be written as: bm=[w;b] .
Here b - barycentric coordinates, and w - orbital element. The orbital reflects the scalar product of the element and the basic sphere Z :
w(P)=P cdotZ quad(2.9)
In geometry, there is the concept of the degree of a point m(P) - the position of a point relative to a given sphere. Set as the difference between the distance from the point to the center of the sphere q(P,O) and radius of sphere r :
m(P,O)=q(P,O)−r(O) quad(2.9.1)

The figure is the square of the length of the leg |PT| triangle POT (from point to tangency of the sphere) is equal to the value of the degree of the point P. The points M and N in the figure demonstrate the useful property of a degree, namely that its value is equal to the product of the lengths of the segments |Pm| and |Mn| .
The orbital of the element can be expressed in terms of the degree of the element relative to the sphere of the base:
w(P)=−m(P,Z′)/2=−(r(P)−rs)/2 quad(2.9.2) .
If the orbital is greater than zero, the element lies inside the sphere of the base; if it is smaller, it lies outside. Barycentric coordinates b characterize the position of the projection of the element in the space of the base simplex, and the scalar component defines the spatial position relative to the sphere.
The orbital of the basis vertices is zero (since the elements of the basis belong to the sphere). The bi-coordinates of the basis vertices are unit coordinates (with a unit in its base component and zero in the rest - usually denoted by e ). For example, the bi-coordinates of the vertex A of a triangle will be equal to [0; 100].
If the element does not belong to the space of the basis, then its distance to the center of the sphere r(P) equal to the sum of the distances from the element to its projection q(P,P′) and distances from projection to center r(P′) . The first is equal to the rate of the element with the opposite sign. Then you can express the orbital of the element through the orbital of its projection wP′ and rate n(p) :
w(P)=w(P′)−n(P)/2 quad(2.9.3)
In turn, the orbital of the projection can be determined through the bi-linear form of the barycentric coordinates of the element and the minor Gramian of the basis G :
w(P′)=−bi(P)Gijbj(P)/2 quad(2.9.4)
In the 5th part we show that the concept of the orbitals of an element relative to a sphere can be generalized to the definition of the mutual orbitals of elements. Which in turn is associated with the concept of the scalar product of vectors.
Bi-coordinates of elements and vectors
As in the case of di-coordinates, one should distinguish the bi-coordinates of an element from the bi-coordinates of the vector of the difference of elements (affine geometry). However, the criterion for distinguishing the two types of coordinates in this system is different. The sum of the barycentric components of the element is 1, and the sum of the components of the vector will be 0 (since the difference) is the balance vectors . (Balance vectors are used in accounting transactions). The rest is similar. Bi-vectors can be added and subtracted - while the result remains in the space of vectors.
The orbital (the scalar component of the bi-coordinate) of the vector reflects the magnitude of the projection of the center of the sphere of the basis on the vector. It does not depend on the norm (square of the radius) of the sphere.
The bi-coordinates of the center of the base sphere are bordered by the Laplace metric tensor. Recalling that the sum of the components of the Laplacian is zero, we can conclude that the rows (columns) of the Laplacian of the basis reflect the bi-coordinates of certain vectors. These are vectors of the dual basis ; we do not dwell on them here in detail.
Distance and norms in bi-coordinates
The scalar component adds a metric to the barycentric coordinates. With the known metric tensor (DMT), it is possible to calculate the distances between the elements belonging to the base space. Everything is standard - through the bilinear form of multiplying the difference of coordinates by the metric tensor. Formulas are similar to expressions in di-coordinates with the replacement of the metric tensor. Lm on Gm and di coordinates dm on bi-coordinates bm . Denoting the bi-coordinates of the difference vector of elements as bm(Q−P)=bm(Q)−bm(P) we get:
Distance between projections: q′(P,Q)=bm(Q−P) Gm bm(Q−P) quad(2.10.1)
Item Rate: n(P)=bm(P) Gm bm(P) quad(2.10.2)
Scalar product: g(P,Q)=bm(P) Gm bm(Q) quad(2.10.3)
Knowing the bi-coordinates of the elements and their position relative to the base space also allows you to calculate the distance between the elements outside the base space by the formula (2.6). And that's cool. It is usually assumed that the barycentric coordinates specify only the relative position of the elements. It turns out that if we add to them a scalar component in the form of an orbital, then it is possible to determine the spatial position of not only the element itself, but also the distances between the elements outside the base space.
Combine di and bi-coordinates
Normal to space - a special vector
As already noted, the full (major) set of elements of the basis includes the space normal vector mathbfz . Di-coordinates of the normal have the form: [0; eleven,...]. Accordingly, the bi-coordinates of the normal are mutually inverse: [1; 0, 0, ...]. The di-coordinates of the normal vector are included in the structure of the remote metric tensor.
The fact that the normal is a vector is indicated by the value of zero in the scalar component of the di-coordinates and the equality to zero of the sum of the barycentric coordinates.
The normal norm (the convolution of the di- and bi-coordinates) is always zero, since the projection of the normal to any space will always be a point.
As a consequence, the space normal can be added to the elements. Such an operation changes the norm of the element, but not its position in space. Knowing the coordinates of the projection element P′ and rate n(p) , you can always determine the coordinates of the element itself P . To do this, multiply the normal vector by the element's seminorm and add the resulting vector to the projection coordinates.
P=P′+n(P)/2 mathbfz quad(2.11)
Connection of parameters of the basis with the coordinates of elements
If in the relationship formula of di- and bi-coordinates (2.8) to reveal the structure of multiplying matrices and vectors, then we can obtain useful identities for the scalar and minor components of the coordinates. For bi-coordinates we have:
Lm \ space dm = bm \ space \ Rightarrow \ space \ begin {pmatrix} rs & s ^ j \\ s ^ i & L ^ {ij} \ end {pmatrix} \ begin {pmatrix} 1 \\ d_j \ end {pmatrix} = \ begin {pmatrix} rs + s ^ j d_j \\ s ^ i + L ^ {ij} d_j \ end {pmatrix} = \ begin {pmatrix} w \\ b ^ i \ end {pmatrix} \ quad (2.12)
Here dj,bi - minor di- and bi-coordinates of elements. In this way:
Lijdj=bi−si quad(2.12.1)
sidi=w−rs quad(2.12.2)
Expression (2.12.1) demonstrates that the result of the action of the Laplacian on a vector can be interpreted as the vector of the difference between the element and the center of the sphere.
The identity (2.12.2) (in the derivation also used (2.9) and (2.10)) shows how, knowing the minor component of the di-coordinates, to get its degree and distance to the center of the sphere.
Let us turn to the structure of di-coordinates:
Gm \ space bm = dm \ space \ Rightarrow \ space \ begin {pmatrix} 0 & 1_j \\ 1_i & G_ {ij} \ end {pmatrix} \ begin {pmatrix} w \\ b ^ i \ end {pmatrix} = \ begin {pmatrix} 1_j b ^ j \\ w 1_i + G_ {ij} b ^ j \ end {pmatrix} = \ begin {pmatrix} 1 \\ d_i \ end {pmatrix} \ quad (2.13)
From
1 j b j = 1 q u a d ( 2.13.1 )
d i = w 1 i + G i j b j q u a d ( 2.13.2 )
The first identity shows that the sum of the barycentric components is equal to 1, and this was already known (but this shows why - because we use the unit vector as the border of the distance matrix).
The second shows the role of the orbitals in remote coordinates. Distance vector d i consists of the weight sum of the distance vectors of the vertices of the base G i j b j and the normal vector to the base space, the value of which is given by the orbital of the element. If the element lies on the sphere of the basis, then no additional bias towards the normal is required.
Norms are a convolution of coordinates of different types.
Using the scalar product of the coordinates of both types (bi- and di-), you can get rid of the metric tensors in the formulas.
Distance between projections: q′(P,Q)=bmi(Q−P) dmi(Q−P) quad(2.14.1)
Item Rate: n(P)=dmi(P) bmi(P) quad(2.14.2)
Scalar product: g ( P , Q ) = d m i ( P ) b m i ( Q ) = d m i ( Q ) b m i ( P ) q u a d ( 2.14.3 )
Putting it all together
Let us briefly list the main definitions.
d m i - the di-coordinates of the element, the set of scalar products of the element and the basis frames,
b m i - the bi-coordinates of the element, the coefficients of the linear decomposition of the element in terms of basis points,Changing the type of coordinates (from di- to bi- and back) (“juggling indices”) is performed by multiplying by the corresponding metric tensor
b m i = d m j L m i j , d m i = b m j G m i j Scalar product of elements:
g = d m i L m i j d m j = b m i G m i j b m j = b m i d m i
→ P Q =Q-Pis a vector, the difference of the elements, theNorm of the difference vector is the distance between the projections of the elements on the basis space:
q ( P ′ , Q ′ ) = n ( → P Q ) = b m i ( Q - P ) d m i ( Q - P )( 2.17.3 )
___
In the next article, we consider the scalar product of ordered pairs.
Source: https://habr.com/ru/post/338290/
All Articles