Padding Oracle Attack: cryptography still scares

This vulnerability has been repaired for fifteen years.

The four-year-old text “Padding Oracle Attack or why cryptography scares” described the CBC encryption mode in detail. In this mode, each regular plaintext block xor-is with the previous ciphertext block: as a result, each ciphertext block depends on each plaintext block that has been processed by that moment.

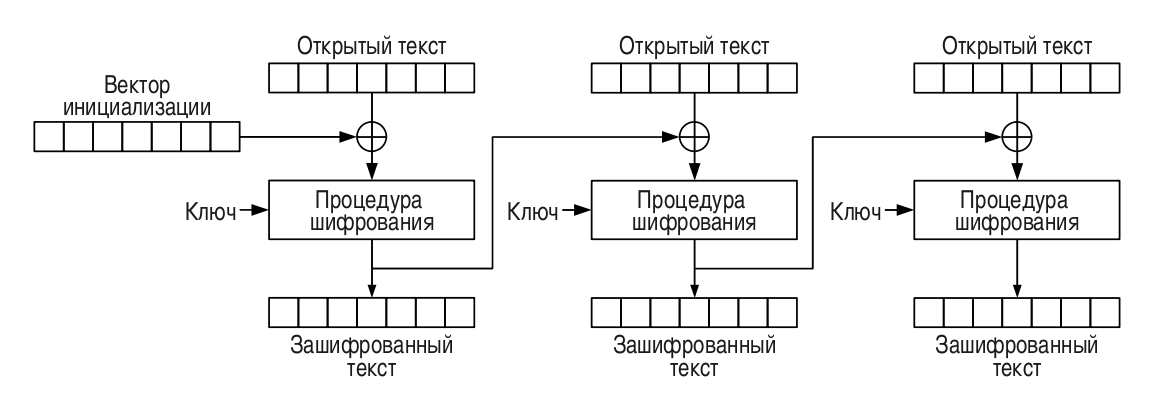
To skip the original message (of arbitrary length) through the CBC cipher, it is appended with a MAC (hash for integrity checking, usually 20-byte SHA-1) and then padding to complete the plaintext to an integer number of blocks (usually 16-byte):


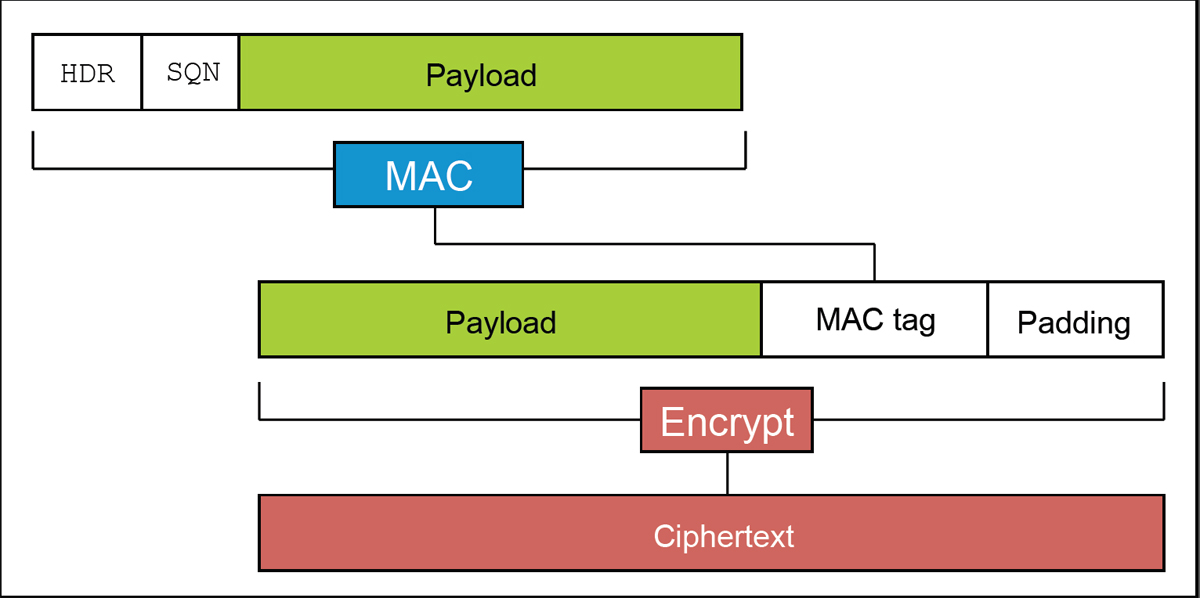
Padding consists of equal bytes, one less than its length: (0) or (1,1) or (2,2,2) or the like.
Thus, the recipient of the ciphertext should

1. decipher all its blocks;
2. read the last byte of the last block to determine the length of the padding and, accordingly, the MAC position in clear text;
3. check the correctness of the packing and MAC.

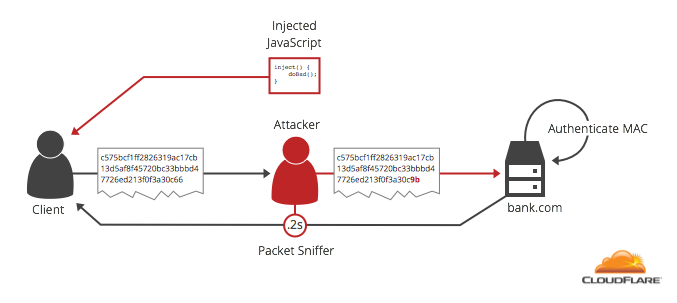
In 2002, French cryptographer Serge Vodenet discovered a vulnerability to padding oracle attacks in CBC: if you intercept a ciphertext (using a MitM attack), change the last byte of the penultimate block, send the modified ciphertext to the server, and monitor its response, then the difference between the “incorrect packing” and “incorrect MAC” answers will make it possible to determine the last byte in 256 requests source plaintext. Then MitM begins to change the penultimate byte of the penultimate block, and for 256 requests it determines the penultimate byte of plaintext, etc. - 256 requests to decrypt each byte.

Practically, this vulnerability could (was) be used to steal an HTTPS cookie: the attacker sends the user to his page, on which the script, on behalf of the user, will send HTTPS requests to the server of interest to the attacker one by one. The user's browser will insert his cookies for this server into each request, while the MitM server, controlled by the attacker, will intercept messages between the user and the HTTPS server, change one byte in them in the penultimate block, and monitor the server's response. It will take less than a minute to decrypt all cookies.

It would seem that to protect against Vodene’s attack, it is enough that the server returns the same error code if the code is incorrect and the MAC is incorrect; but these two cases can still be distinguished in time until the server responds: calculating and checking the MAC takes significantly more time than just checking the stuffing in the last block.
')
Since there should be no difference, packing or MAC did not pass the check - it may seem that there is no need to check the contents of the packing: if the plaintext does not end with a sequence of identical bytes, then it is obviously incorrect, so the MAC will not coincide with the overwhelming probability. But if an attacker selects such a ciphertext size so that the last block is completely occupied with stuffing and replaces it with any previous block from the same ciphertext on the MitM server, the server will report an error only if the last byte of the substituted block is not decrypted in (block_length – 1). It turns out the same "padding oracle", only in profile. This attack was called POODLE . Modern SSL / TLS implementations necessarily check the contents of the stuffing, and if it is incorrect, they consider the stuffing to be absent, and send the entire CBC decryption result to the MAC check. In principle, this allows customers not to send an extra block, consisting entirely of stuffing, when the plaintext (along with the MAC) initially consists of an integer number of blocks, and does not end with a sequence of identical bytes.

After these corrections, the padding oracle vulnerabilities were considered eliminated until, in 2013, a pair of British researchers invented the Lucky 13 attack, which is based on the fact that the MAC calculation time depends on the length of the hashed string. Since SHA-1 processes a string with 64-byte blocks, an attacker can try all possible two-byte combinations as the last two bytes of the penultimate CBC block, and a jump in server response time will mean a transition between a 55-byte hash string (one SHA-1 block ; a nine-byte "trailer") and a 56-byte (two blocks) are added to the end of the hashed string, i.e. between two byte packing and single byte:


By intercepting and changing the HTTPS request 65,536 times, measuring the response time of the server each time, the last two bytes of plaintext can be restored in a “sterile” laboratory environment. In practice, the accumulation of sufficient statistics to restore two bytes will require more than one hundred repetitions of this series of 65536 queries. Thus, the attack "Lucky 13" was more likely a theoretical danger.

This attack got its name due to the fact that the size of the header, which is hashed before the “payload”, limited the search for packing options to double-byte sequences. Whether this header is 14-byte or longer, a jump in the server response time would fall on shorter pieces of plaintext, and it would take hundreds of times more stuffing options to sort through. On the other hand, if this header were 11-byte, the jump would fall on the transition between blocks 8 and 9 of plaintext, and the attack would be completely impossible. Well, the happiest number is, of course, 12: with such a header length, it would be enough for an attack to iterate over the values ​​of the last byte in itself, as in the Vodene attack.

To protect against “Lucky 13”, the OpenSSL developers have put forth a remarkable ingenuity : in fact, it is impossible to use branching in the entire MAC verification code and the packing, otherwise the verification time for different input data will be different! Omitting the details of the implementation of the SHA-1 without branching by the number of blocks processed, let us focus on the last verification step: comparing the calculated MAC value with the actual recorded in clear text. To avoid branching, the code checks the entire plaintext byte by byte, combining the difference between the expected and actual values ​​with the “MAC mask” and the “packing mask”, and combining the results of all bytes with OR:


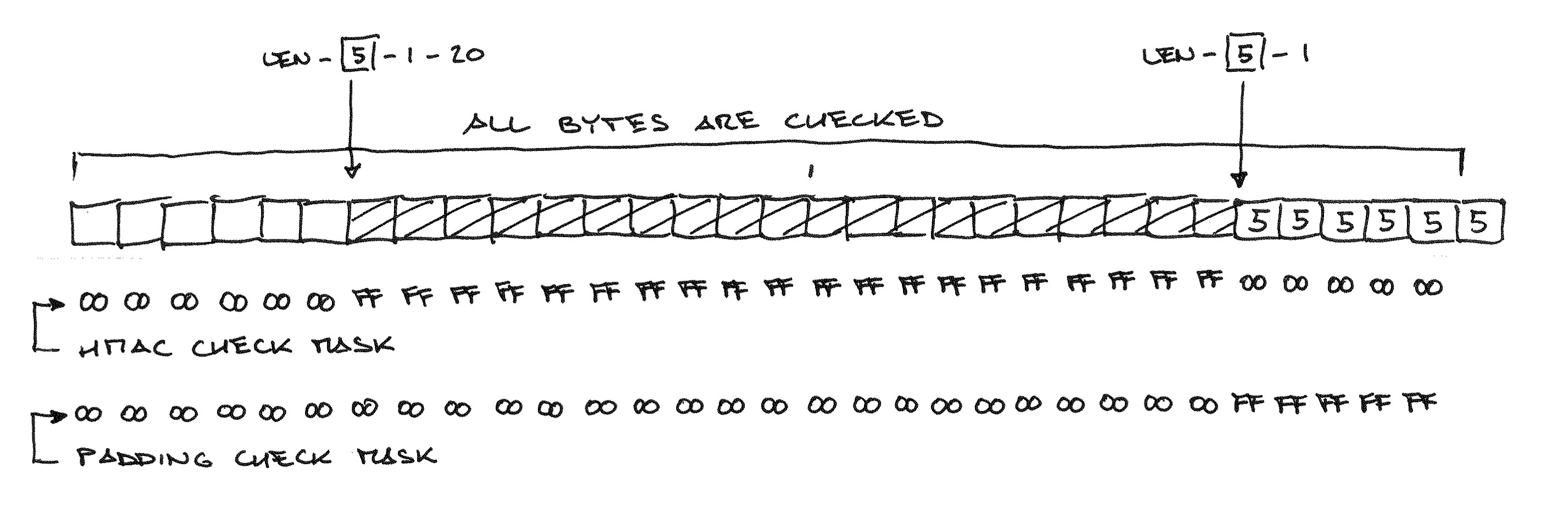
The 32-byte plaintext depicted consists of a six-byte message, 20 MAC bytes, and six stuffing bytes. Packing can be no longer than 12 bytes (with an empty message), but in any case, the code must calculate the MAC and check all the bytes of the message before returning an error code.

Well, what will this code do if the last byte of the plaintext is "12" - a deliberately impossible packing length?

The MAC will be calculated for a message of length -1!
No matter how the result will turn out, it is obviously meaningless; more importantly, the MAC check mask “moved” by one byte per start of the message — i.e. from the resulting garbage value only 19 bytes will be checked.

But what if you move the MAC mask entirely behind the beginning of the message?


Now you can ignore the MAC check: anyway, all difference bytes will be pro-and-yens with a zero mask! The only remaining obstacle is checking the contents of the pack. All its bytes must be equal to the last, i.e. 31:

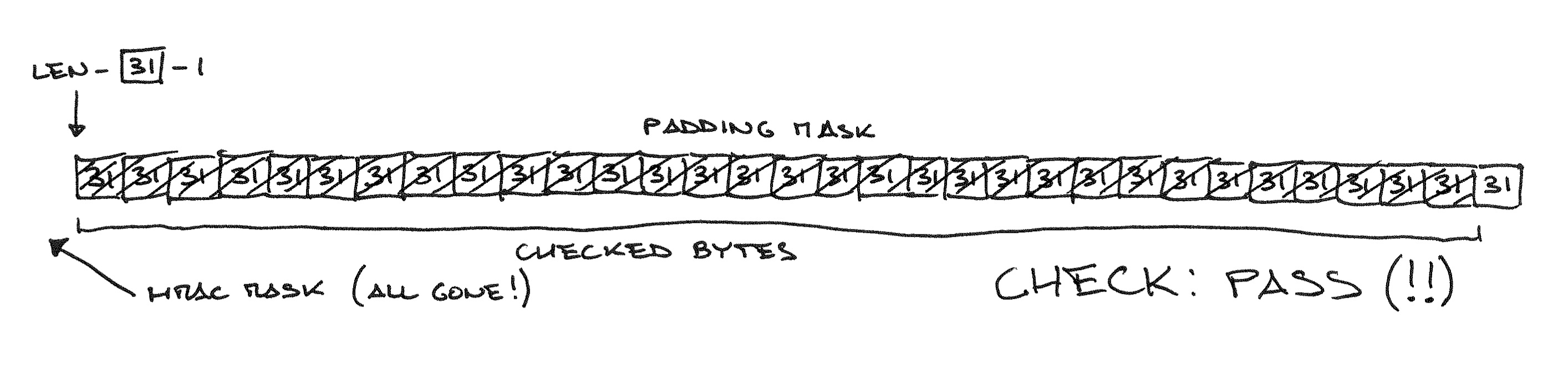
Thus, the attacker can check whether the plaintext will consist entirely of bytes with a value (cryptographic length – 1): in this case, OpenSSL will consider the ciphertext correct, and the server will return a higher level error (for example, an HTTP error).

How to use such an oracle? Now the MitM server has to act much more sophisticated than when attacking Vodene. Suppose an attacker script sent a POST request to the HTTPS server ending in 31 bytes with a value of 31. The MitM server intercepts the ciphertext, takes only the last two blocks from it, and as the initialization vector takes the third end of the ciphertext and will it with each request to change the first byte:


Of the 256 attempts with different values ​​of the first byte IV, 255 will lead to the error "incorrect MAC or stuffing", and one attempt will lead to another error - so we can recover the 32nd byte from the end of the POST request!
In the POST request, we increase the length of the path by one byte, and shorten the request body by byte, then we will know the 31st from the end of the request. Now we change the second byte IV so that the second byte of plaintext again turns 31. Again we will change the first byte IV, and again we can restore the 32nd byte from the end of the query!
Shifting the “transparent byte” in this way, MitM can decrypt the last 16 bytes in the POST header, and, if lucky, the HTTPS cookies will be among the 16 bytes. The decryption rate is the same as in the original Vodenet attack: up to 256 requests for each recovered byte. It turns out that incidentally with the protection of "Lucky 13" in OpenSSL introduced a vulnerability that is much more serious than the very "Lucky 13"!

Technical Note: even if the POST request ends in a sequence of bytes 31, it will be supplemented by MAC and stuffing before CBC encryption, so that in the described form the attack will not work. Preparatory stage of the attack - by varying the requested path, choose a POST request length so that the MAC and this padding occupy the last two CBC blocks in their entirety; then during the attack these last two blocks will be discarded, and blocks from the fifth to the third from the end will be used. By establishing such coordination between the script that generates HTTPS requests and the MitM server, an attacker can ensure that the result of the CBC decryption will end in 31 bytes with a value of 31.

Summing up: over the course of 15 years since the discovery of the first “padding oracle”, each attempt to eliminate such “oracles” was followed by the discovery (or even inadvertent creation!) Of new ones. I wonder how much time will pass until the next “padding oracle” is found in TLS using CBC ciphers?