Learn OpenGL. Lesson 2.5 - Light Sources

Sources of light

Up to this article, we were content with lighting coming from one point in space. And the result was not bad, but in reality there are many sources of illumination with differing "behavior". This lesson discusses several such light sources. The ability to simulate the characteristics of different light sources is another tool to enrich the created scenes.

We begin the lesson with a directional light source, then move on to a point source, which is a development of the above simple lighting method. In the end we will look at how the source is imitating the properties of a spotlight (spotlight).

Directional light source

If the light source is significantly removed from the object of observation, then the incoming rays of light are practically parallel to each other, giving the impression that the light is directed equally regardless of the location of the object and / or observer. A simulated infinitely distant light source is called a directional, since all its rays are considered to go in one direction and do not depend on the location of the source itself.
A good example of this type of source is our sun. Suppose it is not infinitely distant from us, but this distance is enough to consider it infinitely remote in the calculations of illumination. And assume that the rays of sunlight are parallel, as shown in the figure:


Since we consider the rays parallel, the mutual arrangement of the illuminated object and the source is not important - the direction of the rays will be the same throughout the scene. Accordingly, the calculation of lighting will be the same for all objects, since the direction vector of the lighting is the same for any object in the scene.

To model a directional source, we can specify the direction vector of the light, and the position vector is no longer needed. The model of calculations in the shader remains almost unchanged: the calculation of the source direction vector lightDir using the source position vector is replaced by the direct use of the specified direction vector direction .

struct Light { // vec3 position; //    . vec3 direction; vec3 ambient; vec3 diffuse; vec3 specular; }; ... void main() { vec3 lightDir = normalize(-light.direction); ... } 

Notice the inverse of the light.direction vector. Until now, the computation model accepted the direction vector of the light source as oriented from the fragment to the source , but for directional sources the direction vector is usually set as oriented from the source . Therefore, an inversion is performed, and in a variable we save the vector directed to the light source. Also do not forget about the normalization - it is better not to hope that the input data will be normalized.

So, as a result, lightDir is used in the calculations of the diffuse and specular component in the same way as before.

In order to demonstrate that the directional source equally affects the illumination of many objects, we will use the familiar scene code with a crowd of containers from the final of the Coordinate Systems lesson. For those who missed: first we set 10 different positions of containers and set each of them on a unique model matrix that stores the corresponding transformations from the local coordinate system to the world:

 for(unsigned int i = 0; i < 10; i++) { glm::mat4 model(1.); model = glm::translate(model, cubePositions[i]); float angle = 20.0f * i; model = glm::rotate(model, glm::radians(angle), glm::vec3(1.0f, 0.3f, 0.5f)); lightingShader.setMat4("model", model); glDrawArrays(GL_TRIANGLES, 0, 36); } 

Also, do not forget to pass the direction of our directional source to the shader (once again I remind you that we set the direction from the source; by the form of the vector you can determine that it is directed downwards):

 lightingShader.setVec3("light.direction", -0.2f, -1.0f, -0.3f); 

So far, we have transmitted the positions and directions as three-component vectors ( vec3 ), however some developers prefer transmission in the form of vectors with four components ( vec4 ). When specifying positions with the help of vec4, it is extremely important to set the component w to 1 so that the transfer and projection transformations are correctly applied. At the same time, when specifying directions in the form of vec4, we would not want the transfer to affect the direction (this is the direction vector, after all), and therefore we must set w = 0 .

Thus, the direction vector is represented as vec4 (0.2f, 1.0f, 0.3f, 0.0f) . Such a record can also be used for an affordable check on the type of light source and the choice of the lighting calculation model: if the component w is 1, then this is clearly the position vector of the light source, if w is 0, then we have the direction vector:

 if(lightVector.w == 0.0) //      //       else if(lightVector.w == 1.0) //        // (   ) 

Fun fact: this is how OpenGL defined the light source as directional or positioned and changed the calculation model during the fixed-pipeline times (fixed-functionality).

If we now assemble our application, then moving around the scene, we can see that all objects are illuminated by a source that is similar to the sun in its behavior. See how the diffuse and specular component of illumination on objects changes as if a source of light is located somewhere in the conventional sky? The results should be something like this:


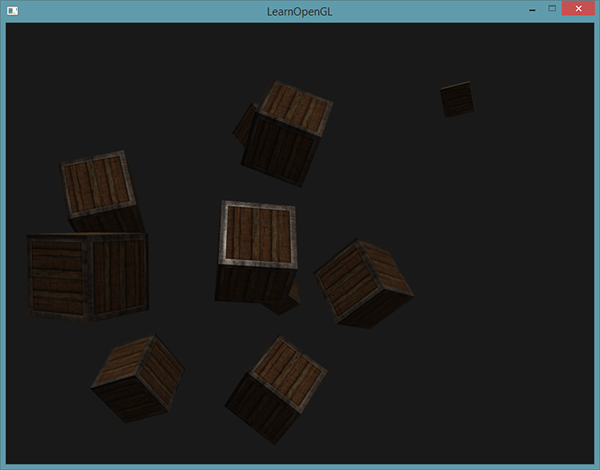
The source code of the sample can be found here .

Point sources

Directional light sources do a good job with lighting the entire scene, but usually we need to place a few more point sources in the scene space. A point light source has a predetermined position in space and radiates uniformly in all directions, and the illumination intensity decreases with distance. Conventional incandescent lamps or torches can be cited as an example of point sources.


In previous lessons we used the simplest implementation of a point source with a given position, which spreads light in all directions. However, the rays of this source did not fade with removal, which made the source look extremely powerful. In most scenes created, it would be desirable to have sources that affect the environment in close proximity to them, but not to the whole scene at once.

If you add 10 containers to the scene of the previous example, you will notice that even the most distant ones are lit with the same intensity as those directly in front of the source. And this is expected - we did not take into account any expressions that control the intensity of illumination. But we want the removed containers to be only slightly highlighted compared to those closest to the source.

Attenuation

Attenuation of light intensity with distance is called attenuation. The simplest method for calculating attenuation is using a linear law. In this case, the intensity will linearly decrease with distance, providing less illumination of distant objects. But visually this model gives unrealistic results. In the general case, real light sources give strong illumination in the vicinity, but the intensity rather sharply decreases in a small radius and then its remaining stock slowly decreases with distance. To imitate such behavior, a calculation is needed that is sharper than linear.
Fortunately, physicists are not asleep, and the generalized expression for calculating the attenuation coefficient from distance has long been derived. It remains only to calculate the value for each fragment and multiply the intensity vector of a specific source by the result:

$$

$${{F} _ {att}} = \ frac {1.0} {{{K} _ {c}} + {{K} _ {l}} d + {{K} _ {q}} {{d} ^ {2}}}$$

where $$$d$ - the distance from the fragment to the source, $$${K} _ {c}, {K} _ {l}, {K} _ {q}$ - constant, linear and quadratic coefficients.

• The constant coefficient is, as usual, equal to 1.0, performing protection against reducing the value of the denominator to values ​​less than unity, which would lead to an increase in the illumination intensity at certain distances. For us, this effect is undesirable.
• The linear coefficient determines the term that linearly reduces the intensity of light with increasing distance.
• The quadratic coefficient determines the term defining the quadratic intensity decrease. At small distances, the contribution of the quadratic term will be covered by the linear contribution, but with increasing distance it will become dominant in the expression.

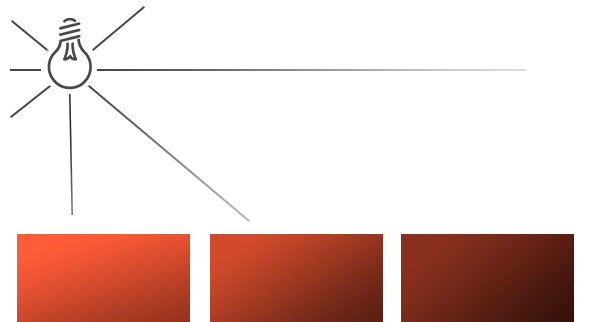
The combination of linear and quadratic dependence allows you to create an effect when the intensity decreases linearly near the source, and after a certain removal line begins to subside much faster. As a result, the brightness of the source is high near, decreases rather rapidly with increasing distance, and at large distances decreases more slowly. The following graph shows an example of the attenuation coefficient over 100 units of distance:


As can be seen, the intensity is greatest at small distances, but with growth it decreases significantly and tends to zero in the vicinity of 100 units.

Selection of coefficients

There is a question of choosing three factors. $$${K} _ {c}, {K} _ {l}, {K} _ {q}$ . Suitable values ​​are searched based on the environment being developed in the scene, the required lighting distance, type of source, and other factors. In most cases, this becomes a matter of experience and a certain amount of adjustment by trial and error. The table below contains a list of parameters that provide a realistic, in a certain sense, behavior of a light source covering a specified distance. The first column indicates the distance of coverage at fixed coefficients. The table is taken from the wiki page of the Ogre3D engine and is an excellent starting point for selecting the values ​​you need.

Distance	Constant	Linear	Quadratic
7	1.0	0.7	1.8
13	1.0	0.35	0.44
20	1.0	0.22	0.20
32	1.0	0.14	0.07
50	1.0	0.09	0.032
65	1.0	0.07	0.017
100	1.0	0.045	0.0075
160	1.0	0.027	0.0028
200	1.0	0.022	0.0019
325	1.0	0.014	0.0007
600	1.0	0.007	0.0002
3250	1.0	0.0014	0.000007

As you can see, the constant coefficient is everywhere equal to one. The linear coefficient is chosen small when illuminating large distances, and the quadratic coefficient is even smaller. Try experimenting with these values ​​and personally see what effect their change has on your implementation. For the scenes in question, the coverage distance is from 32 to 100 units. quite enough.

Implementation

To implement the attenuation, we need three additional parameters in the fragment shader code: the actual, constant, linear, and quadratic coefficients. It is most logical to store them as part of the declared Light structure that we used earlier. Note that the calculation of the lightDir vector is carried out similarly to the previous lesson, and not by the method described in the directional light source section.

 struct Light { vec3 position; vec3 ambient; vec3 diffuse; vec3 specular; float constant; float linear; float quadratic; }; 

Next, set the specific values ​​of the parameters in the code. We will need a lighting distance of about 50 units, for which the following values ​​are given in the table:

 lightingShader.setFloat("light.constant", 1.0f); lightingShader.setFloat("light.linear", 0.09f); lightingShader.setFloat("light.quadratic", 0.032f); 

The calculation code in the fragment shader is obvious: we calculate the attenuation coefficient and then multiply the background, diffuse and specular lighting components by it.

For calculations, however, we need the value of the distance from the fragment to the light source. How do we get it? It's simple: just calculate the difference of the position vector of the fragment and the source, and use the built-in GLSL function length () :

 float distance = length(light.position - FragPos); float attenuation = 1.0 / (light.constant + light.linear * distance + light.quadratic * (distance * distance)); 

As a result, we multiply the coefficient obtained by all the components of the lighting model.

It would be possible to leave the background component without fading, however, in scenes with several sources, the contribution of this component will begin to add up, which is usually undesirable. In this case, attenuation is also included for the background component.

 ambient *= attenuation; diffuse *= attenuation; specular *= attenuation; 

By running the test application, you can expect something like this:



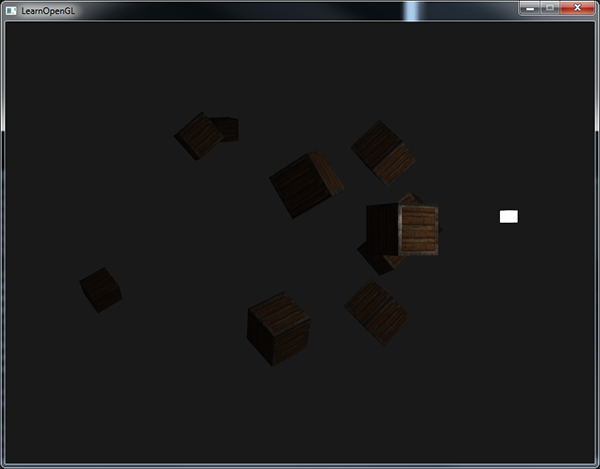
It can be seen that now only the containers in front are highlighted, and the closest one is the brightest. The containers in the back of the stage are not illuminated at all, because they are too far from the source.

Full sample code can be found here . Summing up, we can say that the point source we call a source with adjustable position and taking into account the attenuation of the intensity in the calculations of illumination. Another tool in our piggy bank!

Spotlight

The last considered source type will be a spotlight. Such a source has a predetermined position, but radiates not in all directions, but only in the selected one. At the same time, objects are illuminated only in a small neighborhood from a given direction, while objects lying outside this area remain without illumination. As an example, imagine a street lamp or a hand torch.

In our model, the searchlight will be represented by the position in world coordinates, the direction vector and the cut-off angle , which determines the radius of illumination of the searchlight. To determine whether a fragment is highlighted or not, we will calculate whether it is inside or outside the cone-shaped source cut-off zone. This scheme will help to figure out how everything works:


Here LightDir is the vector directed from the fragment to the source, SpotDir is the vector of the direction of the searchlight, $$$\ phi$ ( phi ) - clipping angle that determines the radius of the backlight (fragments outside this angle will not be highlighted) $$$\ theta$ ( theta ) - the angle between the LightDir and SpotDir vectors (if $$$\ theta$ less than $$$\ phi$ , the fragment falls into the backlight zone).

Thus, all that needs to be done is to calculate the scalar product of the vectors LightDir and SpotDir and compare the value obtained with the specified cut-off angle (with the cosine of the angle, because scalar multiplication returns the cosine of the angle between two normalized vectors). Now that you have a basic understanding of the device of the searchlight, you can proceed to the implementation.

Implementation

Let's bring the model to life in the form of a flashlight, i.e. source recorded at the position of the observer and directed straight ahead from his point of view. In fact, a flashlight is a source of the type of searchlight, with a position and direction rigidly attached to the position and orientation of the player.

To transfer to the shader, we need the position values ​​(to calculate the vector to the light source), the direction vector of the spotlight and the clipping angle. All this can be put into the Light structure:

 struct Light { vec3 position; vec3 direction; float cutOff; ... }; 

Next, we transfer the data to the shader in the program code:

 lightingShader.setVec3("light.position", camera.Position); lightingShader.setVec3("light.direction", camera.Front); lightingShader.setFloat("light.cutOff", glm::cos(glm::radians(12.5f))); 

As you can see, here we are not transmitting the cut-off angle, but its cosine, since in the shader we calculate the scalar product of vectors, which returns the cosine of the angle between them. In order to avoid calculating the cosine angle with the call to the expensive acos () function, we will pass the finished cosine of the cut-off angle to the shader and compare these values ​​directly, saving some computational resources.

Actually, we will calculate and determine whether we are inside the zone of the searchlight or not:

 float theta = dot(lightDir, normalize(-light.direction)); if(theta > light.cutOff) { //   } //     ,     //      else color = vec4(light.ambient * vec3(texture(material.diffuse, TexCoords)), 1.0); 

First, we compute the scalar product of the vectors of LightDir and the inverted vector of direction (since we need a vector directed to the source, not from it). Do not forget to normalize all used vectors!

You may be surprised at the use of the comparison sign “>” instead of “<” in the conditional operator. It seems theta must be less than the cut-off value so that the fragment is in the cone of the action of the searchlight? That's right, but we are not comparing the corners here, but their cosines. The cosine of 0 ° is 1, and 90 ° is 0. Look at the graph:

Obviously, the cosine value tends to 1 as the angle decreases, which explains why theta should be greater than the cut-off value. In this example, the cutoff value is equal to the cosine of an angle of 12.5 °, which is equal to 0.9978. Accordingly, the fragment will be in the backlight cone, if the theta value is in the range from 0.9978 to 1.0.

The launch of the test application will show that now only those fragments are highlighted that lie inside the searchlight cone:


The complete example code is here .

The results, however, are not impressive. The hard, sharp edges of the highlighted area look especially unrealistic. Fragments that have fallen from the spotlight cone are shaded instantly, without a decrease in brightness. It is realistic to smoothly reduce the illumination intensity in the cut-off zone.

Smooth attenuation

To implement a spotlight with soft edges of the backlight zone, we will need to specify the inner and outer cones of this zone. The inner cone can be determined based on the data discussed in the previous section. From its borders to the borders of the outer cone, the intensity should fade out smoothly.

The outer cone is determined by the cosine of the angle of the solution of this cone. As a result, for a fragment that is in the gap between the boundaries of two cones, the illumination intensity between 0.0 and 1.0 should be calculated. Fragments lying in the inner cone are always illuminated with an intensity of 1.0, and those outside the outer cone are not illuminated at all.

You can calculate the parameter that determines the smooth decrease in intensity using the following formula:

$$

$$I = \ frac {\ theta - \ gamma} {\ varepsilon}$$

where $$$\ varepsilon = \ phi - \ gamma$ - the difference of cosines of the angles defining the internal ( $$$\ phi$ ) and external ( $$$\ gamma$ ) cones, $$$I$ - coefficient of the intensity of illumination for this fragment.

Practically, it can be difficult to imagine how a given expression behaves, so consider a couple of examples:

θ	Θ °	ϕ (internal)	ϕ °	γ (external)	γ °	ε	I
0.87	thirty	0.91	25	0.82	35	0.91 - 0.82 = 0.09	0.87 - 0.82 / 0.09 = 0.56
0.9	26	0.91	25	0.82	35	0.91 - 0.82 = 0.09	0.9 - 0.82 / 0.09 = 0.89
0.97	14	0.91	25	0.82	35	0.91 - 0.82 = 0.09	0.97 - 0.82 / 0.09 = 1.67
0.83	34	0.91	25	0.82	35	0.91 - 0.82 = 0.09	0.83 - 0.82 / 0.09 = 0.11
0.64	50	0.91	25	0.82	35	0.91 - 0.82 = 0.09	0.64 - 0.82 / 0.09 = -2.0
0.966	15	0.9978	12.5	0.953	17.5	0.966 - 0.953 = 0.0448	0.966 - 0.953 / 0.0448 = 0.29

As you can see, this is a simple interpolation operation between the cosine of the external and internal cut-off angle depending on the value $$$\ theta$ . If now it is not clear what is happening, then do not worry - you can simply take the formula as a given and return to it after a year as an experienced and sophisticated person.

One problem - value $$$I$ now it turns out to be less than zero in the region outside the outer cone, greater than one in the region of the inner cone and intermediate values ​​between the boundaries. It is necessary to correctly limit the range of values ​​in order to eliminate the need for conditional operators and simply multiply the components of the lighting model by the calculated intensity value:

 float theta = dot(lightDir, normalize(-light.direction)); float epsilon = light.cutOff - light.outerCutOff; float intensity = clamp((theta - light.outerCutOff) / epsilon, 0.0, 1.0); ... // we'll leave ambient unaffected so we always have a little light. diffuse *= intensity; specular *= intensity; ... 

Pay attention to the function clamp () , which limits the range of values ​​of its first parameter to the values ​​of the second and third parameters. In this case, the intensity value will lie on the segment [0, 1].

Do not forget to add the outerCutOff parameter to the Light structure and configure the transfer of a specific value to the uniform variable of the shader. For this image, the inside angle is set at 12.5 °, and the outside angle is 17.5 °:


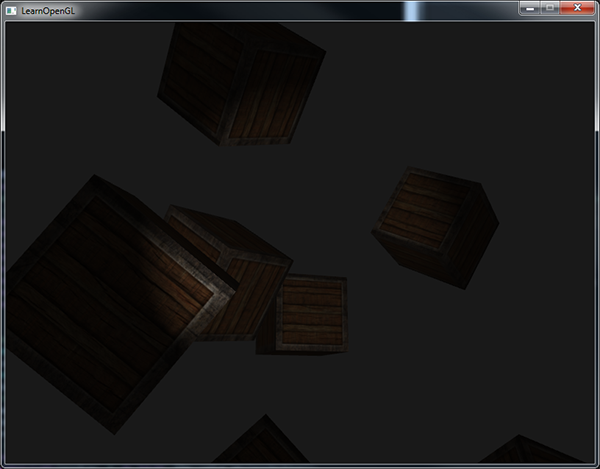
Much better! Now you can play with the settings of the clipping zones and get a spotlight that is perfect for your task. The source code of the application can be found here .

This type of flashlight source is ideal for horror games, and in combination with directional and point sources, the scenes you create will be radically transformed.

In the next lesson, we will try to use all the types of sources and graphic techniques that are currently considered.

Tasks

Try experimenting with all the types of sources described and their fragment shaders. Invert some vectors and / or change the comparison signs. Understand for yourself the results of such actions.

Original article .