Balanced B-tree Search Tree (t = 2)
Introduction and formulation of the problem
In the 3rd year of study at my university, I was faced with the task of implementing a B-tree containing unique keys, ordered in ascending order (with degree t = 2) in c ++ (with the ability to add, delete, search for elements and, accordingly, rebuild the tree) .
Having re-read several articles on Habré (for example, B-tree , 2-3-tree. Naive implementation and others), it would seem, everything was clear. Only theoretically, not practically. But I managed to cope with these difficulties. The purpose of my post is to share my experience with users.
Few highlights
A b-tree is a tree that satisfies the following properties:
1. Each node contains at least one key. The root contains from 1 to 2t-1 keys. Any other node contains from t-1 to 2t-1 keys. Leaves are no exception to this rule. Here t is a tree parameter, not less than 2.
2. The leaves have no descendants. Any other node containing n keys contains n + 1 descendants. Wherein:
a) The first descendant and all its descendants contain keys from the interval
b) For
c) (n + 1) -th descendant and all its descendants contain keys from the interval
3. The depth of all leaves is the same.
Implementation
To begin, create a node structure of our tree.
Node structure
const int t=2; struct BNode { int keys[2*t]; BNode *children[2*t+1]; BNode *parent; int count; // int countSons; // bool leaf; }; Now create a class Tree, which includes the appropriate methods.
')
Class tree
class Tree { private: BNode *root; void insert_to_node(int key, BNode *node); void sort(BNode *node); void restruct(BNode *node); void deletenode(BNode *node); bool searchKey(int key, BNode *node); void remove(int key, BNode *node); void removeFromNode(int key, BNode *node); void removeLeaf(int key, BNode *node); void lconnect(BNode *node, BNode *othernode); void rconnect(BNode *node, BNode *othernode); void repair(BNode *node); public: Tree(); ~Tree(); void insert(int key); bool search(int key); void remove(int key); }; Immediately describe the constructor and destructor. The destructor calls the recursive method of removing elements from the tree.
Constructor and destructor
Tree::Tree() { root=nullptr; } Tree::~Tree(){ if(root!=nullptr) deletenode(root); } void Tree::deletenode(BNode *node){ if (node!=nullptr){ for (int i=0; i<=(2*t-1); i++){ if (node->children[i]!=nullptr) deletenode(node->children[i]); else { delete(node); break; } } } } First of all, consider adding a key to a node. In my case (t = 2) it will look like this:
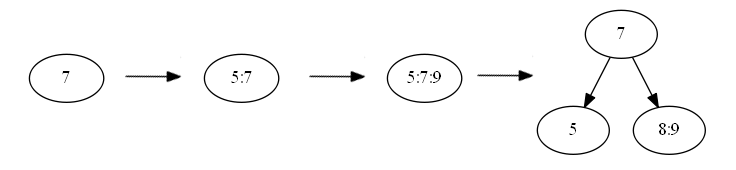
That is, as soon as there are more than 3 elements in a node, the node is broken.
So, to add an element to the tree, you must implement several methods.
The first is a simple addition to the node. In this method, the sorting method is called, which is necessary to fulfill the condition about increasing values of the tree. The second method is
adding a value to the node in which the desired position is preliminarily searched and
of necessity (in the node becomes more than 3 elements) the third method is called - the method of splitting the node into: parent and two sons.
The first method is the simple add method.
Simple add method
void Tree::insert_to_node(int key, BNode *node){ node->keys[node->count]=key; node->count=node->count+1; sort(node); } The method of sorting numbers in the node:
Sorting method
void Tree::sort(BNode *node) { int m; for (int i=0; i<(2*t-1); i++){ for (int j=i+1; j<=(2*t-1); j++){ if ((node->keys[i]!=0) && (node->keys[j]!=0)){ if ((node->keys[i]) > (node->keys[j])){ m=node->keys[i]; node->keys[i]=node->keys[j]; node->keys[j]=m; } } else break; } } } I think everything is clear.
The second method is a method of adding a value to a node with a preliminary position search:
The method of adding to the node with a preliminary search
void Tree::insert(int key){ if (root==nullptr) { BNode *newRoot = new BNode; newRoot->keys[0]=key; for(int j=1; j<=(2*t-1); j++) newRoot->keys[j]=0; for (int i=0; i<=(2*t); i++) newRoot->children[i]=nullptr; newRoot->count=1; newRoot->countSons=0; newRoot->leaf=true; newRoot->parent=nullptr; root=newRoot; } else { BNode *ptr=root; while (ptr->leaf==false){ // , for (int i=0; i<=(2*t-1); i++){ // if (ptr->keys[i]!=0) { if (key<ptr->keys[i]) { ptr=ptr->children[i]; break; } if ((ptr->keys[i+1]==0)&&(key>ptr->keys[i])) { ptr=ptr->children[i+1]; // , "" break; } } else break; } } insert_to_node(key, ptr); while (ptr->count==2*t){ if (ptr==root){ restruct(ptr); break; } else { restruct(ptr); ptr=ptr->parent; } } } } The third method is the node splitting method :
Node splitting method
void Tree::restruct(BNode *node){ if (node->count<(2*t-1)) return; // BNode *child1 = new BNode; int j; for (j=0; j<=t-2; j++) child1->keys[j]=node->keys[j]; for (j=t-1; j<=(2*t-1); j++) child1->keys[j]=0; child1->count=t-1; // if(node->countSons!=0){ for (int i=0; i<=(t-1); i++){ child1->children[i]=node->children[i]; child1->children[i]->parent=child1; } for (int i=t; i<=(2*t); i++) child1->children[i]=nullptr; child1->leaf=false; child1->countSons=t-1; // } else { child1->leaf=true; child1->countSons=0; for (int i=0; i<=(2*t); i++) child1->children[i]=nullptr; } // BNode *child2 = new BNode; for (int j=0; j<=(t-1); j++) child2->keys[j]=node->keys[j+t]; for (j=t; j<=(2*t-1); j++) child2->keys[j]=0; child2->count=t; // if(node->countSons!=0) { for (int i=0; i<=(t); i++){ child2->children[i]=node->children[i+t]; child2->children[i]->parent=child2; } for (int i=t+1; i<=(2*t); i++) child2->children[i]=nullptr; child2->leaf=false; child2->countSons=t; // } else { child2->leaf=true; child2->countSons=0; for (int i=0; i<=(2*t); i++) child2->children[i]=nullptr; } // if (node->parent==nullptr){ // , node->keys[0]=node->keys[t-1]; for(int j=1; j<=(2*t-1); j++) node->keys[j]=0; node->children[0]=child1; node->children[1]=child2; for(int i=2; i<=(2*t); i++) node->children[i]=nullptr; node->parent=nullptr; node->leaf=false; node->count=1; node->countSons=2; child1->parent=node; child2->parent=node; } else { insert_to_node(node->keys[t-1], node->parent); for (int i=0; i<=(2*t); i++){ if (node->parent->children[i]==node) node->parent->children[i]=nullptr; } for (int i=0; i<=(2*t); i++){ if (node->parent->children[i]==nullptr) { for (int j=(2*t); j>(i+1); j--) node->parent->children[j]=node->parent->children[j-1]; node->parent->children[i+1]=child2; node->parent->children[i]=child1; break; } } child1->parent=node->parent; child2->parent=node->parent; node->parent->leaf=false; delete node; } } The following methods were implemented for the search , returning true or false (the second method is recursive):
Search
bool Tree::search(int key){ return searchKey(key, this->root); } bool Tree::searchKey(int key, BNode *node){ if (node!=nullptr){ if (node->leaf==false){ int i; for (i=0; i<=(2*t-1); i++){ if (node->keys[i]!=0) { if(key==node->keys[i]) return true; if ((key<node->keys[i])){ return searchKey(key, node->children[i]); break; } } else break; } return searchKey(key, node->children[i]); } else { for(int j=0; j<=(2*t-1); j++) if (key==node->keys[j]) return true; return false; } } else return false; } The implementation of the method of removing a key from a node was the most difficult. Indeed, in some cases, deletions need to glue adjacent nodes, and in some take values from the nodes of the "brothers". For example:
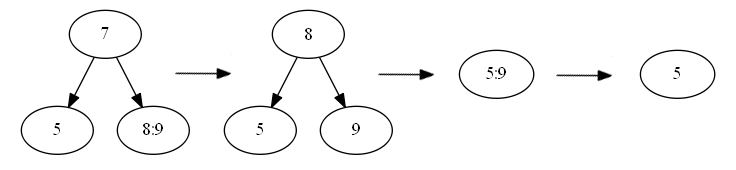
Removal is a few cases. The first one is a simple method of removing a key from a node:
Method of deleting a key from a node
void Tree::removeFromNode(int key, BNode *node){ for (int i=0; i<node->count; i++){ if (node->keys[i]==key){ for (int j=i; j<node->count; j++) { node->keys[j]=node->keys[j+1]; node->children[j]=node->children[j+1]; } node->keys[node->count-1]=0; node->children[node->count-1]=node->children[node->count]; node->children[node->count]=nullptr; break; } } node->count--; } In the second case, after removing the key, it is necessary to connect the neighboring nodes. Therefore, the second and third methods are methods of connecting nodes :
Methods of connecting nodes
void Tree::lconnect(BNode *node, BNode *othernode){ if (node==nullptr) return; for (int i=0; i<=(othernode->count-1); i++){ node->keys[node->count]=othernode->keys[i]; node->children[node->count]=othernode->children[i]; node->count=node->count+1; } node->children[node->count]=othernode->children[othernode->count]; for (int j=0; j<=node->count; j++){ if (node->children[j]==nullptr) break; node->children[j]->parent=node; } delete othernode; } void Tree::rconnect(BNode *node, BNode *othernode){ if (node==nullptr) return; for (int i=0; i<=(othernode->count-1); i++){ node->keys[node->count]=othernode->keys[i]; node->children[node->count+1]=othernode->children[i+1]; node->count=node->count+1; } for (int j=0; j<=node->count; j++){ if (node->children[j]==nullptr) break; node->children[j]->parent=node; } delete othernode; } The fourth method is the node repair method . In this method, the tree is literally rebuilt until all the conditions of the B-tree are satisfied:
Method of "repair" node
void Tree::repair(BNode *node){ if ((node==root)&&(node->count==0)){ if (root->children[0]!=nullptr){ root->children[0]->parent=nullptr; root=root->children[0]; } else { delete root; } return; } BNode *ptr=node; int k1; int k2; int positionSon; BNode *parent=ptr->parent; for (int j=0; j<=parent->count; j++){ if (parent->children[j]==ptr){ positionSon=j; // break; } } // ptr- ( ) if (positionSon==0){ insert_to_node(parent->keys[positionSon], ptr); lconnect(ptr, parent->children[positionSon+1]); parent->children[positionSon+1]=ptr; parent->children[positionSon]=nullptr; removeFromNode(parent->keys[positionSon], parent); if(ptr->count==2*t){ while (ptr->count==2*t){ if (ptr==root){ restruct(ptr); break; } else { restruct(ptr); ptr=ptr->parent; } } } else if (parent->count<=(t-2)) repair(parent); } else { // ptr- ( ) if (positionSon==parent->count){ insert_to_node(parent->keys[positionSon-1], parent->children[positionSon-1]); lconnect(parent->children[positionSon-1], ptr); parent->children[positionSon]=parent->children[positionSon-1]; parent->children[positionSon-1]=nullptr; removeFromNode(parent->keys[positionSon-1], parent); BNode *temp=parent->children[positionSon]; if(ptr->count==2*t){ while (temp->count==2*t){ if (temp==root){ restruct(temp); break; } else { restruct(temp); temp=temp->parent; } } } else if (parent->count<=(t-2)) repair(parent); } else { // ptr insert_to_node(parent->keys[positionSon], ptr); lconnect(ptr, parent->children[positionSon+1]); parent->children[positionSon+1]=ptr; parent->children[positionSon]=nullptr; removeFromNode(parent->keys[positionSon], parent); if(ptr->count==2*t){ while (ptr->count==2*t){ if (ptr==root){ restruct(ptr); break; } else { restruct(ptr); ptr=ptr->parent; } } } else if (parent->count<=(t-2)) repair(parent); } } } The fifth method is the method of removing a key from a sheet :
The method of removing the key from the sheet
void Tree::removeLeaf(int key, BNode *node){ if ((node==root)&&(node->count==1)){ removeFromNode(key, node); root->children[0]=nullptr; delete root; root=nullptr; return; } if (node==root) { removeFromNode(key, node); return; } if (node->count>(t-1)) { removeFromNode(key, node); return; } BNode *ptr=node; int k1; int k2; int position; int positionSon; int i; for (int i=0; i<=node->count-1; i++){ if (key==node->keys[i]) { position=i; // break; } } BNode *parent=ptr->parent; for (int j=0; j<=parent->count; j++){ if (parent->children[j]==ptr){ positionSon=j; // break; } } // ptr- ( ) if (positionSon==0){ if (parent->children[positionSon+1]->count>(t-1)){ // , t-1 k1=parent->children[positionSon+1]->keys[0]; //k1 - k2=parent->keys[positionSon]; //k2 - , , , , k1 insert_to_node(k2, ptr); removeFromNode(key, ptr); parent->keys[positionSon]=k1; // k1 k2 removeFromNode(k1, parent->children[positionSon+1]); // k1 } else { // <u></u> t-1 removeFromNode(key, ptr); if (ptr->count<=(t-2)) repair(ptr); } } else { // ptr- ( ) if (positionSon==parent->count){ // , t-1 if (parent->children[positionSon-1]->count>(t-1)){ BNode *temp=parent->children[positionSon-1]; k1=temp->keys[temp->count-1]; //k1 - k2=parent->keys[positionSon-1]; //k2 - , , , k1 insert_to_node(k2, ptr); removeFromNode(key, ptr); parent->keys[positionSon-1]=k1; removeFromNode(k1, temp); } else { // <u></u> t-1 removeFromNode(key, ptr); if (ptr->count<=(t-2)) repair(ptr); } } else { // ptr // , t-1 if (parent->children[positionSon+1]->count>(t-1)){ k1=parent->children[positionSon+1]->keys[0]; //k1 - k2=parent->keys[positionSon]; //k2 - , , , k1 insert_to_node(k2, ptr); removeFromNode(key, ptr); parent->keys[positionSon]=k1; // k1 k2 removeFromNode(k1, parent->children[positionSon+1]); // k1 } else { // , t-1 if (parent->children[positionSon-1]->count>(t-1)){ BNode *temp=parent->children[positionSon-1]; k1=temp->keys[temp->count-1]; //k1 - k2=parent->keys[positionSon-1]; //k2 - , , , k1 insert_to_node(k2, ptr); removeFromNode(key, ptr); parent->keys[positionSon-1]=k1; removeFromNode(k1, temp); } else { // t-1 removeFromNode(key, ptr); if (ptr->count<=(t-2)) repair(ptr); } } } } } The sixth method is the method of deletion from an arbitrary node :
Method to remove from an arbitrary node
void Tree::remove(int key, BNode *node){ BNode *ptr=node; int position; // int i; for (int i=0; i<=node->count-1; i++){ if (key==node->keys[i]) { position=i; break; } } int positionSon; // if (ptr->parent!=nullptr){ for(int i=0; i<=ptr->parent->count; i++){ if (ptr->children[i]==ptr){ positionSon==i; break; } } } // ptr=ptr->children[position+1]; int newkey=ptr->keys[0]; while (ptr->leaf==false) ptr=ptr->children[0]; // 1 - // - key , if (ptr->count>(t-1)) { newkey=ptr->keys[0]; removeFromNode(newkey, ptr); node->keys[position]=newkey; } else { ptr=node; // ptr=ptr->children[position]; newkey=ptr->keys[ptr->count-1]; while (ptr->leaf==false) ptr=ptr->children[ptr->count]; newkey=ptr->keys[ptr->count-1]; node->keys[position]=newkey; if (ptr->count>(t-1)) removeFromNode(newkey, ptr); else { // , t-1 - removeLeaf(newkey, ptr); } } } And the seventh method - the deletion method itself, which accepts as input data the value of the key to be removed from the tree.
Main removal method
void Tree::remove(int key){ BNode *ptr=this->root; int position; int positionSon; int i; if (searchKey(key, ptr)==false) { return; } else { // , for (i=0; i<=ptr->count-1; i++){ if (ptr->keys[i]!=0) { if(key==ptr->keys[i]) { position=i; break; } else { if ((key<ptr->keys[i])){ ptr=ptr->children[i]; positionSon=i; i=-1; } else { if (i==(ptr->count-1)) { ptr=ptr->children[i+1]; positionSon=i+1; i=-1; } } } } else break; } } if (ptr->leaf==true) { if (ptr->count>(t-1)) removeFromNode(key,ptr); else removeLeaf(key, ptr); } else remove(key, ptr); } Something like that. I hope someone article will be useful. Thanks for attention.
Source: https://habr.com/ru/post/337594/
All Articles