Wolfenstein 3D pixel-by-pixel fill
In the id Software code, there are at times incomparable pearls. The most famous is, of course, 0x5f3759df , which was honored with even a xkcd comic . Here we will talk about filling the screen: the pixels are painted one by one in a random order, without repetitions. How is this done?

The frontal solution would be to use a random number generator and check whether it is still not painted before filling each pixel. This would be extremely inefficient: by the time the last empty pixel remains on the screen, it will take about 320 × 200 RNG calls to “get” into it. (Recall that Wolfenstein 3D worked at 286 at a frequency of 12 MHz!) Another front-end solution would be to make a list of all 320 × 200 possible coordinates, shuffle it (you can even in advance, and paste it into the code already shuffled), and paint over the pixels in the list; but this would require at least 320 × 200 × 2 = 125KB of memory — one-fifth of the computer’s total memory! (Remember that 640KB should have been enough for anyone ?)
')
Here's how this pixel-by-pixel fill is actually implemented: (the code is a bit simplified compared to the original)
What the hell is going on here?
For those who find it difficult to understand the 8086 assembly code, here’s an equivalent code on pure C:
Simply put:
This “magic” is called a linear feedback shift register : to generate each next value, we push one bit to the right, and slide a new bit to the left, which is obtained as a result of xor. For example, a four-bit RLOS with “taps” on the zero and second bits, the xor of which is set by the bit shifted to the left, looks like this:

If we take the initial value 1, then this RLOS generates five other values, and then it loops: 0 0 0 1 → 1 0 0 0 → 0 1 0 0 → 1 0 1 0 → 0 1 0 1 → 0 0 1 0 → 0001 ( underlined bits used for xor). If we take the initial value that is not involved in this cycle, we get another cycle: for example, 0 0 1 1 → 1 0 0 1 → 1 1 0 0 → 1 1 1 0 → 1 1 1 1 → 0 1 1 1 → 0011. It is easy to verify that three four-bit values that are not in either of these two cycles form the third cycle. A zero value always goes into itself, so it is not considered as possible.
Is it possible to choose RSLOS taps so that all possible values form one big cycle? Yes, if in the field modulo 2 we factor the polynomial x N +1, where N = 2 m –1 is the length of the resulting cycle. Omitting hardcore math , let us show how a four-bit RPLOS with taps on the zero and first bits will take all 15 possible values in turn:
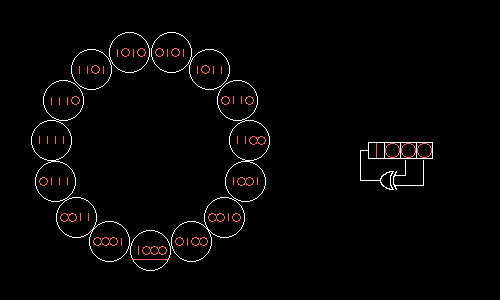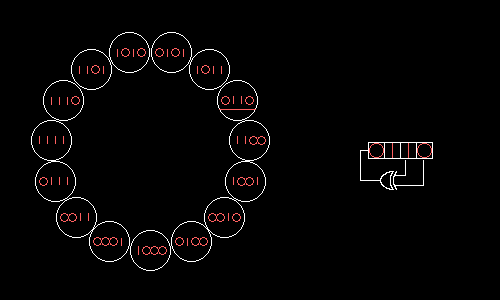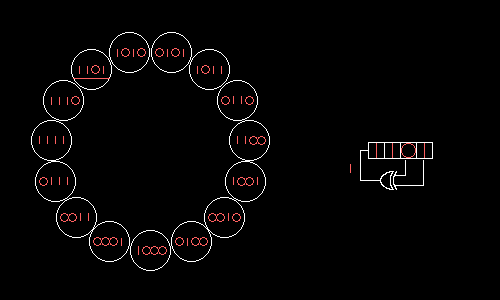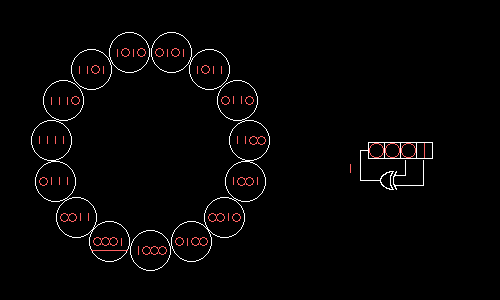
Wolfenstein 3D uses a 17-bit RSLOS with taps on the zero and third bits. This RLOS could be implemented head-on for seven logical operations:
This implementation is called the Fibonacci configuration. Equivalent to her "Galois configuration" allows you to perform all the same for three logical operations:
If you notice that the most significant bit after the shift is guaranteed to be zero, then copying and xor can be combined into one operation:
The value in the “Galois configuration” compared to the “Fibonacci configuration” is cyclically shifted by three bits: the initial value 1 in the Galois configuration (used in the Wolfenstein 3D code) corresponds to the initial value 8 in the Fibonacci configuration. The second LOCR value will be 0x12000, corresponding to 0x10004 in the Fibonacci configuration, and so on. If one of the sequences takes all possible (nonzero) values, then the second one also takes all these values, albeit in a different order. Due to the fact that the zero value for the RLOS is not achievable, one is subtracted from the value of the y coordinate in the code — otherwise the pixel (0.0) would never be painted over.
In conclusion, the author of the original article mentions that out of 2 17 –1 = 131071 values generated by this RLOS, only 320 × 200 = 64000 are used, i.e. slightly less than half; every second generated value is discarded, i.e. the generator runs at half the available speed. For the needs of Wolfenstein 3D, a 16-bit RLOS would suffice, and then you would not have to bother with processing a 32-bit

The frontal solution would be to use a random number generator and check whether it is still not painted before filling each pixel. This would be extremely inefficient: by the time the last empty pixel remains on the screen, it will take about 320 × 200 RNG calls to “get” into it. (Recall that Wolfenstein 3D worked at 286 at a frequency of 12 MHz!) Another front-end solution would be to make a list of all 320 × 200 possible coordinates, shuffle it (you can even in advance, and paste it into the code already shuffled), and paint over the pixels in the list; but this would require at least 320 × 200 × 2 = 125KB of memory — one-fifth of the computer’s total memory! (Remember that 640KB should have been enough for anyone ?)
')
Here's how this pixel-by-pixel fill is actually implemented: (the code is a bit simplified compared to the original)
boolean FizzleFade(unsigned width, unsigned height) { unsigned x, y; long rndval = 1; do // while (1) { // seperate random value into x/y pair asm mov ax, [WORD PTR rndval] asm mov dx, [WORD PTR rndval+2] asm mov bx, ax asm dec bl asm mov [BYTE PTR y], bl // low 8 bits - 1 = y xoordinate asm mov bx, ax asm mov cx, dx asm mov [BYTE PTR x], ah // next 9 bits = x xoordinate asm mov [BYTE PTR x+1], dl // advance to next random element asm shr dx, 1 asm rcr ax, 1 asm jnc noxor asm xor dx, 0x0001 asm xor ax, 0x2000 noxor: asm mov [WORD PTR rndval], ax asm mov [WORD PTR rndval+2], dx if (x>width || y>height) continue; // copy one pixel into (x, y) if (rndval == 1) // entire sequence has been completed return false ; } while (1); } What the hell is going on here?
For those who find it difficult to understand the 8086 assembly code, here’s an equivalent code on pure C:
void FizzleFade(unsigned width, unsigned height) { unsigned x, y; long rndval = 1; do { y = (rndval & 0x000FF) - 1; // 8 - 1 = y x = (rndval & 0x1FF00) >> 8; // 9 bits = x unsigned lsb = rndval & 1; // rndval >>= 1; if (lsb) // = 0, xor rndval ^= 0x00012000; if (x<=width && y<=height) copy_pixel_into(x, y); } while (rndval != 1); } Simply put:
rndvalstarts with 1;- each time we divide the value of
rndvalinto x and y coordinates, and paint over the pixel with these coordinates; - each time we shift and xor-them
rndvalwith an incomprehensible "magic constant"; - when
rndvalsomehow returns to the value 1 - it’s ready, the whole screen is flooded.
This “magic” is called a linear feedback shift register : to generate each next value, we push one bit to the right, and slide a new bit to the left, which is obtained as a result of xor. For example, a four-bit RLOS with “taps” on the zero and second bits, the xor of which is set by the bit shifted to the left, looks like this:
If we take the initial value 1, then this RLOS generates five other values, and then it loops: 0 0 0 1 → 1 0 0 0 → 0 1 0 0 → 1 0 1 0 → 0 1 0 1 → 0 0 1 0 → 0001 ( underlined bits used for xor). If we take the initial value that is not involved in this cycle, we get another cycle: for example, 0 0 1 1 → 1 0 0 1 → 1 1 0 0 → 1 1 1 0 → 1 1 1 1 → 0 1 1 1 → 0011. It is easy to verify that three four-bit values that are not in either of these two cycles form the third cycle. A zero value always goes into itself, so it is not considered as possible.
Is it possible to choose RSLOS taps so that all possible values form one big cycle? Yes, if in the field modulo 2 we factor the polynomial x N +1, where N = 2 m –1 is the length of the resulting cycle. Omitting hardcore math , let us show how a four-bit RPLOS with taps on the zero and first bits will take all 15 possible values in turn:

Wolfenstein 3D uses a 17-bit RSLOS with taps on the zero and third bits. This RLOS could be implemented head-on for seven logical operations:
unsigned new_bit = (rndval & 1) ^ (rndval>>3 & 1); rndval >>= 1; rndval |= (new_bit << 16); This implementation is called the Fibonacci configuration. Equivalent to her "Galois configuration" allows you to perform all the same for three logical operations:
a → b → c → d → e → f → g → h → i → j → k → l → m → n → o → p → q ↑ Fibonacci ↓ ↓ · ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← o → p → q → ^ → a → b → c → d → e → f → g → h → i → j → k → l → m → n ↑ ↑ Galois ↓ · ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ← ·
- move the value to the right;
- copy the extended bit (n) to the highest position;
- xor-im this bit with the 13th (q).
If you notice that the most significant bit after the shift is guaranteed to be zero, then copying and xor can be combined into one operation:
unsigned lsb = rndval & 1; rndval >>= 1; if (lsb) rndval ^= 0x00012000; - as we see in the Wolfenstein 3D code.The value in the “Galois configuration” compared to the “Fibonacci configuration” is cyclically shifted by three bits: the initial value 1 in the Galois configuration (used in the Wolfenstein 3D code) corresponds to the initial value 8 in the Fibonacci configuration. The second LOCR value will be 0x12000, corresponding to 0x10004 in the Fibonacci configuration, and so on. If one of the sequences takes all possible (nonzero) values, then the second one also takes all these values, albeit in a different order. Due to the fact that the zero value for the RLOS is not achievable, one is subtracted from the value of the y coordinate in the code — otherwise the pixel (0.0) would never be painted over.
In conclusion, the author of the original article mentions that out of 2 17 –1 = 131071 values generated by this RLOS, only 320 × 200 = 64000 are used, i.e. slightly less than half; every second generated value is discarded, i.e. the generator runs at half the available speed. For the needs of Wolfenstein 3D, a 16-bit RLOS would suffice, and then you would not have to bother with processing a 32-bit
rndval on a 16-bit processor. The author suggests that id Software programmers simply could not find a suitable combination of “taps” that would give a maximum 16-bit cycle. It seems to me that he greatly underestimates them :-) The fact is that in order to divide a 16-bit value into x and y coordinates, it would have to be divided with the remainder by 320 or 200, and the cost of such a division operation would be more than compensated all acceleration from the transition to a 16-bit lasc.Source: https://habr.com/ru/post/337036/
All Articles