Cryptoalgorithms. Classification in terms of the number of keys

On Habrahabr, about 1000 articles are somehow related to encryption, but sometimes there is a situation when information on a particular algorithm is quickly needed.

Instead of the preface

Initially, this was supposed to be a cycle of 3 publications, but during the publication of the first and second in the comments I was asked to make one general article.
Unfortunately, it took more time, but now I am presenting you a list of about 50 cryptoalgorithms, which is a directory with a brief description of the algorithms, as well as their implementation in some places.

Some algorithms are well known, some are frankly exotic. But these are exactly the algorithms that seemed interesting to me. Perhaps somewhere the emphasis is not on the familiar to all things. , but as they say the taste and color are all different markers. And that one way or another studied in the profile of the university and for which information was most often needed. So to say a brief summary of the student.
')
Special thanks to apashkova for help and editing.
Thank you in advance for your feedback and suggestions.
UPD!
On the advice of Lafter posting a warning.

Attention! Many of the above algorithms are unsafe, outdated, etc., so their use remains entirely on your conscience. In the future, when finalizing the classification, notes will be added directly to each algorithm indicating its safety or lack thereof.

CA typing

So, I present to you an article in which are collected, known and not very, cryptographic algorithms. We will make a reservation that the article does not pretend to innovation, or uniqueness. Rather, a quick reference guide, someone even calls it bedside reading. There are various classifications of cryptographic algorithms, for example, such:


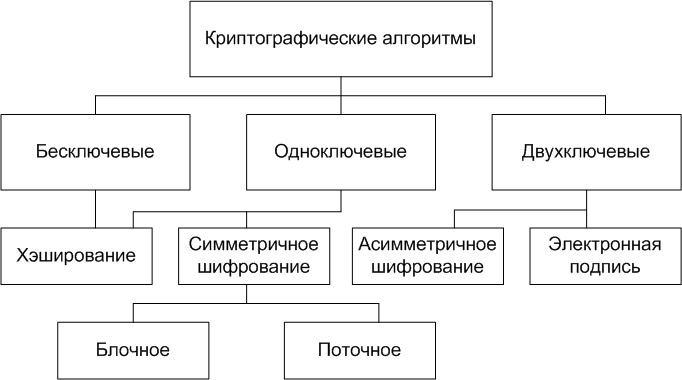
For convenience, I will use the division into groups by the number of keys:

1. Keyless KA - do not use any keys in the calculations;
2. Single-key spacecraft - work with one key parameter (secret key);
3. Two-key satellites - at various stages of operation, two key parameters are used in them: the secret key and the public key.

Keyless KA

md2 / 4/5/6

MD2 is a cryptographic hash function developed by Ronald Rivest in 1989 and described in RFC 1319. At the input, a message is of arbitrary length. The size of the hash is 128 bits.

As braindamagedman wrote about MD5 and MD6 in his time:

The MD5 algorithm was once very popular, but the first prerequisites for hacking appeared in the late nineties, and now its popularity is rapidly falling.

The MD6 algorithm is a very interesting algorithm from a constructive point of view. He was nominated for the SHA-3 competition, but, unfortunately, the authors did not have time to bring him up to standard, and this algorithm is missing from the list of candidates who passed in the second round.

Tiger

A cryptographic hash function developed by Ros Anderson and Eli Beham in 1995. Tiger was designed for especially fast execution on 64-bit computers. Tiger has no patent restrictions, it can be used freely with both the reference implementation and its modifications. The size of the hash value is 192 bits (Tiger / 192), although shorter versions are also available for compatibility with SHA-1 (Tiger / 160) and with MD4, MD5, RIPEMD, Snefru (Tiger / 128). The speed of operation is 132 Mbps (tested on a single processor Alpha 7000, model 660). On modern processors it is much faster (even when tested on 32-bit AMD Sempron 3000+, the speed is about 225 Mbps).

The second version of Tiger2 was also implemented — it differs from the main one only by a different bit addition algorithm, similar to MD5 / SHA-1. Test vectors are available for Tiger2.

Sha-1/2

Algorithm of cryptographic hashing. Described in RFC 3174. For an input message of arbitrary length (maximum 22 ^ 64-1 bits, which is approximately 2 exabytes), the algorithm generates a 160-bit hash value, also called message digest. Used in many cryptographic applications and protocols. Also recommended as a major for government agencies in the United States. The principles underlying SHA-1 are similar to those used by Ronald Rivest in the design of MD4.

SHA-3

A variable-bit hashing algorithm developed by a group of authors led by Yoan Dayman, co-author of Rijndael, the author of MMB, SHARK, Noekeon, SQUARE and BaseKing ciphers. On October 2, 2012, Keccak became the winner of a cryptographic algorithm competition held by the US National Institute of Standards and Technology. On August 5, 2015, the algorithm was approved and published as a FIPS 202 standard. In software implementation, the authors state 12.5 cycles per byte when performed on PCs with an Intel Core 2. However, in hardware implementations, Keccak was much faster than all other finalists. The SHA-3 algorithm is built on the principle of a cryptographic sponge.

Ripemd

A cryptographic hash function developed at the Catholic University of Louvain by Hans Dobbertin (Hans Dobbertin), Anton Bosselaers (Antoon Bosselaers) and Bart Prenel (Anton Bosellar). For an arbitrary input message, the function generates a 160-bit hash value, called a message digest. RIPEMD-160 is an improved version of RIPEMD, which, in turn, used the principles of MD4 and is comparable in performance to the more popular SHA-1.

There are also 128-, 256-, 320-bit versions of the algorithm, with corresponding names.

Haval

A cryptographic hash function developed by Yuliang Zheng, Josef Pieprzyk and Jennifer Seberry in 1992. For an arbitrary input message, the function generates a hash value, called message digest, which can be 128, 160, 192, 224, or 256 bits long. The number of iterations is variable, from 3 to 5. The number of rounds at each iteration is 32. It is a modification of MD5.

Now it's time for single-key spacecraft.

Rijndael

Also known as Advanced Encryption Standart, a symmetric block encryption algorithm. The size of one block. 128 bits, keys 128/192/256, adopted by the standard by the US government according to the results of the AES competition.

Came to replace the algorithm DES (about him later). The specification was published on November 26, 2001. May 26, 2002 was declared an encryption standard. As of 2009 is one of the most common symmetric encryption algorithms.

An interesting fact, the 128 key provides 340 aneccillion possible combinations.

Des

The symmetric encryption algorithm developed by IBM and approved by the US government in 1977 as the official standard (FIPS 46-3). The block size for DES is 64 bits. The algorithm is based on a Feistel network with 16 cycles (rounds) and a key having a length of 56 bits. The algorithm uses a combination of non-linear (S-blocks) and linear (permutations E, IP, IP-1) transformations. For DES recommended several modes:

• ECB (English electronic code book) - “electronic code book” mode (simple replacement);
• CBC (English cipher block chaining) - block coupling mode;
• CFB (English cipher feed back) - ciphertext feedback mode;
• OFB (English output feed back) - output feedback mode.
• A direct development of DES is currently the Triple DES (3DES) algorithm. In 3DES, encryption / decryption is performed by running the DES algorithm three times.

MMB cipher

From eng. modular multiplication-based block cipher (modular block cipher using multiplication) is a block encryption algorithm based on a multiplication operation in a finite group.

A block cipher based on a multiplication operation in a finite group (MMB) is a block cipher developed by Joan Dimene in 1993 as an improvement to the IDEA cipher. The main innovation of this cipher is the use of cyclic multiplication in the group Z2n − 1. The creators of the cipher offered to make n = 32, so the multiplication will be done in the group Z4294967295. It is also worth noting that the length of the words with which operations will be performed is equal to n, that is, 32 in this case. The main goal that was pursued during the creation of this cipher is to create a cipher resistant to differential cryptanalysis. The shortcomings in the key schedule were discovered by Eli Beham, which, in combination with the fact that the cipher was not protected from linear cryptanalysis, led to the use of other ciphers, for example, the 3-Way cipher.

Baseking

In BaseKing cryptography, a block cipher developed in 1994 by Joan Daemen.

He is very closely associated with 3-WAY; indeed, they are variants of the same general encryption technique.

BaseKing has a block size of 192 bits, which is two times longer than 3-WAY. The key length is also 192 bits.

In his thesis, Daemen presented an extensive theory of block cipher, as a fairly general cipher algorithm made up of many reversible transformations that can be chosen with considerable freedom. He discussed the security of this general scheme against known attacks, and gave two specific examples of ciphers consisting of specific choices for variable parameters. These ciphers are 3-WAY and BaseKing. BaseKing is susceptible to the same kind of attack as 3-WAY. Daemaen, Peeters, and Van Assch also demonstrated potential vulnerability to differential analysis, along with a small number of methods to increase BaseKing’s resistance to such an attack.

NOEKEON

A family of two block ciphers designed by Joan Dayman, Michaël Peeters, Gilles Van Assche and Vincent Raimén and represented in the NESSIE research project. Two ciphers are NOEKEON in direct mode (direct mode) and indirect mode (indirect mode). The modes differ only in the key expansion procedure.

The key length in NOEKEON is 128 bits. In each round, NOEKEON uses a sequence of transformations that are inverse to themselves, which can easily be implemented in hardware or software, and even in such, where there is the possibility of an attack on third-party channels. The cipher is compact in implementation in various programming languages, works quickly on various hardware, and is very effective in a wide range of platforms. However, NOEKEON did not meet the requirements of the Wide Trail Design Strategy, which was shown by a cryptanalysis conducted by Lars Knudsen and Håvard Raddum in April 2001. Knudsen and Raddum showed that this cipher could be based on linked keys, due to which the cipher was not selected in NESSIE project.

Both modes of the Noekeon algorithm were accepted for consideration in the framework of the NESSIE competition. Both modes were subject to attack based on the associated keys, which cryptologists Lars Knudsen and Håvard Raddum offered in their work. In addition, they also proved that the criteria for creating replacement tables in the Gamma operation do not contribute to the high reliability of the algorithm: when generating the replacement table, the resulting algorithm with about 86% probability will be subject to linear and / or differential cryptanalysis. It was also shown that it is very likely to find related keys. These reasons were enough for Noekeon’s absenteeism in the second round of the contest.

DFC

Decorrelated Fast Cipher is a block symmetric cryptoalgorithm created in 1998 jointly by the cryptographers of the Paris Higher Normal School, the National Center for Scientific Research (CNRS) and the telecommunications giant France Telecom under the guidance of well-known cryptologist Serge Vodenet (Eng.), Specifically to participate in the AES competition. It belongs to the PEANUT (Pretty Encryption Algorithm with n-Universal Transformation) cipher family.
Block cipher with a long block of 128 bits, representing the 8-round Network Feistel.

A 64-bit encryption function is used, with eight different round bits of 128 bits each, derived from one source encryption key. Each round, the encryption function uses the left half of the source text (block) and two 64-bit keys, which are the half of the corresponding round, to obtain 64-bit ciphertext. The resulting encrypted left half of the block is added to the right. Then, according to the concept of the Feistel network, the left and right parts of the block are swapped. Decryption is the same as encryption using round keys in reverse order. The length of the original encryption key is not limited to the three fixed sizes provided by the AES competition (128, 192 and 256 bits), and can be of variable size from 0 to 256 bits.

DECIM

Decim is a stream cipher based on RSLOS, developed by Combe Burbain, Oliver Billet, Ann Cantus, Nicolas Courtois, Blandin Debre, Henry Gilbert, Louis Gubin, Alin Goucher, Louis Granboulon, Sederic Lard, Marin Minier, Thomas Pornin and Hervamp Sibes. Specialized for hardware implementation. Patented It was presented in the project eSTREAM, where it did not go beyond the third stage.

The most important requirement for ciphers - resistance to various types of attacks. Algebraic attacks are one of the most serious security threats to stream ciphers. If the relationship between the combination of the secret key bits and the gamma bit generated by it is simple or easily predictable, then finding the algebraic dependencies between the secret key bit combination and the key stream bit (gamma) is also a simple task. To complicate the relationship between the combination of the secret key bits (or the combination of the initial state of the RSLOS generated by the secret key) and the key stream bits (gamma), the nonlinear filtering function of the secret key bits combination and the desynchronization mechanism between the secret key bits and the key stream bits (gamma ). Both of these mechanisms (the nonlinear filtering function and the desynchronization mechanism between the combination of the RSLOC bits and the bits of the key stream) are the basis of the work and the main means of preventing the cryptanalytic attacks of the Decim cipher.
The start of the Decim stream cipher begins with the input of an 80-bit private key and a 64-bit public key (Initialization Vector). Then, using certain linear combinations of the K bits and IV bits, using the nonlinear filtering function F and applying the ABSG sampling mechanism, the initial state of the 192-bit RSLOS is calculated. After performing all these operations, the keystream generation begins. $$$z = (zt) | t >> 0$ and filling it with a special buffer BUFFER, used to ensure the continuous issuance of bits $$$zt$ to the output of the cipher, where they are added modulo two with a binary sequence of plaintext characters.

MICKEY

Stream encryption algorithm. There are two variants of this algorithm - with a key length of 80 bits (MICKEY) and 128 bits (MICKEY-128). It was developed by Steve Babbage and Matthew Dodd in 2005 for use in systems with limited resources. This algorithm has a simple hardware implementation with a high degree of security. It uses irregular clocking of shift registers, as well as new methods that provide a sufficiently long period and pseudo-randomness of the key sequence and resistance to attacks. The MICKEY algorithm participated in the eSTREAM competition project organized by the eCRYPT community. The current version of the algorithm is 2.0. She entered the eCRYPT portfolio as a stream cipher for hardware implementation.

The maximum length of a key sequence obtained using one pair (K, IV) is 240 bits. However, 240 such sequences are allowed when using one K, provided that IV is chosen different for each new sequence.

SC2000

Symmetric block cryptoalgorithm developed by Fujitsu and the University of Tokyo in 2000. The algorithm uses a 128-bit block and a key length of 128 to 256 bits (compatible with the AES standard and supports typical key lengths - 128/192/256). It was recommended by the CRYPTREC committee in 2003 for use by Japanese government institutions, but in 2013 it was moved to the list of “candidates” in recommended ciphers. He participated in the Nessie competition, but did not get into the second round, although he showed sufficient resistance to attacks - the reason was his too complex structure and fear of the likelihood of hidden vulnerabilities.

SC2000 is a cipher with a mixed structure: it uses elements of the Feistel network and the permutation-permutation network. The algorithm performs 6.5 (for a 128-bit key) and whether 7.5 (for a key length of 192–256 bits) encryption rounds. Each of the rounds consists of queries to the lookup table, adding a key and a keyless two-round Feistel network.
Three replacement tables are used: a 4x4-bit S-Box is used at the beginning of each round, 5x5 bits in size and 6x6 bits inside the Feistel network.

The key expansion in the SC2000 algorithm is performed in two stages: the intermediate key is generated based on the secret symmetric key, then the required number of extended key fragments is calculated from the intermediate key.

One round of the cipher is rather complicated and consists of the following operations: The input 128-bit value is divided into 4 sub-blocks of 32 bits each, the 32-bit fragment of the extended key is superimposed on each of them by the XOR operation. Operation T is performed, which breaks a data block into 32 sub-blocks of 4 bits each.

Each 4-bit sub-block passes through the S4 lookup table, which looks like this: (2,5,10,12,7,15,11,13,6,0,9,4,8,3,14)

Next, the data block is divided into 32-bit sub-blocks using the operation T ', inverse to operation T. The XOR operation performs the imposition of four other extended key fragments. The values ​​of the first pair of sub-blocks are transmitted to the input of function F. As a result of the execution of this function, two 32-bit values ​​are obtained, which are superimposed on the first two sub-blocks by XOR. The first pair of sub-blocks is reversed with the second pair of sub-blocks, then the last transformation step is repeated.

RC4

Also known as ARC4 or ARCFOUR (alleged RC4) is a stream cipher widely used in various information security systems in computer networks (for example, in SSL and TLS protocols, wireless network security algorithms WEP and WPA).

The cipher was developed by RSA Security, and a license is required to use it.
The RC4 algorithm, like any stream cipher, is built on the basis of a pseudo-random bit generator. A key is written to the generator input, and pseudo-random bits are read at the output. The key length can be from 40 to 2048 bits. The bits generated are evenly distributed.

The main advantages of the cipher:

• high speed;
• variable key size.

RC4 is quite vulnerable if:

• no random or related keys are used;
• one keystream is used twice.

These factors, as well as the way they are used, can make a cryptosystem insecure (for example, WEP).

Further implementation of Illivion .

RC5

Block cipher developed by Ron Rivest of RSA Security Inc. with a variable number of rounds, block length and key length. This expands the scope of use and simplifies the transition to a stronger version of the algorithm.

There are several different variants of the algorithm in which the transformations in the “half-rounds” of the classic RC5 are slightly modified. The classical algorithm uses three primitive operations and their inversions:

1. modulo addition
2. bitwise exclusive OR (XOR)
3. cyclic shift operations by a variable number of bits.

The main innovation is the use of a shift operation for a variable number of bits that were not used in earlier encryption algorithms. These operations are performed equally fast on most processors, but at the same time they significantly complicate the differential and linear cryptanalysis of the algorithm.

RC5 encryption consists of two steps. The key expansion procedure and encryption directly. For decryption, first the key expansion procedure is performed, and then the operations inverse to the encryption procedure.

Rabbit

High-speed stream cipher first introduced in February 2003 at the 10th FSE Symposium. In May 2005, he was sent to eStream, the goal of which was to create European standards for streaming encryption systems.

Rabbit developers are Martin Boesgaard, Mette Vesterager, Thomas Pedersen, Jesper Christiansen and Ove Scavenius.

Rabbit uses a 128-bit key and a 64-bit initialization vector. The cipher was developed for use in software as having high encryption speed. At the same time, the encryption speed could reach 3.7 cycles per byte (CPB) for the Pentium 3 processor and 10.5 cycles per byte for the ARM7. However, the cipher also turned out to be fast and compact when implemented in hardware.

The main component of the cipher is a bitstream generator that encrypts 128 bits of the message per iteration. The advantage of the cipher is to thoroughly mix its internal states between two successive iterations. The mixing function is completely based on the arithmetic operations available on modern processors, that is, S-substitution blocks and search tables are not needed to implement the cipher.

The authors of the cipher provided a complete set of technical descriptions on the Cryptico home page. The cipher is also described in RFC 4503. Cryptico had a patent for the cipher, and for many years a license was required to use the cipher for commercial purposes. However, on October 6, 2008 the cipher was allowed to be used for any purpose for free.

Newdes

In cryptography, a symmetric block cryptographic algorithm developed by Robert Scot as a replacement for the DES standard in 1985 with the goal of introducing a more reliable cipher with a secure key size of 120 bits.

NewDES, although it has a derived name, has a completely different structure, is much simpler than DES, is easy to implement programmatically and does not include bitwise permutations, all operations are performed with bytes. The algorithm uses a replacement table of 256 elements, in a single round 8 modulo 2 addition and substitution operations are performed using the F function - replacements using a substitution table.

The key schedule in the first edition was rather weak and was corrected in the editorial NewDES-96. As it turned out, the NewDES algorithm is less resistant to cryptanalysis than the DES algorithm, although a brute force attack on NewDES-96 is almost impossible and the algorithm in this edition is much safer.

Salsa20

The stream encryption system developed by Daniel Bernstein (English) Russian. The algorithm was presented at the “eSTREAM” competition, the purpose of which was to create European standards for encrypting data transmitted by postal systems. The algorithm became the winner of the competition in the first profile (stream ciphers for software applications with high bandwidth).

The Salsa20 cipher uses the following operations:

1. addition of 32-bit numbers;
2. bitwise modulo 2 (xor);
3. bit shifts.

The algorithm uses a 20-cycle hash function. Its main transformations resemble the AES algorithm.

Sosemanuk

Sosemanuk is a new symmetric software-oriented stream cipher, according to the Profile 1 "ECRYPT call for stream cipher primitives". Key length ranges from 128 to 256 bits. The initial value is set to 128 bits. As stated, any key length reaches 128-bit protection. The Sosemanuk cipher uses both the basic principles of the SNOW 2.0 stream cipher and some of the transformations derived from the SERPENT block cipher. Sosemanuk aims to improve SNOW 2.0 both in terms of security and efficiency. In particular, it uses the fast IV-setup procedure. It is also necessary to reduce the number of static data in favor of improving performance on several architectures (platforms).

The Sosemanuk cipher uses both the basic principles of the SNOW 2.0 stream cipher (“Snow” - English “snow”) and some transformations (transformations) derived from the SERPENT block cipher (“SERPENT” - English “snake”). For this reason, its name must be associated with the snake, and with the snow. However, it is well known that snow snakes do not exist, as snakes either fall asleep or move to warm regions for the time of winter. In addition, Sosemanuk - a popular sport, common among the tribes of Eastern Canada. The idea of ​​the game is to throw a wooden stick along the snow coast as much as possible. The name comes from the adverb of nations and contains a comparison of the stick in the snow with a snake. "Kwakweco-cime win" is one of the names of this game, but it does not sound appropriate for the name of the cipher.

Trivium

A symmetric synchronous stream encryption algorithm, focused primarily on a hardware implementation with a flexible balance between the speed of operation and the number of elements, which also has the possibility of a fairly efficient software implementation.

The cipher was introduced in December 2008 as part of the portfolio of the European project eSTREAM, by profile 2 (hardware-oriented ciphers). The authors of the cipher are Christoph De Kannier and Bart Prenel.

This stream cipher generates up to $$$2 ^ {64}$ output bit of 80 key bits and 80 bit IV (initialization vector). This is the simplest cipher of the eSTREAM project, which shows excellent crypto-stability results.

Trivium is included in the ISO / IEC 29192-3 standard as a lightweight stream cipher.
The initial state of Trivium consists of 3 shift registers of a total length of 288 bits. Each clock cycle there is a change in the bits in the shift registers by a non-linear combination of forward and feedback. To initialize the cipher, the key K and the initialization vector IV are written in 2 of 3 registers and the algorithm is executed for 4x288 = 1152 times, which guarantees the dependence of each bit of the initial state on each bit of the key and each bit of the initialization vector.

After passing through the initialization stage, each clock cycle generates a new member of keystream Z, which passes the XOR procedure with the next member of the text. The decryption procedure occurs in the reverse order - each member of the ciphertext passes the XOR procedure with each member of the key stream Z.

VMPC

This is a stream cipher used in some information security systems in computer networks. The cipher is designed by cryptographer Bartosh ultak (Polish: Bartosz Żółtak, Eng. Bartosz Zoltak) as an enhanced version of the popular RC4 cipher. The VMPC algorithm is built just like any stream cipher based on a pseudorandom bit generator parametrized by a key. The main advantages of the cipher, like RC4, are high speed, variable key size and initialization vector (from 128 to 512 bits inclusive), ease of implementation (literally several dozen lines of code).

The base of the cipher is a pseudo-random number generator, the base of which is a one-way irreversible VMPC function (English Variably Modified Permutation Composition).

Frog

Symmetric block encryption algorithm with unorthodox structure, one of the participants of the American competition AES, the development of the Costa Rican company TecApro Internacional.

The FROG algorithm was created in 1998 by three specialists from the Tecnologia Apropriada company (TesArgo) from a small African state of Africa (unidentified by its developments in cryptography): Dianelos Georgoudis, Damian Jlepy (Damian Leroux), Dianelos Georgoudis, Damian Jlepy (Damian Leroux), Dianan Georgoudis, Damian Jlepy (Damian Leroux). Simon Chaves).

The announced version of the cipher complies with the AES requirements, having a block equal to 128 bits and a key 128, 192 or 256 bits long. The algorithm itself, in theory, allows keys from 40 to 1000 bits in length.

The FROG cipher was put up for the competition by the international company TecApro Internacional, registered in Costa Rica. Algorithm developers - D. Georgoudis, D. Leroux and B. Chaves - people, to put it mildly, little known in the cryptographic world. According to the authors, FROG is “a new cipher with an unorthodox structure”. The basis of the cipher strength is the secret internal key of a complex structure, and the encryption / decryption operations themselves are extremely simple.
In August, the TWOFISH team (Wagner, Ferguson and Schneier) showed that the FROG cipher key can be opened with a workload of about 257.

As for the strength of ciphers, this indicator is much more difficult to verify. During the preliminary assessment stage of the first round, a significant number of cryptanalytic results were presented on the NIST website and directly at the AES2 conference, one way or another “staining” the reputation of almost all candidate ciphers. However, if we do not speak about the obvious outsiders LOKI, FROG, MAGENTA and HPC, then no obvious weaknesses in the algorithms were found.

NUSH

Block symmetric encryption algorithm developed by Anatoly Lebedev and Alexey Volchkov for Russian company LAN Crypto.

NUSH has several different options that have a different block size (64, 128, 256 bits), a different number of rounds (depending on the block size is 36, 128 or 132 rounds) and uses a key length of 128, 192 or 256 bits. The algorithm does not use S-blocks, but only such operations as AND, OR, XOR, modulo addition and cyclic shifts. Before the first and after the last round, the key is “whitened”.

This algorithm was put forward in the NESSIE project, but was not chosen, as it was shown that linear cryptanalysis can be more effective than a brute force attack.
Based on the encryption algorithm, you can build other algorithms. Several of them are outlined in this article.

REDOC

Symmetric block cryptoalgorithm developed by Michael Wood in 1990 for the company Cryptech and received the name REDOC II. All operations - substitutions, permutations, XOR are performed with bytes, which allows it to be effectively implemented programmatically. The algorithm uses key and source plaintext-dependent table sets (S-blocks), using changing table functions. The algorithm distinguishes the use of masks, i.e. numbers derived from the key table. Masks are used to select tables for a specific function of a particular round. It uses both the mask value and the data value.
Brute force is considered to be the most effective way to open a key; to achieve the goal, 2160 operations are required. Practically the only effective cryptoanalysis was the opening of one of the rounds of the algorithm by Thomas Kuzik, but it was not possible to expand the opening for further rounds. With the help of 2300 open texts, a cryptanalysis of one of the rounds by Shamir and Biham was conducted, after 4 rounds 3 mask values ​​were obtained, but this did not bring success as such, and at the moment the algorithm is considered cryptographic.

There is also a significantly simplified version of the algorithm - REDOC III, created by Michael Wood. An 80-bit block is used, the key length is variable, and can reach 20,480 bits. Permutations and substitutions are excluded, all operations on the block and key are based only on the use of XOR, due to which the encryption speed is significantly increased to the detriment of resistance to differential cryptanalysis. The algorithm is based on 256 10-byte keys, generated on the basis of the secret key, and two 10-byte mask blocks, obtained on the basis of the XOR 128 128-byte keys. For the successful restoration of both masks of the REDOC III algorithm, 223 open texts are required. This algorithm is simple and fast. On the 3338 megahertz processor 80386, it encrypts data at a speed of 2.75 Mbps. The REDOC II cryptographic system is capable of encrypting 800 kbps at a clock frequency of 20 MHz.

The REDOC II algorithm and its simplified version are patented in the USA.

3-way

This is a symmetric, private-key block cipher developed by Joan Daeman, one of the authors of the Rijndael algorithm (sometimes called AES).

The 3-Way algorithm is an 11-step SP network. A block and a key length of 96 bits are used. The encryption scheme, as is typical for algorithms of the SP-network type, implies an efficient hardware implementation.

Shortly after the publication, a successful cryptanalysis of the 3-Way algorithm was carried out, which showed its vulnerability to the attack based on the associated keys. The algorithm is not patented.

Blowfish

A cryptographic algorithm that implements a symmetric block encryption with a variable key length. Designed by Bruce Schneier in 1993.It is a network of Feistel. Performed on simple and fast operations: XOR, substitution, addition. Is unpatented and freely distributed.

Before the advent of Blowfish, the existing algorithms were either patented or unreliable, and some were kept secret (for example, Skipjack). The algorithm was developed in 1993 by Bruce Schneier as a fast and free alternative to the outdated DES and patented IDEA. According to the author, the design criteria for Blowfish were:

1. speed (encryption on 32-bit processors takes 26 clock cycles);
2. simplicity (due to the use of simple operations that reduce the probability of an error in the implementation of the algorithm);
3. compactness (ability to work in less than 5 KB of memory);
4. custom security (adjustable key length).

The algorithm consists of two parts: key expansion and data encryption. At the key expansion stage, the source key (up to 448 bits in length) is converted into 18 32-bit subkeys and into 4 32-bit S-boxes containing 256 elements. The total amount of keys received is equal to$$$(18+256*4) *32=33344 (18+256*4) *32=33344$ bits or 4168 bytes.

Cast

A symmetrical encryption network based on the Feistel network, which is used in a number of cryptographic protection products, in particular, some versions of PGP and GPG and is also approved for use by the Canadian government.

The algorithm was created in 1996 by Carlisle Adams and Stafford Tavares using the CAST cipher method, which is also used by their other CAST-256 algorithm (the AES candidate algorithm).

CAST-128 consists of 12 or 16 rounds of a Feistel network with a block size of 64 bits and a key length from 40 to 128 bits (but only with an increment of 8 bits). 16 rounds are used when key sizes exceed 80 bits. The algorithm uses 8x16 S-blocks based on bent functions, XOR operations, and modular arithmetic (modular addition and subtraction). There are three different types of round functions, but they are similar in structure and differ only in the choice of the operation to be performed (addition, subtraction or XOR) in different places.

Although CAST-128 is protected by the Entrust patent, it can be used worldwide for commercial or non-commercial purposes for free.

CAST is resistant to differential and linear cryptanalysis. The strength of the CAST algorithm lies in its S-boxes. CAST has no fixed S-boxes and they are newly constructed for each application. The S-block created for a specific CAST implementation never changes again. In other words, S-boxes are implementation dependent, not key dependent. Northern Telecom uses CAST in its Entrust software for Macintosh, PC and UNIX workstations. The S-blocks chosen by them are not published, which, however, is not surprising.
CAST-128 is owned by Entrust Technologies, but is free for both commercial and non-commercial use. CAST-256 is a free available CAST-128 extension that accepts a key size of up to 256 bits and has a block size of 128 bits. CAST-256 was one of the original candidates for AES.

CAST-256 is built from the same elements as CAST-128, including S-boxes, but the block size is doubled and equal to 128 bits. This affects the diffusion properties and protection of the cipher.
RFC 2612 states that CAST-256 can be freely used throughout the world for commercial and non-commercial purposes.

e2

In cryptography, E2 is a symmetric block cipher, which was created in 1998 by NTT and submitted to the AES competition.

Like other AES candidates, E2 operates on 128-bit blocks, using a 128, 192 or 256-bit key. He uses a 12-round network of Feistel. E2 has an input and output transform transform, like using modular multiplication, but the round function itself consists only of the XOR operation and the S-search box. A single 8 × 8-bit S-box is made of an affine transform with discrete exponentiation X127 over a finite field GF (28). NTT adopted many of the special characteristics of E2 in Camellia, which was essentially replaced by E2.

Twofish

Symmetric block encryption algorithm with a block size of 128 bits and a key length of up to 256 bits. Number of rounds 16. Developed by a team led by Bruce Schneier. He was one of the five finalists of the second stage of the AES competition. The algorithm is based on the algorithms of Blowfish, SAFER and Square.

Distinctive features of the algorithm are the use of pre-computed and key-dependent replacement nodes and a complex scan subkey encryption scheme. Half of the n-bit encryption key is used as the encryption key itself, the other is used to modify the algorithm (replacement nodes depend on it).

Twofish was developed specifically to meet the requirements and recommendations of NIST for AES:

1. 128-bit block symmetric cipher
2. The length of the keys 128, 192 and 256 bits
3. No weak keys
4. ( 32- )
5. ( , , - . .).
6. — .

However, it is the complexity of the algorithm structure and, accordingly, the complexity of its analysis for weak keys or hidden connections, as well as the rather slow execution time compared to Rijndael on most platforms, did not play in his favor.

The Twofish algorithm arose from an attempt to modify the Blowfish algorithm for a 128-bit input block. The new algorithm was supposed to be easily implemented by hardware (including using smaller tables), have a more advanced key schedule system and have an unambiguous function F.

As a result, the algorithm was implemented as a mixed Feistel network with four branches, which modify each other using Hadamard's crypto-transform (Pseudo-Hadamar Transform, PHT).

The ability to effectively implement modern (for that time) 32-bit processors (as well as smart cards and similar devices) is one of the key principles guided by the Twofish developers.

For example, in the F function, when calculating PHT and adding with part of the key K, addition is intentionally used instead of the traditional xor. This makes it possible to use the LEA command of the Pentium processor family, which allows calculating the Hadamard transform in one clock cycle$$$(T_0+2T_1+K_2r+9)~mod~2^{32} * (T_0+2T_1+K_2r+9)~mod~2^{32}$ (However, in this case, the code must be compiled for a specific value key).
The Twofish algorithm is not patented and can be used by anyone without any fees or deductions. It is used in many encryption programs, although it has received less distribution than Blowfish.

Xtea

Block cipher algorithm designed to eliminate critical errors of the TEA algorithm. The cipher developers are David Wheeler and Roger Needham (Faculty of Computer Science, University of Cambridge). The algorithm was presented in an unpublished technical report in 1997. The cipher is not patented; it is widely used in a number of cryptographic applications and a wide range of hardware due to extremely low memory requirements and ease of implementation.

Like TEA, the cipher is based on operations with a 64-bit block, it has 32 full cycles, in each full cycle two rounds of the Feistel Network, which means 64 rounds of the Feistel network. However, the number of rounds to achieve better diffusion can be increased at the expense of performance. In addition, XTEA, like TEA, uses a 128-bit key consisting of four 32-bit words K [0], K [1], K [2] and K [3]. XTEA does not have a key planning algorithm in the usual sense. In order to determine which of the four key words to use in each round, the algorithm uses the constant δ = 9E3779B916. In TEA, there is no such distribution. Another difference from TEA is the permutation of bit operations used in the cipher. Thanks to these improvements, XTEA has not undergone much complication compared to TEA,but at the same time eliminated two major drawbacks of the TEA algorithm:
each key in TEA is equivalent to three others, which means that the effective key length is 126 bits instead of 128, as was intended by the developers;
TEA is susceptible to attacks on related keys. Such an attack may require as few as 223 of the selected plaintext and have a time complexity of 232.

Wake

The auto-key stream encryption algorithm, created by David J Wheeler in 1993. It is an encryption system with medium-rate encryption of blocks. When working requires the use of repetition tables and a large state space. The cipher gamut uses 32-bit words, works in CFB mode — the previous word of the cipher sequence serves as the basis for generating the next one. The algorithm also uses the S-block replacement, consisting of 256 32-bit words, which increases its durability.

The algorithm is unstable to attacks on the selected source text and attacks on selected ciphertexts.

Skipjack

Block cipher developed by the US National Security Agency as part of the Capstone project. After the development of information about the cipher were classified. It was originally intended for use in the Clipper chip to protect audio information transmitted over government telephone networks, as well as mobile and wireless networks. Later the algorithm was declassified.

Skipjack was one of the initiatives proposed by the Capstone project. The project was led by the National Security Agency (NSA) and the National Institute of Standards and Technology (NIST), funded by the US government. The official start date of the initiative is 1993. The encryption algorithm was developed in 1980, and its first implementation was obtained in 1987. The cipher was intended for use in the Clipper chip embedded in the protected equipment. At the same time, Skipjack was used only for encrypting messages, and the key was deposited to be used by authorized bodies - the most discussed aspect of using a cipher - was achieved through a separate mechanism called the Law Enforcement Access Field.

Initially, the project was classified and for this reason was subjected to great criticism. To increase public confidence and evaluate the algorithm, several academic researchers were called upon. Due to the lack of time for independent thorough research, the experts concentrated on studying the description of the development and evaluation of the algorithm presented by the NSA. In addition to this, they, during the month, conducted a series of small tests. The preliminary report on their work (the final report did not follow) indicated three conclusions:

1. Taking into account that the cost of computing power is halved every 18 months, it is only after 36 years that the cost of a Skipjack burglary is brute-force equal to the cost of a DES hack today.
2. The risk of breaking a cipher using faster methods, including differential cryptanalysis, is negligible. The algorithm does not have weak keys and the properties of complementarity.
3. Skipjack's resistance to cryptanalysis does not depend on the secrecy of the algorithm itself.

The cipher was published in open access on June 24, 1998. In August 2016, NIST adopted new principles for the use of cryptographic standards, in which it revoked the Skipjack algorithm certification for government purposes.

Skipjack uses an 80-bit key to encrypt / decrypt 64-bit data blocks. This is an unbalanced network of Feistel with 32 rounds.

Shark

The SHARK algorithm was developed by Vincent Regen and Joan Damen - the future authors of the AES standard, but in collaboration with three other specialists from the Catholic University of Leuven, Belgium. This is a slightly earlier development than the Square algorithm - SHARK was developed in 1995.

The algorithm uses a 128-bit key and a 64-bit block. The SHARK algorithm has conservative parameters and is designed to replace existing ciphers with 64 bit blocks, like IDEA and DES.

There are two options for the SHARK cipher: SHARK-A (English affine transform) and SHARK-E (English exor).
There are attacks only on a modified version of the cipher with 5 rounds. The algorithm itself at the moment can be considered safe.

This algorithm was developed and became the basis of a new, more secure KHAZAD cipher. The Rijndael algorithm can also be considered based on the ideas of the SHARK cipher and its descendant.

Serpent

Designed by Ross Anderson, Eli Beham and Lars Knudsen. Some previous authors' designs were also named after animals, for example, Tiger, Bear.
The algorithm was one of the finalists of the 2nd stage of the AES competition. Like other algorithms that participated in the AES competition, Serpent has a block size of 128 bits and possible key lengths of 128, 192 or 256 bits. The algorithm is a 32-round SP-network, working with a block of four 32-bit words. Serpent was designed so that all operations can be performed in parallel using 32 1-bit "streams".

When developing Serpent, a more conservative approach to security was used than that of other AES finalists, the cipher designers believed that 16 rounds were enough to withstand known types of cryptanalysis, but increased the number of rounds to 32 so that the algorithm could better withstand unknown methods of cryptanalysis.

Having become a finalist in the AES competition, the Serpent algorithm as a result of voting took the 2nd place.
The cipher Serpent is not patented and is in the public domain.

The algorithm was created under the slogan "21st century cryptographic algorithm" for participation in the AES competition. New, untested and untested technologies were not used to create a cipher, which, if adopted, would be used to protect vast amounts of financial transactions and government information. The main requirement for the AES bidders was that the bidder algorithm must be faster than 3DES and provide at least the same level of security: it must have a 128-bit data block and a 256-bit key. A 16-round Serpent would be as reliable as 3DES, but twice as fast. However, the authors decided that for greater reliability it is worthwhile to increase the number of rounds to 32. This made the cipher as fast as DES, and much more reliable than 3DES.

Seal

Symmetric data stream encryption algorithm optimized for software implementation.

Developed at IBM by Phil Rogaway (Eng.) (Eng. Phil Rogaway) and Don Coppersmith (Eng. Don Coppersmith) in 1993. The algorithm is optimized and recommended for 32-bit processors. To work, it requires a cache of several kilobytes and eight 32-bit registers. The encryption speed is about 4 machine cycles per byte of text. A 160-bit key is used for encoding and decoding. To avoid undesirable loss of speed due to slow key processing operations, SEAL performs several transformations with it, resulting in three tables of a certain size.
These tables are used directly to encrypt and decrypt text instead of the key itself.

The algorithm is considered very reliable, very fast and is protected by US patent No. 5454039 from December 1993.

In 1991, Ralph Merkle (Ralph C. Merkle) described the profitability of software-oriented ciphers. In his opinion, the most effective of them were Khufu, FEAL and RC4. However, the ever-increasing needs of customers in reliable cryptography required the search for new and refinement of old solutions.

In the summer of 1992, the development of the first version of the new software-optimized algorithm SEAL 1.0 began. The developers took the basic ideas and the principle of work from the block cipher of Ralph Merkle (English Ralph C. Merkle) Khufu, which seemed to them the most perfect at that time. They decided to achieve the best performance of the project (mainly speed), narrowing the range of equipment on which its implementation is possible. The choice was made in favor of 32-bit machines with at least eight general-purpose registers and a cache of at least 8 KB. In March 1993, it was decided to create a block cipher, but the structure of the family of pseudo-random functions, developed by October of the same year, worked faster, which led the developers to streamline encryption. This structure consisted of four registers, each of which changed its “neighbor” depending on the table,derived from the key. After a number of such modifications, the values ​​of the registers are added to the key sequence, which grows with each iteration until it reaches a certain length. During the development, almost all attention was paid to the internal loop of the algorithm, since the procedure of register initialization and the method of generating tables from the key had little effect on its security. In its final form, the project SEAL 1.0 appeared only in December 1993.since the procedure for initializing the registers and the method of generating tables from the key had little effect on its security. In its final form, the project SEAL 1.0 appeared only in December 1993.since the procedure for initializing the registers and the method of generating tables from the key had little effect on its security. In its final form, the project SEAL 1.0 appeared only in December 1993.

In 1996, Helena Handschuh (Eng.) And Henri Gilbert (Eng.) Described the attacks on the simplified version of SEAL 1.0 and on SEAL 1.0 itself. They took$$$2^{30}$ texts, each with four 32-bit words in length, to find the dependence of a pseudo-random function on a key. As a result, in the next versions of the SEAL 3.0 and SEAL 2.0 algorithm, some improvements and changes were made. For example, in version 1.0, each iteration with a key sequence ended with a modification of only two registers, and in version 3.0, all four were modified. SEAL 3.0 and SEAL 2.0 used the SHA-1 (Secure Hash Algorithm-1) algorithm for generating tables instead of the initial SHA, which made them more resistant to cryptanalysis.

Safer

A family of symmetric block cryptoalgorithms based on a permutation-permutation network. The main contribution to the development of algorithms was made by James Massey. The first version of the cipher was created and published in 1993.

There are several cipher options that differ from each other in the length of the encryption key and the size of the source text blocks.

The first type of algorithm, SAFER K-64, was developed by James Massey for the 1993 California-based Cylinc Corporation. Published in the same year, the algorithm had a block and a 64-bit encryption key. It was recommended for him to use 6 rounds of encryption. However, due to the need to increase the key length to 128 bits (since a weakness was discovered in the original version of the algorithm), Massey developed a new version of the SAFER K-128 cipher, which was published the following year after SAFER K-64. The new algorithm included a key schedule developed by the Singapore Ministry of the Interior and later used by it for various purposes. Also for this algorithm, it was recommended to use 10 (maximum 12) rounds of encryption.

Some time later, in the first versions of the algorithm, some weaknesses revealed by Lars Knudsen and Sean Murphy came to light. This led to the creation of new versions of the algorithm, called SAFER SK-64 and SAFER SK-128, in which the key schedule was changed in accordance with the scheme proposed by Knudsen. A variant with a key length reduced to 40 bits - SAFER SK-40 was also developed. The abbreviation “SK” in the name of the algorithms is decoded as “Strengthened Key schedule”. For new cipher options, it was proposed to use not 6, but at least 8 (maximum 10) encryption rounds.

The SAFER + algorithm was developed in 1998 by the California corporation Cylinc in conjunction with the Armenian Academy of Sciences to participate in the AES competition, where only the first qualifying round was held. This cipher has an input block of 128 bits long and a key size of 128, 192 or 256 bits.

The latest variation of the SAFER algorithm created is SAFER ++, developed by Massey in 2000 and further developed by the SAFER + algorithm. The algorithm took part in the European competition of NESSIE algorithms, where it was presented in two versions: a cipher with a 64-bit block and a 128-bit block. It went into the second phase of the competition, but was not selected into the set of NESSIE-recommended cryptographic primitives. Experts found that the cipher is too slow on all machines except 8-bit (such as smart cards), and the cipher security margin is too small.

SAFER algorithms are not privately owned and are not protected by copyright, that is, they can be used without any restrictions. Since they consist entirely of simple byte operations (with the exception of byte rotation when generating keys), these algorithms can be implemented by processors with a small length.

MISTY1

Block encryption algorithm, created on the basis of the “embedded” Feistel networks in 1995 by cryptologist Mitsuru Matsui together with a group of specialists for Mitsubishi Electric. MISTY is an abbreviation of Mitsubishi Improved Security Technology, as well as the initials of the algorithm creators: Tetsuya Ichikawa, Toshio Tokita and Toshio Tokita, and Atsuhiro Yamagisi and Yee Yaki Yee, who joined the YTC, also the Yakhi-Ying Yi, Yak Yawi, and the Yak-yi Yak-yi Yak Yaki-Yi, who wrote the algorithm. The algorithm was developed in 1995, but was licensed and was published already in 1996.

MISTY1 is a Feistel network with a variable number of rounds (8 is recommended, but it can be any multiple of 4). The algorithm works with 64-bit blocks and uses a 128-bit key. The cipher was the winner among the algorithms that encrypt 64-bit blocks at the European NESSIE competition. As a result of the analysis of the algorithm carried out in the framework of this competition and before it, the experts concluded that this algorithm does not have any serious vulnerabilities (they emphasized that the structure of the algorithm with nested Feistel networks makes cryptoanalysis much more difficult). Similar studies were carried out in the framework of the CRYPTREC project on the choice of cryptoalgorithms for e-government in Japan. The project experts highly appreciated the algorithm MISTY1, concluding that it has a high margin of robustness,The algorithm has a high encryption speed and is very effective for hardware implementation.

MISTY1 patented algorithm. However, the original patent owner, Mitsubishi Electric, announced that it would issue a license to use for free.
MISTY1 was developed based on the theory of "proven security" against differential and linear cryptanalysis. This algorithm was designed to counter various crypto-attacks known at the time of creation.

Since the publication of Misty, a lot of research has been done to evaluate its security level. Some results on the study of the Misty with fewer rounds are presented below.

High order differential cryptanalysis is effectively applied to block ciphers with a small degree. Misty contains 2 look-up tables S7 and S9, both with small ad, 3 and 2, respectively. Therefore, many articles are devoted to differential cryptanalysis of the mystery. The best result was obtained for a 5-level algorithm without FL functions. However, it is the presence of FL functions and wide-bit AND / OR operations in them that makes it difficult to use high order differential cryptanalysis.

Impossible differential analysis is also applicable to block fonts with the same subkey value in each round (or in each nth round). And since MISTY1 has a fairly simple key expansion system, it is natural to consider the applicability of this attack to this algorithm. The best result for such an attack was also obtained when considering an algorithm without FL functions.

The cipher became the winner among the algorithms that encrypt 64-bit blocks at the European NESSIE competition (2000-2003 years). As a result of the analysis of the algorithm carried out in the framework of this competition and before it, the experts concluded that this algorithm does not have any serious vulnerabilities (they emphasized that the structure of the algorithm with nested Feistel networks makes cryptoanalysis much more difficult).

Similar studies were carried out in the framework of the CRYPTREC project on the choice of cryptoalgorithms for e-government in Japan. The project experts highly appreciated the MISTY1 algorithm, concluding that it has a high margin of robustness, the algorithm has a high encryption rate and is very effective for hardware implementation.

There is a modification of this algorithm - MISTY2. However, it was not widely known due to the low level of security.

Also the modification MISTY1, the KASUMI algorithm, became widespread in 2000, becoming the standard for encrypting mobile communications W-CDMA.

KASUMI (from Japanese. 霞 (hiragana か す み, romaji kasumi) - fog, mist) is a block cipher used in 3GPP cellular networks. Also denoted A5 / 3 when used in GSM and GEA3 in GPRS.

KASUMI was developed by the SAGE group (Security Algorithms Group of Experts), which is part of the European Telecommunications Standardization Institute (ETSI). The basis was taken by the existing algorithm MISTY1 and optimized for use in cellular communication.
As cryptanalysts showed in 2010, in the process of changes, the reliability of the MISTY1 algorithm was reduced: KASUMI has vulnerabilities to some types of attacks, whereas MISTY1 is resistant to them.

KASUMI uses a 64-bit block size and a 128-bit key in an 8-round Feistel scheme. Each round uses a 128-bit round key, consisting of eight 16-bit subkeys, obtained from the source key using a fixed subkey key generation procedure.

Mars

AES candidate candidate developed by IBM, which created DES at the time. According to IBM, the 25-year-old cryptanalytic experience of the company is embedded in the MARS algorithm, and along with high cryptographic strength, the cipher allows for efficient implementation even in such limited limits as are typical for smart cards.

Don Coppersmith, one of the authors of the Lucifer (DES) cipher, was famous for several articles on cryptology: improving the structure of S-blocks against differential cryptanalysis, the method of fast matrix multiplication (Coppersmith-Vinograd algorithm), RSA cryptanalysis. In addition to him, the development of the algorithm was attended by: Carolyn Barvik, Edward D'Evignon, Rosario Genaro, Shay Halevi, Charanjit Jutla, Stephen M. Matthias Jr., Luke O’Connor, Mohamed Perrevyan, David Safford, Nevenko Zunich.

According to the rules of the AES contest, participants could make minor changes to their algorithms. Using this rule, the authors of MARSa changed the key expansion procedure, which made it possible to reduce the requirements for non-volatile and RAM. Below is a modified version of the algorithm.

According to the results of the AES competition, MARS reached the final, but lost to Rijndael. After the results were announced (May 19, 2000), the development team made its own opinion about the AES competition, where it gave comments on claims to its brainchild.

Now MARS is distributed worldwide under the royalty-free license. The algorithm is unique in that it used almost all existing technologies used in cryptographic algorithms, namely:

• simple operations (addition, subtraction, exclusion or)
• substitutions using the replacement table
• fixed cyclic shift
• data dependent cyclic shift
• multiplication modulo 232
• key whitening

The use of double-shuffle is a challenge for cryptanalysis, which some attribute to the shortcomings of the algorithm. At the same time, there are currently no effective attacks on the algorithm, although some keys may generate weak plug-ins.

Loki

In cryptography, LOKI89 and LOKI91 are the symmetric key of block ciphers, intended as a possible replacement for the DES (Data Encryption) standard. Ciphers were developed based on the body of the DES analyzing work, and are very similar to DES in structure. Loki's algorithms were named for Loki, the god of mischief in Norse mythology.

LOKI89 was first published in 1990, then simply called "LOKI", by Australian cryptographers Lori Brown, Joseph Pieprzyk, and Jennifer Seberry. LOKI89 was submitted to the European RIPE project for evaluation, but was not selected.

The cipher uses a 64-bit block and a 64-bit key. Like DES, this is a 16-round network of Feistel and has a similar overall structure, but differs from the choice of specific S-boxes, “P-permutations”, and “Expansion permutation”. S-boxes use non-linearity criteria developed by Josef Pieprzyk, making them as “complex” and “unpredicatable” as possible. Their effectiveness was compared with the known design criteria for DES S-boxes. Permutations were designed to “mix” the outputs of the S-boxes as quickly as possible, contributing to the avalanche and completeness of the properties necessary for a good Feistel cipher. However, unlike their equivalents in DES, they are designed to be as clean and simple as possible (in retrospect, perhaps a little too simple), aiding the analysis of the construction.

After the publication of LOKI89, information on new differential cryptanalysis became available, as well as some results of an early analysis by (Knudsen 1993a). This led to the design being changed to become LOKI91.

LOKI 91 was developed in response to attacks on LOKI89 (Brown et al., 1991). The changes included the removal of the start and end key Whitening, the new S-box, as well as minor changes to the key schedule. More specifically, the S-blocks were modified to minimize the chance of seeing different inputs leading to the same output (hook that uses differential cryptanalysis), thereby improving LOKI91's immunity to this attack, as described in detail by the authors of the attack (Biham and Shamir 1991). Changes to the key schedule were designed to reduce the number of “equivalent” or “associated with” keys that led to the selector space for the cipher being reduced.

While the resulting cipher is clearly stronger and safer than LOKI89, there are a number of potential attacks, as described in detail in the work of Knudsen and Biham. Consequently, these ciphers should be considered as scientific efforts to advance the development of block ciphers, and not algorithms to use. A number of citations and published criticisms indicate this goal was achieved.

Idea

Symmetric block data encryption algorithm, patented by the Swiss company Ascom. Known for being used in the PGP encryption software package. In November 2000, IDEA was presented as a candidate for the NESSIE project within the framework of the European Commission IST (Information Societies Technology) program.
The first version of the algorithm was developed in 1990 by Lai Xuejia (Xuejia Lai) and James Massey (James Massey) from the Swiss Institute of ETH Zürich (under a contract with the Hasler Foundation, which later joined Ascom-Tech AG) as a replacement for DES (Data Encryption Standard, a standard for data encryption) and called it PES (Proposed Encryption Standard), the proposed encryption standard. Then, after the publication of the work of Biham and Shamir on differential cryptanalysis of PES, the algorithm was improved in order to enhance cryptographic strength and was named IPES (Improved Proposed Encryption Standard, improved proposed encryption standard). A year later it was renamed IDEA (English International Data Encryption Algorythm).

Since IDEA uses a 128-bit key and a 64-bit block size, the plaintext is divided into blocks of 64 bits. If such a partition is not possible, the last block is supplemented in various ways by a specific sequence of bits. To avoid leakage of information about each individual block, different encryption modes are used. Each initial unencrypted 64-bit block is divided into four sub-blocks of 16 bits each, since all algebraic operations used in the encryption process are performed on 16-bit numbers. IDEA uses the same algorithm for encryption and decryption.
A fundamental innovation in the algorithm is the use of operations from different algebraic groups, namely:

• modulo addition
• multiplication modulo
• bitwise exclusive OR (XOR).

These three operations are incompatible in the sense that:

• no two of them satisfy the distribution law
• no two of them satisfy associative law

The use of these three operations makes IDEA cryptanalysis difficult compared to DES, which is based solely on the operation of exclusive OR, and also makes it possible to abandon the use of S-blocks and replacement tables. IDEA is a modification of the Feistel network.

Phelix

A high-speed stream cipher using a one-time message authentication code. The cipher was presented at the eSTREAM competition in 2004. The authors are Bruce Schneier, Doug Whiting, Stephen Lux and Frederick Muller. The algorithm contains the operations of addition modulo 232, addition modulo 2 and cyclic shift; Phelix uses a 256-bit key and a 128-bit time stamp on the time stamp (English). Some cryptographers expressed concerns about the possibility of obtaining a secret key if the cipher was used incorrectly.
The Helix cipher, built on the simplest operations, became the forerunner to Phelix, but it was hacked. The enhanced Helix was named Phelix, but it was also rejected at the eCrypt competition. The reason for the refusal was controversial — the attacks were based on the selection of the timestamp, which was a weak point of other ciphers, but the developers stated that their cipher was resistant to this kind of attack. It turned out that the cipher is cracked by differential-linear cryptanalysis, although this does not threaten the strength of the cipher in other conditions. As a result, Phelix was not allowed to the third round of the contest, for a certain arrogance and carelessness of the authors. In addition to all this, a number of theoretical works appeared in which it was stated that mixing the operations of add-xor-shift does not give the necessary non-linearity, but in practice there were no hacks.Now the design of Phelix is ​​offered by the authors for use in Skein and Threefish.

The authors report that Phelix should not be used until it has received additional cryptanalysis.

Hongjun Wu and Bart Prenil, the authors of the differential attack, express concern that each open-text word affects the keystream, bypassing sufficient confusion and diffusion layers. They argue that this is an inherent flaw in the structure of Helix and Phelix. The authors conclude that Phelix is ​​unsafe.

Feal

Block cipher developed by Akihiro Shimizu (English Akihiro Shimizu) and Shoji Miyaguchi (English Shoji Miyaguchi) - employees of the company NTT.

It uses a 64-bit block and a 64-bit key. His idea is to create an algorithm like DES, but with a stronger stage function. Using fewer steps, this algorithm could work faster. In addition, unlike DES, the FEAL function does not use S-boxes for the stage, so the implementation of the algorithm does not require additional memory to store replacement tables.

Published in 1987 by Akihiro Shimizu and Shoji Miyaguchi, the FEAL block cipher was designed to increase the encryption speed without sacrificing the cipher reliability compared to DES. Initially, the algorithm used 64-bit blocks, a 64-bit key, and 4 encryption rounds. However, already in 1988, the work of Bert den Boer (Eng. Bert Den-Boer) was published, proving the sufficiency of possession of 10,000 ciphertexts for conducting a successful attack based on a chosen plaintext. One of the first to be applied to the FEAL cipher was linear cryptanalysis. Including in 1992, Mitsuru Matsui and Atsuhiro Yamagishi proved that it is enough to learn 5 ciphertexts to conduct a successful attack.
To combat the discovered vulnerabilities, the creators doubled the number of encryption rounds by publishing the FEAL-8 standard. However, already in 1990, Henry Gilbert (English Henri Gilbert) vulnerability and this cipher before the attack based on the selected plaintext. Further, in 1992, Mitsuru Matsui and Atsuhiro Yamagishi (Mitsuru Matsui and Atsuhiro Yamagishi) described an attack based on open texts.

Due to the large number of successful attacks, the developers decided to further complicate the cipher. Namely, FEAL-N was introduced in 1990, where N is an arbitrary even number of encryption rounds, and represented by FEAL-NX, where X (from extended) means the use of an encryption key extended to 128 bits. However, this innovation has helped only partially. In 1991, Eli Biham and Adi Shamir (Eli Biham and Adi Shamir), using the methods of differential cryptanalysis, showed the possibility of breaking the cipher faster than brute force.

Nevertheless, due to the intensity of the research of the encryption algorithm by the community, the limits of the cipher's vulnerability to linear and differential crypttoanalysis were proved. Shikho Morai, Kazumaro Aoki and Kazuo Ohta (Shiho Moriai, Kazumaro Aoki, and Kazuo Ohta), and in Kazumaro Aoki, Kunio Kobayashi and Shiho Morai (Kazumaro Aoki) and Kazumaro Aoki, showed stability of the algorithm with a number of rounds greater than 26 to linear cryptanalysis. Kobayashi, and Shiho Moriai) proved the impossibility of applying differential cryptanalysis to an algorithm using more than 32 rounds of encryption.

Due to the fact that the FEAL cipher was developed quite early, it served as an excellent training facility for cryptologists from all over the world.

In addition, his example opened linear cryptanalysis. Mitsuru Matsui, the inventor of linear cryptanalysis, in his first work on this topic considered just FEAL and DES.

Dual-key spacecraft

RSA

RSA is an abbreviation for the surnames Rivest, Shamir, and Adleman, a public-key cryptographic algorithm based on the computational complexity of the problem of factoring large integers. Described in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman of the Massachusetts Institute of Technology.

RSA cryptosystem became the first system, suitable for both encryption and digital signature. The algorithm is used in a large number of cryptographic applications, including PGP, S / MIME, TLS / SSL, IPSEC / IKE, and others.The Rivest-Shamir-Adleman (RSA) algorithm is one of the most popular and secure public key encryption methods. The algorithm is based on the fact that there is no effective way to account for very large (100-200 digits) numbers.

RSA keys are generated as follows:

1. Two different random primes are chosen. $$$p$ and $$$q$ (, 1024 ).
2. $$$n=p*q$ , .
3. :
   $$$φ(n) = (p-1)*(q-1)$
4. $$$e$ ( $$$1< e < φ(n)$ ), φ(n) $$$φ(n)$ . $$$e$ , , , 17, 257 65537.
   
   
   • Number $$$e$ (. public exponent)
   • , , $$$e$ .
   • $$$e$ , 3, RSA.
   
   
5. $$$d$ , $$$e$ $$$φ(n)$ , , : $$$d\cdot e\equiv 1{\pmod {\varphi (n)}}.$
   . , .
6. { $$$e, n$ } RSA.
7. { $$$d, n$ } RSA .

RSA security depends on the computational complexity of factoring large integers. As the computing power increases and more efficient factoring algorithms are discovered, the ability to increase the number and large numbers also increases. Encryption is directly tied to the key size, and doubling the key length provides an exponential increase in strength, although it reduces performance.

DSA

DSA is a cryptographic algorithm using the public key to create an electronic signature, but not for encryption (unlike RSA and El-Gamal scheme). The signature is created secretly, but can be publicly verified. This means that only one subject can create a message signature, but anyone can verify its correctness. The algorithm is based on the computational complexity of taking logarithms in finite fields.

The algorithm was proposed by the National Institute of Standards and Technology (USA) in August 1991 and is patented; NIST made this patent available for use without license fees. DSA is part of DSS, first published December 15, 1998. The standard has been updated several times, the latest version of FIPS-186-4.

DSA includes two algorithms (S, V): to create a message signature (S) and to verify it (V).

Both algorithms first compute a message hash using a cryptographic hash function. Algorithm S uses the hash and the secret key to create a signature, algorithm V uses the message hash, the signature and the public key to verify the signature.

In fact, it’s not the message (of arbitrary length) that is signed, but its hash (160-256 bits).

The message signature is performed according to the following algorithm:

1. Random number selection $$$k \in (0;q)$
2. Calculation $$$r=(g^k\mod p)\mod q$
3. Calculation $$$s=(k^{-1}(H(m)+x\cdot r))\mod q$
4. Choose another $$$k$ if it turned out that $$$r=0$ or $$$s=0$
5. Signature is a pair of numbers $$$(r, s)$

Signature verification The signature

verification is performed by the algorithm:

1. Calculation $$$w=s^{-1} \mod q$
2. Calculation $$$u_1 = (H(m)\cdot w)\mod q$
3. Calculation $$$u_2 = (r\cdot w)\mod q$
4. Calculation $$$v = ((g^{u_1}\cdot y^{u_2})\mod p) \mod q$
5. The signature is valid if $$$v = r$

Elgamal

The asymmetric algorithm proposed by El Gamal in 1985 (T. ElGamal) is universal. It can be used to solve all three main tasks: to encrypt data, to generate a digital signature and to agree on a common key. In addition, modifications are possible for password verification schemes, proof of message identity, and other options. The security of this algorithm, as well as the Diffie-Hellman algorithm, is based on the difficulty of computing discrete logarithms. This algorithm actually uses the Diffie-Hellman scheme to generate a shared secret key for subscribers sending each other a message, and then the message is encrypted by multiplying it with that key.
Both in the case of encryption and in the case of digital signature generation, each user needs to generate a pair of keys. For this, as in the Diffie-Hellman scheme, some large prime number is chosen.$$ and number $$, such that different degrees of A are different numbers by module $$.Numbers P and A can be transmitted in open form and be common to all subscribers on the network.

Then each group subscriber chooses his secret number.$$$i, 1 < i < -1$$ , and calculates the corresponding open number $$$Y_i : Y_i = A^{X_i}\: mod \: P$ . Thus, each user can generate a private key. $$$i$ and public key $$$Yi$ .

Rabin

This algorithm was published in January 1979 by Michael O. Rabin. Rabin's cryptosystem was the first asymmetric cryptosystem in which the recovery of the entire plaintext from the ciphertext could be proved as strongly as factoring.

Key generation:


Choose two large different numbers p and q. Can choose$$$p \equiv q \equiv 3 \ mod \ 4$to simplify the calculation of square roots modulo p and q (see below). But the scheme works with any strokes.

Let$$$n =\ p \ *\ q$ , Then n is the public key. Prime numbers $$$p$ and $$$q$are private key.

Only public key is required for message encryption.$$$n$ . Factors are needed to decrypt the cipher text. $$$p$ and $$$q$ , $$$n$ .

Key generation

1. two random numbers p and q are selected, taking into account the following requirements:
2. numbers must be large (see bit depth);
3. numbers should be simple;
4. the condition must be met: $$$p ≡ q ≡ 3 mod 4$ .

Fulfillment of these requirements greatly accelerates the procedure of extracting roots modulo p and q;
the number is calculated$$$n = p * q$ ;

1. n is the public key;
2. the numbers p and q are closed.

Encryption

The original message m (text) is encrypted using the public key - the number n according to the following formula:$$$c = m² \ mod \ n.$
By using the modulo multiplication, Rabin’s system’s encryption speed is greater than the RSA encryption rate, even if in the latter case a small exponent value is chosen.

Decryption
To decrypt a message you need a private key - the numbers p and q. The decryption process is as follows:

1. First, using the Euclidean algorithm , from the equation$$$y_{p}\cdot p+y_{q}\cdot q=1$ find numbers $$$y_{p}$ and $$$y_{q}$ ;
2. further, using the Chinese theorem on residues , calculate four numbers:
   
   $$${\begin{matrix}r&=&(y_{p}\cdot p\cdot m_{q}+y_{q}\cdot q\cdot m_{p})\,{\bmod {\,}}n\\-r&=&n-r\\s&=&(y_{p}\cdot p\cdot m_{q}-y_{q}\cdot q\cdot m_{p})\,{\bmod {\,}}n\\-s&=&n-s\end{matrix}}$
   

One of these numbers is true plaintext m.

PS If anyone is interested, then almost all the algorithms presented in this article have archives with the implementation in C, C ++ or Assembler (in one of the languages), respectively, the implementation is not mine, I will say more to use them is unlikely to work although who knows.

PPS I had an idea to also make a comparison table, but first I would like to know by which parameters you would like to see a comparison.

PPPS For the article contest “Netology”, Link to the site , Link to the blog .